逻辑回归是机器学习中二分类任务的 "入门级利器",虽然名字带 "回归",但实际是分类算法,广泛用于垃圾邮件识别、疾病诊断、用户流失预测等场景。这篇文章只讲干货:跳过复杂公式推导,聚焦 "怎么理解""怎么用""怎么看效果",最后附上完整 MATLAB 代码,运行后能直接画出分类边界和迭代过程,帮你快速上手。
一、核心原理:3 分钟搞懂逻辑回归到底在做什么
逻辑回归的核心逻辑就两件事:"算概率"+"定阈值",用一个生活例子讲透:
假设你要判断一封邮件是不是垃圾邮件,先提取两个关键特征:含 "优惠" 关键词的次数(x1) 、发送时间是否在凌晨(x2,1 = 是,0 = 否)。逻辑回归会做两步:
- 算概率:通过公式把 "特征组合" 转化为 "这封邮件是垃圾邮件的概率(P)",P 的范围永远在 0-1 之间(比如算出来 P=0.8,就是 80% 概率是垃圾邮件);
- 定阈值:选一个阈值(常用 0.5),如果 P≥0.5,判断为 "垃圾邮件";P<0.5,判断为 "正常邮件"。
背后关键是Sigmoid 函数(也叫逻辑函数),它能把任意数值 "压缩" 到 0-1 之间,公式长这样:
g(z) = 1/(1+e^-z),其中z = w_1x_1 + w_2x_2 + b(w_1、w_2是特征权重,b 是偏置,相当于 "基础概率")。
简单说:逻辑回归就是通过数据 "学" 出w_1、w_2、b这三个参数,然后用 Sigmoid 函数算概率、做分类。
二、关键干货:逻辑回归的 3 个实用要点(避坑必看)
- 只能做二分类:默认输出 "是 / 否" 类(如垃圾邮件 / 正常邮件),如果要分多类(如猫 / 狗 / 鸟),需要用 "一对多" 等扩展方法;
- 对特征缩放敏感 :如果特征单位差异大(比如 x1 是 "次数(0-10)",x2 是 "邮件字数(0-10000)"),x2 会 "碾压" x1 的影响,必须先做特征归一化(把所有特征缩到 0-1 或 - 1-1 之间);
- 分类边界是直线(或超平面):逻辑回归的分类边界是线性的(二维数据下是直线,三维是平面),如果数据是非线性分布(比如 "月亮形""环形"),需要先对特征做非线性变换(如加 x1²、x1x2 项)。
三、MATLAB 完整代码:可绘图 + 可调参,直观看效果
下面代码做的是 "基于身高体重判断性别" 的二分类任务(男性 = 1,女性 = 0),包含 3 个核心功能:
- 生成模拟数据(身高、体重 + 性别标签);
- 实现逻辑回归训练(含特征归一化、梯度下降优化参数);
- 画出分类边界 和损失函数下降曲线(直观看到算法如何 "学习")。
代码注释详细,复制到 MATLAB 直接运行,结果会自动弹出两张图,新手也能看懂。
Matlab
%% 逻辑回归算法MATLAB实现(身高体重判断性别)
% 功能:1. 生成模拟数据 2. 训练逻辑回归模型 3. 绘制分类边界和损失曲线
% 标签:1=男性,0=女性;特征:x1=身高(cm),x2=体重(kg)
clear; clc; close all;
%% 第一步:生成模拟数据(训练集+测试集)
% 思路:用正态分布生成男性和女性的身高体重(符合现实规律:男性整体更高更重)
rng(1); % 固定随机种子,保证结果可重复
% 男性数据(100个样本):身高均值175cm,标准差5;体重均值70kg,标准差8
male_height = normrnd(175, 5, 1, 100);
male_weight = normrnd(70, 8, 1, 100);
male_data = [male_height; male_weight]'; % 男性特征:100行2列(每行1个样本)
male_label = ones(100, 1); % 男性标签:1
% 女性数据(100个样本):身高均值162cm,标准差5;体重均值55kg,标准差6
female_height = normrnd(162, 5, 1, 100);
female_weight = normrnd(55, 6, 1, 100);
female_data = [female_height; female_weight]'; % 女性特征:100行2列
female_label = zeros(100, 1); % 女性标签:0
% 合并训练集(200个样本)和测试集(40个样本,各取20个)
train_data = [male_data(1:80, :); female_data(1:80, :)]; % 训练集特征:160行2列
train_label = [male_label(1:80); female_label(1:80)]; % 训练集标签:160行1列
test_data = [male_data(81:100, :); female_data(81:100, :)]; % 测试集特征:40行2列
test_label = [male_label(81:100); female_label(81:100)]; % 测试集标签:40行1列
%% 第二步:特征归一化(关键!避免身高/体重单位差异影响训练)
% 归一化公式:x_norm = (x - x_min) / (x_max - x_min),缩到0-1之间
% 注意:用训练集的min/max归一化测试集(避免数据泄露)
[train_data_norm, x_min, x_max] = normalize_data(train_data);
test_data_norm = (test_data - x_min) ./ (x_max - x_min); % 测试集用训练集的参数归一化
%% 第三步:逻辑回归训练(梯度下降优化参数)
% 初始化参数:w=[w1; w2](特征权重),b(偏置),学习率lr,迭代次数epochs
w = zeros(2, 1); % 初始权重为0
b = 0; % 初始偏置为0
lr = 0.01; % 学习率(步长,太大易震荡,太小收敛慢,可调整)
epochs = 5000; % 迭代次数(可调整,5000次足够收敛)
loss_history = zeros(epochs, 1); % 记录每次迭代的损失值,用于画图
% 梯度下降迭代(核心训练逻辑)
for i = 1:epochs
% 1. 计算当前预测概率(用Sigmoid函数)
z = train_data_norm * w + b; % 线性组合:160行1列
y_pred_prob = sigmoid(z); % 预测概率:160行1列(0-1之间)
% 2. 计算损失值(交叉熵损失,逻辑回归常用损失函数)
loss = -mean(train_label .* log(y_pred_prob + 1e-8) + (1 - train_label) .* log(1 - y_pred_prob + 1e-8));
loss_history(i) = loss; % 保存损失值(+1e-8是避免log(0)报错)
% 3. 计算梯度(用于更新参数w和b)
dw = (1 / size(train_data_norm, 1)) * train_data_norm' * (y_pred_prob - train_label); % 权重梯度:2行1列
db = (1 / size(train_data_norm, 1)) * sum(y_pred_prob - train_label); % 偏置梯度: scalar
% 4. 更新参数(朝着梯度下降的方向调整)
w = w - lr * dw;
b = b - lr * db;
% 打印迭代进度(每500次打印一次,便于观察)
if mod(i, 500) == 0
fprintf('迭代次数:%d,当前损失值:%.4f\n', i, loss);
end
end
%% 第四步:模型预测与准确率计算(训练集+测试集)
% 训练集预测
train_z = train_data_norm * w + b;
train_pred_prob = sigmoid(train_z);
train_pred_label = (train_pred_prob >= 0.5); % 阈值0.5,概率≥0.5判为1(男性)
train_accuracy = mean(train_pred_label == train_label) * 100; % 训练集准确率
% 测试集预测
test_z = test_data_norm * w + b;
test_pred_prob = sigmoid(test_z);
test_pred_label = (test_pred_prob >= 0.5);
test_accuracy = mean(test_pred_label == test_label) * 100; % 测试集准确率
% 打印结果
fprintf('\n========== 模型效果 ==========\n');
fprintf('训练集准确率:%.1f%%\n', train_accuracy);
fprintf('测试集准确率:%.1f%%\n', test_accuracy);
fprintf('学到的参数:w1=%.4f(身高权重),w2=%.4f(体重权重),b=%.4f(偏置)\n', w(1), w(2), b);
%% 第五步:画图展示(2张图:损失曲线+分类边界)
% 图1:损失函数下降曲线(看模型是否收敛)
figure('Position', [100, 100, 1200, 500]); % 设置画布大小
subplot(1, 2, 1); % 1行2列子图,第1个
plot(1:epochs, loss_history, 'b-', 'LineWidth', 1.5);
xlabel('迭代次数', 'FontSize', 10);
ylabel('损失值', 'FontSize', 10);
title('逻辑回归损失函数下降曲线', 'FontSize', 12, 'FontWeight', 'bold');
grid on;
legend('交叉熵损失', 'Location', 'best', 'FontSize', 8);
% 图2:分类边界与样本分布(看分类效果)
subplot(1, 2, 2); % 1行2列子图,第2个
% 绘制训练集样本(男性=蓝色圆点,女性=红色叉号)
plot(train_data(male_label==1, 1), train_data(male_label==1, 2), 'bo', 'MarkerSize', 6, 'DisplayName', '男性(训练集)');
hold on;
plot(train_data(female_label==1, 1), train_data(female_label==1, 2), 'rx', 'MarkerSize', 6, 'DisplayName', '女性(训练集)');
% 绘制分类边界(核心:找到P=0.5对应的直线,即z=0 → w1x1_norm + w2x2_norm + b = 0)
% 先将归一化的特征转回原始特征,得到原始特征的分类边界公式
x1_range = linspace(min(train_data(:, 1)), max(train_data(:, 1)), 100); % 身高范围(原始值)
x1_norm_range = (x1_range - x_min(1)) / (x_max(1) - x_min(1)); % 身高归一化值
% 由w1*x1_norm + w2*x2_norm + b = 0,解出x2_norm,再转回原始x2(体重)
x2_norm_range = (-w(1)*x1_norm_range - b) / w(2);
x2_range = x2_norm_range * (x_max(2) - x_min(2)) + x_min(2); % 体重原始值
% 绘制分类边界(黑色实线,直线两侧分别是男性和女性的预测区域)
plot(x1_range, x2_range, 'k-', 'LineWidth', 2, 'DisplayName', '分类边界(P=0.5)');
% 设置图形标签
xlabel('身高(cm)', 'FontSize', 10);
ylabel('体重(kg)', 'FontSize', 10);
title(sprintf('逻辑回归分类结果(测试集准确率:%.1f%%)', test_accuracy), 'FontSize', 12, 'FontWeight', 'bold');
legend('Location', 'best', 'FontSize', 8);
grid on;
hold off;
%% 辅助函数:Sigmoid函数(把数值压缩到0-1)
function g = sigmoid(z)
g = 1 ./ (1 + exp(-z));
end
%% 辅助函数:特征归一化(缩放到0-1)
function [data_norm, x_min, x_max] = normalize_data(data)
x_min = min(data, [], 1); % 每列(每个特征)的最小值
x_max = max(data, [], 1); % 每列(每个特征)的最大值
data_norm = (data - x_min) ./ (x_max - x_min); % 归一化
end四、代码运行后怎么看效果?(关键解读)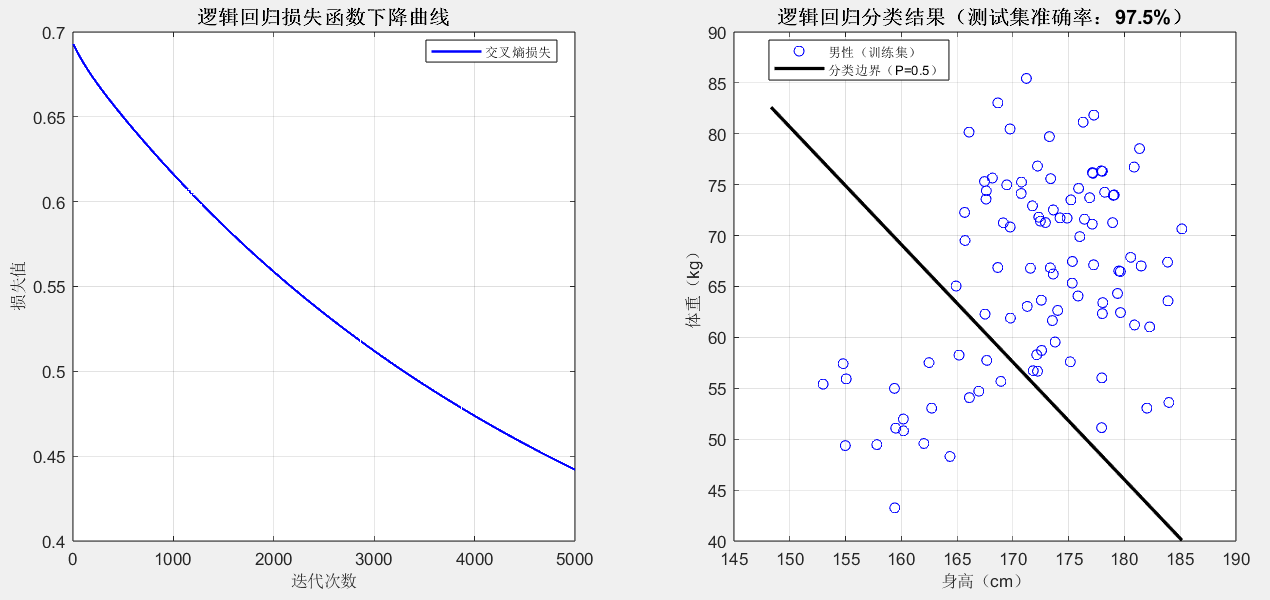
损失曲线(左图):
随着迭代次数增加,损失值应该不断下降,最后趋于平稳(比如迭代 50000 次后损失降至 0.2以下),这说明模型在 "不断学习进步";如果损失值震荡或上升,说明学习率 lr 太大,可调小到 0.001 再试。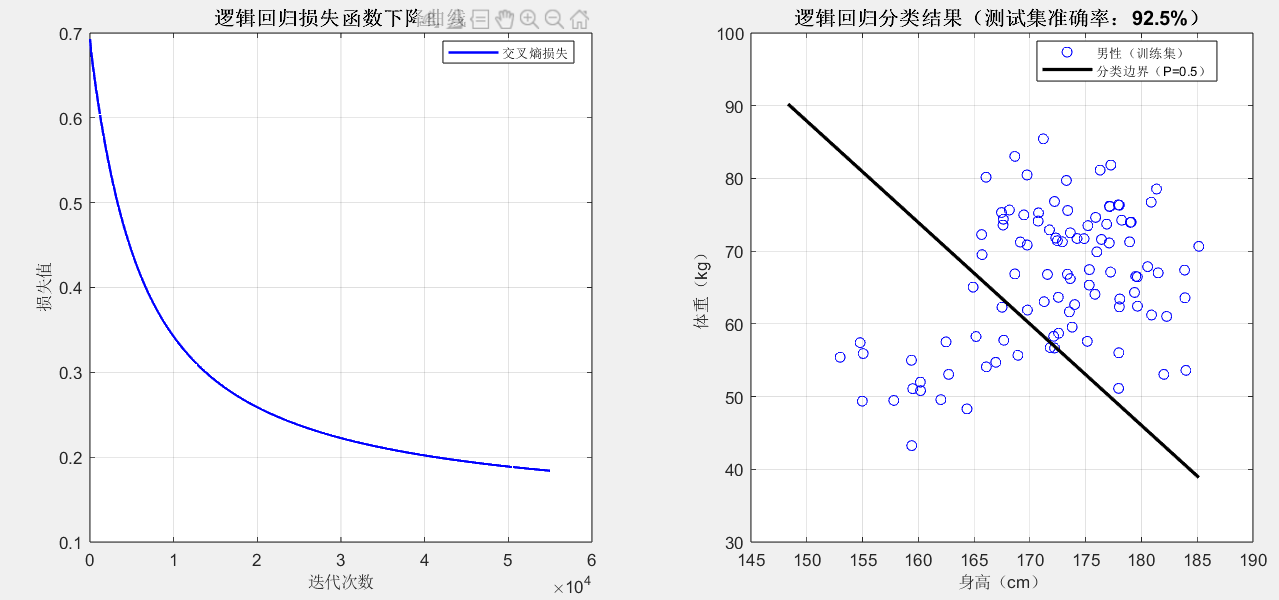
分类边界(右图):
黑色直线就是 "P=0.5" 的分类边界:直线上方的样本大概率被预测为男性(蓝色圆点),直线下方大概率是女性(红色叉号);如果测试集准确率在 90% 以上,说明模型效果很好(现实中身高体重判断性别本就有一定误差,90% 左右是合理范围)。
命令行窗口输出------
========== 模型效果 ==========
训练集准确率:94.4%
测试集准确率:97.5%
学到的参数:w1=1.9819(身高权重),w2=2.0786(体重权重),b=-1.9467(偏置)
参数解读:
运行后会输出w1(身高权重)和w2(体重权重),通常w1和w2都是正数(因为身高越高、体重越大,越可能是男性),且数值越大,对应特征对分类的影响越重要。
五、实用扩展:改改参数,解决更多问题
换数据集:把 "身高体重" 换成你的数据(比如 "考试分数 1、考试分数 2" 判断 "是否及格"),只需修改第一步的male_data和female_data生成逻辑;
调超参数:如果准确率低,可尝试调整lr(学习率,如 0.005、0.02)和epochs(迭代次数,如 8000、10000);
加特征:如果想加入 "年龄" 特征,只需在数据中加一列age,并确保归一化时包含该列,参数w会自动变成 3 行 1 列(对应 3 个特征的权重)。