leetcode LCR 170.交易逆序对的总数

一、问题描述

二、解题思路

整体思路

可以借鉴**归并排序(递归)**的求解过程。假设数组如图所示，总过程为：

(1)首先找到中间位置mid;

(2)在[left,mid]区间内统计逆序对的数量+排序;

(3)再在[mid+1,right]区间内统计逆序对的数量+排序;

(4)最后再一左一右统计逆序对的数量+排序;

(5)将三个数量累加，即为所求。

具体思路

(1)首先，考虑递归出口，如果left>=right，即区间内只有1个数或者没有数，此时逆序对的数量为0，return0；

(2)寻找中间位置，执行左区间寻找+排序、右区间寻找+排序，代码如下：

//1.寻找中间位置

int mid=left+(right-left)/2;

//2.左区间寻找+排序、右区间寻找+排序

ret+=mergeSort(nums,left,mid);

ret+=mergeSort(nums,mid+1,right);

(3)由于递归需要保证子问题一样，所以我们在一左一右统计逆序对的数量后，也进行排序处理。我们处理的总策略是寻找左边更大的数的个数，处理过程如下，此时的数组如图。当cur1<=mid且cur2<=right时进行归并处理，并进行逆序对数量统计：

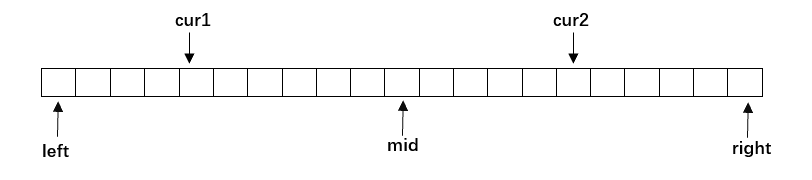
<1>当nums[cur1]<=nums[cur2]时，执行tmp[i++]=nums[cur1++]；

<2>当nums[cur1]>nums[cur2]时，此时[cur1,mid]区间内的数均比nums[cur2]大，所以ret+=mid-cur1+1，tmp[i++]=nums[cur2++]；

(4)循环结束后，将归并排序的过程完成：

//4.处理没有排序完的数字

while(cur1<=mid) tmp[i++]=nums[cur1++];

while(cur2<=right) tmp[i++]=nums[cur2++];

(5)排序完成后用排序完的辅助数组tmp覆盖原本的数组nums：

//5.还原nums数组

for(int i=left;i<=right;i++)

nums[i]=tmp[i-left];

(6)最后返回ret；

三、代码实现

时间复杂度：T(n)=O(nlogn)

空间复杂度：S(n)=O(n)

cpp 复制代码

class Solution {
    vector<int> tmp;
public:
    int reversePairs(vector<int>& nums) {
       //结合归并排序
       tmp.resize(nums.size());
       return mergeSort(nums,0,nums.size()-1);
    }

    int mergeSort(vector<int>& nums,int left,int right){
        //递归出口
        if(left>=right) return 0;

        int ret=0;
        //1.寻找中间位置
        int mid=left+(right-left)/2;
        //2.左区间寻找+排序、右区间寻找+排序
        ret+=mergeSort(nums,left,mid);
        ret+=mergeSort(nums,mid+1,right);
        //3.一左一右寻找+排序
        int cur1=left,cur2=mid+1,i=0;
        while(cur1<=mid&&cur2<=right){
            if(nums[cur1]<=nums[cur2]){
                tmp[i++]=nums[cur1++];
            }
            else{
                ret+=mid-cur1+1;
                tmp[i++]=nums[cur2++];
            }
        }
        //4.处理没有排序完的数字
        while(cur1<=mid) tmp[i++]=nums[cur1++];
        while(cur2<=right) tmp[i++]=nums[cur2++];
        //5.还原nums数组
        for(int i=left;i<=right;i++)
            nums[i]=tmp[i-left];
        //6.返回ret
        return ret;
    }
};