

文章目录
- 前言:
-
- [《算法磨剑: 用C++思考的艺术》 专栏](#《算法磨剑: 用C++思考的艺术》 专栏)
- [《C++:从代码到机器》 专栏](#《C++:从代码到机器》 专栏)
- [《Linux系统探幽:从入门到内核》 专栏](#《Linux系统探幽:从入门到内核》 专栏)
- 正文:
-
- [[B3644 【模板】拓扑排序 / 家谱树](https://www.luogu.com.cn/problem/B3644)](#B3644 【模板】拓扑排序 / 家谱树)
- [[P2712 摄像头](https://www.luogu.com.cn/problem/P2712)](#P2712 摄像头)
- [[P4017 最大食物链计数](https://www.luogu.com.cn/problem/P4017)](#P4017 最大食物链计数)
- [3 :[P1113 杂务](https://www.luogu.com.cn/problem/P1113)](#3 :P1113 杂务)
- 结语:
前言:
《算法磨剑: 用C++思考的艺术》 专栏
专注用C++破解算法面试真题,详解LeetCode热题,构建算法思维,从容应对技术挑战。
👉 点击关注专栏
《C++:从代码到机器》 专栏
深入探索C++从语法特性至底层原理的奥秘,构建坚实而深入的系统编程知识体系。
👉 点击关注专栏
《Linux系统探幽:从入门到内核》 专栏
深入Linux操作系统腹地,从命令、脚本到系统编程,探索Linux的运作奥秘。
👉 点击关注专栏
作者:孤廖
学习方向 :C++/Linux/算法
人生格言:折而不挠,中不为下
正文:
B3644 【模板】拓扑排序 / 家谱树
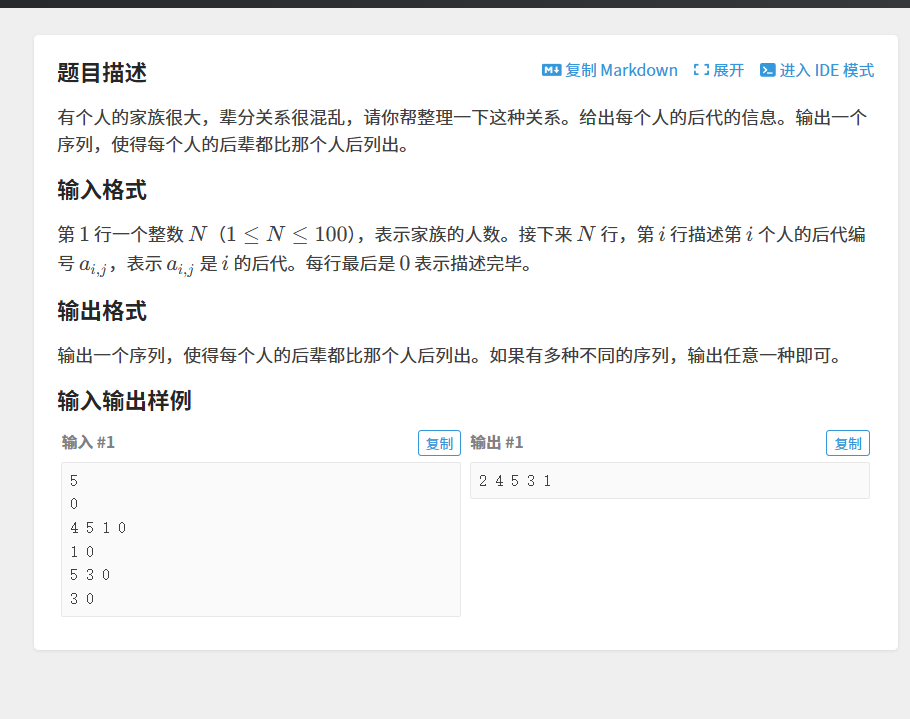
【解法】
【参考代码】
#define _CRT_SECURE_NO_WARNINGS
//B3644 【模板】拓扑排序 / 家谱树
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 110;
vector<int> edges[N];//edges[i]:表示i节点的孩子 邻接表(孩子表示法)
int d[N];//d[i]:i节点的入度数
int n;
int main()
{
cin >> n;
//处理图的信息
for (int i = 1; i <= n; i++)
{
int j;
while (cin >> j, j)
{
edges[i].push_back(j);
d[j]++;//更新每个节点的入度数
}
}
//拓扑排序
queue<int> q;
//先把入度数为0 的点 加入队列
for (int i = 1; i <= n; i++) if (d[i] == 0) q.push(i);
while (q.size())
{
int a = q.front(); q.pop();///出队
cout << a << " ";
//更新入度数
for (auto& e : edges[a])
{
d[e]--;
if (d[e] == 0) q.push(e);
}
}
return 0;
}P2712 摄像头

【解法】:
拓扑排序判断是否有环。
直接跑⼀遍拓扑排序,然后统计⼀下有多少摄像头没有出队。那么这些没有出队的摄像头就是环⾥⾯的元素。
注意:
• 有些位置可能没有摄像头,需要判断⼀下。
【参考代码】
#define _CRT_SECURE_NO_WARNINGS
//P2712 摄像头
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 510;
vector<int> edges[N];//edges[i]:表示i 的边的信息即i指向的孩子
int n;//摄像头的个数
int d[N];//d[i]:表示节点i的入度数
bool st[N];//st[i]:表示i位置是否有摄像头
int main()
{
cin >> n;
//输入摄像头的信息 即图的信息
for (int i = 1; i <= n; i++)
{
int x, m, y;
cin >> x >> m;
st[x] = true;
while (m--)
{
cin >> y;
edges[x].push_back(y);
//统计节点入度数
d[y]++;
}
}
//拓扑排序
queue<int> q;
//将入度数 为0的摄像头入队
for (int i = 0; i <= 500; i++)
{
if (d[i] == 0 && st[i] ) q.push(i);
}
while (q.size())
{
//将入度数为0的摄像头 出队
int a = q.front(); q.pop();
//更新与a摄像头相关的摄像头的入度数
for (auto& e : edges[a])
{
d[e]--;
if (st[e] && d[e] == 0) q.push(e);
}
}
//遍历所有位置找到是否还有没有砸坏的摄像头
int ret = 0;//还没砸掉的摄像头数量
for (int i = 0; i <= 500; i++)
{
if (st[i] && d[i]) ret++;
}
if (ret == 0) cout << "YES " << endl;
else cout << ret << endl;
return 0;
}P4017 最大食物链计数

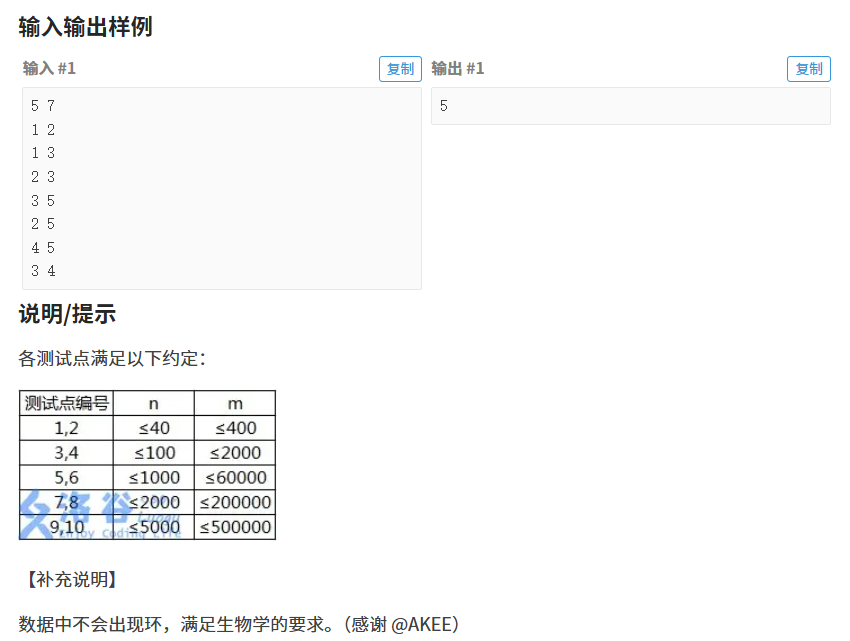
【解法】
注意审题!题⽬问的是⼀共有多少条路径!
拓扑排序的过程中,进⾏动态规划。
对于每⼀个节点 ,通过它的路径为:前驱所有结点的路径总数之和。因此,可以在拓扑排序的过程中,维护从起点开始到达每⼀个节点的路径总数。
【参考代码】
#define _CRT_SECURE_NO_WARNINGS
//P4017 最大食物链计数
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 5010,M=5e5+10,MOD= 80112002;
int f[N];//f[i]:表示从生产者到i种生物的最大食物链条数
vector<int> edges[M];//边数
int in[N];//in[i]:表示:i种能被多少种生物吃掉即入度数
int out[N];//out[i]:表示:i种生物能吃多少种生物即出度数
int n, m;//物种的个数 和食物链的条数
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
int x, y;//x->y
cin >> x >> y;
//统计边的信息,和每个节点 的出入度情况
edges[x]. push_back(y);
in[y]++;
out[x]++;
}
//dp+拓扑排序
//初始化 初始化生产者的最大食物链条数 即为1
queue<int> q;
for (int i = 1; i <= n; i++)
{
if (in[i] == 0)
{
f[i] = 1;//初始化
q.push(i);//生产者入队
}
}
while (q.size())
{
int a = q.front(); q.pop();//入度数为0的生物出队
//更新a的捕食者的最大生物链条数
for (auto& e : edges[a])
{
//a->e
in[e]--;
f[e] = (f[e] + f[a]) % MOD;//模加模防止溢出
if (in[e] == 0) q.push(e);
}
}
//统计不同食物网最大的食物链条数总和
int ret = 0;//结果
for (int i = 1; i <= n; i++)
{
if (out[i] == 0) ret = (ret + f[i]) % MOD;//模加模防止溢出
}
//输出结果
cout << ret << endl;
return 0;
}3 :P1113 杂务

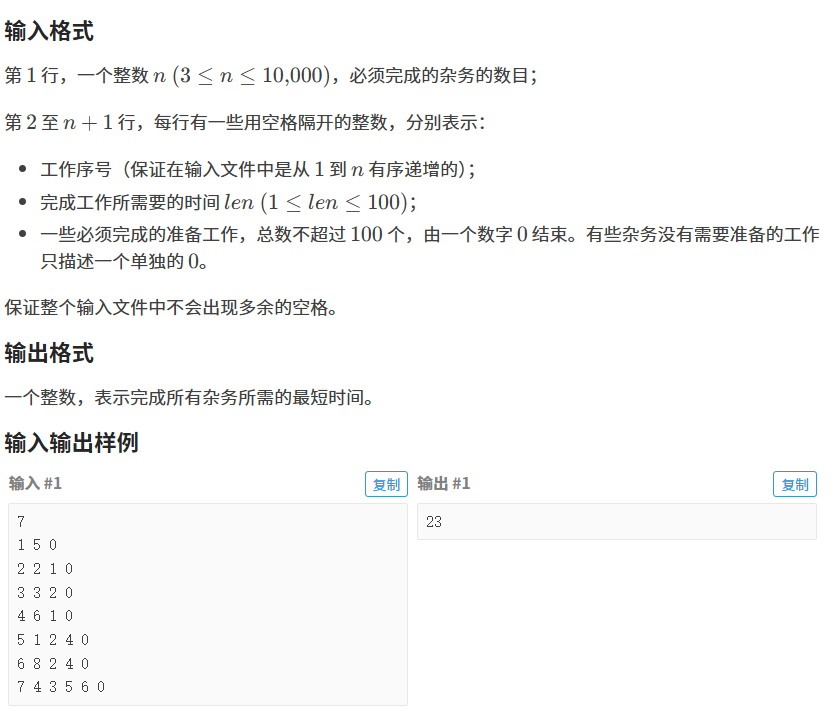
【解法】
拓扑排序的过程中,进⾏动态规划。
对于每⼀个事件 ,完成它的最⼩时间为:完成前驱所有事件的最⼩时间中的最⼤值 + 当前事件的完
成时间。因此,可以在拓扑排序的过程中,维护每⼀个事件完成的最⼩时间,然后更新当前事件的最⼩时间。
第一种初始化下:
#define _CRT_SECURE_NO_WARNINGS
//P1113 杂务
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 1e4 + 10;
int f[N];//f[i]:i杂物完成所需的最小时间
int n;//n 个杂物
vector<int> edges[N];//edges[i]:杂物i完成后能完成的杂物
int len[N];//len[i]:杂物i完成需要的时间
int in[N];//in[i]:杂物i的入度即做杂物i前 需要完成的其他杂物个数
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
int b = 0, a = 0;//当前杂物b 作杂务b前需要完成的杂物a
cin >> b >> len[b];
while (cin >> a, a)
{
edges[a].push_back(b);
in[b]++;
}
}
//dp +拓扑排序
//默认初始化
int ret = 0;//结果
queue<int> q;
for (int i = 1; i <= n; i++)
{
if (in[i] == 0) q.push(i);
}
while (q.size())
{
int pre = q.front(); q.pop();//出队
f[pre] += len[pre];
ret = max(ret, f[pre]);
//更新后续要完成杂物的最小时间
for (auto& e : edges[pre])
{
in[e]--;
f[e] = max(f[e], f[pre]);
if (in[e] == 0) q.push(e);
}
}
//输出结果
cout << ret << endl;
return 0;
}第二种初始化下
#define _CRT_SECURE_NO_WARNINGS
//P1113 杂务
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 1e4 + 10;
int f[N];//f[i]:i杂物完成所需的最小时间
int n;//n 个杂物
vector<int> edges[N];//edges[i]:杂物i完成后能完成的杂物
int len[N];//len[i]:杂物i完成需要的时间
int in[N];//in[i]:杂物i的入度即做杂物i前 需要完成的其他杂物个数
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
int b = 0, a = 0;//当前杂物b 作杂务b前需要完成的杂物a
cin >> b >> len[b];
while (cin >> a, a)
{
edges[a].push_back(b);
in[b]++;
}
}
//dp +拓扑排序
//初始化
int ret = 0;//结果
queue<int> q;
for (int i = 1; i <= n; i++)
{
if (in[i] == 0)
{
q.push(i);
f[i] = len[i];
}
}
while (q.size())
{
int pre = q.front(); q.pop();//出队
//更新后续要完成杂物的最小时间
ret = max(ret, f[pre]);
for (auto& e : edges[pre])
{
in[e]--;
f[e] = max(f[e], len[e] + f[pre]);
if (in[e] == 0) q.push(e);
}
}
//输出结果
cout << ret << endl;
return 0;
}结语:
这篇拓扑排序专题,我们从四道洛谷题里挖出了算法 "不变的核心" 与 "多变的场景"------B3644 作为模板题,用 C++ 的vector邻接表 +queue搭好了 Kahn 算法的基础框架,让 "入度维护 + 节点遍历" 的逻辑变得直观 ;P2712 摄像头则在模板上加了 "环检测" 的实际需求,靠 "拓扑序列长度与节点数对比" 快速破题,C++ 的st数组又帮我们精准筛选出有摄像头的位置,避免无效计算;P4017 最大食物链计数更巧妙,把拓扑排序和 DP 结合,用f数组同步累加路径数,模运算的细节处理还兼顾了数据溢出问题;而 P1113 杂务则聚焦 "最长路径",两种初始化方式的对比,让我们看清f数组维护 "前置任务最大时间" 的本质,也体会到 C++ 代码实现的灵活性。
其实拓扑排序的魅力,就在于它能把 "依赖关系" 转化为 "可计算的顺序",而 C++ 则是把这种思路落地的关键 ------ 选queue还是priority_queue,用数组还是vector存状态,甚至初始化的时机,都会影响代码的效率与可读性。这也是 "算法磨剑" 的意义:不只是会背模板,更是能根据题目场景,用 C++ 把算法 "磨" 成贴合需求的工具。
如果这篇解析帮你理清了拓扑排序的不同应用场景,或是对 C++ 实现细节有了新理解,不妨点个赞 + 收藏,方便后续复盘;也欢迎在评论区分享你的思考:你解 P2712 时有没有先想到其他判环方法?P1113 的两种初始化方式,你更偏爱哪种逻辑?后续 "算法磨剑:用 C++ 思考的艺术" 专栏还会继续深挖图论、动态规划等算法的实战场景,陪你从 "会用算法" 到 "用好算法",在代码里一步步精进!