DenseNet详解与实现

- [0. 前言](#0. 前言)
- [1. DenseNet 架构](#1. DenseNet 架构)
- - [1.1 DenseNet 原理](#1.1 DenseNet 原理)
  - [1.2 瓶颈层与过渡层](#1.2 瓶颈层与过渡层)
- [2. 构建 DenseNet](#2. 构建 DenseNet)

0. 前言

DenseNet 允许每个卷积直接访问输入和较低层的特征图，从而进一步改进了 ResNet。通过利用瓶颈层 (Bottleneck) 和过渡层 (Transition)，还可以使深度网络中的参数数量保持较低。

1. DenseNet 架构

我们已经学习了ResNet解决深度卷积网络中消失的梯度问题，DenseNet 使用另一种方法来解决梯度消失的问题。

1.1 DenseNet 原理

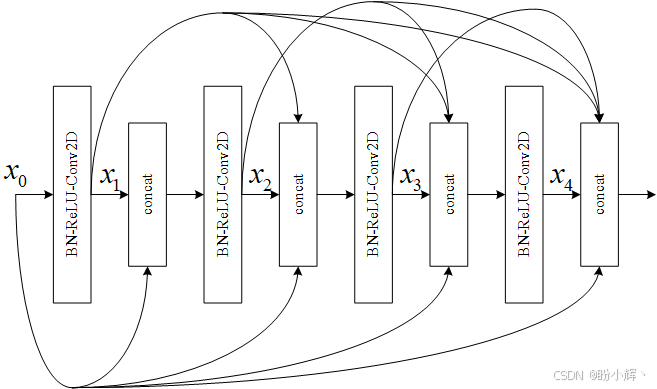
所有先前的特征图都将成为下一层的输入。请注意，第 l l l 层的输入是所有先前特征图的串联。如果用操作 H ( x ) H(x) H(x) 表示 BN-ReLU-Conv2D，则层 l l l 的输出为：
x l = H ( x 0 , x 1 , x 2 , . . . , x l − 1 ) x_l = H (x_0,x_1,x_2,...,x_{l-1}) xl=H(x0,x1,x2,...,xl−1)
Conv2D 使用大小为 3 的卷积核。每层生成的特征图的数量称为增长率 k k k。通常， k = 12 k = 12 k=12。因此，如果特征图 x 0 x_0 x0 的数量为 k 0 k_0 k0，则 4 层密集块末尾的特征图的总数将为 4 k + k 0 4k + k_0 4k+k0。
DenseNet 建议在Dense块之前加上 BN-ReLU-Conv2D，这些特征图的数量是增长率的两倍： k 0 = 2 k k_0 = 2k k0=2k。在密集块的末尾，特征图的总数将为 4 k + 2 k = 6 k 4k + 2k = 6k 4k+2k=6k。

在输出层，DenseNet 建议在带有 softmax 层的 Dense() 之前执行平均池化。如果未使用数据增强，则必须在 Dense 块 Conv2D 之后跟随一个 dropout 层。

1.2 瓶颈层与过渡层

随着网络的深入，将出现两个新问题。首先，由于每一层都增加了 k k k 个特征图，因此层 l l l 的输入数量为 ( l -- 1 ) k + k 0 (l -- 1)k + k_0 (l--1)k+k0。特征图在深层网络中快速增长，从而减慢了计算速度。

其次，与 ResNet 相似，随着网络的不断深入，特征图的大小将减小，从而增加了核的感受野大小。如果 DenseNet 在合并操作中使用串联，则必须协调大小上的差异。

为了防止特征图的数量增加导致计算效率低，DenseNet 引入了瓶颈层。这个想法是，在每次串联之后，现在应用 1 x 1 卷积，其卷积核数量为 4 k 4k 4k。这种降维技术可防止特征图的数量迅速增加。

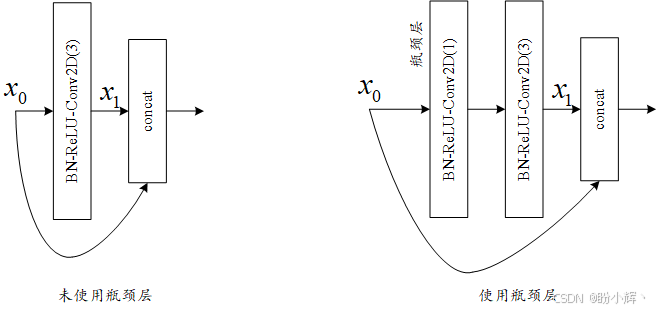
然后，瓶颈层将 DenseNet 层修改为 BN-ReLU-Conv2D(1)-BN-ReLU-Conv2D(3)，而不仅仅是 BN-ReLU-Conv2D(3)。将卷积核大小作为 Conv2D 的参数。对于瓶颈层，每个 Conv2D(3) 仅处理 4 k 4k 4k 特征图，而不是处理 l l l 层的 ( l -- 1 ) k + k 0 (l -- 1)k + k_0 (l--1)k+k0。例如，对于 101 层网络，最后一个 Conv2D(3) 的输入仍然是 48 个特征图，其中 k = 12。

为了解决特征图尺寸不匹配的问题，DenseNet 将深度网络划分为多个 Dense 块，这些块通过过渡层连接在一起。在每个密集块中，特征图的大小保持不变。

过渡层的作用是在两个 Dense 块之间从一个特征图大小过渡到较小的特征图大小。尺寸减小通常为一半。这是通过平均池化层完成的。过渡层的输入是前一个 Dense 块中最后一个串联层的输出。

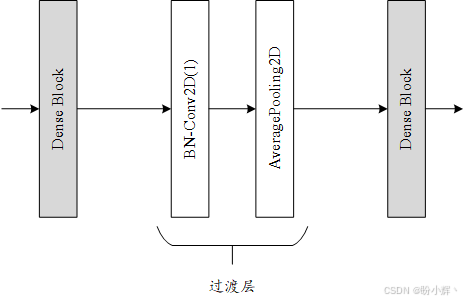
但是，在将特征图传递到平均池化之前，使用 Conv2D(1) 将其数量减少通过压缩因子 0 < θ < 1 0<θ<1 0<θ<1。 DenseNet 中使用 θ = 0.5 θ= 0.5 θ=0.5。例如，上一个 Dense 块的最后一个串联的输出为 (64,64,512)，则在 Conv2D(1) 之后，特征图的新尺寸为 (64,64,256)。压缩和降维在一起，过渡层由 BN-Conv2D(1)-AveragePooling2D 层组成。实际上，批归一化在卷积层之前。

2. 构建 DenseNet

我们已经介绍了 DenseNet 的重要概念。接下来，我们将使用 tf.keras 为 CIFAR10 数据集构建 DenseNet 模型。模型架构如下所示：

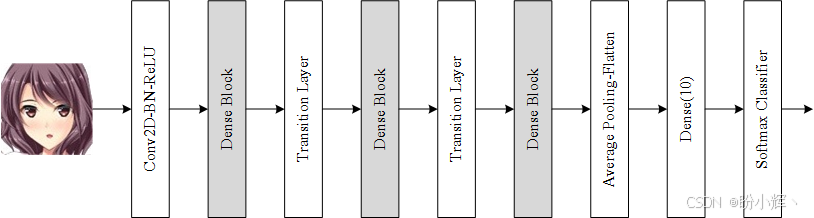
根据模型架构实现 DenseNet 模型：

python 复制代码

inputs = keras.layers.Input(shape=input_shape)
x = keras.layers.BatchNormalization()(inputs)
x = keras.layers.Activation('relu')(x)
x = keras.layers.Conv2D(num_filters_bef_dense_block,
        kernel_size=3,
        padding='same',
        kernel_initializer='he_normal')(x)
x = keras.layers.concatenate([inputs,x])

for i in range(num_dense_blocks):
    # 瓶颈层
    for j in range(num_bottleneck_layers):
        y = keras.layers.BatchNormalization()(x)
        y = keras.layers.Activation('relu')(y)
        y = keras.layers.Conv2D(4 * growth_rate,
                kernel_size=1,
                padding='same',
                kernel_initializer='he_normal')(y)
        if not data_augmentation:
            y = keras.layers.Dropout(0.2)(y)
        y = keras.layers.BatchNormalization()(y)
        y = keras.layers.Activation('relu')(y)
        y = keras.layers.Conv2D(growth_rate,
                kernel_size=3,
                padding='same',
                kernel_initializer='he_normal')(y)
        if not data_augmentation:
            y = keras.layers.Dropout(0.2)(y)
        x = keras.layers.concatenate([x,y])
    if i == num_dense_blocks - 1:
        continue

    #压缩特征图数量，并减小特征图尺寸
    num_filters_bef_dense_block += num_bottleneck_layers * growth_rate
    num_filters_bef_dense_block = int(num_filters_bef_dense_block * compression_factor)
    y = keras.layers.BatchNormalization()(x)
    y = keras.layers.Conv2D(num_filters_bef_dense_block,
        kernel_size=1,
        padding='same',
        kernel_initializer='he_normal')(y)
    if not data_augmentation:
        y = keras.layers.Dropout(0.2)(y)
    x = keras.layers.AveragePooling2D()(y)

x = keras.layers.AveragePooling2D(pool_size=8)(x)
x = keras.layers.Flatten()(x)
outputs = keras.layers.Dense(num_classes,
        kernel_initializer='he_normal',
        activation='softmax')(x)

model = keras.Model(inputs=inputs,outputs=outputs)
model.compile(loss='categorical_crossentropy',
        optimizer=keras.optimizers.RMSprop(1e-3),
        metrics=['acc'])
model.summary()

使用 tf.keras 实现的 DenseNet 模型训练 200 个 epoch 后，准确率达到 93.74%，训练过程中采用了数据增强技术，如果需构建更深层的 DenseNet 模型，需调整 growth_rate 和 depth 参数。