文章目录
图形学的依赖知识

本节课任务


向量
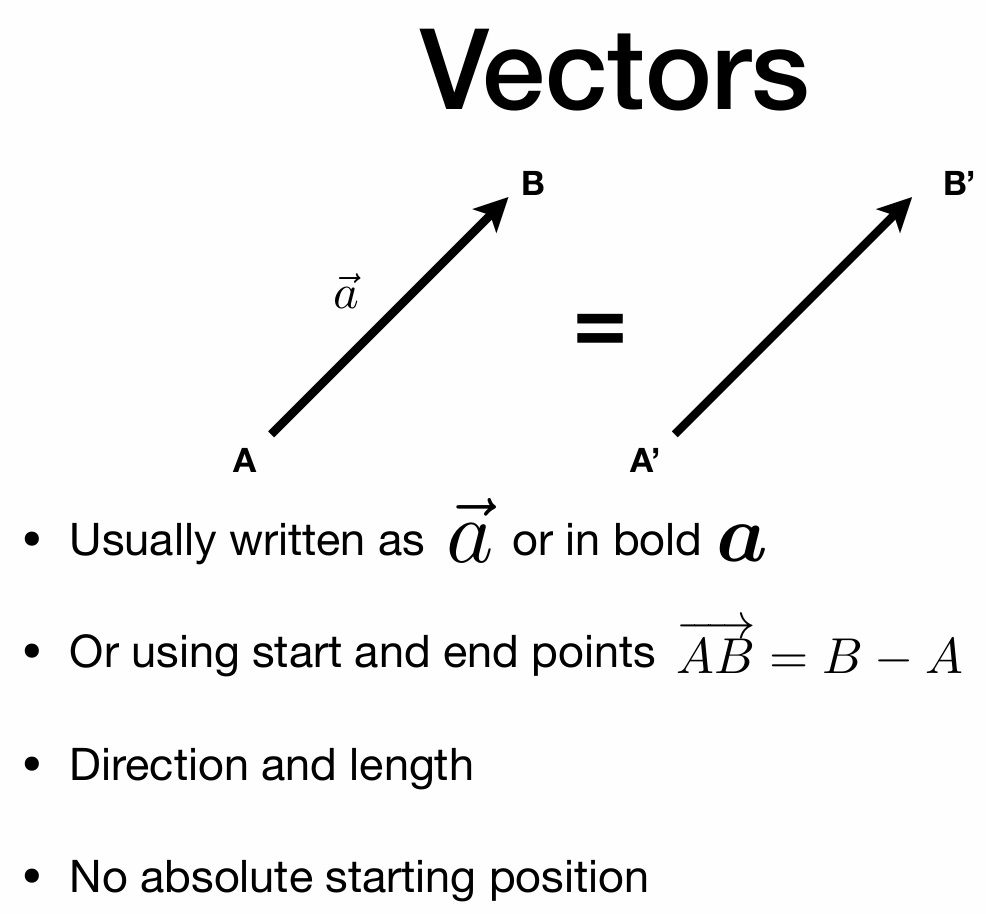
向量标准化

向量加法
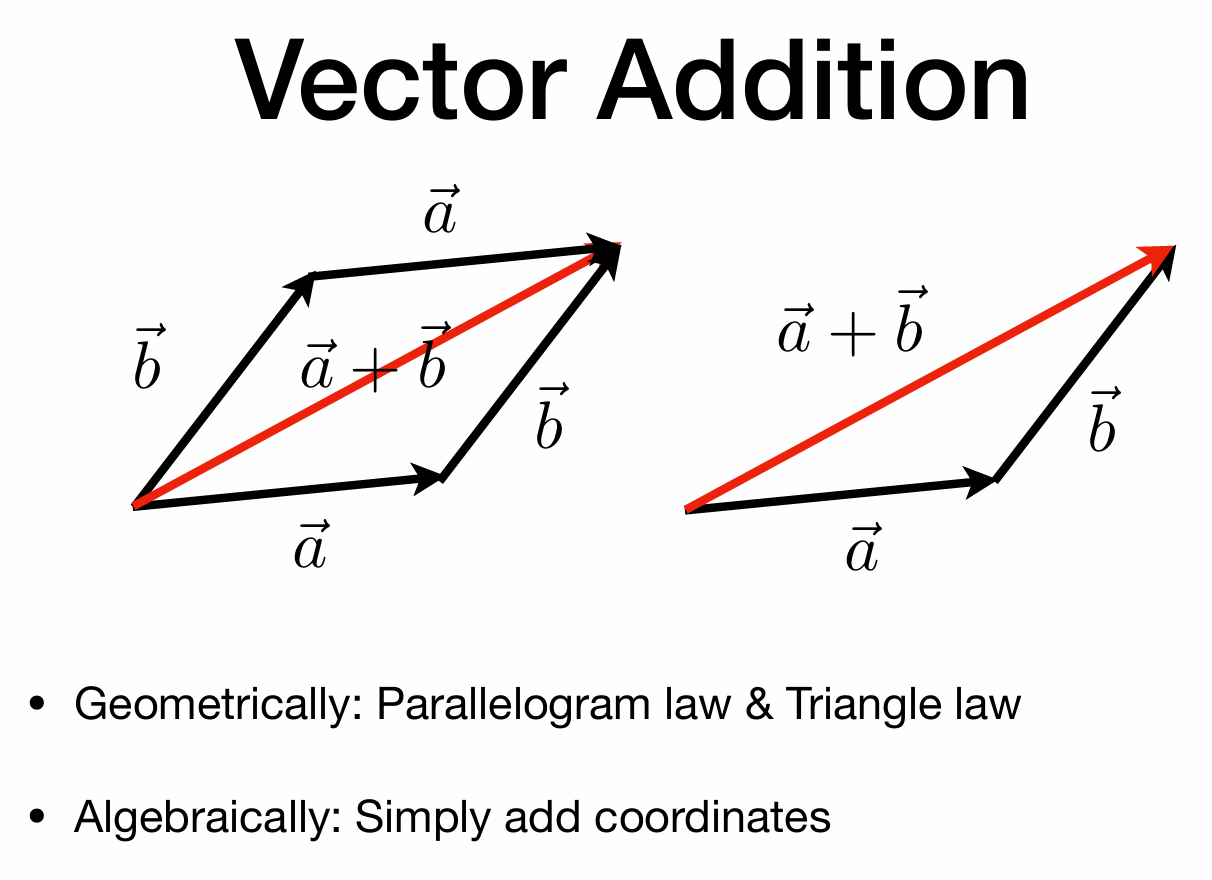
笛卡尔坐标系

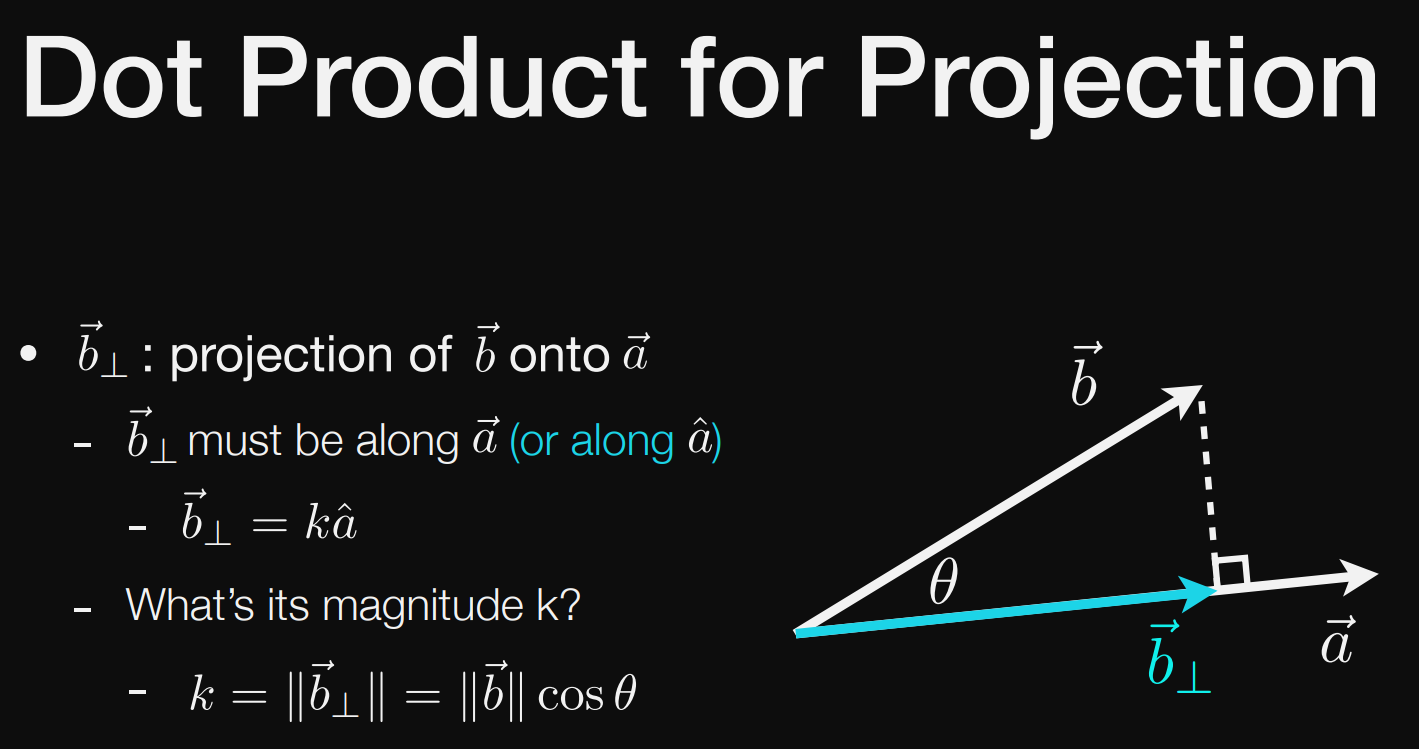
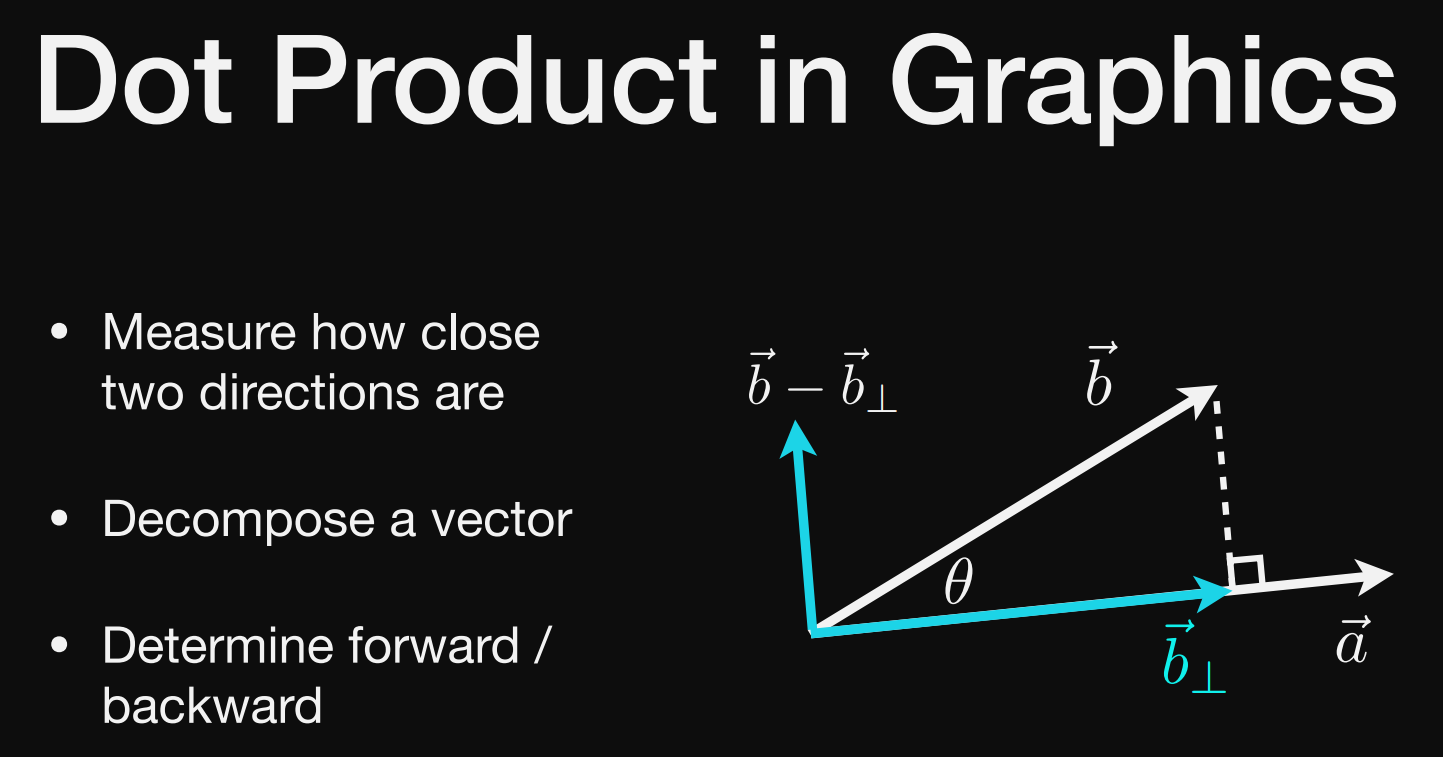
向量的点乘
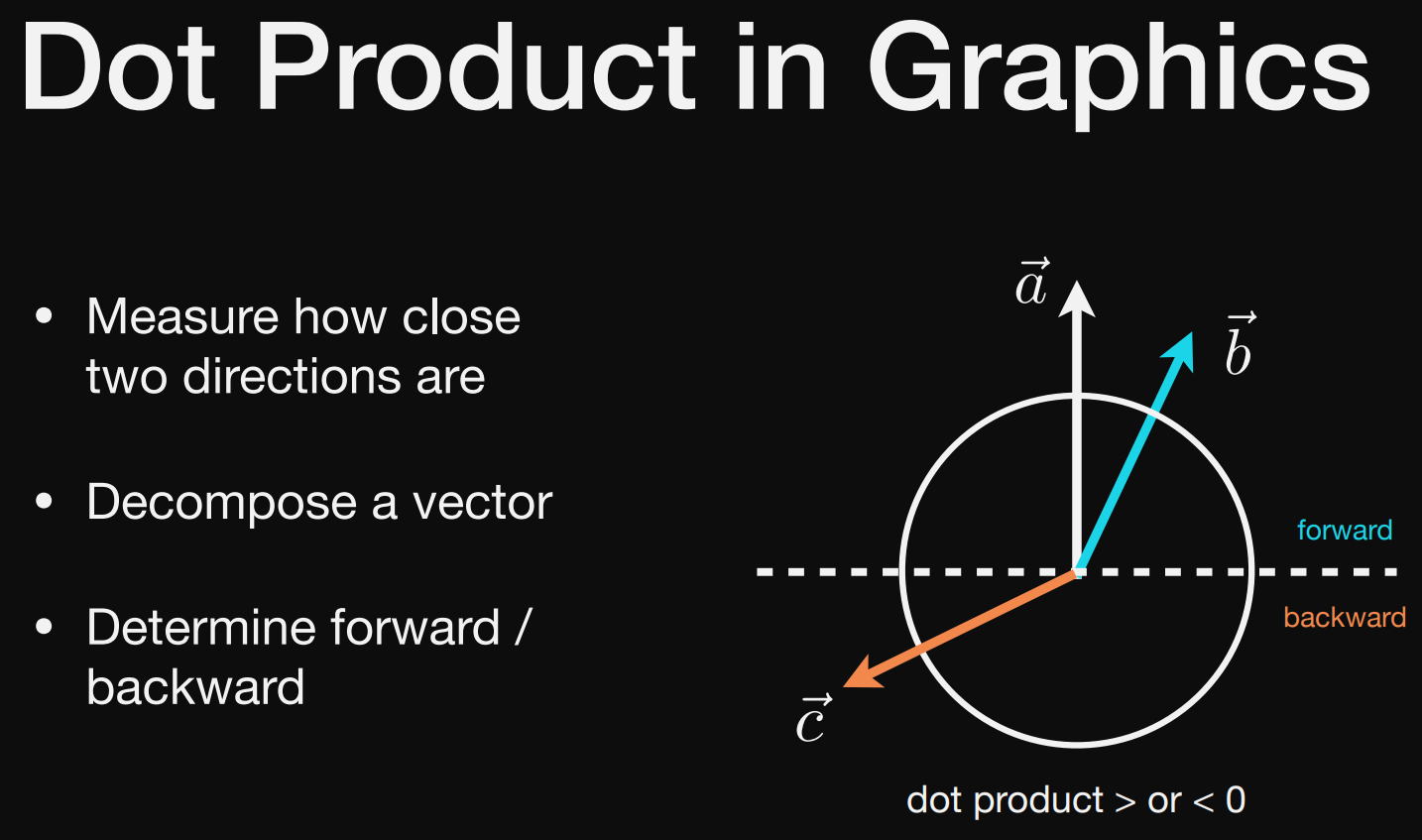
可以判断向量前与后的信息
点乘>0 同方向
点乘<0 反方向
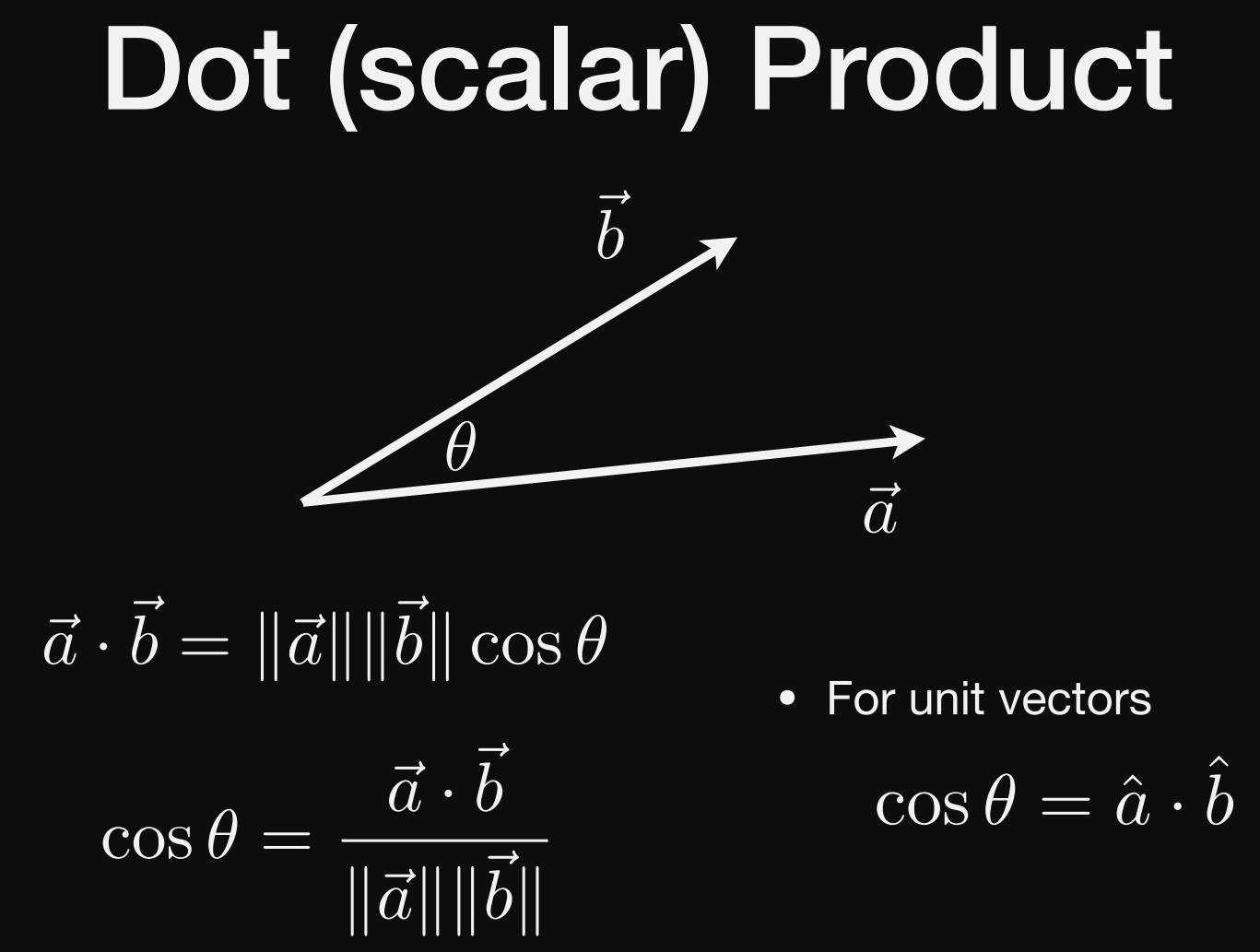
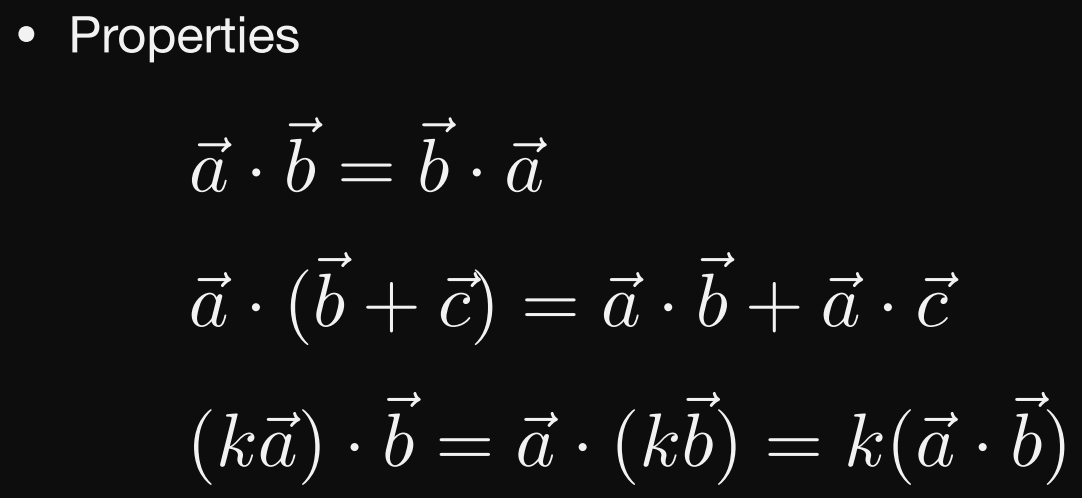

perpendicular 垂直

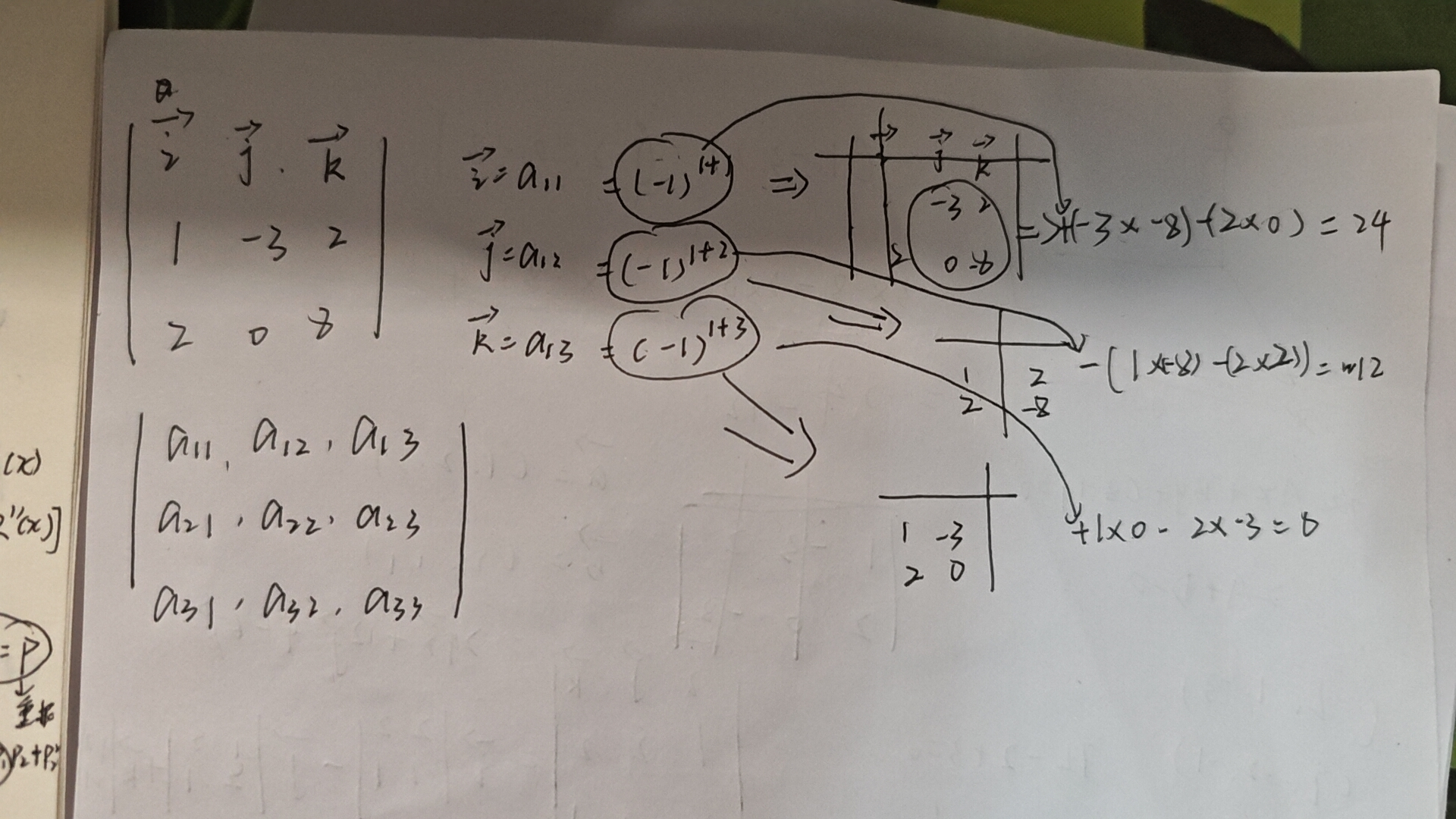
向量的叉乘
输入两个向量,输出一个同时垂直与这两个向量的新向量
如何判断新向量的方向?
右手螺旋定则
如a×b=c
四指从a的方向向b的方向握紧,大拇指指向的就是c的方向



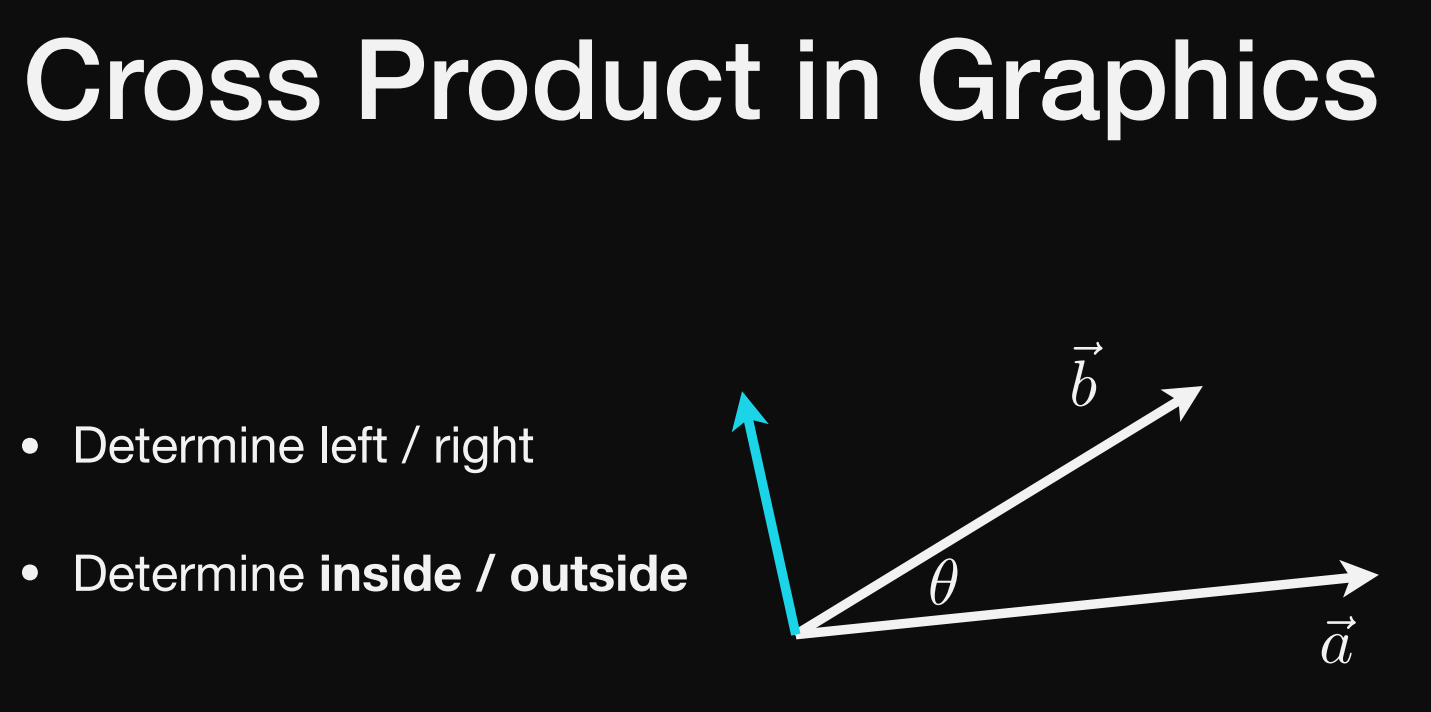
如何判断两个向量的左右关系?
a×b得到结果是和z轴同向,是正的,说明b在a的左侧
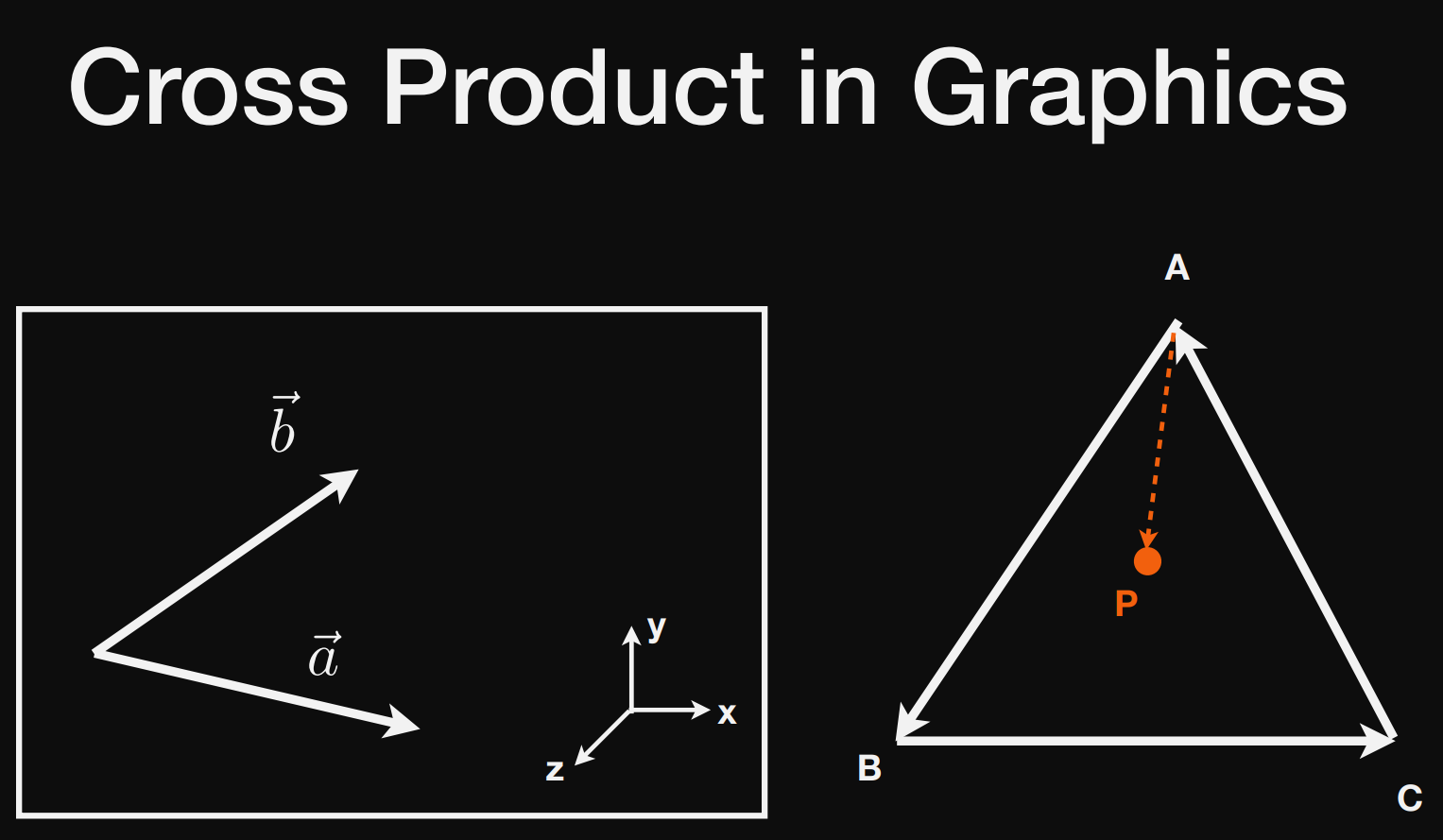
如何判断一个点是否落在三角形内部?(做光栅化,给三角形内部的像素着色需要用到)
AB×AP > 0 说明P在AB左侧
BC×BP > 0 说明P在BC左侧
CA×CP > 0 说明P在CA左侧
说明点P落在三角形ABC内部
正交坐标系


矩阵


矩阵乘法





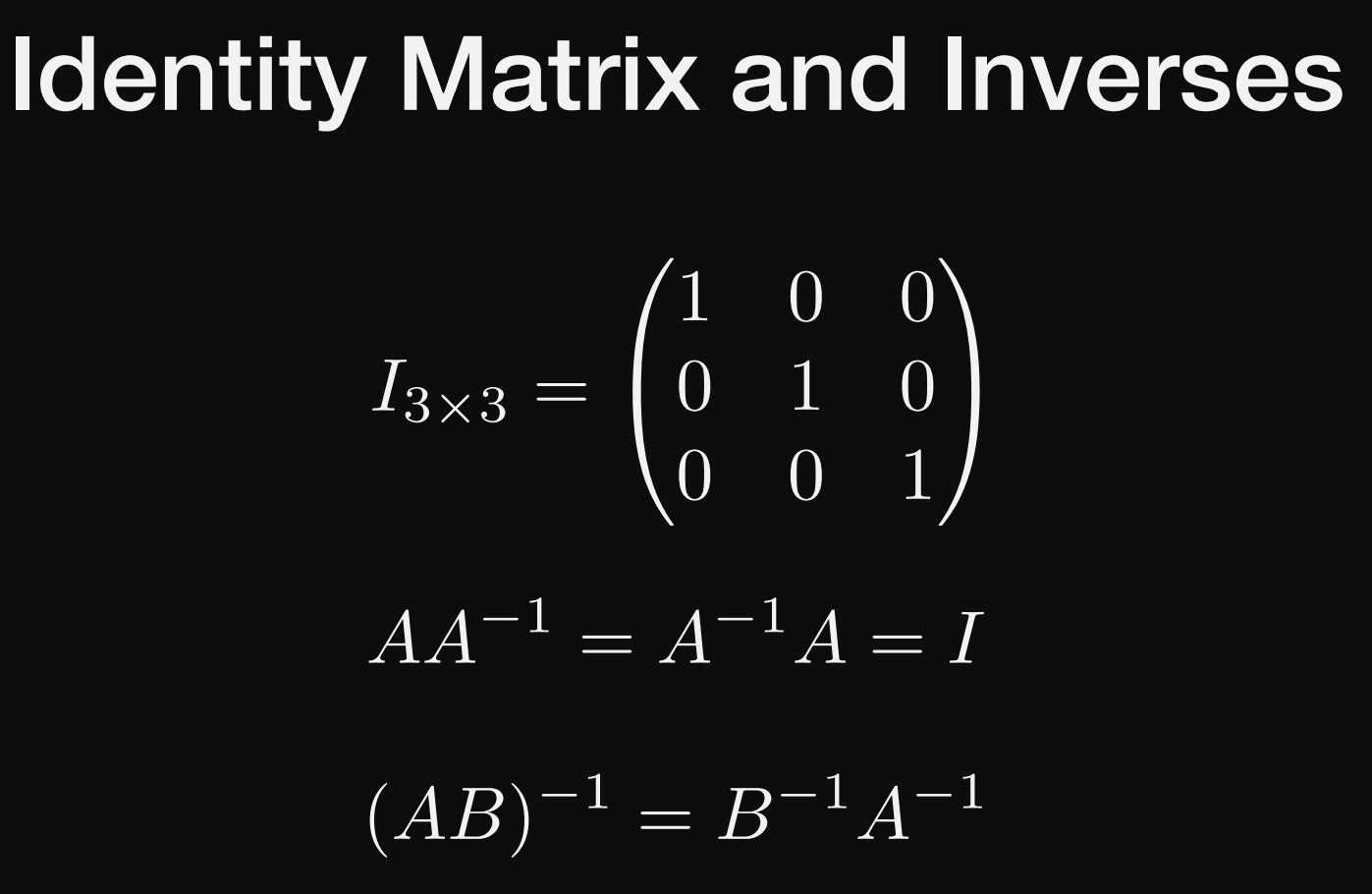
向量的叉乘(矩阵形式)
将a向量重新组织,变为A*这个矩阵,A*这个矩阵叫a向量的反对称矩阵(Skew-Symmetric Matrix)

(为什么PPT中写的是DualMatrix(对偶矩阵?)呢?此处的"对偶"并非线性代数中"对偶空间"的标准定义,而是强调向量与叉乘矩阵的等价性。叉乘矩阵可视为向量的一种"对偶表示",使得几何操作(如旋转)可通过矩阵运算实现。计算机图形学中,这种术语是约定俗成的,目的是直观表达向量与矩阵形式的对应关系)
A*乘以b就是axb的结果

之后我会持续更新,如果喜欢我的文章,请记得一键三连哦,点赞关注收藏,你的每一个赞每一份关注每一次收藏都将是我前进路上的无限动力 !!!↖(▔▽▔)↗感谢支持!