代码随想录算法训练营第21天 -- 回溯4 || 491.非递减子序列 / 46.全排列 /47.全排列 II
491.非递减子序列
解题思路
首先这道题默认不能对数组进行排序,先自己画一下树状图:
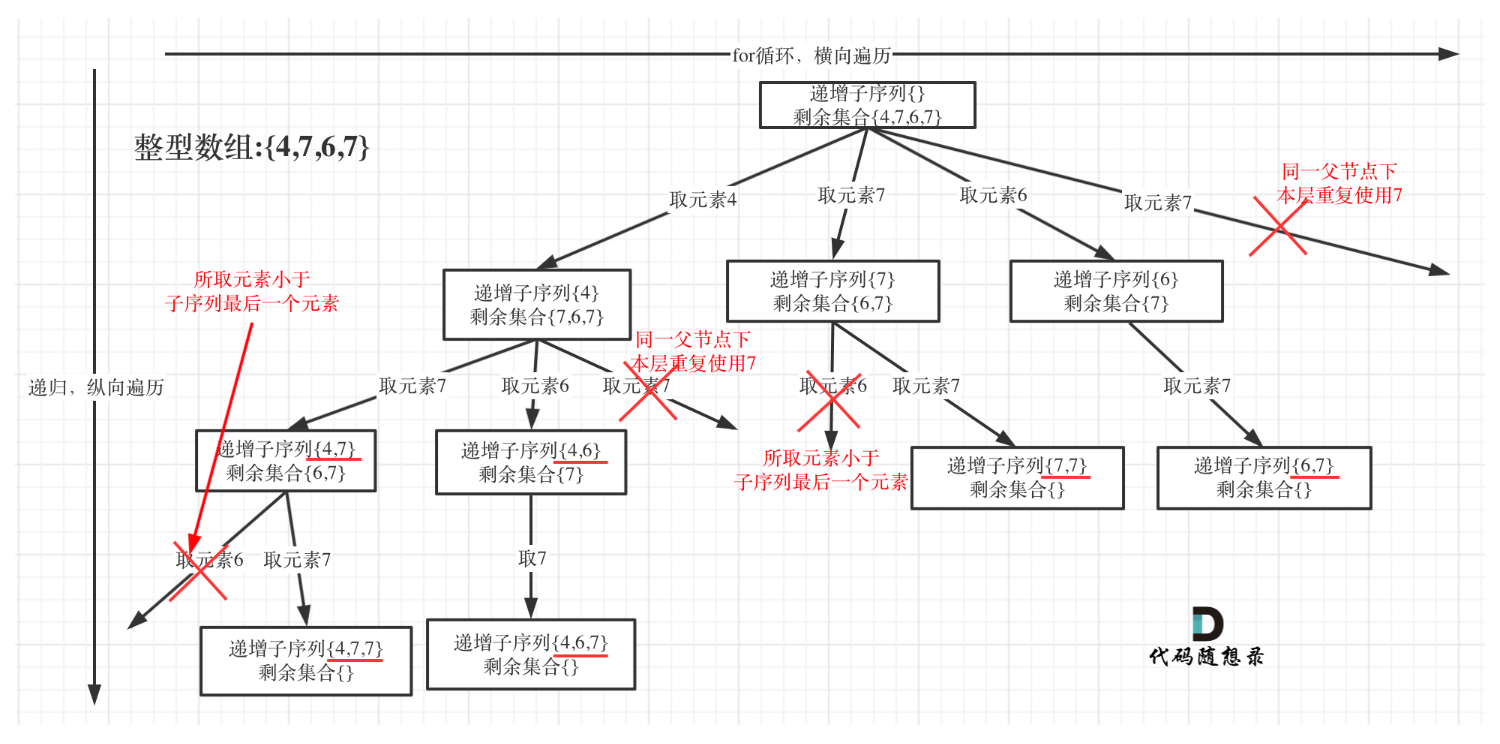
本题设计到树层去重。
对于子集问题,无递归终止条件。
对于本题,当数组元素个数大于等于2时,才可以,这是其中一个条件;
其次,集合第一个元素要大于等于子序列的最后一个元素;
对于树层去重,对于本题不能使用used数组,因为本题的序列不是单调的,相同的数可能不挨在一起,但我们依然要做树层去重,这里我们使用哈希 unordered_set 进行去重,并且我们让其在 for 循环外面,保证每次递归都重新定义一个哈希 set,这样回溯我们就不用对 set 进行 pop 操作了。
完整代码如下:
cpp
class Solution {
public:
vector<int> path;
vector<vector<int>> res;
void backtracking(vector<int>& nums, int startindex) {
if (path.size() > 1) res.push_back(path);
unordered_set<int> uset;
for (int i = startindex; i < nums.size(); i ++) {
if (!path.empty() && nums[i] < path.back() || uset.find(nums[i]) != uset.end())
continue;
uset.insert(nums[i]);
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
backtracking(nums, 0);
return res;
}
};我解释一下 if 里的条件:
首先我们得两个条件:nums[i] < path.back() 和 uset已经有这个元素,这两个元素成立一个就 continue 操作;但对于第一个条件,我们需要保证 path 数组非空,所以加了一个非空判断。
46.全排列
解题思路
本题进入排列专题。
排列问题不需要startindex参数,因为当取第二个数的时候,树枝还可以再取第一个数,只是顺序不同而已。
排列问题需要利用used数组,用来记录哪个位置的数取过,哪个位置的数没取过。
排列问题纵向遍历的深度由数组大小决定。
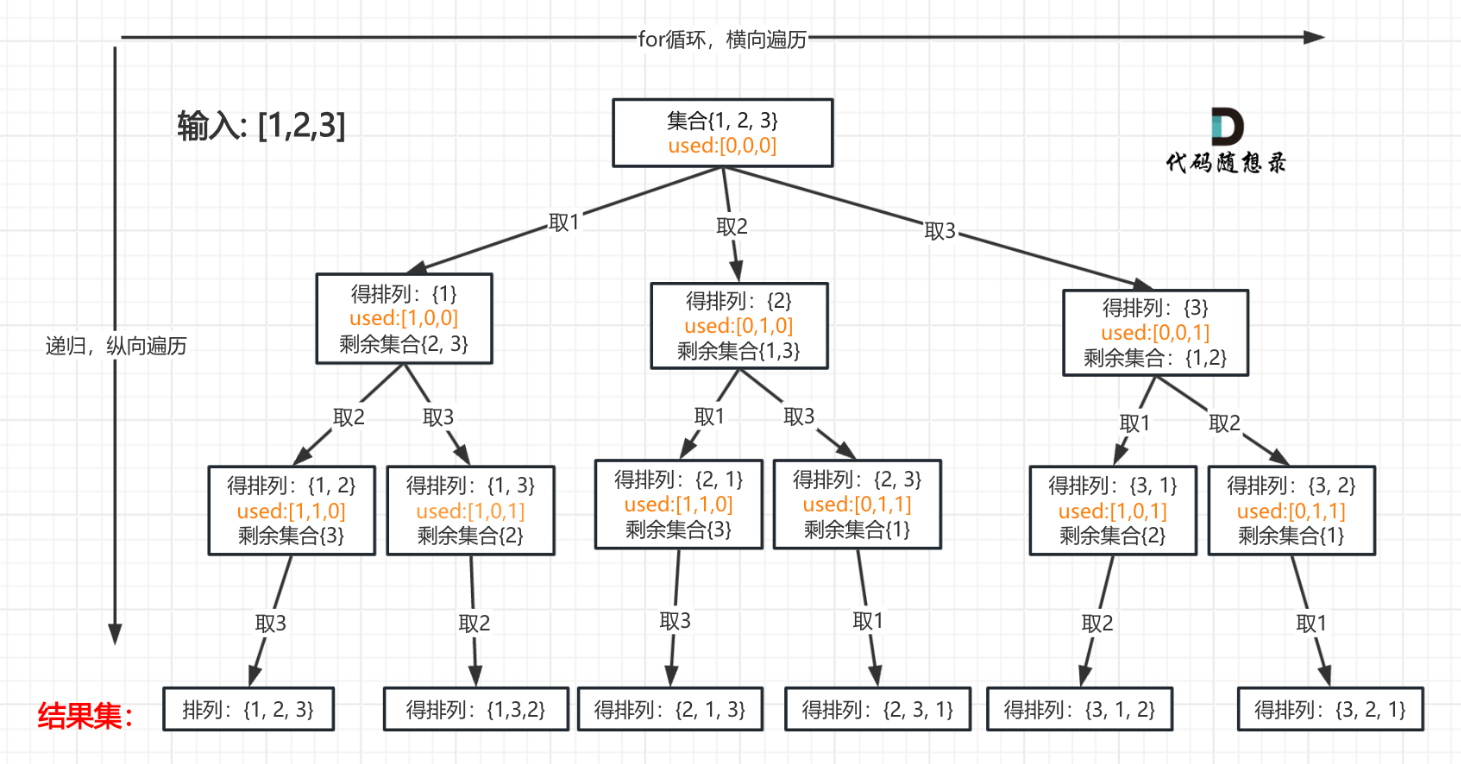
完整代码:
cpp
class Solution {
public:
vector<int> path;
vector<vector<int>> res;
void backtracking(vector<int>& nums, vector<bool>& used) {
if (path.size() == nums.size()) {
res.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i ++) {
if (used[i] == true) continue;
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, used);
used[i] = false;
path.pop_back();
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return res;
}
};47.全排列II
解题思路
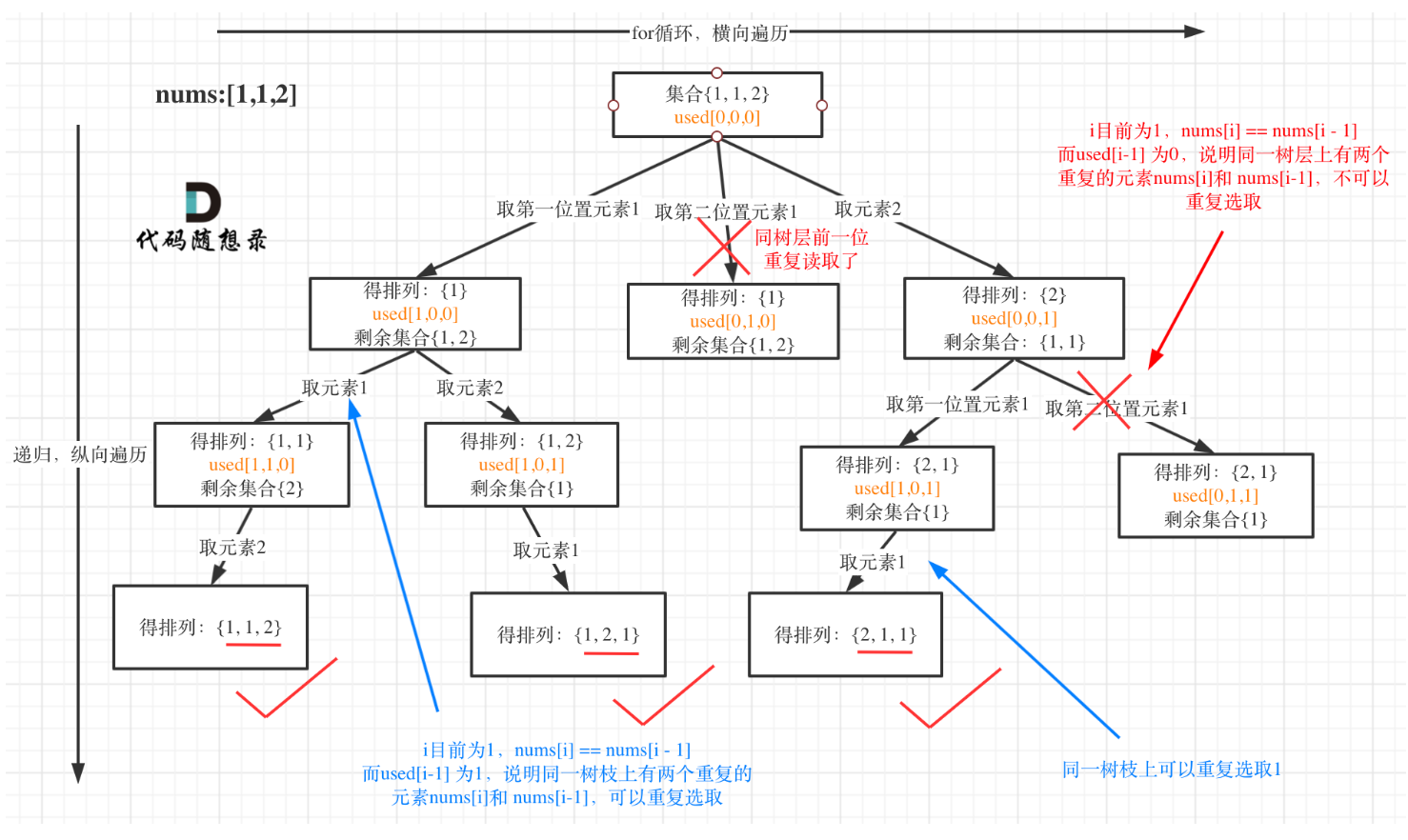
本题和上一题的区别就在于本题需要去重,对于去重操作,无非就是多了两行代码操作,对树层进行去重:
cpp
if (i && nums[i] == nums[i - 1] && used[i - 1] == false)
continue;除此之外,本题还需要先对数组进行排序,然后再进行上一题和去重的操作
完整代码如下:
cpp
class Solution {
public:
vector<int> path;
vector<vector<int>> res;
void backtracking(vector<int>& nums, vector<bool>& used) {
if (path.size() == nums.size()) {
res.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i ++) {
if (i && nums[i] == nums[i - 1] && used[i - 1] == false)
continue;
if (used[i] == true) continue;
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(), nums.end());
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return res;
}
};去重细节
本题其实,树枝去重和树层去重都可以,下面以 [1, 1, 1] 为例,画出树层去重和树枝去重的两个树状图。
树层去重:
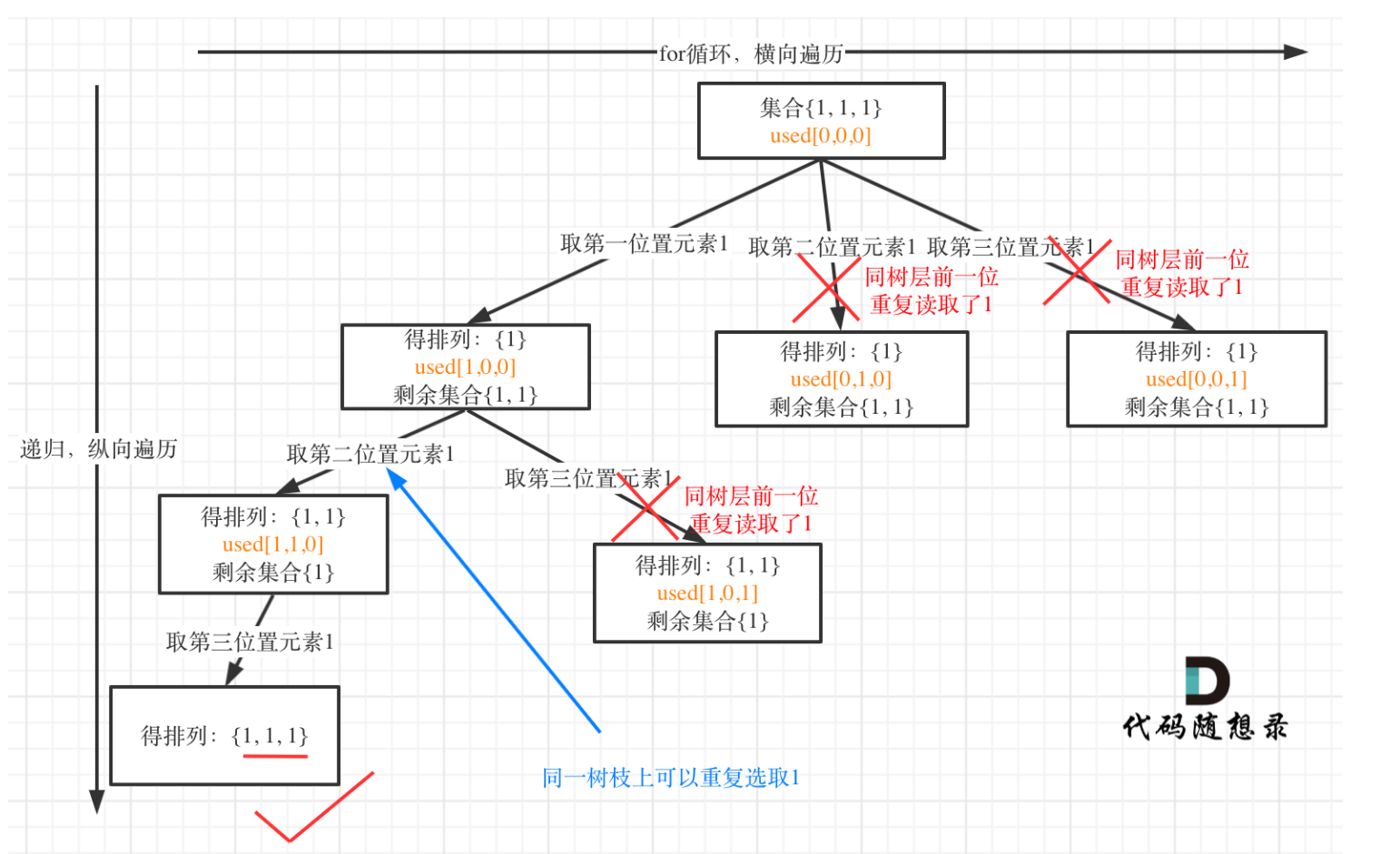
树枝去重:
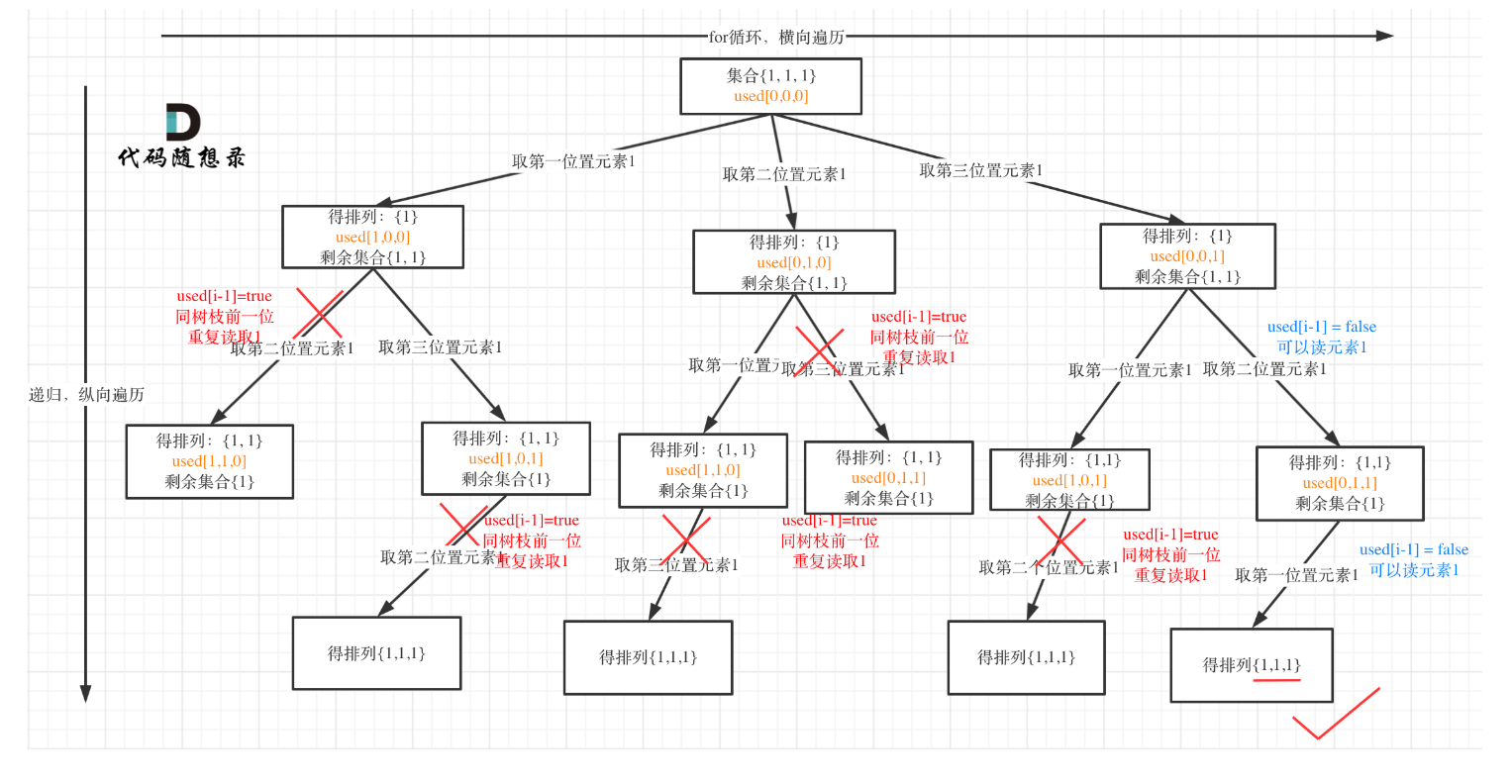
所以,在去重操作的代码中,false 也可以写成 true
cpp
if (i && nums[i] == nums[i - 1] && used[i - 1] == true)
continue;上述代码也是正确的。
但是,一般树枝去重的效率不如树层去重,我们会优先选择树层去重。