这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!
**一、**合适的聚类粒度
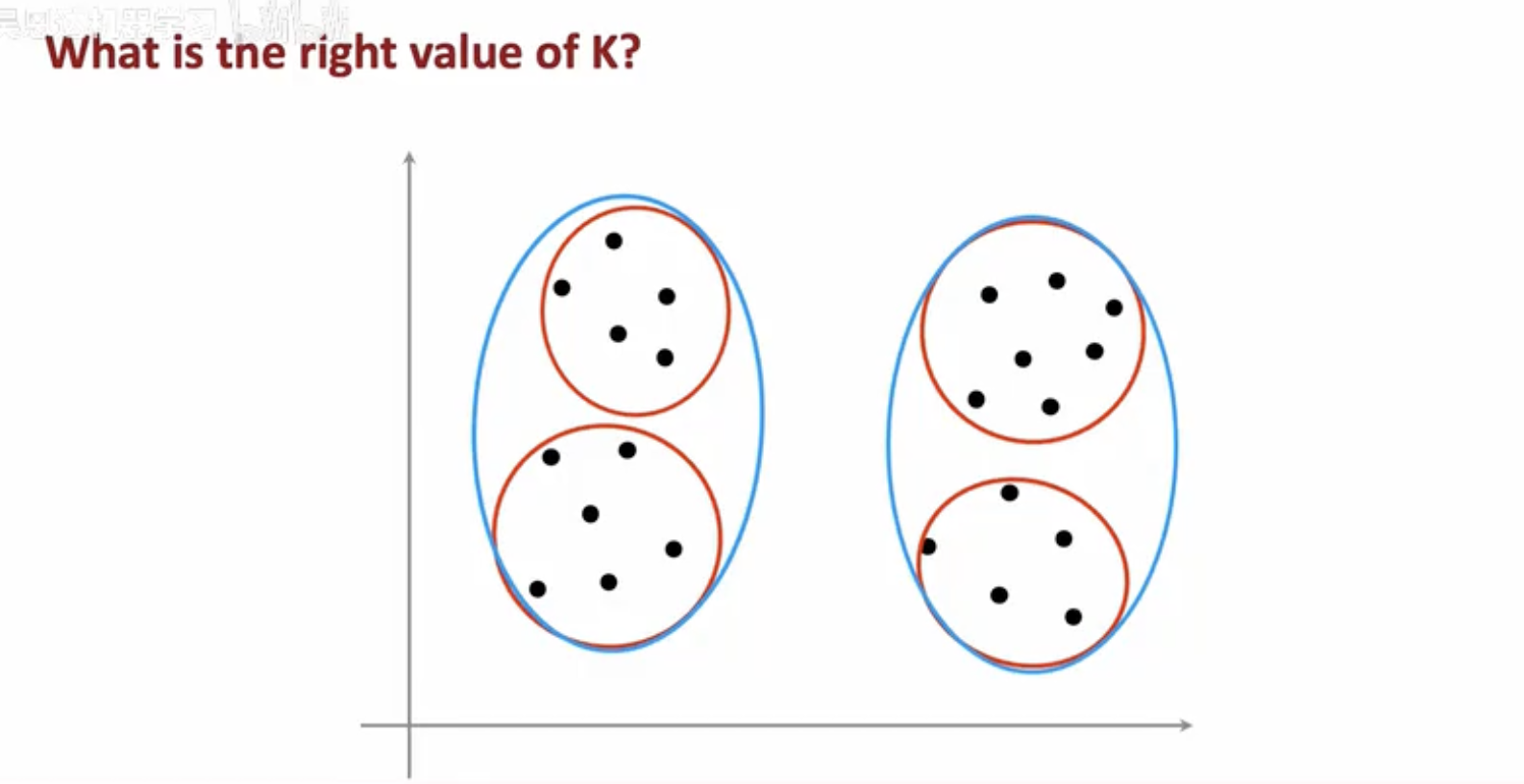
图中黑点为数据样本。每一侧的蓝色大椭圆把样本划成两类(K=2,按"左右/宏观簇"分组);而蓝色椭圆内部又各有两个红色小圆,把样本进一步细分为四类(K=4,按"子簇/细粒度"分组)。同一数据既可视作两个大的聚类,也可视作四个更紧密的子聚类,直观展示了"正确的 K 取决于你想识别的粒度"。
**二、**肘部法确定 K
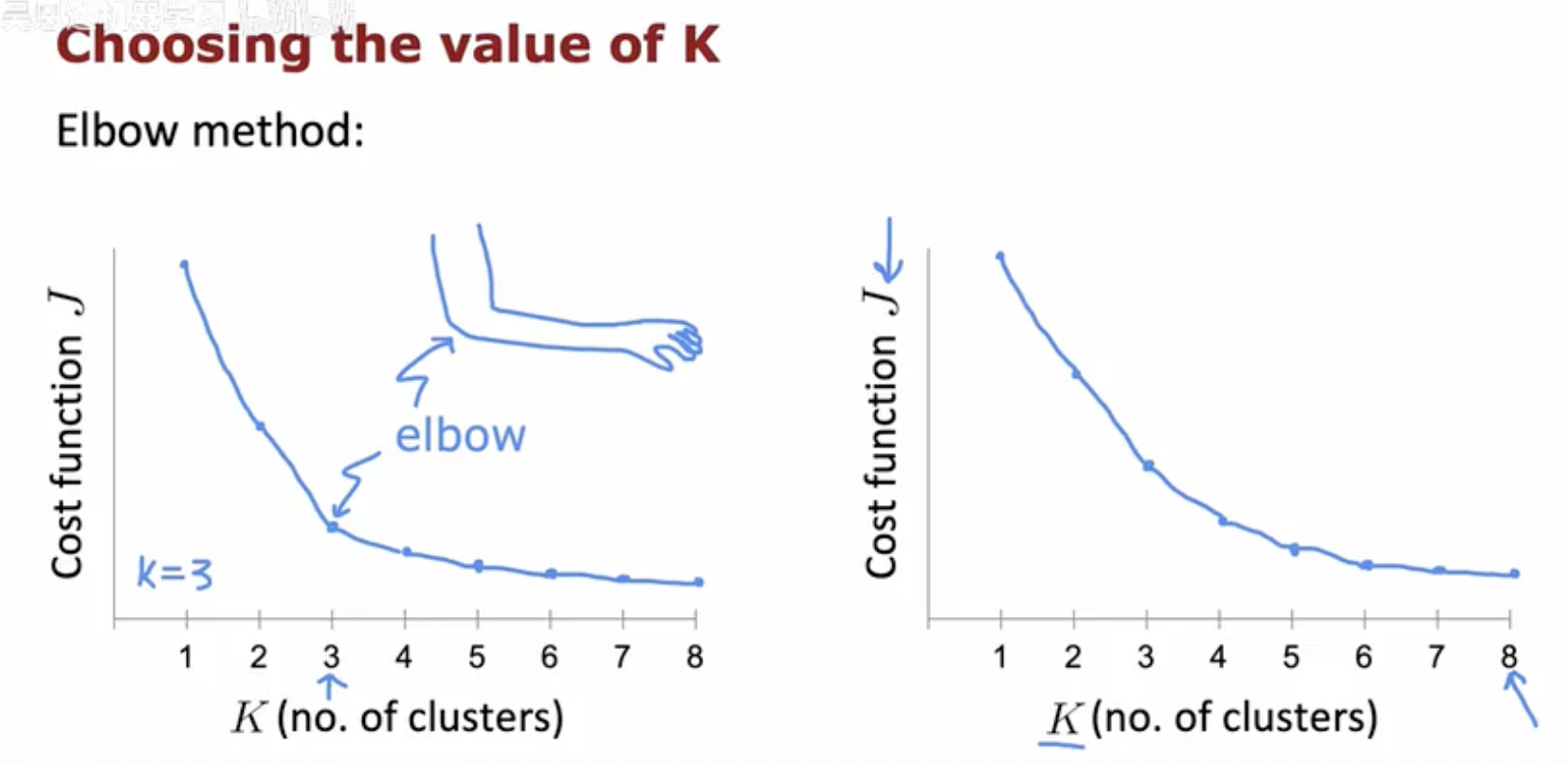
图示主题是"Choosing the value of K(选择 K 的取值)--- Elbow method(肘部法)"。
左图:纵轴为代价函数 J,横轴为簇数 K。曲线在 K=1→3 之间快速下降,到了 K≈3 处出现明显"拐点"(图中用手臂与"elbow"标注),之后增加簇数收益变小、曲线趋缓,因此图上给出结论 k=3。
右图:同样坐标设置,但曲线从 K=1 到更大的 K 基本平滑下降,没有明显"拐点",表示用肘部法难以从这条曲线中确定一个清晰的 K 值。
**三、**按需求选择 K
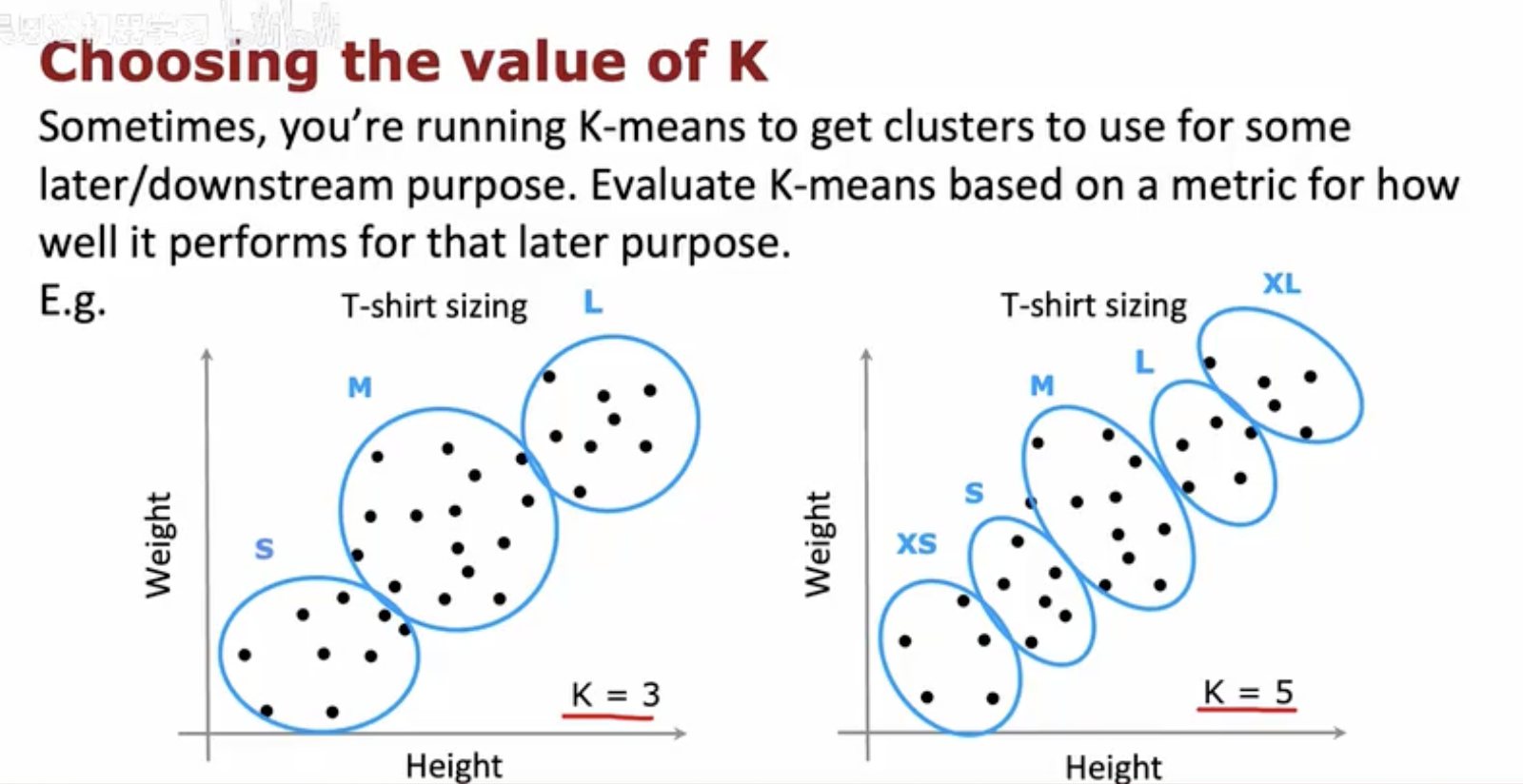
图示主题是"Choosing the value of K",强调按下游用途选择簇数。
上方文字:有时运行 K-means 是为后续任务提供分组,应根据该后续任务的指标评估 K 值。
两幅示例(横轴 Height,纵轴 Weight,黑点为样本,蓝色椭圆为簇):
-
左图"T-shirt sizing":将人群按身高与体重聚为 3 类并对应 S、M、L,标注 K=3。
-
右图"T-shirt sizing":同一数据更细分为 5 类并对应 XS、S、M、L、XL,标注 K=5。
含义:同一数据可因目标不同采用不同的 K,从而得到粗或细的尺码分组。
四、总结
在 K-means 聚类中,选择合适的聚类个数 KK 是一个核心问题。不同的 K 值往往对应不同层次的划分,没有唯一的"正确答案"。常见的思路包括:
-
聚类粒度:根据需要,可以把数据分为较少的大簇,也可以细分为更多的小簇,这取决于研究者希望看到的粒度。
-
评估方法:利用如肘部法等技术手段,寻找代价函数下降明显放缓的位置,以此作为较合理的聚类数。
-
任务导向:有时聚类的最终目的是为下游应用服务,此时 K 的选择应围绕实际需求来决定,例如分组标准是粗略还是精细。
综上,聚类个数的选择不是一个纯粹的数学问题,而是 方法评估与应用需求结合的结果。既要考虑统计意义上的合理性,也要兼顾任务目标的适配性,最终找到最有价值的 K。
这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!