文章目录
寻找数组的中心下标
题目链接
题目描述

解法
本题需要预处理两个前缀和数组,分别计算数组前部分的和与后部分的和,然后比较两者是否相等,即可求出目标下标。
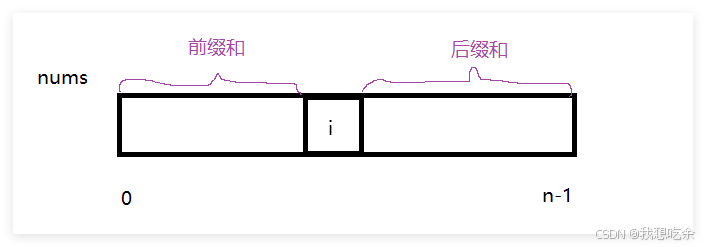
具体逻辑如下:
【注意】
因为nums下标是以0开始计算的,所以递推公式不能按部就班,需要特殊处理。这里也启示我们:不要死记硬背,理解原理乃上上策!!!
- 预处理一个前缀和数组f,下标从1开始计算
f[i]表示区间[0,i-1]所有元素的和
如何递推?
看图:
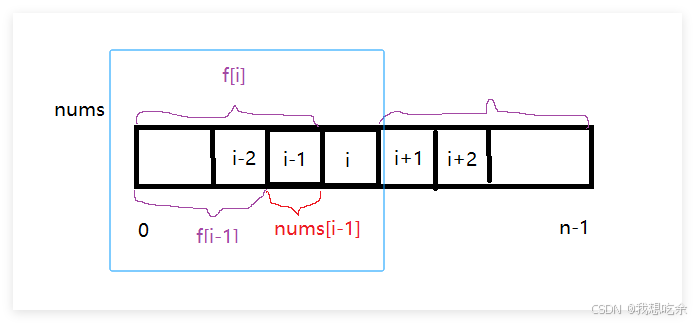
不难看出:
f [ i ] = f [ i − 1 ] + n u m s [ i − 1 ] f[i]=f[i-1]+nums[i-1] f[i]=f[i−1]+nums[i−1]
注意:从左向右递推
- 预处理一个前缀和数组g,下标从1开始计算
g[i]表示区间[i+1,n-1]所有元素的和
看图:
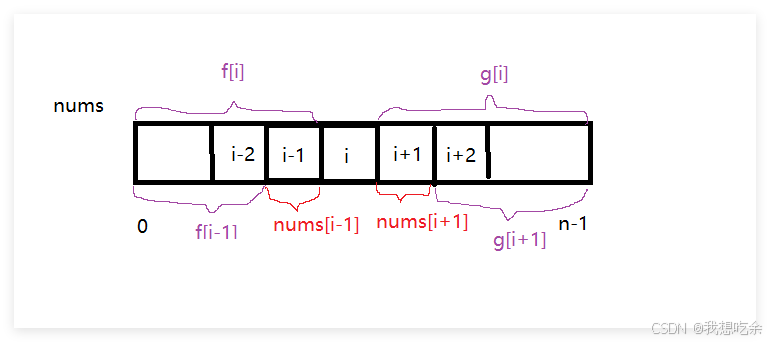
g [ i ] = g [ i + 1 ] + n u m s [ i + 1 ] g[i]=g[i+1]+nums[i+1] g[i]=g[i+1]+nums[i+1]
注意:从右向左递推
-
使用前缀和数组找出目标下标
遍历数组,判断
f[i] == g[i]即可,是则直接返回下标 -
细节问题
- 注意边界情况
- 当
i=0时,f会越界,设置f(0) = 0即可 - 当
i=n-1时,g会越界,设置g(n-1) = 0即可
当然,如果我们使用的是vector的话,就不用担心这个问题了,因为vector的对象创建时,所有元素会初始化为0。
- 当
- 代码
cpp
class Solution {
public:
int pivotIndex(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n);
vector<int> g(n);
//预处理前缀和数组
for(int i = 1; i < n; ++i)
f[i] = f[i-1] + nums[i-1];
//预处理后缀和数组
for(int i = n - 2; i >= 0; --i)
g[i] = g[i+1] + nums[i+1];
//寻找结果
for(int i = 0; i < n; ++i)
if(f[i] == g[i]) return i;
//无结果返回-1
return -1;
}
};除自身以外数组的乘积
题目链接
题目描述

解法
前缀积
前缀积与前缀和的思想一摸一样,将加换成乘即可,但还需处理一些细节问题。
具体逻辑如下:
该题逻辑与上一题类似,需要处理两个前缀积:
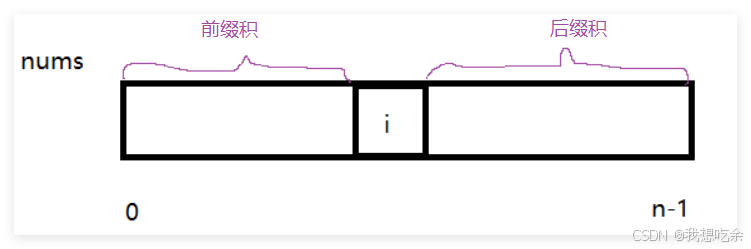
- 预处理前缀积f以及后缀积g
f[i]表示区间[0,i-1]所有元素的积g[i]表示区间[i+1,n-1]所有元素的积
递推公式推导也和上一题类似,看图:
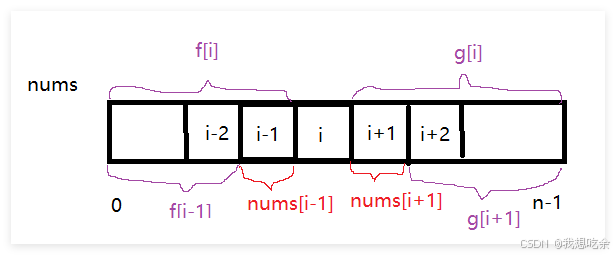
不难看出:
f [ i ] = f [ i − 1 ] ∗ n u m s [ i − 1 ] f[i]=f[i-1]*nums[i-1] f[i]=f[i−1]∗nums[i−1]从左向右递推
g [ i ] = g [ i + 1 ] ∗ n u m s [ i + 1 ] g[i]=g[i+1]*nums[i+1] g[i]=g[i+1]∗nums[i+1]从右向左递推
-
使用前后缀积解决问题
定义目标数组ret
r e t [ i ] = f [ i ] ∗ g [ i ] ret[i]=f[i]*g[i] ret[i]=f[i]∗g[i]用该公式遍历填充ret即可
-
细节问题
处理边界问题:
- 当
i=0时,f会越界,设置f(0) = 1即可 - 当
i=n-1时,g会越界,设置g(n-1) = 1即可
注意:千万不要设置成0了,否则所有元素都会递推为0.
- 当
-
代码:
cpp
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums)
{
int n = nums.size();
vector<int> f(n);
vector<int> g(n);
//预处理前缀积数组
f[0] = 1;//处理边界情况
for(int i = 1; i < n; ++i)
f[i] = f[i-1] * nums[i-1];
//预处理后缀积数组
g[n-1] = 1;
for(int i = n-2; i >= 0; --i)
g[i] = g[i+1] * nums[i+1];
//使用
vector<int> ret(n);
for(int i = 0; i < n; ++i)
ret[i] = f[i] * g[i];
return ret;
}
};