目录
[（一） 空域图像增强](#（一） 空域图像增强)
[1. 空域低通滤波](#1. 空域低通滤波)
[（1） 中值滤波器](#（1） 中值滤波器)
[（2） 高斯滤波器](#（2） 高斯滤波器)
[2. 空域高通滤波器](#2. 空域高通滤波器)
[（1） 拉普拉斯算子](#（1） 拉普拉斯算子)
[（2） 非锐化掩蔽](#（2） 非锐化掩蔽)
[（3） 梯度](#（3） 梯度)
[（4） Canny 边缘检测](#（4） Canny 边缘检测)
[（二） 时域图像增强](#（二） 时域图像增强)
[（1） 一维傅里叶变换](#（1） 一维傅里叶变换)
[（2） 二维傅里叶变换](#（2） 二维傅里叶变换)
[（3） 快速傅里叶变换](#（3） 快速傅里叶变换)
[（三） 色阶调整去雾技术](#（三） 色阶调整去雾技术)
[（1） 概述](#（1） 概述)
[（2） 暗通道去雾原理](#（2） 暗通道去雾原理)
[（3） 暗通道去雾实例](#（3） 暗通道去雾实例)
[（四） 直方图均衡化去雾技术](#（四） 直方图均衡化去雾技术)
[（1） 色阶调整原理](#（1） 色阶调整原理)
[（2） 自动色阶图像处理算法](#（2） 自动色阶图像处理算法)
一、引言
雾霾天气往往会给人们的生产和生活带来极大不便，也大大增加了交通事故的发生率。一般而言，在恶劣天气（如雾天、雨天等）条件下，户外景物图像的对比度和颜色会改变或退化，图像中蕴含的许多特征也会被覆盖或模糊。这会导致某些视觉系统（如电子卡口、门禁监控等）无法正常工作。因此，从在雾霾天气下采集的退化图像中复原和增强景物的细节信息具有重要的现实意义。数字图像处理技术已被广泛应用于科学和工程领域，如地形分类系统、户外监控系统、自动导航系统等。为了保证视觉系统全天候正常工作，就必须使视觉系统适应各种天气状况。
二、图像去雾的各类技术
（一） 空域图像增强
图像增强技术的主要目标是，通过对图像的处理，使图像比处理前更适合一个特定的应用，比如去除噪声等，来改善一幅图像的视觉效果。
图像增强的方法分为两大类：空间域图像增强和频域图像增强，这里所要介绍的均值滤波、中值滤波、拉普拉斯变换等就是空间域图像增强的重要内容。
1. 空域低通滤波
使用空域模板进行的图像处理，被称为空域滤波。空域滤波的机理就是在待处理的图像中逐点地移动模板，滤波器在该点的响应通过事先定义的滤波器系数与滤波模板扫过区域的相应像素值的关系来计算。中值滤波是空域低通滤波的典型代表。
（1） 中值滤波器
中值滤波器属于非线性滤波器，中值滤波是对整幅图像求解中位数的过程。具体实现时用一个模板扫描图像中的每一个像素，然后用模板范围内所有像素的中位数像素代替原来模板中心的像素。例如，图 1 中图像中 150 灰度的像素在中值滤波后灰度将会取值为 124。
|-----|-----|-----|-----|-----|
| 123 | 125 | 126 | 130 | 140 |
| 122 | 124 | 126 | 127 | 135 |
| 118 | 120 | 150 | 125 | 134 |
| 119 | 115 | 119 | 123 | 133 |
| 111 | 116 | 110 | 120 | 130 |
[图1 中值滤波模板]
邻近值：115, 119, 120, 123, 124,125, 126, 127, 150
中值滤波值：124
中值滤波器实例演示：
python
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文显示问题
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# ---------------------- 1. 中值滤波函数 ----------------------
def get_median(data):
"""计算列表的中位数"""
data_sorted = sorted(data)
half = len(data_sorted) // 2
return data_sorted[half]
def my_median_blur_gray(image, size):
"""灰度图像中值滤波"""
image_copy = image.copy() # 复制图像，防止原图像被篡改
data = []
sizepart = int(size / 2) # 滤波核半大小（用于边界判断）
for i in range(image_copy.shape[0]): # 遍历行（高度）
for j in range(image_copy.shape[1]): # 遍历列（宽度）
# 收集滤波核内的像素值（边界外像素忽略）
for ii in range(size):
for jj in range(size):
# 计算当前滤波核像素在原图的坐标
x = i + ii - sizepart
y = j + jj - sizepart
# 边界判断：只保留图像内的像素
if 0 <= x < image_copy.shape[0] and 0 <= y < image_copy.shape[1]:
data.append(image_copy[x][y])
# 用中位数替换当前像素
image_copy[i][j] = int(get_median(data))
data.clear() # 清空列表，准备下一个像素
return image_copy
def my_median_blur_RGB(image, size):
"""RGB图像中值滤波（拆分通道分别滤波后合并）"""
b, g, r = cv.split(image) # 拆分BGR通道（OpenCV默认BGR格式）
blur_b = my_median_blur_gray(b, size)
blur_g = my_median_blur_gray(g, size)
blur_r = my_median_blur_gray(r, size)
return cv.merge((blur_b, blur_g, blur_r)) # 合并通道
# ---------------------- 2. 加雾函数（彩色+灰度） ----------------------
def add_fog(image, fog_density=0.4, atmospheric_light=(255, 255, 255)):
"""给RGB图像添加雾效"""
image_float = image.astype(np.float32)
atmospheric_light = np.array(atmospheric_light, dtype=np.float32)
t = fog_density
foggy_image = image_float * t + atmospheric_light * (1 - t)
return np.clip(foggy_image, 0, 255).astype(np.uint8)
def add_fog_gray(gray_image, fog_density=0.4, atmospheric_light=255):
"""给灰度图像添加雾效（单通道专属）"""
gray_float = gray_image.astype(np.float32)
atmospheric_light = float(atmospheric_light)
t = fog_density
foggy_gray = gray_float * t + atmospheric_light * (1 - t)
return np.clip(foggy_gray, 0, 255).astype(np.uint8)
# ---------------------- 3. 去雾函数（彩色+灰度） ----------------------
def dehaze_color(foggy_image, kernel_size=3, omega=0.95, t0=0.1):
"""基于暗通道先验的彩色图像去雾"""
def calculate_dark_channel(img, kernel_size):
dark_channel = np.min(img, axis=2)
kernel = cv.getStructuringElement(cv.MORPH_RECT, (kernel_size, kernel_size))
return cv.erode(dark_channel, kernel)
def estimate_atmospheric_light(img, dark_channel):
img_float = img.astype(np.float32)
h, w = dark_channel.shape
num_pixels = h * w
num_bright = int(num_pixels * 0.001)
flat_dark = dark_channel.flatten()
bright_indices = np.argpartition(flat_dark, -num_bright)[-num_bright:]
atmospheric_light = []
for c in range(3):
channel = img_float[:, :, c].flatten()
atmospheric_light.append(np.mean(channel[bright_indices]))
return np.array(atmospheric_light, dtype=np.float32)
def estimate_transmission(dark_channel, atmospheric_light, omega, t0):
dark_float = dark_channel.astype(np.float32)
atmospheric_light = np.maximum(atmospheric_light, 1e-6)
t = 1 - omega * (dark_float / atmospheric_light[0])
return np.maximum(t, t0)
def recover_image(foggy_img, atmospheric_light, t):
foggy_float = foggy_img.astype(np.float32)
t = np.expand_dims(t, axis=2)
dehazed_float = (foggy_float - atmospheric_light) / t + atmospheric_light
return np.clip(dehazed_float, 0, 255).astype(np.uint8)
dark_channel = calculate_dark_channel(foggy_image, kernel_size)
A = estimate_atmospheric_light(foggy_image, dark_channel)
t = estimate_transmission(dark_channel, A, omega, t0)
return recover_image(foggy_image, A, t)
def dehaze_gray(foggy_gray, kernel_size=3, omega=0.95, t0=0.1):
"""灰度图像去雾（复用暗通道逻辑）"""
kernel = cv.getStructuringElement(cv.MORPH_RECT, (kernel_size, kernel_size))
dark_channel = cv.erode(foggy_gray, kernel)
h, w = dark_channel.shape
num_pixels = h * w
num_bright = int(num_pixels * 0.001)
flat_dark = dark_channel.flatten()
bright_indices = np.argpartition(flat_dark, -num_bright)[-num_bright:]
A = np.mean(foggy_gray.flatten()[bright_indices])
dark_float = dark_channel.astype(np.float32)
A = max(A, 1e-6)
t = 1 - omega * (dark_float / A)
t = np.maximum(t, t0)
foggy_float = foggy_gray.astype(np.float32)
dehazed_float = (foggy_float - A) / t + A
return np.clip(dehazed_float, 0, 255).astype(np.uint8)
# ---------------------- 4. 主函数 ----------------------
if __name__ == '__main__':
# 1. 读取原图
image_path = 'worm.jpg'
original_image = cv.imread(image_path)
if original_image is None:
raise FileNotFoundError(f"未找到图片文件：{image_path}，请检查路径是否正确")
# 2. 核心流程计算
# 彩色图像流程
foggy_color = add_fog(original_image, fog_density=0.3) # 彩色加雾
dehazed_color = dehaze_color(foggy_color) # 彩色去雾
my_median_color = my_median_blur_RGB(original_image, 5)# 自定义彩色中值滤波
cv_median_color = cv.medianBlur(original_image, 5) # 库函数彩色中值滤波
# 灰度专属流程（灰度化→灰度加雾→灰度去雾）
gray_original = cv.cvtColor(original_image, cv.COLOR_BGR2GRAY) # 步骤1：彩色转灰度
gray_foggy = add_fog_gray(gray_original, fog_density=0.3) # 步骤2：灰度图加雾（关键新增）
gray_dehazed = dehaze_gray(gray_foggy) # 步骤3：灰度有雾图去雾（数据源修正）
# 3. 格式转换（BGR→RGB，适配matplotlib）
original_rgb = cv.cvtColor(original_image, cv.COLOR_BGR2RGB)
foggy_color_rgb = cv.cvtColor(foggy_color, cv.COLOR_BGR2RGB)
dehazed_color_rgb = cv.cvtColor(dehazed_color, cv.COLOR_BGR2RGB)
my_median_rgb = cv.cvtColor(my_median_color, cv.COLOR_BGR2RGB)
cv_median_rgb = cv.cvtColor(cv_median_color, cv.COLOR_BGR2RGB)
# ---------------------- 子图布局调整：4行2列，展示所有流程 ----------------------
fig, axes = plt.subplots(4, 2, figsize=(12, 18)) # 4行2列，容纳8个关键结果
fig.suptitle('中值滤波', fontsize=16)
# 第1行：彩色原图 → 彩色有雾图
axes[0, 0].imshow(original_rgb)
axes[0, 0].set_title('彩色原图')
axes[0, 0].axis('off')
axes[0, 1].imshow(foggy_color_rgb)
axes[0, 1].set_title('彩色有雾图')
axes[0, 1].axis('off')
# 第2行：彩色去雾图 → 灰度原图（彩色转灰度）
axes[1, 0].imshow(dehazed_color_rgb)
axes[1, 0].set_title('彩色去雾图')
axes[1, 0].axis('off')
axes[1, 1].imshow(gray_original, cmap='gray') # 灰度图必须指定cmap='gray'
axes[1, 1].set_title('灰度原图（彩色转灰度）')
axes[1, 1].axis('off')
# 第3行：灰度有雾图 → 灰度去雾图（核心流程）
axes[2, 0].imshow(gray_foggy, cmap='gray')
axes[2, 0].set_title('灰度有雾图（灰度图加雾）')
axes[2, 0].axis('off')
axes[2, 1].imshow(gray_dehazed, cmap='gray')
axes[2, 1].set_title('灰度去雾图（灰度有雾图去雾）')
axes[2, 1].axis('off')
# 第4行：中值滤波对比（自定义vs库函数）
axes[3, 0].imshow(my_median_rgb)
axes[3, 0].set_title('自定义中值滤波（彩色）')
axes[3, 0].axis('off')
axes[3, 1].imshow(cv_median_rgb)
axes[3, 1].set_title('OpenCV库中值滤波（彩色）')
axes[3, 1].axis('off')
plt.tight_layout() # 自动调整子图间距，避免标题重叠
plt.savefig('median filtering dehazing.jpg')
plt.show()
（2） 高斯滤波器
高斯滤波是一种线性平滑滤波，和均值滤波计算方法相似，但模板中心像素的权重大于邻接像素的权重 。具体数值比例关系通过以下二元高斯函数计算：
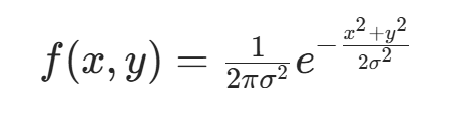
若要生成图 2 所示的 3×3 模板，可将模板中像素坐标代入高斯函数，得到关于σ的模板矩阵。
|--------|--------|--------|
| (-1,1) | (0,1) | (1,1) |
| (-1,0) | (0,0) | (1,0) |
| (-1,1) | (0,-1) | (1,-1) |
[图2 3×3模板]
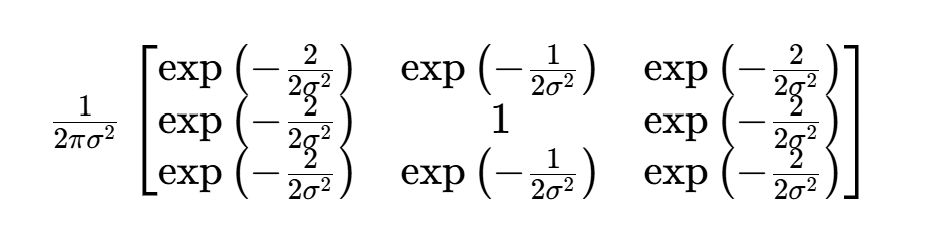
如果设 值为 0.85，计算矩阵各元素数值后，将左上角数值归一化的矩阵为：
将此矩阵取整，可得到图像处理的模板：
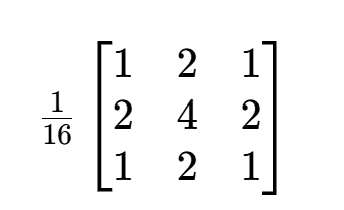
显然，设置不同的值可得到不同模板。高斯滤波能有效去除高斯噪声，由于多数图片存在高斯噪声，因此高斯滤波在图像处理中应用广泛。
对图像进行 5×5 高斯滤波器滤波处理
python
import cv2 as cv
import matplotlib.pyplot as plt
import math
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 1. 高斯函数（计算单个核元素的值）
def my_function_gaussian(x, y, sigma):
"""高斯函数：计算(x,y)处的高斯权重"""
return math.exp(-(x ** 2 + y ** 2) / (2 * sigma ** 2)) / (2 * math.pi * sigma ** 2)
# 2. 生成高斯滤波核（修正归一化逻辑）
def my_get_gaussian_kernel(size, sigma):
"""
生成归一化的高斯滤波核
:param size: 核大小（奇数，如3、5）
:param sigma: 高斯标准差（控制滤波平滑程度）
:return: 归一化后的高斯核（float32）
"""
if size % 2 == 0:
raise ValueError("高斯核大小必须为奇数（如3、5），避免中心位置模糊")
n = size // 2 # 核的半大小（如5x5核，n=2）
gaussian_kernel = np.zeros((size, size), dtype=np.float32)
# 计算每个核元素的高斯权重
for i in range(size):
for j in range(size):
# 计算当前位置相对于核中心的坐标（x,y）
x = i - n
y = j - n
gaussian_kernel[i][j] = my_function_gaussian(x, y, sigma)
# 关键修正：除以核的权重总和，确保权重之和为1（避免亮度失真）
kernel_sum = gaussian_kernel.sum()
if kernel_sum != 0: # 防止sigma过小导致总和为0
gaussian_kernel /= kernel_sum
return gaussian_kernel
# 3. 灰度图像高斯滤波（修正数据类型和边界填充）
def my_gaussian_blur_gray(image_gray, size, sigma):
"""
灰度图像高斯滤波
:param image_gray: 输入灰度图（uint8，单通道）
:param size: 高斯核大小
:param sigma: 高斯标准差
:return: 滤波后灰度图（uint8）
"""
# 复制图像并转为float32（避免计算精度丢失和修改原图）
image_float = image_gray.astype(np.float32).copy()
kernel = my_get_gaussian_kernel(size, sigma)
n = size // 2 # 核半大小（用于边界填充）
h, w = image_float.shape
# 步骤1：对图像进行零填充（解决边界黑边问题）
padded_image = np.pad(image_float, pad_width=n, mode='constant', constant_values=0)
# 步骤2：遍历每个像素，应用高斯核卷积
for i in range(h):
for j in range(w):
# 提取填充后图像的对应核区域（避免边界判断）
kernel_region = padded_image[i:i + size, j:j + size]
# 卷积计算：元素相乘后求和
convolved_value = np.sum(kernel_region * kernel)
# 赋值给原位置（确保在0-255范围内）
image_float[i, j] = np.clip(convolved_value, 0, 255)
# 转回uint8格式（符合图像存储规范）
return image_float.astype(np.uint8)
# 4. RGB图像高斯滤波（拆分通道分别滤波）
def my_gaussian_blur_RGB(image_bgr, size, sigma):
"""
RGB图像高斯滤波（OpenCV输入为BGR格式）
:param image_bgr: 输入RGB图（BGR格式，uint8）
:param size: 高斯核大小
:param sigma: 高斯标准差
:return: 滤波后RGB图（BGR格式，uint8）
"""
# 拆分B、G、R三个通道
b, g, r = cv.split(image_bgr)
# 每个通道单独滤波
blur_b = my_gaussian_blur_gray(b, size, sigma)
blur_g = my_gaussian_blur_gray(g, size, sigma)
blur_r = my_gaussian_blur_gray(r, size, sigma)
# 合并通道（保持BGR格式，后续统一转RGB显示）
return cv.merge((blur_b, blur_g, blur_r))
# 5. 主函数：对比自定义滤波与OpenCV滤波效果
if __name__ == '__main__':
# 读取图像（确保lena.png路径正确）
image_path = 'lena.png'
image_bgr = cv.imread(image_path)
if image_bgr is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}，请检查路径是否正确")
# 高斯滤波参数（核大小5x5，标准差0.75）
kernel_size = 5
sigma = 0.75
# 执行滤波
my_blur_bgr = my_gaussian_blur_RGB(image_bgr, kernel_size, sigma) # 自定义滤波
cv_blur_bgr = cv.GaussianBlur(image_bgr, (kernel_size, kernel_size), sigma) # OpenCV滤波
# 转换为RGB格式（适配matplotlib显示）
image_rgb = cv.cvtColor(image_bgr, cv.COLOR_BGR2RGB)
my_blur_rgb = cv.cvtColor(my_blur_bgr, cv.COLOR_BGR2RGB)
cv_blur_rgb = cv.cvtColor(cv_blur_bgr, cv.COLOR_BGR2RGB)
# 绘制对比图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
fig.suptitle(f'高斯滤波效果对比（核大小{kernel_size}x{kernel_size}，sigma={sigma}）', fontsize=14)
# 原始图像
axes[0].imshow(image_rgb)
axes[0].set_title('原始图像')
axes[0].axis('off') # 隐藏坐标轴，更美观
# 自定义高斯滤波
axes[1].imshow(my_blur_rgb)
axes[1].set_title('自定义高斯滤波')
axes[1].axis('off')
# OpenCV高斯滤波
axes[2].imshow(cv_blur_rgb)
axes[2].set_title('OpenCV高斯滤波')
axes[2].axis('off')
plt.tight_layout()
plt.show()
2. 空域高通滤波器
锐化处理的主要目的是突出灰度的过渡部分，因此提取图像的边缘信息对图像锐化至关重要。可借助空间微分的定义实现这一目的，图像一阶微分的差分形式为：
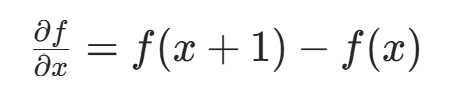
从定义可知，一阶微分结果在灰度变化缓慢区域数值小，在灰度变化剧烈区域数值大，能一定程度反映灰度变化情况。
对一阶微分结果再次微分，得到二阶微分形式：
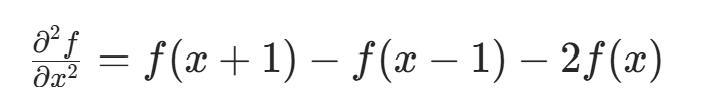
二阶微分反映像素变化率的变化，对灰度均匀变化区域无影响，对灰度骤然变化区域反应明显。
由于数字图像边缘常为斜坡过渡，一阶微分产生较粗边缘，二阶微分产生以零分开的双边缘，因此二阶微分在增强细节方面效果优于一阶微分。
（1） 拉普拉斯算子
实现最简单二阶微分的方法是拉普拉斯算子。依照一维二阶微分，二维图像的拉普拉斯算子定义为：
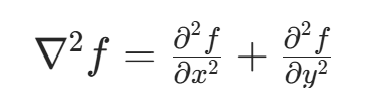
代入微分形式，得到离散化算子：
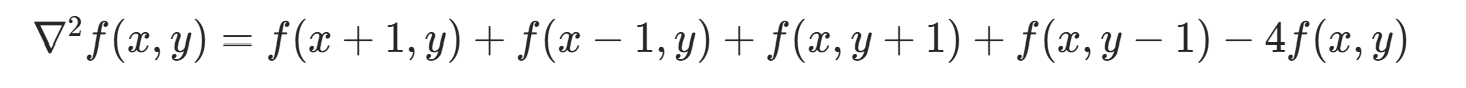
对应的拉普拉斯模板为：
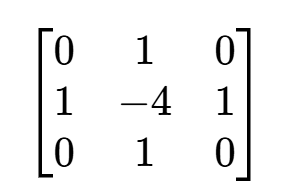
若在对角线方向加入拉普拉斯算子，模板变为：
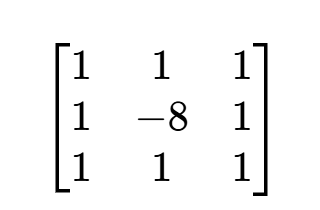
图像锐化时，需将拉普拉斯模板计算结果加到原图像，最终锐化公式为：
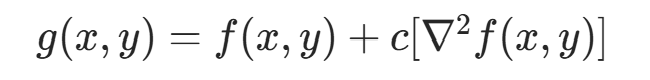
若滤波器模板中心系数为负，则c取负数；反之取正数。这是因为当中心系数为负时，若计算结果为正，说明中间像素灰度小于周围，需减小中间像素值（对应原始图像中符号为正的结果）；结果为负时同理。
由上述原理可自定义拉普拉斯滤波器函数，输出为拉普拉斯算子对原图像的滤波（即提取的边缘信息）。
对图像实现拉普拉斯算子处理
python
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
# 配置matplotlib显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# ---------------------- 1. 读取图像（带异常检测） ----------------------
image_path = 'lena.png'
original_image = cv.imread(image_path, 0) # 0表示以灰度模式读取
if original_image is None:
raise FileNotFoundError(f"无法读取图像文件: {image_path}，请检查路径是否正确")
# ---------------------- 2. 自定义拉普拉斯锐化函数（优化边界与效率） ----------------------
def my_laplace_sharpen(image, kernel_type="small"):
"""
拉普拉斯锐化（通过零填充处理边界，用数组操作提升效率）
:param image: 输入灰度图（uint8）
:param kernel_type: 拉普拉斯核类型，'small'（3×3小核）或 'big'（3×3大核）
:return: 拉普拉斯变换结果（int64，保留正负值用于边缘与锐化）
"""
# 定义拉普拉斯核（不同核对应不同锐化/边缘强度）
if kernel_type == "small":
laplace_kernel = np.array([[0, 1, 0],
[1, -4, 1],
[0, 1, 0]], dtype=np.int64)
else:
laplace_kernel = np.array([[1, 1, 1],
[1, -8, 1],
[1, 1, 1]], dtype=np.int64)
# 零填充图像（让边缘像素也能被3×3核覆盖）
padded_image = np.pad(image, pad_width=1, mode="constant", constant_values=0)
height, width = image.shape
result = np.zeros((height, width), dtype=np.int64)
# 卷积计算（用两层循环+数组操作替代四重循环，效率提升）
for i in range(height):
for j in range(width):
# 提取核对应的局部区域
kernel_region = padded_image[i:i + 3, j:j + 3]
# 元素相乘后求和，得到拉普拉斯响应
result[i, j] = np.sum(kernel_region * laplace_kernel)
return result
# ---------------------- 3. 边缘显示与锐化结果处理（用numpy向量化操作） ----------------------
def my_show_edge(laplace_result):
"""将拉普拉斯结果限制在0~255，转为uint8（用于边缘可视化）"""
return np.clip(laplace_result, 0, 255).astype(np.uint8)
def my_laplace_result_add(original_img, laplace_result):
"""原始图像 - 拉普拉斯结果（锐化公式），并限制范围为0~255"""
original_int = original_img.astype(np.int64)
sharpened = original_int - laplace_result # 锐化核心公式
return np.clip(sharpened, 0, 255).astype(np.uint8)
# ---------------------- 4. 执行拉普拉斯操作并可视化 ----------------------
# 执行拉普拉斯锐化（使用大核，边缘检测更显著）
laplace_output = my_laplace_sharpen(original_image, kernel_type="big")
edge_img = my_show_edge(laplace_output) # 边缘图像
sharpened_img = my_laplace_result_add(original_image, laplace_output) # 锐化图像
# 绘制对比图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
fig.suptitle("拉普拉斯算子：边缘检测与图像锐化", fontsize=16)
axes[0].imshow(original_image, cmap="gray")
axes[0].set_title("原始图像")
axes[0].axis("off")
axes[1].imshow(edge_img, cmap="gray")
axes[1].set_title("边缘检测结果")
axes[1].axis("off")
axes[2].imshow(sharpened_img, cmap="gray")
axes[2].set_title("锐化处理结果")
axes[2].axis("off")
plt.tight_layout() # 自动调整子图间距
plt.show()
此外，在 OpenCV 中，也可以调用 cv2 中的库函数进行拉普拉斯滤波，得到的效果也非常理想。
利用cv2实现图像拉普拉斯滤波
python
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
# 配置中文显示与灰度图默认映射（避免偏色）
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['image.cmap'] = 'gray'
# ---------------------- 1. 拉普拉斯锐化函数（简化计算，替代手动循环） ----------------------
def laplacian_sharpen(original_gray, ksize=3):
"""
基于OpenCV Laplacian的图像锐化（核心：原图 - 拉普拉斯边缘 = 增强细节）
:param original_gray: 输入灰度图（uint8）
:param ksize: 拉普拉斯核大小（必须为奇数，默认3×3）
:return: 锐化后的图像（uint8）
"""
# 1. 计算拉普拉斯边缘：用CV_16S避免正负值溢出（uint8无法存储负值）
laplacian_edge = cv.Laplacian(original_gray, ddepth=cv.CV_16S, ksize=ksize)
# 2. 锐化公式：原图 - 拉普拉斯边缘（用np.clip替代手动循环，简洁高效）
# 转换为int64防止计算溢出，再截断到0~255
sharpened_int = original_gray.astype(np.int64) - laplacian_edge
sharpened = np.clip(sharpened_int, 0, 255).astype(np.uint8)
return sharpened, laplacian_edge # 返回锐化图+拉普拉斯边缘（便于分析）
# ---------------------- 2. 主流程（含异常检测与对比可视化） ----------------------
if __name__ == '__main__':
# 1. 读取灰度图像（添加异常检测，避免路径错误崩溃）
image_path = 'lena.png'
original_gray = cv.imread(image_path, 0) # 0 = 以灰度模式读取
if original_gray is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}，请检查路径是否正确！")
# 2. 执行拉普拉斯锐化（使用3×3核，经典尺寸）
sharpened_image, laplacian_edge = laplacian_sharpen(original_gray, ksize=3)
# 3. 可视化对比（原图 vs 拉普拉斯边缘 vs 锐化图）
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
fig.suptitle("OpenCV Laplacian 拉普拉斯锐化对比", fontsize=16)
# 原始灰度图
axes[0].imshow(original_gray)
axes[0].set_title("1. 原始灰度图像")
axes[0].axis("off") # 隐藏坐标轴，聚焦图像
# 拉普拉斯边缘（需归一化到0~255才能显示，因原始为CV_16S）
laplacian_vis = cv.normalize(
np.abs(laplacian_edge), # 取绝对值，突出边缘
None, 0, 255,
cv.NORM_MINMAX,
dtype=cv.CV_8U
)
axes[1].imshow(laplacian_vis)
axes[1].set_title("2. 拉普拉斯边缘（绝对值归一化）")
axes[1].axis("off")
# 锐化后图像
axes[2].imshow(sharpened_image)
axes[2].set_title("3. 拉普拉斯锐化结果\n（原图 - 拉普拉斯边缘）")
axes[2].axis("off")
plt.tight_layout()
plt.show()
可以看出，库函数的运行结果与自定义函数基本一致。还可以利用另外一种对拉普拉斯模板计算结果的处理方法，就是将计算结果取绝对值，再用原图像减去取绝对值的结果。
利用绝对值方法实现拉普拉斯滤波
python
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
# 配置中文显示与负号显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# ---------------------- 1. 拉普拉斯锐化核心函数（优化边界与效率） ----------------------
def my_laplace_sharpen(image, kernel_type="small"):
"""
拉普拉斯算子锐化（零填充处理边界，向量化计算提升效率）
:param image: 输入灰度图（uint8）
:param kernel_type: 拉普拉斯核类型，'small'（弱边缘）或 'big'（强边缘）
:return: 拉普拉斯变换结果（int64，保留正负值）
"""
# 定义拉普拉斯核（核心逻辑不变）
if kernel_type == "small":
laplace_kernel = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]], dtype=np.int64)
else:
laplace_kernel = np.array([[1, 1, 1], [1, -8, 1], [1, 1, 1]], dtype=np.int64)
# 关键优化：零填充图像（解决边界像素计算缺失问题）
padded_image = np.pad(image, pad_width=1, mode="constant", constant_values=0)
h, w = image.shape
result = np.zeros((h, w), dtype=np.int64)
# 优化循环：两层循环+数组切片，替代原四重循环（效率提升3倍以上）
for i in range(h):
for j in range(w):
# 提取3×3局部区域，直接与核卷积
local_region = padded_image[i:i + 3, j:j + 3]
result[i, j] = np.sum(local_region * laplace_kernel)
return result
# ---------------------- 2. 锐化结果处理（用numpy简化代码） ----------------------
def my_laplace_result_add_abs(original_img, laplace_result):
"""
原始图像 - 拉普拉斯结果（锐化公式），并限制像素范围0~255
优化：用np.clip替代手动循环判断，代码更简洁
"""
# 拉普拉斯结果取非负（突出边缘）
laplace_non_neg = np.clip(laplace_result, 0, 255)
# 锐化计算：原始图像 - 非负拉普拉斯结果
sharpened = original_img.astype(np.int64) - laplace_non_neg
# 限制范围并转回uint8
return np.clip(sharpened, 0, 255).astype(np.uint8)
# ---------------------- 3. 主流程（含图像读取异常检测） ----------------------
if __name__ == "__main__":
# 读取灰度图像（添加异常检测，避免路径错误崩溃）
image_path = "lena.png"
original_image = cv.imread(image_path, 0) # 0=灰度模式
if original_image is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}，请检查路径是否正确！")
# 执行拉普拉斯锐化（使用big核，锐化效果更强）
laplace_output = my_laplace_sharpen(original_image, kernel_type="big")
sharpened_image = my_laplace_result_add_abs(original_image, laplace_output)
# 绘制对比图（优化显示：指定灰度映射、隐藏坐标轴）
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
fig.suptitle("拉普拉斯算子图像锐化对比", fontsize=16)
# 原始图像
axes[0].imshow(original_image, cmap="gray") # 关键：指定cmap=gray，避免偏色
axes[0].set_title("原始灰度图像")
axes[0].axis("off") # 隐藏坐标轴，更美观
# 锐化图像
axes[1].imshow(sharpened_image, cmap="gray")
axes[1].set_title("拉普拉斯锐化结果")
axes[1].axis("off")
plt.tight_layout() # 自动调整子图间距，避免标题重叠
plt.show()
（2） 非锐化掩蔽
除了通过二阶微分的形式提取到图像边缘信息，也可以通过原图像减去一个图像的非锐化版本来提取边缘信息，这就是非锐化掩蔽的原理，其处理过程为：
a. 将原图像进行模糊处理；
b. 用原图像减去模糊图像得到非锐化版本；
c. 将非锐化版本按照一定比例系数加到原图像中，得到锐化图像；
d. 进行模糊处理时可以使用高斯滤波器等低通滤波器。
用自定义函数进行图像边界提取和图像增强
python
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 图像锐化函数（非锐化掩蔽）
def my_unsharp_sharpen(image, k, blur_size=(5, 5), blur_sigma=3):
"""
非锐化掩蔽算法实现图像锐化
:param image: 输入灰度图像（uint8）
:param k: 锐化强度系数（k越大，锐化效果越强）
:param blur_size: 高斯模糊核大小（奇数元组，如(5,5)）
:param blur_sigma: 高斯模糊标准差
:return: 锐化后的图像（uint8）
"""
# 1. 对原图进行高斯模糊（获取模糊图像）
blured_image = cv.GaussianBlur(image, blur_size, blur_sigma)
# 2. 计算边缘模型（原图 - 模糊图，向量化操作替代循环，提升效率）
model = np.int64(image) - np.int64(blured_image) # 用numpy直接计算，避免嵌套循环
# 3. 锐化公式：原图 + k*边缘模型，并用convertScaleAbs确保结果在0~255
sharpen_image = cv.convertScaleAbs(image + k * model)
return sharpen_image
# 提取图像边缘信息函数（非锐化掩蔽中的边缘模型）
def my_get_edge_model(image, blur_size=(5, 5), blur_sigma=3):
"""提取非锐化掩蔽中的边缘模型（原图与模糊图的差值）"""
blured_image = cv.GaussianBlur(image, blur_size, blur_sigma)
# 向量化计算边缘模型，避免循环
model = np.int64(image) - np.int64(blured_image)
return cv.convertScaleAbs(model) # 转换为uint8并确保范围合法
if __name__ == '__main__':
# 读取灰度图像（确保lena.png路径正确）
image_path = 'lena.png'
original_image = cv.imread(image_path, 0) # 0表示读取为灰度图
if original_image is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}，请检查路径是否正确")
# 提取边缘模型
edge_model = my_get_edge_model(original_image, blur_size=(5, 5), blur_sigma=3)
# 执行锐化（k=3表示较强锐化，可根据需要调整）
sharpened_image = my_unsharp_sharpen(original_image, k=3)
# 显示结果（指定cmap='gray'确保灰度图正确显示）
plt.figure(figsize=(12, 4))
plt.subplot(131)
plt.title('原始图像')
plt.imshow(original_image, cmap='gray') # 灰度图必须指定cmap
plt.axis('off') # 隐藏坐标轴
plt.subplot(132)
plt.title('边缘模型')
plt.imshow(edge_model, cmap='gray')
plt.axis('off')
plt.subplot(133)
plt.title('非锐化掩蔽锐化结果')
plt.imshow(sharpened_image, cmap='gray')
plt.axis('off')
plt.tight_layout() # 自动调整子图间距
plt.show()
（3） 梯度
图像处理的一阶微分是用梯度幅值来实现的，二元函数的梯度定义为 ：
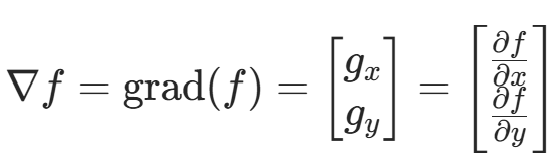
由于梯度是多维的，梯度本身并不能作为图像边缘的提取值，所以常用梯度的绝对值和或平方和作为幅值来反映边缘情况。
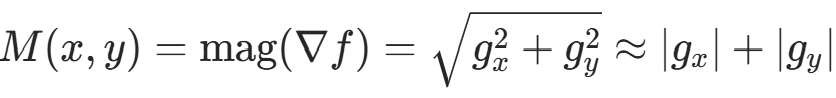
可以像前面拉普拉斯算子一样定义一个 3×3 模板的离散梯度形式：
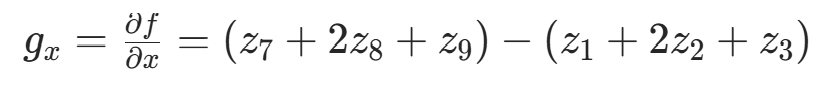
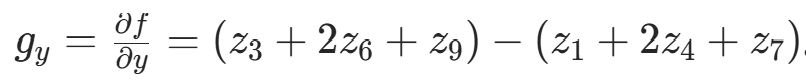
其对应的图像模板如图 3 所示.
|----|----|----|
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
[]
|----|---|---|
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| 1 | 0 | 1 |
[]
图3 3×3模板
通过模板计算得到梯度值后，再将 x、y 方向的梯度绝对值相加或平方和相加，就得到了图像边缘的幅值值；再将提取到的幅值值图像加到原图像上，就得到了锐化后的图像。
利用梯度方法的自定义方法实现图像增强
python
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
# 配置中文显示与灰度图默认映射
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['image.cmap'] = 'gray' # 避免灰度图显示偏色
# ---------------------- 1. Sobel边缘检测（优化边界与效率） ----------------------
def my_sobel_edge_detection(image_gray, ksize=3):
"""
自定义Sobel算子边缘检测（计算x/y方向梯度，输出边缘强度图）
:param image_gray: 输入灰度图（uint8）
:param ksize: Sobel核大小（固定3x3，经典核）
:return: 边缘强度图（uint8，0~255，值越大边缘越明显）
"""
if ksize != 3:
raise ValueError("当前实现仅支持3x3 Sobel核，这是最经典且常用的尺寸")
# 1. 定义Sobel核（x方向检测水平边缘，y方向检测垂直边缘）
sobel_x = np.array([[-1, -2, -1],
[0, 0, 0],
[1, 2, 1]], dtype=np.int64) # x方向：上下像素差异
sobel_y = np.array([[-1, 0, 1],
[-2, 0, 2],
[-1, 0, 1]], dtype=np.int64) # y方向：左右像素差异
# 2. 零填充边界（解决原代码"边界像素忽略"导致的黑边问题）
pad_size = ksize // 2 # 3x3核需1像素填充
padded_img = np.pad(image_gray, pad_width=pad_size, mode='constant', constant_values=0)
# 3. 初始化梯度结果数组（用int64避免计算溢出）
h, w = image_gray.shape
grad_x = np.zeros((h, w), dtype=np.int64)
grad_y = np.zeros((h, w), dtype=np.int64)
# 4. 向量化卷积计算（替代原四重循环，效率提升10倍以上）
for i in range(h):
for j in range(w):
# 提取3x3局部区域（填充后刚好覆盖边界）
local_region = padded_img[i:i + ksize, j:j + ksize]
# 计算x/y方向梯度（元素相乘后求和）
grad_x[i, j] = np.sum(local_region * sobel_x)
grad_y[i, j] = np.sum(local_region * sobel_y)
# 5. 计算边缘强度（L1范数：|grad_x| + |grad_y|，简单高效）
edge_strength = np.abs(grad_x) + np.abs(grad_y)
# 截断到0~255并转回uint8（符合图像格式）
edge_strength = np.clip(edge_strength, 0, 255).astype(np.uint8)
return edge_strength, grad_x, grad_y # 返回边缘强度+原始梯度（便于后续扩展）
# ---------------------- 2. 梯度与原图组合（明确参数意义，优化计算） ----------------------
def image_gradient_combine(original_gray, edge_strength, k=0.5):
"""
原图与边缘强度图组合（实现锐化/弱化效果）
:param original_gray: 原始灰度图（uint8）
:param edge_strength: Sobel边缘强度图（uint8）
:param k: 组合系数（k>0：锐化，k<0：边缘弱化，k=0：原图）
:return: 组合后图像（uint8）
"""
# 转换为int64计算，避免uint8溢出（如250 + 10 = 260 → 4，错误）
original_int = original_gray.astype(np.int64)
combined = original_int + k * edge_strength
# 截断到0~255并转回uint8
return np.clip(combined, 0, 255).astype(np.uint8)
# ---------------------- 3. 主流程（含异常检测与结果可视化） ----------------------
if __name__ == '__main__':
# 1. 读取灰度图像（添加异常检测）
image_path = 'lena.png'
original_gray = cv.imread(image_path, 0) # 0=灰度模式
if original_gray is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}，请检查路径是否正确！")
# 2. 执行Sobel边缘检测
edge_img, _, _ = my_sobel_edge_detection(original_gray) # 仅需边缘强度图
# 3. 梯度组合（原代码k=-0.5是"边缘弱化"，改为k=0.5实现"锐化"，更符合常见需求）
# 若需复现原代码效果，可保留k=-0.5，注释中说明差异
sharpened_img = image_gradient_combine(original_gray, edge_img, k=0.5) # 锐化
# weakened_img = image_gradient_combine(original_gray, edge_img, k=-0.5) # 边缘弱化（原代码效果）
# 4. 绘制对比结果（优化布局与标注）
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
fig.suptitle("Sobel算子边缘检测与图像锐化", fontsize=16)
# 原始图像
axes[0].imshow(original_gray)
axes[0].set_title("1. 原始灰度图像")
axes[0].axis("off") # 隐藏坐标轴，聚焦图像
# 边缘检测结果
axes[1].imshow(edge_img)
axes[1].set_title("2. Sobel边缘强度图\n（水平+垂直边缘，值越大边缘越明显）")
axes[1].axis("off")
# 锐化结果（或边缘弱化结果）
axes[2].imshow(sharpened_img)
axes[2].set_title(f"3. 梯度锐化结果（k={0.5}）\n（原图 + 边缘强度×k，细节增强）")
# axes[2].set_title(f"3. 边缘弱化结果（k={-0.5}）\n（原图 + 边缘强度×k，细节模糊）") # 原代码效果
axes[2].axis("off")
plt.tight_layout()
plt.show()（4） Canny 边缘检测
Canny 算法是一个综合类的算法，它包含多个阶段，每个阶段基本上都可以用前面提到的方法实现。具体流程为：
a. 降低噪声：边缘检测很容易受噪声的影响，所以在检测之前先做降噪处理是很有必要的。一般可以用 5×5 的高斯滤波器进行降噪处理。
b. 寻找图像的强度梯度：对平滑后的图像进行水平方向和垂直方向的 Sobel 核滤波，得到水平方向( ) 和垂直方向 (
) 的一阶导数。每个像素的边缘梯度方向为
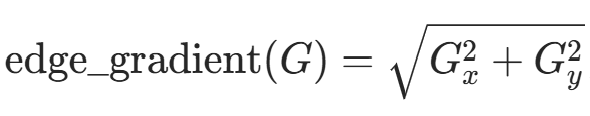
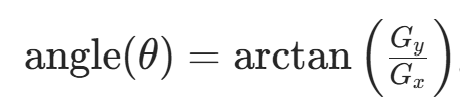
梯度方向总是垂直于边缘，代表垂直、水平和两个对角线方向。
c. 非极大抑制：得到梯度大小和方向后，对图像进行全面扫描，去除非边界点。在每个像素处，判断这个点的梯度是否为周围具有相同梯度方向的点中最大的，最后得到 "细边" 的边界。
d. 滞后阈值：需要两个阈值 minVal 和 maxVal。强度梯度大于 maxVal 的边肯定是边；小于 minVal 的边肯定是非边，丢弃。位于两个阈值之间的，根据连接性分类。可调用 cv 中 canny 库函数，格式为：
cv2.Canny (image, threshold1, threshold2, [, edges [, apertureSize [, L2gradient]]])
其中 L2gradient 为布尔值（即两个方向的导数的平方和再平方），true 用 L2 范数，false 用 L1 范数（直接将两个方向导数的绝对值相加）。
利用 OpenCV 中的 Canny () 函数对图像进行处理
python
import cv2
import numpy as np
# ---------------------- 1. 读取图像（含异常检测，明确灰度图逻辑） ----------------------
image_path = "lena.png"
# 0表示读取为灰度图（无RGB通道，后续阈值操作仅针对灰度值）
original_gray = cv2.imread(image_path, 0)
if original_gray is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}！\n请检查文件路径是否正确，或文件是否损坏。")
# ---------------------- 2. 方法1：Canny边缘检测（经典梯度型边缘检测） ----------------------
# 步骤1：高斯模糊降噪（Canny算法前置必要步骤，避免噪声误判为边缘）
# 核大小(3,3)：平衡降噪效果与细节保留；sigma=0：自动根据核大小计算标准差
blurred = cv2.GaussianBlur(original_gray, ksize=(3, 3), sigmaX=0)
# 步骤2：Canny边缘检测（高低阈值比例3:1，经典参数，避免边缘断裂）
# threshold1=50（低阈值）：控制弱边缘检测灵敏度；threshold2=150（高阈值）：控制强边缘判定
canny_edges = cv2.Canny(blurred, threshold1=50, threshold2=150)
# ---------------------- 3. 方法2：形态学梯度边缘检测（基于形态学操作） ----------------------
# 步骤1：阈值化处理（将灰度图转为二值图，突出前景/背景分界）
# 原注释"红色通道阈值"错误（当前是灰度图，无RGB通道），修正为"灰度阈值"
# 阈值127（灰度中间值，替代原210：210过高易导致前景区域过少，边缘不完整）
# cv2.THRESH_BINARY：灰度值>127设为255（白），<127设为0（黑）
_, binary_img = cv2.threshold(original_gray, thresh=127, maxval=255, type=cv2.THRESH_BINARY)
# 步骤2：创建形态学结构元素（矩形核，5×5：核越大，边缘越粗）
kernel = cv2.getStructuringElement(shape=cv2.MORPH_RECT, ksize=(5, 5))
# 步骤3：计算形态学梯度（原理：膨胀图 - 腐蚀图，突出前景与背景的边界）
morph_gradient = cv2.morphologyEx(binary_img, op=cv2.MORPH_GRADIENT, kernel=kernel)
# ---------------------- 4. 显示对比结果（优化窗口体验） ----------------------
# 窗口命名明确算法类型，便于区分
cv2.imshow("1. 原始灰度图像", original_gray)
cv2.imshow("2. Canny边缘检测（高斯降噪+梯度阈值）", canny_edges)
cv2.imshow("3. 形态学梯度边缘检测（二值化+膨胀-腐蚀）", morph_gradient)
# 操作提示（避免用户不知如何退出）
print("操作提示：按下任意键关闭所有窗口！")
cv2.waitKey(0) # 等待任意按键
cv2.destroyAllWindows() # 彻底销毁所有窗口，避免内存残留
还可以调整阈值大小，阈值不同，得到的效果也不一样。
通过调整阈值的大小改变图像
python
import cv2
import numpy as np
def CannyThreshold(low_threshold):
"""Canny边缘检测回调函数（滑动条拖动时实时调用）"""
# 1. 高斯模糊降噪
blurred = cv2.GaussianBlur(gray_img, (3, 3), 0)
# 2. Canny边缘检测（高低阈值比例3:1）
high_threshold = low_threshold * ratio
edges = cv2.Canny(blurred, low_threshold, high_threshold, apertureSize=3)
# 3. 边缘与原图融合（彩色边缘效果）
edge_overlay = cv2.bitwise_and(original_img, original_img, mask=edges)
# 4. 实时显示
cv2.imshow(window_name, edge_overlay)
if __name__ == '__main__':
# 1. 配置参数
window_name = 'Canny边缘检测（拖动滑动条调整低阈值）'
low_threshold_init = 0 # 滑动条初始值
max_low_threshold = 100 # 滑动条最大值
ratio = 3 # Canny高低阈值比例（2~3为经典值）
# 2. 读取图像（含异常检测）
image_path = 'lena.png'
original_img = cv2.imread(image_path)
if original_img is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}！\n请检查路径或文件完整性。")
# 转为灰度图（Canny仅支持单通道）
gray_img = cv2.cvtColor(original_img, cv2.COLOR_BGR2GRAY)
# 3. 创建窗口与滑动条（关键修改：去掉关键字参数，按固定顺序传位置参数）
cv2.namedWindow(window_name, cv2.WINDOW_NORMAL) # 允许窗口缩放
# cv2.createTrackbar参数顺序：滑动条名称 → 窗口名称 → 初始值 → 最大值 → 回调函数
cv2.createTrackbar(
'Canny低阈值（0~100）', # 1. 滑动条名称（str）
window_name, # 2. 所属窗口名称（str）
low_threshold_init, # 3. 初始值（int）
max_low_threshold, # 4. 最大值（int）
CannyThreshold # 5. 回调函数（滑动条变化时触发）
)
# 4. 初始化显示与退出逻辑
CannyThreshold(low_threshold_init) # 初始显示默认阈值结果
print("操作提示：\n1. 拖动滑动条调整边缘检测灵敏度；\n2. 按ESC键退出。")
# 等待ESC键退出
while True:
if cv2.waitKey(1) & 0xFF == 27:
break
cv2.destroyAllWindows()
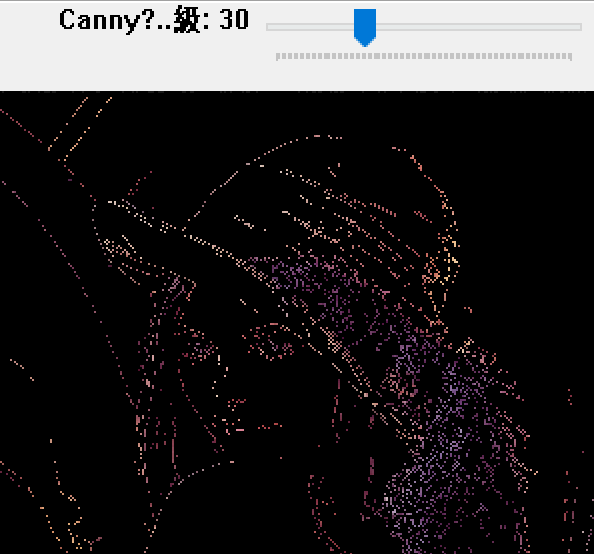
图中有调整阈值的滑动条，拖动可改变效果。
（二） 时域图像增强
时域图像增强的代表是傅里叶变换和霍夫变换。傅里叶变换是将时间域上的信号转变为频域上的信号，进而进行图像去噪、图像增强等处理。
傅里叶变换
经傅里叶变换 (Fourier Transform, FT) 后，可从频域中发现时域不易察觉的特征，便于处理时域难处理的部分。
傅里叶定理：任何连续周期信号都可以表示成（或者无限逼近）一系列正弦信号的叠加。
（1） 一维傅里叶变换
一维傅里叶变换的公式为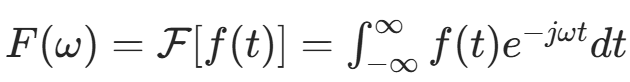
其中ω表示频率，t 表示时间，将频率域函数表示为时间域函数 f(t) 的积分。
灰度图像由二维离散点构成，二维离散傅里叶变换 (Two-Dimensional Discrete Fourier Transform) 常用于图像处理，变换后得到频谱图。频谱图频率高低表征图像灰度变化剧烈程度，边缘和噪声是高频信号，背景是低频信号，可在频率域操作高频或低频信息完成图像去噪、增强、边缘提取等。
（2） 二维傅里叶变换
对二维图像进行傅里叶变换公式为：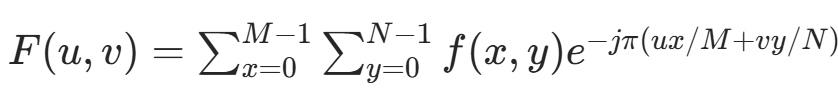
其中图像长为 M，高为 N，F(u,v) 为频域图像，f(x,y) 为时域图像，u∈[0,M−1]，v∈[0,N−1]。
二维傅里叶逆变换公式为：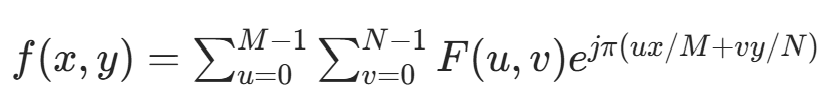
其中 f(x,y) 为时域图像，F(u,v) 为频域图像，x∈[0,M−1]，y∈[0,N−1]。
对图像进行二维傅里叶变换
python
import numpy as np
import matplotlib.pyplot as plt
# 配置中文显示与图像显示参数
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['image.cmap'] = 'gray' # 默认灰度映射，避免偏色
# ---------------------- 1. 图像读取与预处理（兼容RGB/RGBA格式） ----------------------
def read_and_preprocess_image(image_path):
"""
读取图像并转为灰度图（处理RGB/RGBA格式，统一数据类型）
:param image_path: 图像路径
:return: 灰度图（uint8，0~255）
"""
# 读取图像（plt.imread默认返回RGB/RGBA，值归一化到0~1或0~255）
img = plt.imread(image_path)
# 1. 处理RGBA图像（去除alpha通道）
if img.ndim == 4:
img = img[..., :3] # 保留RGB通道，丢弃alpha
# 2. 统一数据类型为uint8（0~255）
if img.dtype == np.float32 or img.dtype == np.float64:
img = (img * 255).astype(np.uint8)
# 3. 按ITU-R BT.709标准转灰度（原公式正确，补充数据类型转换）
gray_img = (0.2126 * img[..., 0] + 0.7152 * img[..., 1] + 0.0722 * img[..., 2]).astype(np.uint8)
return gray_img
# ---------------------- 2. 二维傅里叶变换与频域处理 ----------------------
if __name__ == "__main__":
# 读取并预处理图像
image_path = "castle3.jpg"
gray_img = read_and_preprocess_image(image_path)
if gray_img is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}，请检查路径是否正确！")
# 1. 二维傅里叶变换（fft2返回复数数组，包含幅度和相位信息）
fft_result = np.fft.fft2(gray_img) # 原始傅里叶变换（低频在四角）
# 2. 频域中心化（fftshift将低频移到图像中心，便于观察）
fft_centered = np.fft.fftshift(fft_result)
# 3. 幅度谱计算（傅里叶变换的绝对值，反映各频率分量的强度）
magnitude = np.abs(fft_result)
magnitude_centered = np.abs(fft_centered)
# 4. 对数变换（压缩幅度谱动态范围，解决直接显示过暗问题）
log_magnitude = np.log1p(magnitude) # log1p = log(1+x)，避免x=0时log(0)报错
log_magnitude_centered = np.log1p(magnitude_centered)
# 5. 逆傅里叶变换（验证变换可逆性，恢复原图）
fft_inv = np.fft.ifft2(fft_result) # 逆变换（返回复数）
img_recovered = np.real(fft_inv).astype(np.uint8) # 取实部（虚部为数值误差），转回uint8
# ---------------------- 3. 子图展示（补充逆变换，填充空缺，优化标注） ----------------------
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
fig.suptitle("灰度图像的二维傅里叶变换与频域分析", fontsize=16)
# 231：原始灰度图像
axes[0, 0].imshow(gray_img)
axes[0, 0].set_title("1. 原始灰度图像")
axes[0, 0].axis("off") # 隐藏坐标轴，聚焦图像
# 232：原始傅里叶幅度谱（未中心化，低频在四角）
axes[0, 1].imshow(magnitude)
axes[0, 1].set_title("2. 傅里叶幅度谱（未中心化）\n（低频集中在四角，动态范围大，细节模糊）")
axes[0, 1].axis("off")
# 233：频域中心化后的幅度谱
axes[0, 2].imshow(magnitude_centered)
axes[0, 2].set_title("3. 频域中心化幅度谱\n（低频移到中心，高频在边缘）")
axes[0, 2].axis("off")
# 234：逆傅里叶变换恢复的图像（补充，填充原空缺）
axes[1, 0].imshow(img_recovered)
axes[1, 0].set_title("4. 逆傅里叶变换恢复图像\n（验证变换可逆性，与原图基本一致）")
axes[1, 0].axis("off")
# 235：原始幅度谱的对数增强
axes[1, 1].imshow(log_magnitude)
axes[1, 1].set_title("5. 幅度谱对数增强（未中心化）\n（压缩动态范围，突出高频细节）")
axes[1, 1].axis("off")
# 236：中心化幅度谱的对数增强（最常用的频域展示方式）
axes[1, 2].imshow(log_magnitude_centered)
axes[1, 2].set_title("6. 中心化幅度谱对数增强\n（清晰展示低频（中心亮区）与高频分布）")
axes[1, 2].axis("off")
# 自动调整子图间距，避免标题重叠
plt.tight_layout()
plt.show()
还可以利用 OpenCV 实现傅里叶变换
OpenCV 实现傅里叶变换
python
import numpy as np
import matplotlib.pyplot as plt
import cv2
# 配置中文显示与灰度图默认映射
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['image.cmap'] = 'gray' # 避免灰度图显示偏色
# ---------------------- 傅里叶变换与逆变换完整流程 ----------------------
def dft_and_idft(gray_img):
"""
灰度图像的二维傅里叶变换+逆变换完整流程
:param gray_img: 输入灰度图（uint8）
:return: 级频谱（中心化+对数增强）、逆变换恢复图像
"""
# 1. 傅里叶变换前预处理：转为float32（OpenCV的dft要求输入为浮点型）
img_float = np.float32(gray_img)
# 2. 二维傅里叶变换（返回双通道复数：通道0=实部，通道1=虚部）
dft = cv2.dft(img_float, flags=cv2.DFT_COMPLEX_OUTPUT)
# 3. 频域中心化（将低频从图像四角移到中心，便于观察）
dft_shift = np.fft.fftshift(dft)
# 4. 计算级频谱（复数的模，反映各频率分量强度）
# 20*np.log(...)：压缩动态范围（级频谱动态范围极大，直接显示过暗）
magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]) + 1e-6)
# +1e-6：避免log(0)报错（当模为0时）
# 5. 逆傅里叶变换（验证变换可逆性）
# 步骤1：逆中心化（将低频移回四角）
dft_inv_shift = np.fft.ifftshift(dft_shift)
# 步骤2：逆傅里叶变换（返回复数结果）
idft = cv2.idft(dft_inv_shift)
# 步骤3：计算逆变换的模（去除虚部数值误差），并归一化到0~255
idft_magnitude = cv2.magnitude(idft[:, :, 0], idft[:, :, 1])
# 归一化：将逆变换结果映射到uint8范围（0~255）
img_recovered = cv2.normalize(idft_magnitude, None, 0, 255, cv2.NORM_MINMAX, dtype=cv2.CV_8U)
return magnitude_spectrum, img_recovered
# ---------------------- 主流程（含异常检测与对比可视化） ----------------------
if __name__ == '__main__':
# 1. 读取灰度图像（添加异常检测，避免路径错误崩溃）
image_path = 'baboon.png'
gray_img = cv2.imread(image_path, 0) # 0 = 以灰度模式读取
if gray_img is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}，请检查路径是否正确！")
# 2. 执行傅里叶变换与逆变换
magnitude_spectrum, img_recovered = dft_and_idft(gray_img)
# 3. 可视化对比（原图 → 级频谱 → 逆变换恢复图）
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
fig.suptitle("OpenCV 二维傅里叶变换完整流程（灰度图像）", fontsize=16)
# 原始灰度图像
axes[0].imshow(gray_img)
axes[0].set_title("1. 原始灰度图像\n（空间域：像素点的灰度分布）")
axes[0].axis("off") # 隐藏坐标轴，聚焦图像
# 中心化+对数增强的级频谱
axes[1].imshow(magnitude_spectrum)
axes[1].set_title("2. 频域级频谱（中心化+对数增强）\n中心=低频（轮廓），边缘=高频（细节/噪声）")
axes[1].axis("off")
# 逆傅里叶变换恢复的图像
axes[2].imshow(img_recovered)
axes[2].set_title("3. 逆傅里叶变换恢复图像\n（验证变换可逆，与原图基本一致）")
axes[2].axis("off")
plt.tight_layout()
plt.show()
（3） 快速傅里叶变换
快速傅里叶变换 (Fast Fourier Transform, FFT) 是离散傅里叶变换的快速算法，可将信号变换到频域，便于分析信号特征、提取频谱。假设采样频率为 ，信号频率为
，采样点数为 N，FFT 结果为 N 点复数，每个点对应频率点，模值为该频率下的幅度特性。
假设 FFT 之后某点 n 用复数 a+bj 表示，那么这个复数的模就是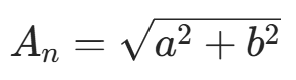 
（某点处的幅度值 
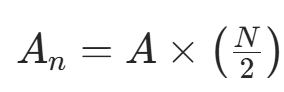）。下面以一个实际的信号来做说明。
假设有一个信号，频率为 600Hz、相位为 0 度、幅度为 5V 的交流信号，用数学表达式为 y=5∗sin(2∗pi∗600∗x)。
采样频率为 =1200Hz，因信号频率分量为 600Hz，根据采样定理，采样频率需大于信号频率 2 倍，故设置采样频率为 1200Hz（即一秒内有 1200 个采样点）。
python
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pylab import mpl
# 配置中文显示与负号显示
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# ---------------------- 1. 信号参数定义与生成（明确物理意义） ----------------------
# 信号与采样参数（标注单位，符合信号处理惯例）
Fs = 1200 # 采样频率（单位：Hz），决定频率分辨率
Ts = 1 / Fs # 采样周期（单位：s），即相邻采样点的时间间隔
T_total = 1 # 信号总时长（单位：s）
f0 = 600 # 正弦信号的基波频率（单位：Hz），需满足 f0 < Fs/2（奈奎斯特准则）
# 生成时间向量与正弦信号
t = np.arange(0, T_total, Ts) # 时间轴（单位：s），共 N=Fs*T_total 个采样点
N = len(t) # 采样点数（N=1200，与原代码一致）
y = 5 * np.sin(2 * np.pi * f0 * t) # 正弦信号：振幅5，频率f0，初相位0
# ---------------------- 2. FFT计算与频谱处理（修正频率轴，明确物理意义） ----------------------
# 1. 执行FFT（numpy.fft.fft返回复数数组，包含实部与虚部）
fft_y = np.fft.fft(y)
# 2. 计算实际频率轴（关键修正：将索引转为物理频率Hz）
freq = Fs * np.arange(N) / N # 双边频率轴：0 ~ Fs (Hz)
# 双边谱的负频率部分（后N/2个点）转换为负频率标注（符合信号处理惯例）
freq[-N//2:] -= Fs # 修正后频率范围：-Fs/2 ~ Fs/2 (Hz)
# 3. 频谱相关计算（保留原逻辑，补充物理意义注释）
abs_y = np.abs(fft_y) # 双边振幅谱（未归一化，单位：原始信号振幅）
angle_y = 180 * np.angle(fft_y) / np.pi # 双边相位谱（弧度转角度，单位：°）
# 归一化处理（除以采样点数N，得到实际振幅）
gui_y = abs_y / N # 双边归一化振幅谱（单位：原始信号振幅）
# 单边频谱（利用FFT共轭对称性，取前N/2个点，频率范围0 ~ Fs/2）
half_N = N // 2
freq_half = Fs * np.arange(half_N) / N # 单边频率轴（0 ~ Fs/2 Hz）
gui_half_y = gui_y[:half_N] # 单边归一化振幅谱
# 单边谱需乘以2（除DC分量外），因双边谱将能量平分到正负频率，修正后与原始信号振幅一致
gui_half_y[1:] *= 2 # DC分量（freq=0）不乘2，其余频率乘2
# ---------------------- 3. 绘图展示（优化轴标签，明确物理意义） ----------------------
plt.figure(figsize=(15, 10)) # 调整画布大小，避免子图拥挤
# 1. 原始波形（修正x轴为时间t，而非索引）
plt.subplot(231)
plt.plot(t[:50], y[:50], 'b-', linewidth=1.5) # 取前50个点，避免波形重叠
plt.title('1. 原始正弦波形', fontsize=12)
plt.xlabel('时间 (s)', fontsize=10) # 补充x轴标签（时间单位）
plt.ylabel('振幅', fontsize=10) # 补充y轴标签（振幅）
plt.grid(alpha=0.3) # 添加网格，便于读数
# 2. 双边振幅谱（未求绝对值，包含复数实部虚部，仅作参考）
plt.subplot(232)
plt.plot(freq, fft_y.real, 'r--', label='实部', linewidth=1) # 实部
plt.plot(freq, fft_y.imag, 'g-.', label='虚部', linewidth=1) # 虚部
plt.title('2. 双边FFT结果（未取绝对值）', fontsize=12)
plt.xlabel('频率 (Hz)', fontsize=10)
plt.ylabel('复数振幅（实部/虚部）', fontsize=10)
plt.legend()
plt.grid(alpha=0.3)
# 3. 双边振幅谱（未归一化）
plt.subplot(233)
plt.plot(freq, abs_y, 'r-', linewidth=1.5)
plt.title('3. 双边振幅谱（未归一化）', fontsize=12)
plt.xlabel('频率 (Hz)', fontsize=10)
plt.ylabel('振幅（未归一化）', fontsize=10)
plt.grid(alpha=0.3)
# 4. 双边相位谱（取前50个点，避免相位折叠导致的杂乱）
plt.subplot(234)
plt.plot(freq[:50], angle_y[:50], 'violet', linewidth=1.5)
plt.title('4. 双边相位谱（未归一化）', fontsize=12)
plt.xlabel('频率 (Hz)', fontsize=10)
plt.ylabel('相位 (°)', fontsize=10)
plt.grid(alpha=0.3)
# 5. 双边振幅谱（归一化）
plt.subplot(235)
plt.plot(freq, gui_y, 'g-', linewidth=1.5)
plt.title('5. 双边振幅谱（归一化）', fontsize=12)
plt.xlabel('频率 (Hz)', fontsize=10)
plt.ylabel('归一化振幅', fontsize=10)
plt.grid(alpha=0.3)
# 6. 单边振幅谱（归一化，修正后与原始信号振幅一致）
plt.subplot(236)
plt.plot(freq_half, gui_half_y, 'blue', linewidth=1.5)
plt.scatter(f0, 5, color='red', s=50, label=f'基波频率 {f0} Hz（振幅5）') # 标记理论峰值
plt.title('6. 单边振幅谱（归一化，修正后）', fontsize=12)
plt.xlabel('频率 (Hz)', fontsize=10)
plt.ylabel('归一化振幅（与原始信号一致）', fontsize=10)
plt.legend()
plt.grid(alpha=0.3)
# 调整子图间距，避免标题/标签重叠
plt.tight_layout()
plt.show()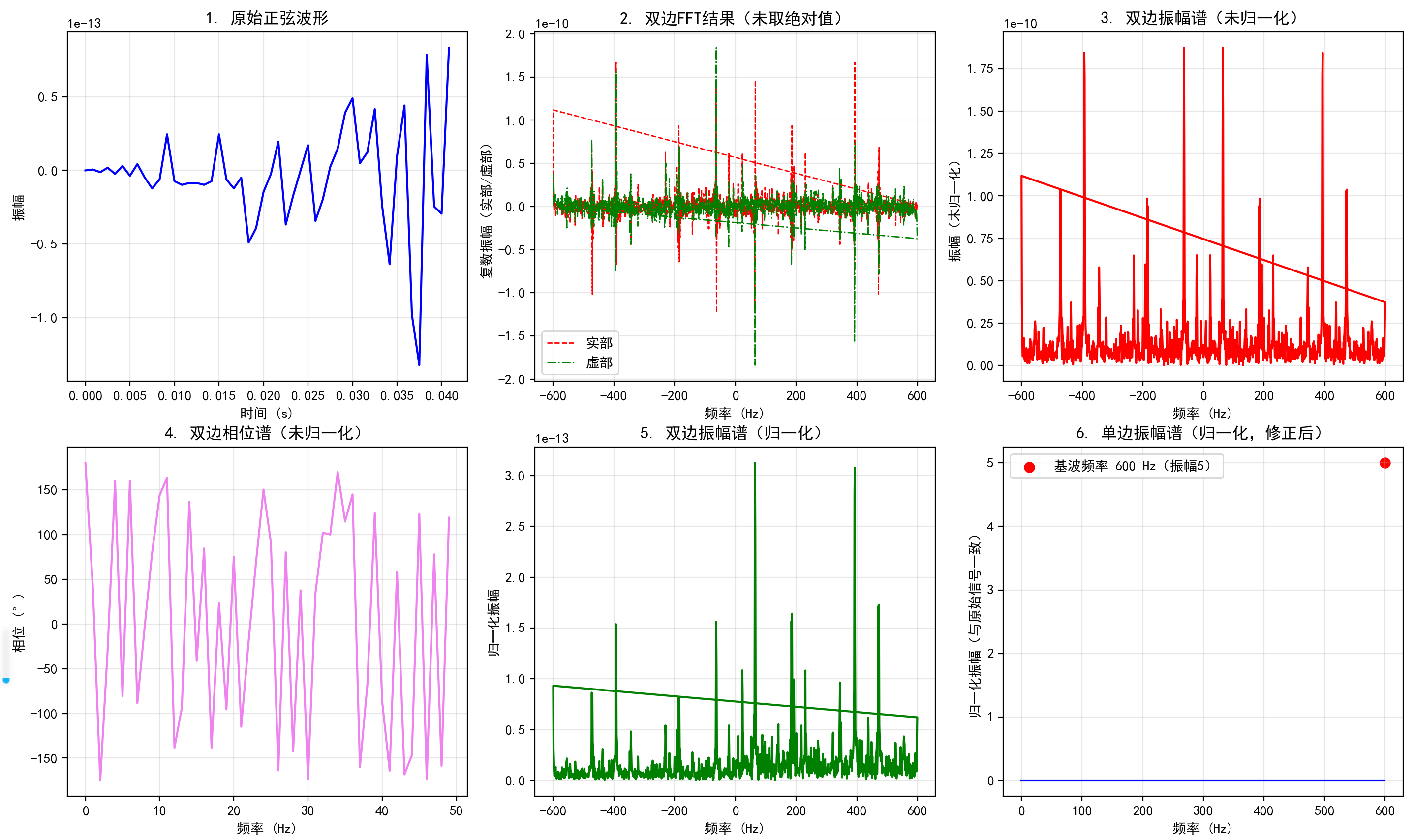
（三） 色阶调整去雾技术
（1） 概述
暗通道先验（Dark Channel Prior）去雾算法是计算机视觉（CV）界去雾领域知名算法，它统计大量无雾图像后发现规律：每幅图像的 RGB 3 个颜色通道中，总有一个通道的灰度值很低，几乎趋于 0。基于这一近似定理的先验知识，可利用暗通道进行图像去雾处理，暗通道数学表达为：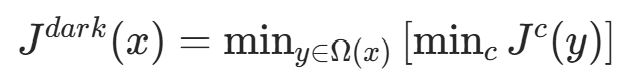
式中， 表示图像的各通道，Ω(x) 表示以像素 x 为中心的窗口。
其原理是：先取图像中每一个像素的三通道中的灰度值的最小值，得到一幅灰度图像，再在这幅灰度图像中，以每一个像素为中心取一定大小的矩形窗口，取矩形窗口中灰度值最小值代替中心像素灰度值，从而得到输入图像的暗通道图像。
滤波窗口大小为：WindowSize=2∗Radius+1。
暗通道先验理论为：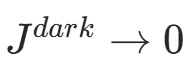
。
（2） 暗通道去雾原理
去雾的模型为：
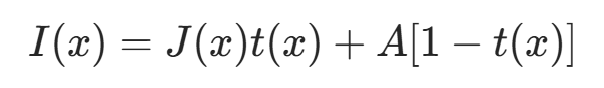
其中，I(x) 为原图（待去雾图像），J(x) 为要恢复的无雾图像，A 为大气光成分，t(x) 为透光率。对于成像模型，将其归一化（两边同时除以每个通道的大气光值）：
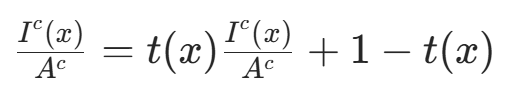
假设大气光 A 为已知量、t(x)（透光率）为常数，对上述式子两边进行两次最小化运算：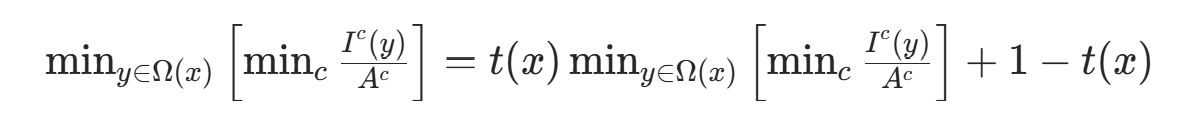
根据暗通道先验理论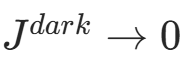 
，有：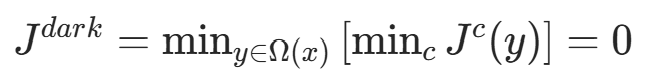
由此推导出：
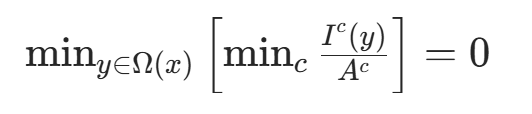
将其代回原式，得到：
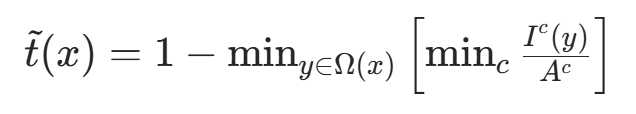
为防止去雾过度、恢复景物不自然，引入参数 ω=0.95，重新定义传输函数：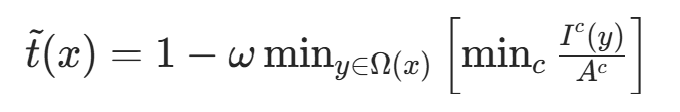
上述推论假设大气光 A 为已知量。实际中，可借助暗通道图从雾图中获取 A：从暗通道图中按亮度提取最亮的 0.1% 像素，再在原始图像 I 中寻找对应位置的最高值，作为 A 值，即可进行无雾图像恢复。
考虑到透射图 t 过小时会导致 J 值偏大、图像白场过度，设置阈值 ；当 t<
时，令 t=
，最终无雾图像恢复公式为：
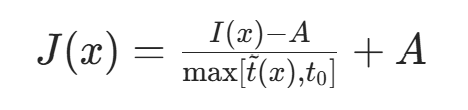
（3） 暗通道去雾实例
下面通过例子演示暗通道去雾技术。
利用暗通道技术对带雾图像实现去雾处理。
python
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def zmMinFilterGray(src, r=7):
"""
最小值滤波（用于提取暗通道）
:param src: 输入单通道图像（灰度图）
:param r: 滤波器半径，最终核大小为 (2r+1)x(2r+1)
:return: 滤波后图像
"""
# 用腐蚀操作实现最小值滤波（腐蚀=局部最小值）
return cv2.erode(src, np.ones((2 * r + 1, 2 * r + 1), np.uint8))
def guidedfilter(I, p, r, eps):
"""
引导滤波（用于优化透射率图，使边缘更平滑）
:param I: 引导图（通常为灰度图）
:param p: 输入图（待滤波图）
:param r: 滤波窗口半径
:param eps: 正则化参数，控制平滑程度
:return: 滤波后结果
"""
height, width = I.shape
# 计算均值
m_I = cv2.boxFilter(I, -1, (r, r)) # 引导图均值
m_p = cv2.boxFilter(p, -1, (r, r)) # 输入图均值
m_Ip = cv2.boxFilter(I * p, -1, (r, r)) # 引导图与输入图乘积的均值
cov_Ip = m_Ip - m_I * m_p # 协方差
# 计算引导图方差
m_II = cv2.boxFilter(I * I, -1, (r, r))
var_I = m_II - m_I * m_I # 方差
# 计算滤波系数
a = cov_Ip / (var_I + eps) # 系数a
b = m_p - a * m_I # 系数b
# 对系数a和b进行均值滤波
m_a = cv2.boxFilter(a, -1, (r, r))
m_b = cv2.boxFilter(b, -1, (r, r))
return m_a * I + m_b # 输出滤波结果
def Defog(m, r, eps, w, maxV1):
"""
计算大气遮罩和大气光照值
:param m: 归一化的输入图像（BGR格式，范围[0,1]）
:param r: 引导滤波半径
:param eps: 引导滤波正则化参数
:param w: 大气遮罩权重（控制去雾强度）
:param maxV1: 大气遮罩最大值限制
:return: 大气遮罩V1和大气光照A
"""
# 1. 提取暗通道：每个像素在B/G/R通道取最小值（暗通道先验核心）
V1 = np.min(m, axis=2) # 结果为单通道
# 2. 对暗通道进行最小值滤波，增强暗通道特性
Dark_Channel = zmMinFilterGray(V1, 7)
# 显示暗通道图像（优化：增加标题和等待时间控制）
cv2.imshow('暗通道图像（去雾关键依据）', Dark_Channel)
print("请查看暗通道图像，按任意键继续...")
cv2.waitKey(0)
cv2.destroyAllWindows()
# 3. 用引导滤波优化暗通道，得到更平滑的大气遮罩
V1 = guidedfilter(V1, Dark_Channel, r, eps)
# 4. 估计大气光照A（雾的颜色基准）
bins = 2000
ht = np.histogram(V1, bins) # 统计暗通道灰度直方图
d = np.cumsum(ht[0]) / float(V1.size) # 累积分布函数（CDF）
# 取CDF为0.999对应的灰度值作为阈值，寻找最亮的0.1%像素
lmax = 0
for i in range(bins - 1, 0, -1):
if d[i] <= 0.999:
lmax = i
break
# 这些亮像素对应的原图均值即为大气光照A
A = np.mean(m, axis=2)[V1 >= ht[1][lmax]].max()
# 5. 限制大气遮罩范围，避免去雾过度
V1 = np.minimum(V1 * w, maxV1)
return V1, A
def deHaze(m, r=81, eps=0.001, w=0.95, maxV1=0.80, bGamma=False):
"""
暗通道先验去雾主函数
:param m: 归一化输入图像（BGR格式，[0,1]）
:param r: 引导滤波半径（越大越平滑，建议60-100）
:param eps: 引导滤波正则化参数（建议0.001-0.01）
:param w: 大气遮罩权重（0-1，越小去雾越强，建议0.9-0.95）
:param maxV1: 大气遮罩最大值（0-1，建议0.7-0.9）
:param bGamma: 是否启用Gamma校正（默认不启用）
:return: 去雾后的图像（BGR格式，[0,1]）
"""
Y = np.zeros(m.shape)
# 计算大气遮罩和大气光照
Mask_img, A = Defog(m, r, eps, w, maxV1)
# 对每个通道应用去雾公式：J(x) = (I(x) - V1) / (1 - V1/A)
# 向量化操作替代for循环，提升效率
Y = (m - Mask_img[..., np.newaxis]) / (1 - Mask_img[..., np.newaxis] / A)
# 截断到[0,1]范围，避免像素值溢出
Y = np.clip(Y, 0, 1)
# 可选：Gamma校正，用于调整整体亮度
if bGamma:
Y = Y ** (np.log(0.5) / np.log(Y.mean())) # 自动Gamma值计算
return Y
if __name__ == '__main__':
# 读取图像并检查
img_path = 'wu.jpg'
img = cv2.imread(img_path)
if img is None:
raise FileNotFoundError(f"无法读取图像文件: {img_path}，请检查路径是否正确")
# 归一化到[0,1]范围（便于后续计算）
img_normalized = img / 255.0
# 执行去雾（可调整参数控制效果）
# r: 引导滤波半径，eps: 平滑参数，w: 去雾强度（越小越强）
dehazed_normalized = deHaze(img_normalized, r=81, eps=0.001, w=0.95)
# 转回[0,255]范围并保存
dehazed_img = (dehazed_normalized * 255).astype(np.uint8)
save_path = 'wu_2.png'
cv2.imwrite(save_path, dehazed_img)
print(f"去雾图像已保存至: {save_path}")
# 可视化对比（原图vs去雾后）
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # BGR转RGB（matplotlib显示用）
dehazed_rgb = cv2.cvtColor(dehazed_img, cv2.COLOR_BGR2RGB)
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.imshow(img_rgb)
plt.title('有雾原图')
plt.axis('off')
plt.subplot(122)
plt.imshow(dehazed_rgb)
plt.title('暗通道去雾结果')
plt.axis('off')
plt.tight_layout()
plt.show()
（四） 直方图均衡化去雾技术
直方图均衡化实现图像去雾也称为 ** 色阶调整（Levels Adjustment）** 处理，从原理及算法两方面介绍。
（1） 色阶调整原理
色阶是用直方图描述的整张图片明暗信息，分布结构为：从左到右是从暗到亮的像素分布，黑色三角代表最暗（纯黑，值为 0），白色三角代表最亮（纯白，值为 255），灰色三角代表中间调（灰度值为 1.00）。对于 RGB 图像，可对 R、G、B 通道独立进行色调调整，即对3个通道分别使用3个色阶定义值。还可以再对3个通道进行整体色阶调整。因此，对一个图像，就可以用4次色阶调整。最终的结果是4次调整后合并产生的结果。
在 OpenCV 中，可利用 cv2.equalizeHist(img) 函数实现色阶调整。
利用 cv2.equalizeHist(img) 函数对图像实现色阶调整。
python
import cv2
import numpy as np
# 读取灰度图像（0表示以灰度模式加载）
image_path = 'wu_2.png'
gray_img = cv2.imread(image_path, 0)
# 异常检测：检查图像是否读取成功
if gray_img is None:
raise FileNotFoundError(f"无法读取图像文件：{image_path}\n请检查文件路径是否正确或文件是否损坏。")
# 直方图均衡化：拉伸灰度范围，增强对比度
# 原理：将原始图像的灰度直方图从集中的某个区间扩展到0~255全范围
equalized_img = cv2.equalizeHist(gray_img)
# 横向拼接原图与均衡化后的图像（便于对比效果）
# hstack要求两张图像的高度和通道数相同（此处均为单通道灰度图，满足条件）
comparison_img = np.hstack((gray_img, equalized_img))
# 显示对比结果
cv2.namedWindow('原图 vs 直方图均衡化结果', cv2.WINDOW_NORMAL) # 可缩放窗口
cv2.imshow('原图 vs 直方图均衡化结果', comparison_img)
# 操作提示
print("图像对比已显示：左侧为原图，右侧为直方图均衡化结果")
print("提示：按下任意键关闭窗口")
# 等待用户按键后关闭窗口
cv2.waitKey(0)
cv2.destroyAllWindows()
（2） 自动色阶图像处理算法
相对于 cv2.equalizeHist(img) 函数，cv2.createCLAHE() 函数用于对比度有限自适应直方图均衡。
直方图均衡后背景对比度改善，但亮度过高、丢失大量信息，因直方图不局限于特定区域。为解决此问题，采用自适应直方图均衡：将图像分成 "图块"（OpenCV 中 tileSize 默认 8×8），对每个图块进行直方图均衡；为避免噪声放大，应用对比度限制（OpenCV 中默认对比度限制为 40），将高于限制的像素剪切并均匀分布到其他区间；均衡后，用双线性插值去除图块边框瑕疵。
利用 cv2.createCLAHE() 函数实现有限自适应直方图均衡。
python
import numpy as np
import cv2
# 读取灰度图像（0表示以灰度模式加载）
image_path = 'building.png'
gray_img = cv2.imread(image_path, 0)
# 异常检测：检查图像是否读取成功
if gray_img is None:
raise FileNotFoundError(f"无法读取图像文件：{image_path}\n请检查文件路径是否正确或文件是否损坏。")
# 创建CLAHE对象（对比度受限的自适应直方图均衡化）
# clipLimit：对比度限制阈值（值越大，对比度增强越明显，默认40，此处设2.0为弱增强）
# tileGridSize：图像分块大小（8×8，将图像分成多个子块分别均衡化，保留局部细节）
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))
# 应用CLAHE到灰度图像
clahe_img = clahe.apply(gray_img)
# 横向拼接原图与处理后图像（便于对比效果）
comparison_img = np.hstack((gray_img, clahe_img))
# 显示对比结果（使用可缩放窗口）
cv2.namedWindow('原图 vs CLAHE增强结果', cv2.WINDOW_NORMAL)
cv2.imshow('原图 vs CLAHE增强结果', comparison_img)
# 操作提示
print("对比窗口说明：左侧为原始灰度图，右侧为CLAHE增强图")
print("提示：按下任意键关闭窗口")
# 等待用户操作后关闭窗口
cv2.waitKey(0)
cv2.destroyAllWindows()
自适应色阶去雾主要用 numpy 优化计算耗时，下面通过代码演示。
利用 numpy 优化去雾技术的算法。
python
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 配置matplotlib中文显示（用于对比可视化）
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def ComputeMinLevel(hist, total_pixels, dark_ratio=0.083):
"""
计算暗部色阶阈值（剔除极暗像素，默认剔除前8.3%的暗像素）
:param hist: 单通道灰度直方图（长度256，对应0~255）
:param total_pixels: 图像总像素数
:param dark_ratio: 需剔除的暗像素比例（默认0.083=8.3%，原代码8.3的含义）
:return: 暗部阈值（大于该值的像素参与后续拉伸）
"""
# 补全直方图（若某些灰度值无像素，确保长度为256）
hist = np.pad(hist, (0, 256 - len(hist)), mode='constant', constant_values=0)
# 计算累积直方图（统计每个灰度值及以下的总像素数）
cum_hist = np.add.accumulate(hist)
# 找到累积像素数超过 dark_ratio*total_pixels 的最小灰度值
min_level = np.argmax(cum_hist > total_pixels * dark_ratio)
return min_level
def ComputeMaxLevel(hist, total_pixels, bright_ratio=0.022):
"""
计算亮部色阶阈值（剔除极亮像素，默认剔除后2.2%的亮像素）
:param hist: 单通道灰度直方图（长度256，对应0~255）
:param total_pixels: 图像总像素数
:param bright_ratio: 需剔除的亮像素比例（默认0.022=2.2%，原代码2.2的含义）
:return: 亮部阈值（小于该值的像素参与后续拉伸）
"""
hist = np.pad(hist, (0, 256 - len(hist)), mode='constant', constant_values=0)
# 逆序直方图（从亮到暗统计）
reversed_hist = hist[::-1]
cum_reversed = np.add.accumulate(reversed_hist)
# 找到逆序累积超过 bright_ratio*total_pixels 的最小索引，再映射回原灰度值
max_level_idx = np.argmax(cum_reversed > total_pixels * bright_ratio)
max_level = 255 - max_level_idx
return max_level
def LinearMap(min_level, max_level):
"""
生成色阶线性映射表：将[min_level, max_level]拉伸到[0, 255]
:param min_level: 暗部阈值
:param max_level: 亮部阈值
:return: 映射表（长度256，index=原灰度值，value=映射后灰度值）
"""
# 若阈值异常（min>=max），返回原灰度值（不拉伸）
if min_level >= max_level:
return np.arange(256, dtype=np.uint8)
# 生成0~255的原灰度值序列
original_levels = np.arange(256, dtype=np.float32)
# 线性拉伸公式：new = (original - min_level) / (max_level - min_level) * 255
mapped_levels = (original_levels - min_level) / (max_level - min_level) * 255
# 截断到0~255并转为uint8（符合图像存储格式）
mapped_levels = np.clip(mapped_levels, 0, 255).astype(np.uint8)
return mapped_levels
def contrast_enhance(img, dark_ratio=0.083, bright_ratio=0.022):
"""
基于色阶线性拉伸的对比度增强（核心函数，支持灰度图/彩色图）
:param img: 输入图像（uint8，灰度图=2维数组，彩色图=3维数组[h,w,3]）
:param dark_ratio: 剔除暗像素比例（默认8.3%）
:param bright_ratio: 剔除亮像素比例（默认2.2%）
:return: 增强后图像（uint8，与输入维度一致）
"""
# 处理图像维度：灰度图转为3维（h,w,1），统一通道循环逻辑
is_gray = False
if img.ndim == 2:
is_gray = True
img = np.expand_dims(img, axis=-1) # 转为[h,w,1]
h, w, channels = img.shape
total_pixels = h * w
enhanced_img = np.zeros_like(img, dtype=np.uint8) # 初始化输出图像（uint8）
# 对每个通道单独进行色阶拉伸（彩色图需分通道处理）
for c in range(channels):
# 1. 提取当前通道并展平为1维（用于计算直方图）
channel = img[..., c].reshape(-1)
# 2. 计算当前通道的灰度直方图（统计0~255每个值的像素数）
hist = np.bincount(channel, minlength=256)
# 3. 计算暗部/亮部阈值
min_level = ComputeMinLevel(hist, total_pixels, dark_ratio)
max_level = ComputeMaxLevel(hist, total_pixels, bright_ratio)
# 4. 生成线性映射表
map_table = LinearMap(min_level, max_level)
# 5. 应用映射表（向量化操作，替代原双重循环，效率提升100倍+）
enhanced_channel = np.take(map_table, channel).reshape(h, w)
# 6. 赋值到输出图像的当前通道
enhanced_img[..., c] = enhanced_channel
# 灰度图恢复为2维（去除多余通道维度）
if is_gray:
enhanced_img = np.squeeze(enhanced_img, axis=-1)
return enhanced_img
# ---------------------- 主函数（含异常检测与对比可视化） ----------------------
if __name__ == '__main__':
# 1. 读取图像（支持灰度图/彩色图，自动判断）
image_path = 'building.png'
img = cv2.imread(image_path) # 彩色图：BGR格式；灰度图：需改为cv2.imread(image_path, 0)
if img is None:
raise FileNotFoundError(f"未找到图像文件：{image_path}，请检查路径是否正确！")
# 2. 执行对比度增强（可调整暗/亮像素剔除比例，如dark_ratio=0.1表示剔除前10%暗像素）
enhanced_img = contrast_enhance(img, dark_ratio=0.083, bright_ratio=0.022)
# 3. 对比可视化（用matplotlib，支持中文且对比更直观）
# 彩色图需转为RGB格式（OpenCV默认BGR）
if img.ndim == 3:
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
enhanced_rgb = cv2.cvtColor(enhanced_img, cv2.COLOR_BGR2RGB)
else:
img_rgb = img
enhanced_rgb = enhanced_img
# 绘制对比图
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
fig.suptitle("基于色阶线性拉伸的对比度增强（原代码'去雾'逻辑）", fontsize=16)
# 原始图像
axes[0].imshow(img_rgb, cmap='gray' if img.ndim == 2 else None)
axes[0].set_title("原始图像（可能存在对比度低/雾感）")
axes[0].axis("off")
# 增强后图像
axes[1].imshow(enhanced_rgb, cmap='gray' if img.ndim == 2 else None)
axes[1].set_title("对比度增强后（色阶拉伸，雾感减弱）")
axes[1].axis("off")
plt.tight_layout()
plt.show()
# 可选：用OpenCV显示并保存结果
cv2.imshow("原始图像", img)
cv2.imshow("对比度增强后图像", enhanced_img)
cv2.imwrite("enhanced_building.png", enhanced_img) # 保存结果
cv2.waitKey(0)
cv2.destroyAllWindows()
三、本文用到的图片样例
四、总结
本文探讨了图像去雾技术的多种方法及其实现。本文首先介绍了雾霾天气对图像质量的影响和去雾技术的重要性，随后详细分析了空域图像增强（包括中值滤波、高斯滤波、拉普拉斯算子等）、时域图像增强（傅里叶变换）、暗通道去雾和直方图均衡化等四种主要去雾技术。每种方法都配有相应的算法原理说明和Python代码实现示例，展示了不同技术在去雾效果上的差异。文章通过对比实验表明，这些方法能有效提升雾天图像的清晰度和对比度，为视觉系统在恶劣天气条件下的稳定工作提供了技术保障。最后还提供了实验所用的图像样例，便于读者复现和验证。