【剑斩OFFER】优雅的解法——三数之和

一、题目描述

二、算法原理

⏩️1.排序

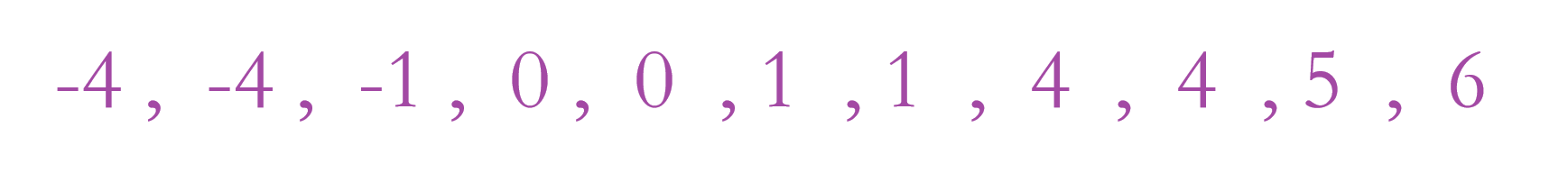
⏩️2、固定一个数 i ，在该数的后面利用双指针来快速找到满足条件的两个数。

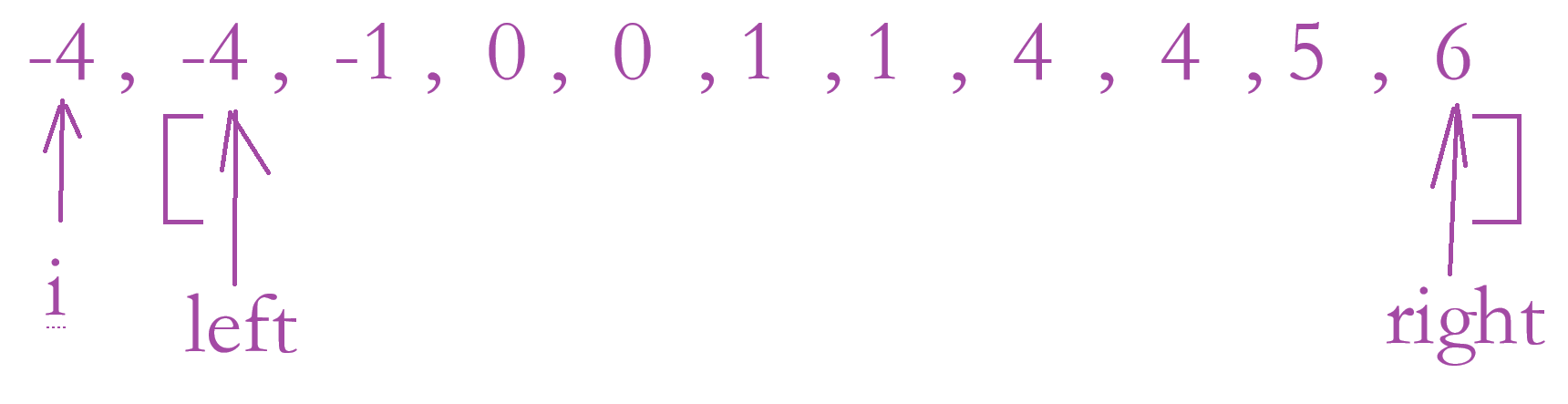
❌️提示：只要 i + left + right = 0，即满足条件，故 left + right = 4 即可。此时 left + right = 2 小于 4，所以 left++ ，继续找，如果 left + right > 4，则 right -- 。找到一种满足条件的两个数也不要停，遍历所有的结果。

⏩️ 3、去重

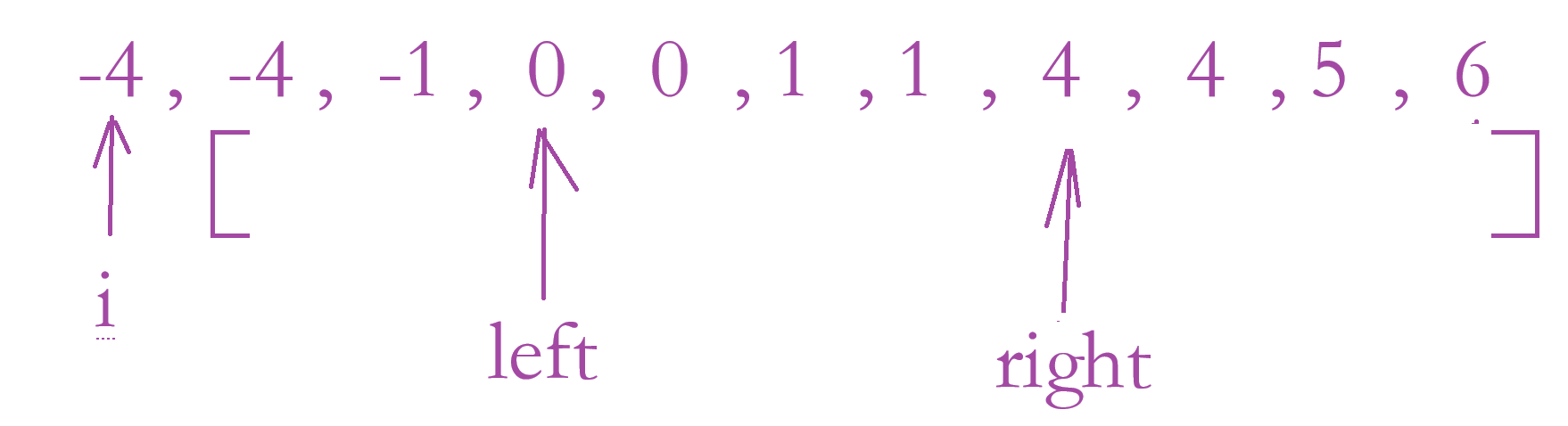
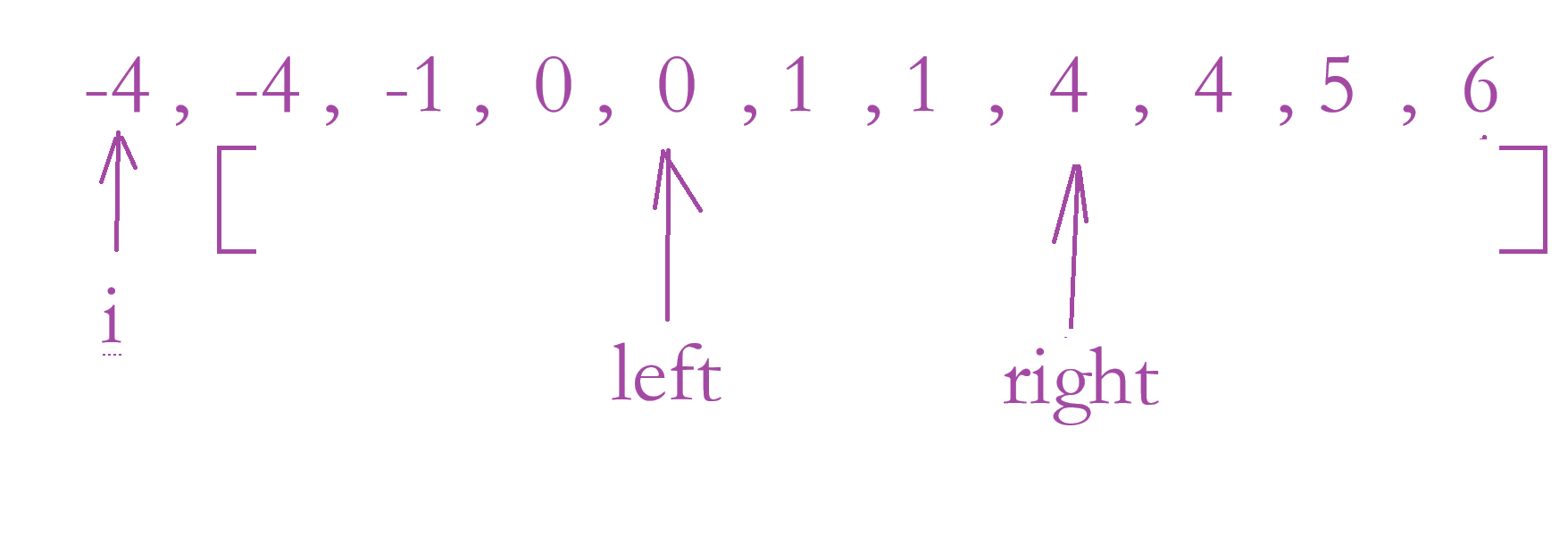
❌️注意：上面俩种情况都满足条件，我们只能取其中一个，所以 i 和 left 、right 在移动的过程中，下一个数和当前的数一样就跳过。left 和 right 在移动的过程中有可能会越界哦。还有一种情况：如果i >= 1，永远在后面找不到两俩个数加起来对于 - 1的，因为数组是有序的。

三、代码实现

cpp 复制代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> v;
        sort(nums.begin(),nums.end());
        int n = nums.size();
        for(int i = 0; i < n;)
        {
            if(nums[i] > 0)
            {
                break;
            }
            int left = i + 1;
            int right = nums.size() - 1;
            int target = -nums[i];
            while(left < right)
            {
                int sum = nums[left] + nums[right];
                if(sum > target)
                {
                    right--;
                }
                else if(sum < target)
                {
                    left++;
                }
                else{
                    v.push_back({nums[i],nums[left],nums[right]});
                    left++;
                    right--;

                    //去重
                    while(left < right && nums[left] == nums[left -1]) left++;
                    while(right > left && nums[right] == nums[right + 1]) right--;
                }
            }
            //去重
            i++;
            while(i < n && nums[i] == nums[i - 1]) i++;
        }
        return v;
    }

};

完！！