2024-CSP-J T3 小木棍

文章目录

题意

题目大意：给定n，求恰好使用n根火柴棍能够拼出最小的数

1.n根小木棍全部使用，若无法全部用上，则输出-1

2.拼出的数不能有前导0

思路

思路一时间少任务中，想骗分：

观察特殊性质，百分之60的数据是A、B性质，仔细读题得到结论，%7 = 0，全输出8，%7 =1 输出10+n/7-1个8
思路二数学推理找规律：

刚开始没思路可以直接在纸上求出前20根小棍能组成的数的情况
通过找规律可以发现：
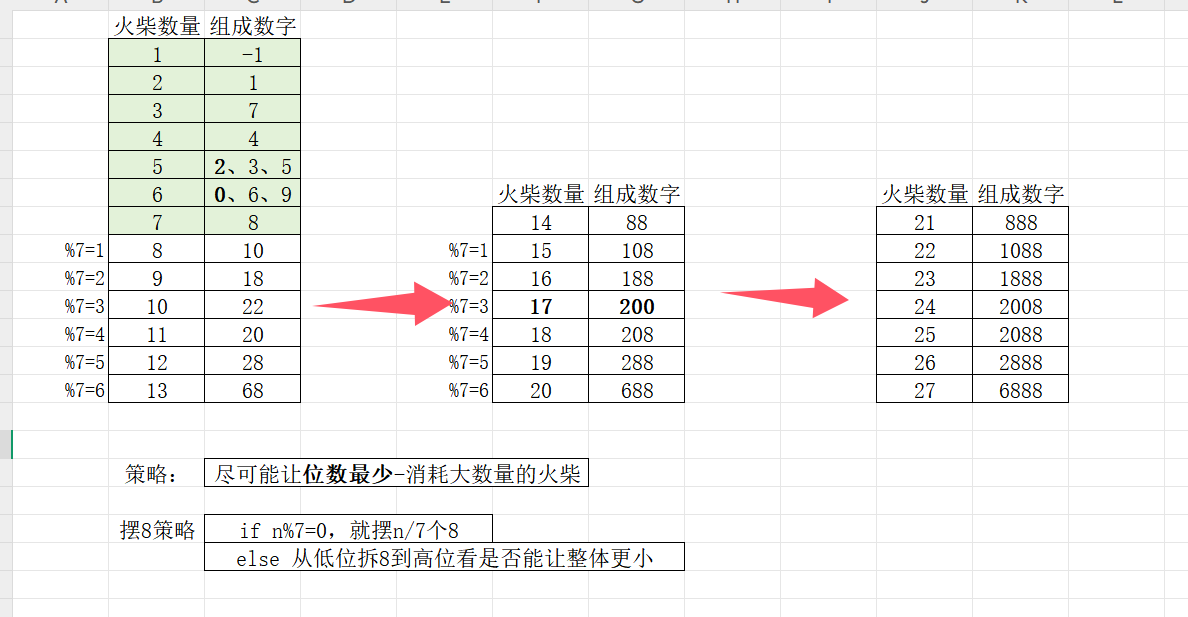
尽可能让数位最少（使用消耗木棍大的数字）、组成的数字最小(木棍量消耗相同则取较小的值)即可让值最小
①n%7= 0,就摆n/7个8(否则数位只会更多)
②n%7！= 0,高位拼凑组成较小的数字即可，低位大都取8
结论：
木棍>7 位数至少为两位，前面两位或者三位均能固定，后米的数字均为8
木棍<=7直接输出对应的数字

思路三背包DP：

由于木棍数n拼成的数与n-1、n-2、n-3、，，，n-7有关系（数位直接相关），即是由前面的数+k个木棍（k<=7）组成的最小值。因此考虑动态规划。

小木棍的总数量n作为背包容量，0~9每个数字作为物品种类，物品的体积是每个数字需要的小木棍数，对应的价值就是拼成的数字，每个物品可以重复使用，求价值最小--完全背包问题，

在求解时，如果dp设为组成的数值，由于组成的数和前几个没有必然联系，只能保证数位是直接相关的，所以设dp为当前i个木棍组成的最小数位，然后沿着dp路径取出具体的最少的数字即可

参考代码-60分

cpp 复制代码

//根据性质AB 60分版本 
//性质A，都为7的倍数，直接输出8
//性质B ，多了1，8根火柴拼成数字 1 0 
#include<bits/stdc++.h>
using namespace std;
int main()
{
//	freopen("sticks.in","r",stdin);
//	freopen(" sticks.out","w",stdout);	
	int t,n;
	cin>>t;
	
	while(t--){
		cin>>n;
		//性质A 
		if(n%7==0){
			for(int i=1;i<=n/7;i++)
				cout<<8;
			cout<<endl;
		}else if(n%7==1){ //性质B
			cout<<1<<0;
			for(int i=1;i<=(n-8)/7;i++)
				cout<<8; 
			cout<<endl;
		}
		
	} 
	
	return 0;
}

参考代码-找规律

cpp 复制代码

//根据性质  
//数字<=7直接输出对应的数字 
//数字>7 位数至少为两位，前面两位或者三位均能固定，后米的数字均为8 
#include<bits/stdc++.h>
using namespace std;
int a[8]={-1,-1,1,7,4,2,6,8} ;//表示I个木棍能组成的最小的数字 ，相同木棍数选数字较小的 
int main()
{
//	freopen("sticks.in","r",stdin);
//	freopen(" sticks.out","w",stdout);	
	int t,n,k=0;//k表示%7的结果 
	cin>>t;
	while(t--){
	    cin>>n;
	    k = n%7;
		if(n<=7) cout<<a[n]<<endl; 
		else if(k==0) {
			for(int i=1;i<=n/7;i++)
				cout<<8;
			cout<<endl;
		}else if(k==1){
			cout<<1<<0;
			for(int i=1;i<=(n-8)/7;i++)
				cout<<8;
			cout<<endl;
		}else if(k==2){
			cout<<1<<8;
			for(int i=1;i<=(n-9)/7;i++)
				cout<<8;
			cout<<endl;
		}else if(k==3){
			if(n==10)cout<<2<<2;
			else{
				cout<<2<<0<<0;//17个小棒需要特殊处理 
				for(int i=1;i<=(n-17)/7;i++)
					cout<<8;
				cout<<endl;
			}
			
		}else if(k==4){
			cout<<2<<0;
			for(int i=1;i<=(n-11)/7;i++)
				cout<<8;
			cout<<endl;
		}else if(k==5){
			cout<<2<<8;
			for(int i=1;i<=(n-12)/7;i++)
				cout<<8;
			cout<<endl;
		}else if(k==6){
			cout<<6<<8;
			for(int i=1;i<=(n-13)/7;i++)
				cout<<8;
			cout<<endl;
		}
	} 
	return 0;
}

参考代码-dp完全背包

cpp 复制代码

//dp求方案数
//数位最小即为最小 ,通过dp求出1e5以内的数据的最小数位 然后求出值即可 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int dp[N];
int a[]={6,2,5,5,4,5,6,3,7,6} ;//表示I个木棍能组成的最小的数字 ，相同木棍数选数字较小的 
void f_ans(int n);
int main(){
//	freopen("sticks.in","r",stdin);
//	freopen(" sticks.out","w",stdout);	
	int t,n,k=0;//k表示%7的结果  
	//dp求出值
	memset(dp,0x3f,sizeof(dp));//初始化为最大值 
	dp[0] = 0; //只需要初始化dp[0]，因为会用到，1根小棒不能拼成数，所以直接设为0x3f-很大的数值即可 
	for(int i=1;i<=1e5;i++){
		for(int j=0;j<=9;j++){ //七个数据可选 
			if(i>=a[j]){
				dp[i] = min(dp[i],dp[i-a[j]]+1);//找数位最小的情况 
			}
		}
	} 
	cin>>t;
	while(t--){
	    cin>>n;
	    f_ans(n);
	} 
	return 0;
}
void f_ans(int n){
	string ans;//存拼接的结果 
	bool flag = 1; 
	while(n){
		int num = -1;//默认无法组成一个正常的数 
		for(int i=0;i<=9;i++){ //挨个找 
			if(n>=a[i]&&dp[n] == dp[n-a[i]]+1) { //证会选a[i]个木棍组成较小的数
				//判断是否是第一个值 
				if(flag&&i==0) continue;
				else{
					flag = 0;
					num = i;
					break; //i从小到到，即组成的数值也是从小到大，所以即当前为木棍组成的数最小值 
				}
			}
		}
		if(num == -1){
			cout<<-1<<endl;
			return ;
		}
		ans += num + '0'; 
		n -= a[num];//剪掉耗费的木棍 
	}
	cout<<ans<<endl;

}