目录
[(一) 基本方法](#(一) 基本方法)
[(二) 后验概率最大化的含义](#(二) 后验概率最大化的含义)
[(一) 极大似然估计](#(一) 极大似然估计)
[(二) 学习与分类算法](#(二) 学习与分类算法)
[(三) 贝叶斯估计](#(三) 贝叶斯估计)
[(1)先验概率编辑 的极大似然估计](#(1)先验概率编辑 的极大似然估计)
[(2)条件概率 编辑的极大似然估计](#(2)条件概率 编辑的极大似然估计)
[(1)先验概率 编辑 的贝叶斯估计](#(1)先验概率 编辑 的贝叶斯估计)
[(2)条件概率 编辑 的贝叶斯估计](#(2)条件概率 编辑 的贝叶斯估计)
一、引言
朴素贝叶斯(naïve Bayes)法是基于贝叶斯定理与特征条件独立假设的分类方法(注意:朴素贝叶斯法与贝叶斯估计(Bayesian estimation)是不同的概念。)。对于给定的训练数据集,首先基于特征条件独立假设学习输入输出的联合概率分布;然后基于此模型,对给定的输入 x,利用贝叶斯定理求出后验概率最大的输出 y。朴素贝叶斯法实现简单,学习与预测的效率都很高,是一种常用的方法。本文叙述朴素贝叶斯法,包括朴素贝叶斯法的学习与分类、朴素贝叶斯法的参数估计算法,以及Python代码完整实现。
二、朴素贝叶斯法的学习与分类
(一) 基本方法
设输入空间 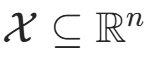 为 n 维向量的集合,输出空间为类标记集合
为 n 维向量的集合,输出空间为类标记集合 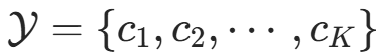 。输入为特征向量
。输入为特征向量 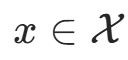 ,输出为类标记(class label)
,输出为类标记(class label)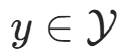 。X 是定义在输入空间
。X 是定义在输入空间 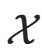 上的随机向量,Y 是定义在输出空间
上的随机向量,Y 是定义在输出空间 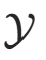 上的随机变量。P(X,Y) 是 X 和 Y 的联合概率分布。训练数据集
上的随机变量。P(X,Y) 是 X 和 Y 的联合概率分布。训练数据集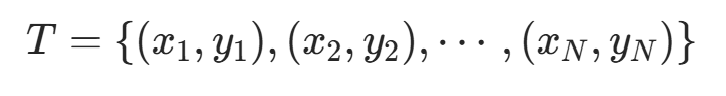 由 P(X,Y) 独立同分布产生。
由 P(X,Y) 独立同分布产生。
朴素贝叶斯法通过训练数据集学习联合概率分布 P(X,Y)。具体地,学习以下先验概率分布 及条件概率分布。
-
先验概率分布:
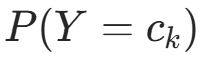 ,
, -
条件概率分布:
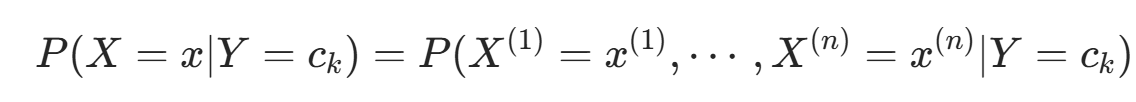 ,
,
于是学习到联合概率分布 P(X,Y)。
由于条件概率分布 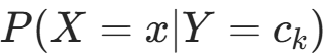 有指数级数量的参数,直接估计实际不可行。朴素贝叶斯法引入条件独立性假设 :
有指数级数量的参数,直接估计实际不可行。朴素贝叶斯法引入条件独立性假设 :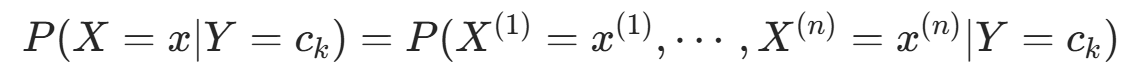
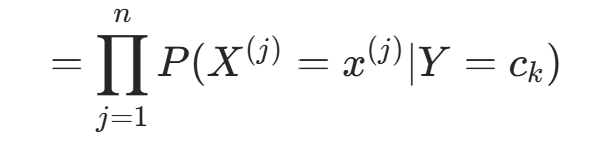
该假设使朴素贝叶斯法简化(属于生成模型),但可能牺牲部分分类准确率。
朴素贝叶斯法分类时,对输入 x,通过模型计算后验概率分布 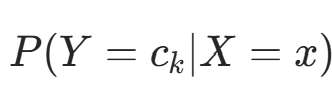 ,并输出后验概率最大的类。根据贝叶斯定理:
,并输出后验概率最大的类。根据贝叶斯定理:,得朴素贝叶斯分类的基本公式:
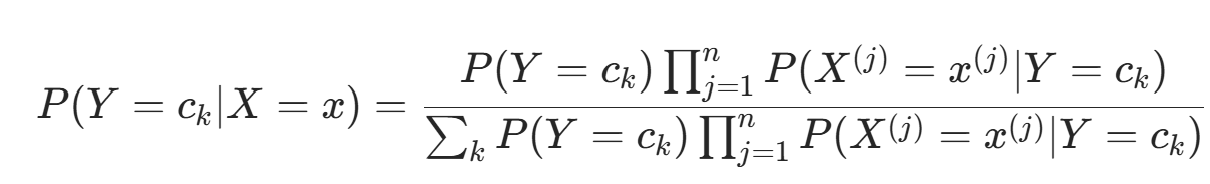 ,
,
因此,朴素贝叶斯分类器可表示为:y=f(x)=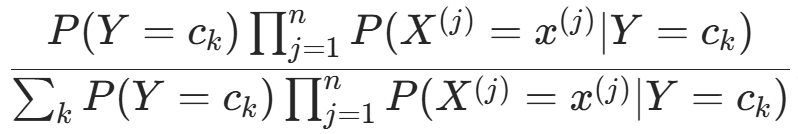
注意到式 中分母对所有 相同,因此可简化为:
(二) 后验概率最大化的含义
朴素贝叶斯法将实例分到后验概率最大的类中,这等价于期望风险最小化 。假设选择 0-1 损失函数:
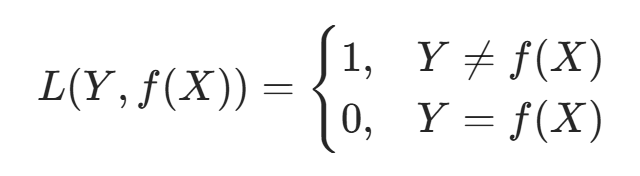 其中 f(X) 是分类决策函数。此时期望风险函数为:
其中 f(X) 是分类决策函数。此时期望风险函数为: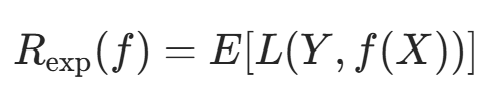
对联合分布 P(X,Y) 取条件期望,得: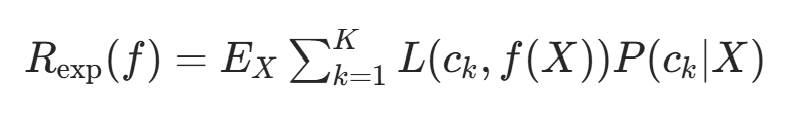
为最小化期望风险,对每个 X=x 极小化风险: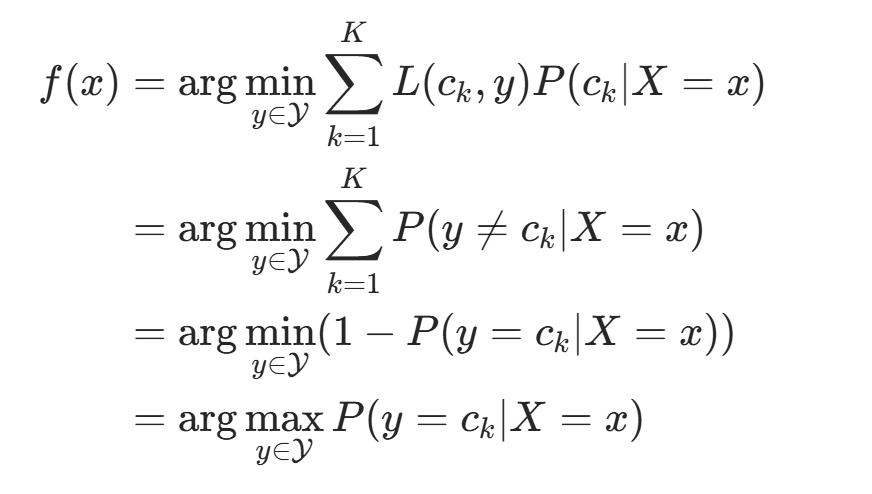
由此,期望风险最小化准则等价于后验概率最大化准则 :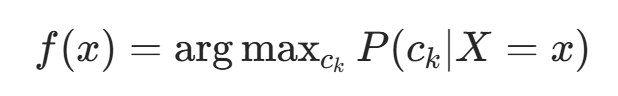
三、朴素贝叶斯法的参数估计
(一) 极大似然估计
朴素贝叶斯法中,学习需估计 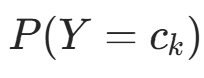 和
和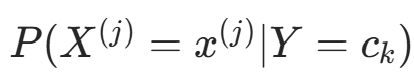 ,可通过极大似然估计实现。
,可通过极大似然估计实现。
-
先验概率
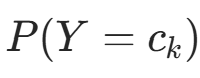 的极大似然估计:
的极大似然估计: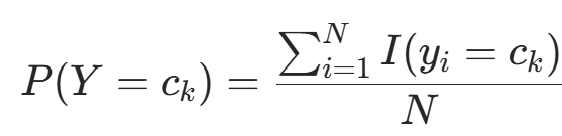 ,k=1,2,⋯,K(I(⋅) 为指示函数,满足条件时取 1,否则取 0)
,k=1,2,⋯,K(I(⋅) 为指示函数,满足条件时取 1,否则取 0) -
条件概率
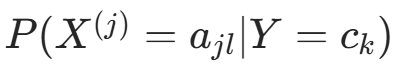 的极大似然估计:设第 j 个特征
的极大似然估计:设第 j 个特征 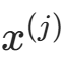 的取值集合为
的取值集合为 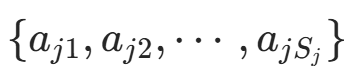 ,则:
,则: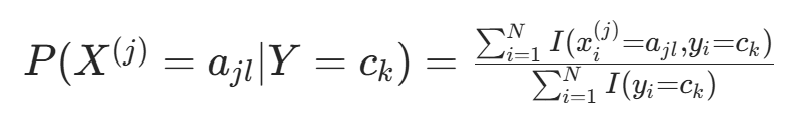 ;k=1,2,⋯,K
;k=1,2,⋯,K
(二) 学习与分类算法
算法 1(朴素贝叶斯算法)
- 输入 :训练数据
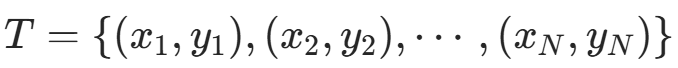 (其中
(其中 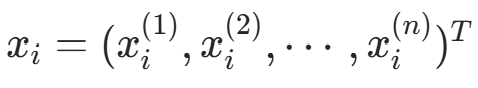 ,
,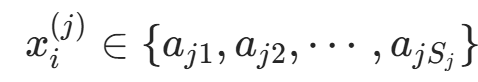 ,
,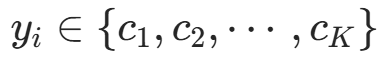 );实例 x。
);实例 x。 - 输出:实例 x 的分类。
-
计算先验概率 及条件概率 :
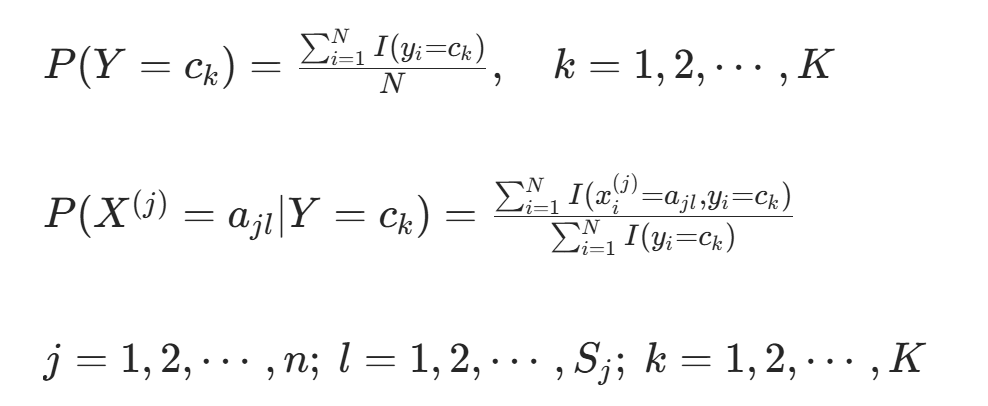
-
对给定实例
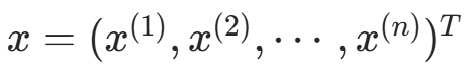 ,计算:
,计算: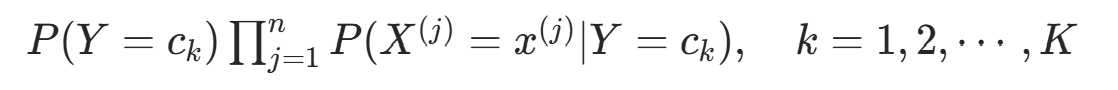
-
确定实例 x 的类:
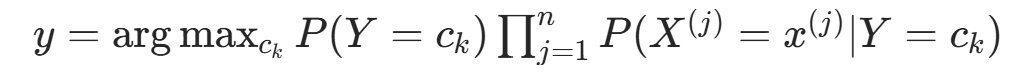
例 1 由表 1 的训练数据学习朴素贝叶斯分类器,确定 的类标记 y。表中
为特征,取值集合
={1,2,3},
={S,M,L};类标记 Y∈{1,−1}。
表 1 训练数据
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | |
| S | M | M | S | S | S | M | M | L | L | L | M | M | L | L | |
| Y | -1 | -1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 | -1 |
解 根据算法 1,计算概率:
- 先验概率:
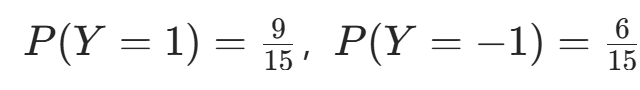 。
。 - 条件概率 Y=1 时:
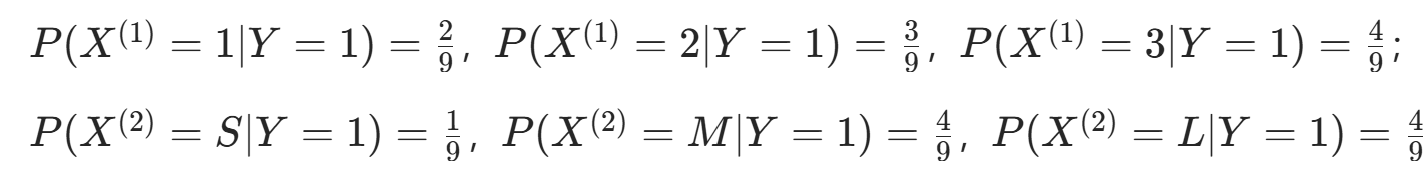 。
。 - 条件概率Y=−1 时:
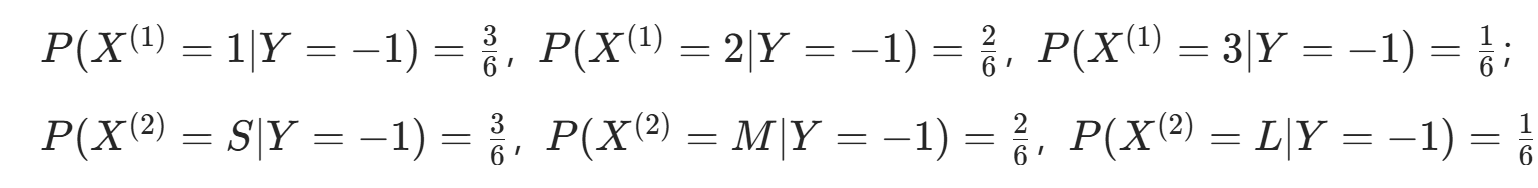 。
。
对 计算:
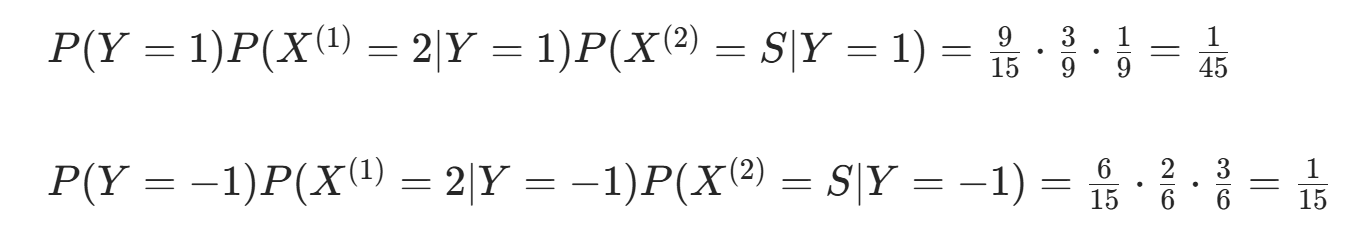
因 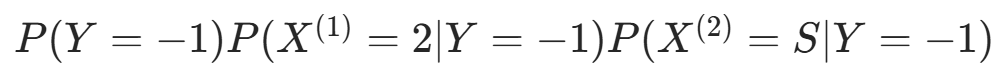 更大,故 y=−1。
更大,故 y=−1。
(三) 贝叶斯估计
极大似然估计可能出现概率为 0 的情况,导致后验概率计算偏差。贝叶斯估计可解决此问题,核心是对频数加 "伪计数" λ。
-
条件概率的贝叶斯估计:
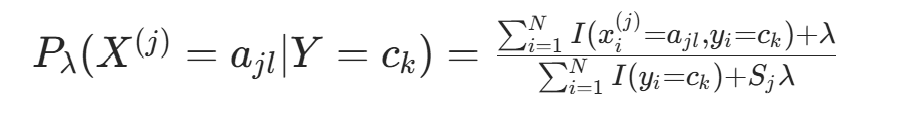 (λ≥0,λ=0 时退化为极大似然估计;λ=1 为拉普拉斯平滑)
(λ≥0,λ=0 时退化为极大似然估计;λ=1 为拉普拉斯平滑) -
先验概率的贝叶斯估计:
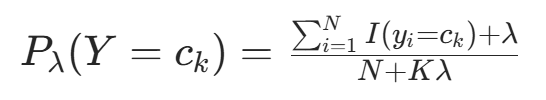
例 2 同例 1,取拉普拉斯平滑 λ=1。
解 ={1,2,3},
={S,M,L},C={1,−1}。计算得:
- 先验概率:
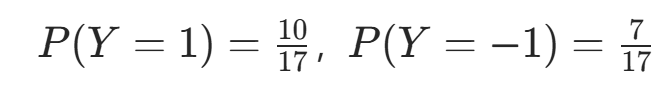 。
。 - 条件概率Y=1 时:
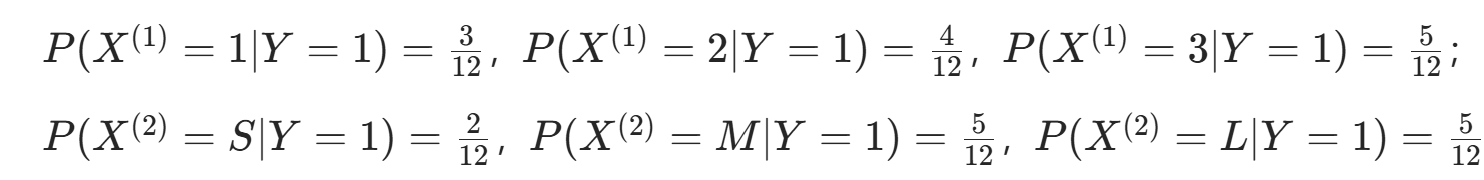 。
。 - 条件概率Y=−1 时:
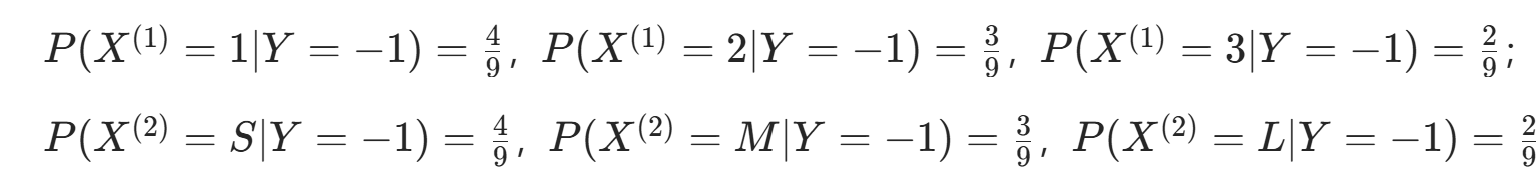 。
。
对 计算:
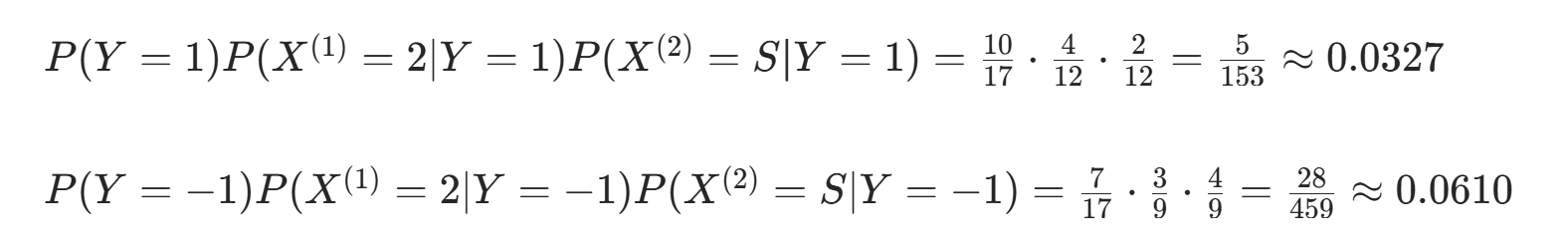
因 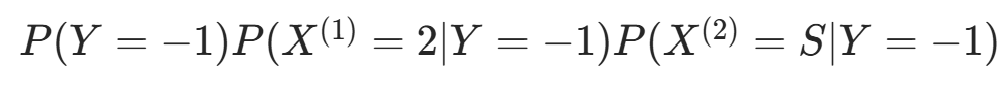 更大,故 y=−1。
更大,故 y=−1。
四、习题
1.用极大似然估计法推出朴素贝叶斯法中的概率估计的两个公式。
(1)先验概率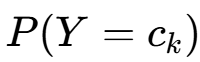 的极大似然估计
的极大似然估计
极大似然估计的核心是 "找到使观测数据联合概率最大的参数"。
-
似然函数构造 :训练集
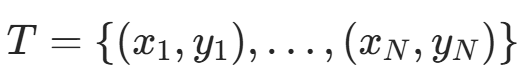 独立同分布,联合概率(似然函数)为:
独立同分布,联合概率(似然函数)为: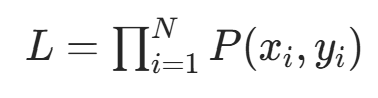 ,由朴素贝叶斯的联合概率分解
,由朴素贝叶斯的联合概率分解 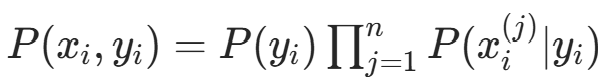 ,似然函数可拆分为:
,似然函数可拆分为: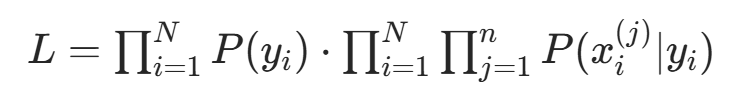
-
先验概率的似然部分 :仅关注
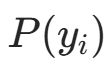 的部分,记
的部分,记 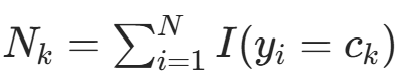 (类别
(类别 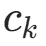 的样本数),则似然为:
的样本数),则似然为: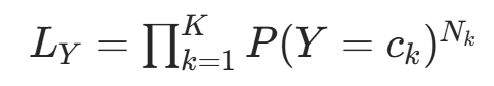
-
对数似然与拉格朗日乘数法 :取对数似然:
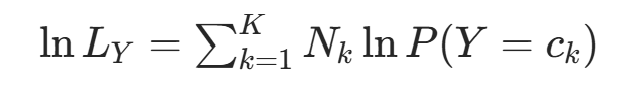 约束条件为
约束条件为 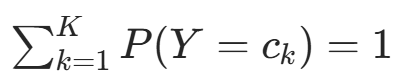 。构造拉格朗日函数:
。构造拉格朗日函数: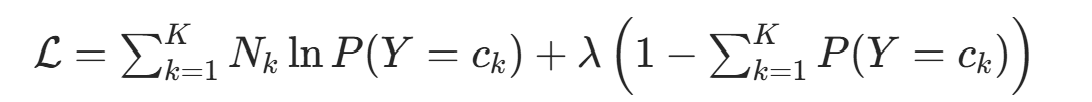 对
对 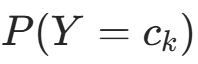 求偏导并令其为 0:
求偏导并令其为 0: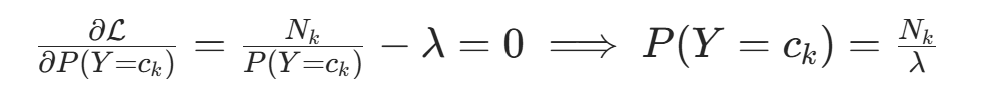 代入约束
代入约束 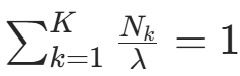 ,得
,得 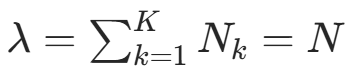 (总样本数)。因此可得公式:
(总样本数)。因此可得公式: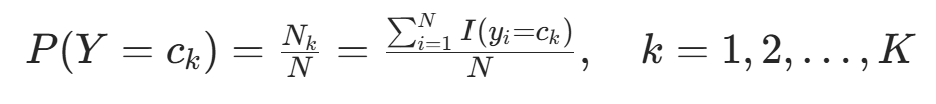
(2)条件概率 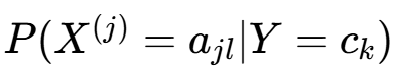 的极大似然估计
的极大似然估计
对每个特征 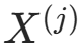 和类别
和类别 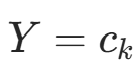 ,记
,记 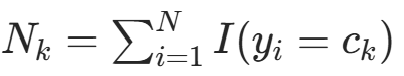 (类别
(类别 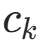 的样本数),
的样本数),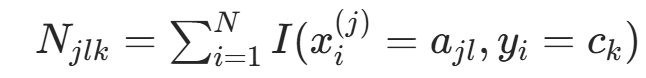 (类别
(类别 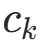 中特征
中特征 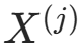 取
取 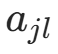 的样本数)。
的样本数)。
-
似然函数的条件部分 :在
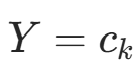 的子集中,特征
的子集中,特征 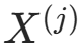 的似然为:
的似然为: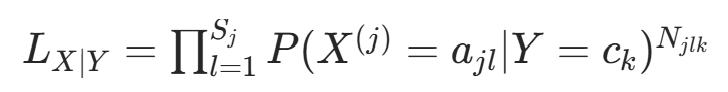 (
(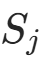 是
是 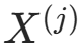 的取值个数)。
的取值个数)。 -
对数似然与拉格朗日乘数法 :取对数似然:
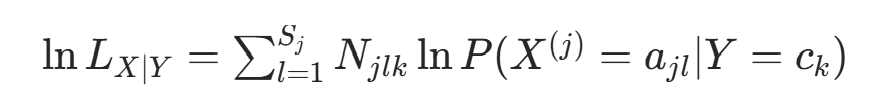 约束条件为
约束条件为 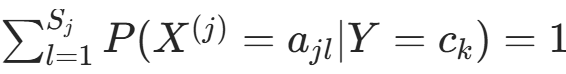 。构造拉格朗日函数:
。构造拉格朗日函数: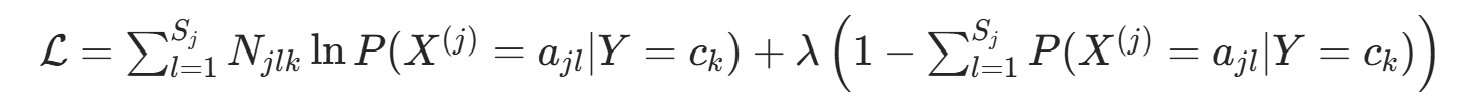 对
对 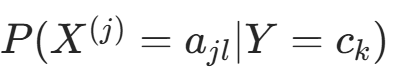 求偏导并令其为 0:
求偏导并令其为 0: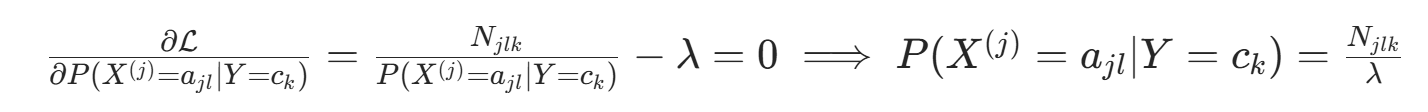 代入约束
代入约束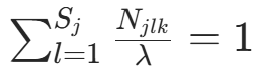 ,得
,得 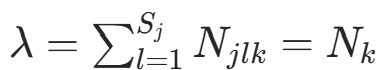 (类别
(类别 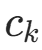 的样本数)。因此得到公式:
的样本数)。因此得到公式: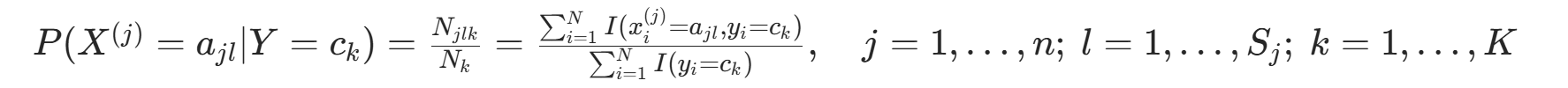 。
。
- 用贝叶斯估计法推出朴素贝叶斯法中的概率估计的两个公式。
贝叶斯估计的核心是 "将参数视为随机变量,用先验分布 + 观测数据推导后验分布,再以后验分布的期望 / 众数作为估计值"。拉普拉斯平滑是贝叶斯估计的特殊情况(采用对称 Dirichlet 先验)。
(1)先验概率 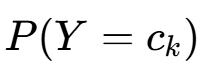 的贝叶斯估计
的贝叶斯估计
-
先验分布选择 :先验概率
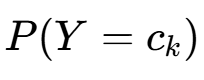 服从Dirichlet 分布
服从Dirichlet 分布 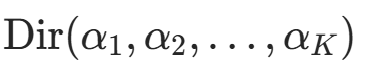 (Multinomial 分布的共轭先验)。拉普拉斯平滑中,取对称先验
(Multinomial 分布的共轭先验)。拉普拉斯平滑中,取对称先验  (λ>0,为 "伪计数")。
(λ>0,为 "伪计数")。 -
后验分布推导 :根据贝叶斯定理,后验分布
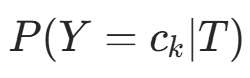 仍为 Dirichlet 分布,参数更新为
仍为 Dirichlet 分布,参数更新为 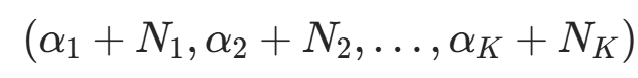 ,其中
,其中 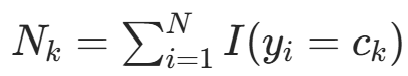 (观测到的类别计数)。
(观测到的类别计数)。 -
后验期望作为估计值 :Dirichlet 分布
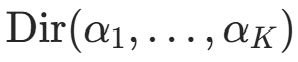 的期望为
的期望为 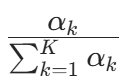 。因此,先验概率的贝叶斯估计为后验分布的期望:
。因此,先验概率的贝叶斯估计为后验分布的期望: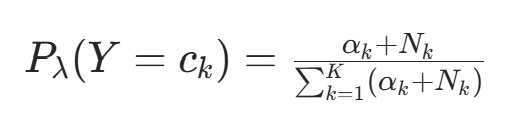 代入对称先验
代入对称先验 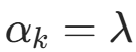 ,得:
,得: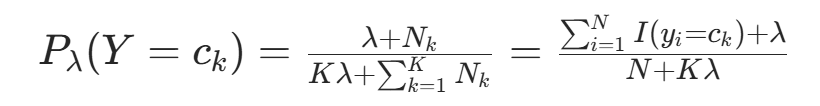 (因为
(因为 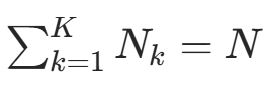 ,总样本数),当 λ=1 时,就是拉普拉斯平滑。
,总样本数),当 λ=1 时,就是拉普拉斯平滑。
(2)条件概率 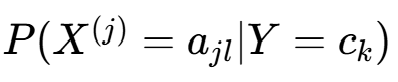 的贝叶斯估计
的贝叶斯估计
-
先验分布选择 :在
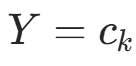 的条件下,特征
的条件下,特征 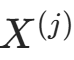 的取值
的取值  服从 Multinomial 分布,其共轭先验为 Dirichlet 分布
服从 Multinomial 分布,其共轭先验为 Dirichlet 分布 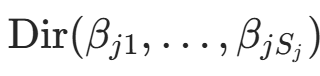 。拉普拉斯平滑中,取对称先验
。拉普拉斯平滑中,取对称先验 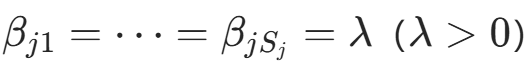 。
。 -
后验分布推导 :在
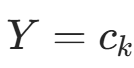 的子集中(样本数
的子集中(样本数 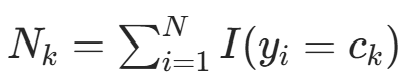 ),记
),记 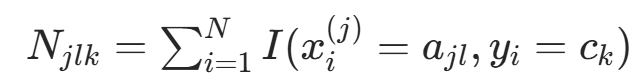 (特征
(特征 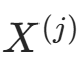 取
取 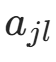 的计数)。后验分布
的计数)。后验分布 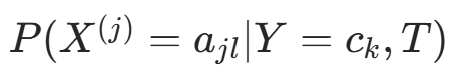 为 Dirichlet 分布,参数更新为
为 Dirichlet 分布,参数更新为 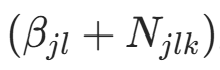 。
。 -
后验期望作为估计值 :Dirichlet 分布
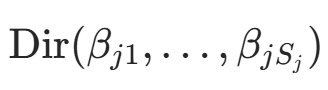 的期望为
的期望为 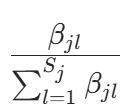 。因此,条件概率的贝叶斯估计为后验分布的期望:
。因此,条件概率的贝叶斯估计为后验分布的期望: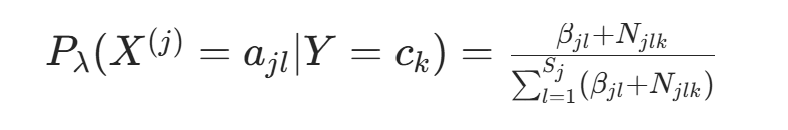 代入对称先验
代入对称先验 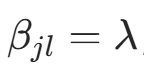 ,得:
,得: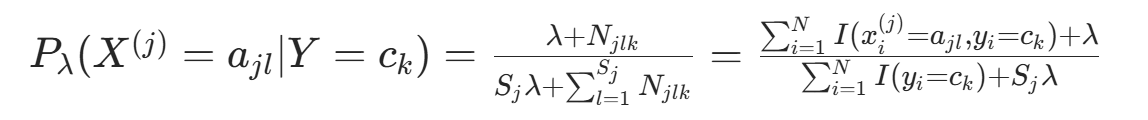 (因为
(因为 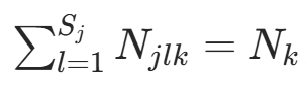 ,类别
,类别  的样本数),。当 λ=1 时,确保了 "即使某类特征取值未出现(
的样本数),。当 λ=1 时,确保了 "即使某类特征取值未出现(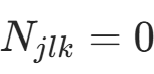 ),概率也不为 0",避免后验计算中出现 "0 概率传递" 的问题。
),概率也不为 0",避免后验计算中出现 "0 概率传递" 的问题。
五、Python代码完整实现
python
# 导入依赖库
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
# 朴素贝叶斯类实现
class NaiveBayes:
def __init__(self, laplace_lambda=0):
"""
初始化朴素贝叶斯分类器
laplace_lambda: 拉普拉斯平滑系数,0表示极大似然估计,>0表示贝叶斯估计(平滑)
"""
self.laplace_lambda = laplace_lambda # 拉普拉斯平滑参数
self.prior_probs = {} # 存储先验概率 P(Y=ck)
self.cond_probs = {} # 存储条件概率 P(Xj=ajl | Y=ck)
self.classes = None # 类别集合
self.feature_values = {} # 每个特征的可能取值(用于平滑和预测)
def fit(self, X, y):
"""训练朴素贝叶斯模型,学习先验概率和条件概率"""
n_samples, n_features = X.shape
self.classes = np.unique(y) # 获取所有类别
# 记录每个特征的唯一取值(用于后续概率计算)
for feature_idx in range(n_features):
self.feature_values[feature_idx] = np.unique(X[:, feature_idx])
# --- 1. 计算先验概率 P(Y=ck) ---
for class_label in self.classes:
class_count = np.sum(y == class_label) # 类别class_label的样本数
if self.laplace_lambda > 0:
# 贝叶斯估计(拉普拉斯平滑)
self.prior_probs[class_label] = (class_count + self.laplace_lambda) / (
n_samples + len(self.classes) * self.laplace_lambda
)
else:
# 极大似然估计
self.prior_probs[class_label] = class_count / n_samples
# --- 2. 计算条件概率 P(Xj=ajl | Y=ck) ---
for class_label in self.classes:
X_class = X[y == class_label] # 类别为class_label的子数据集
n_samples_class = X_class.shape[0] # 子数据集的样本数
for feature_idx in range(n_features):
feature_unique_vals = self.feature_values[feature_idx] # 该特征的所有可能取值
for val in feature_unique_vals:
# 统计子数据集中,该特征取val的样本数
val_count = np.sum(X_class[:, feature_idx] == val)
if self.laplace_lambda > 0:
# 贝叶斯估计(拉普拉斯平滑)
self.cond_probs[(feature_idx, val, class_label)] = (val_count + self.laplace_lambda) / (
n_samples_class + len(feature_unique_vals) * self.laplace_lambda
)
else:
# 极大似然估计(注意:若n_samples_class=0,概率为0)
self.cond_probs[
(feature_idx, val, class_label)] = val_count / n_samples_class if n_samples_class > 0 else 0
def predict(self, X):
"""对输入样本进行分类预测"""
predictions = []
for sample in X:
class_scores = {} # 存储每个类别的"后验概率分数"
for class_label in self.classes:
score = self.prior_probs[class_label] # 先验概率初始化分数
for feature_idx in range(len(sample)):
val = sample[feature_idx]
# 乘以该特征取值的条件概率(若不存在,分数置0)
score *= self.cond_probs.get((feature_idx, val, class_label), 0)
class_scores[class_label] = score
# 选择分数最高的类别作为预测结果
predictions.append(max(class_scores, key=class_scores.get))
return np.array(predictions)
# 示例数据与模型训练
# 特征X:第一列是X(1),第二列是X(2)(S→0, M→1, L→2)
X = np.array([
[1, 0], [1, 1], [1, 1], [1, 0], [1, 0],
[2, 0], [2, 1], [2, 1], [2, 2], [2, 2],
[3, 2], [3, 1], [3, 1], [3, 2], [3, 2]
])
# 标签y:类别{-1, 1}
y = np.array([-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1])
# 测试样本:x=(2, S)^T → 编码为[2, 0]
X_test = np.array([[2, 0]])
# 模型训练与预测
# 1. 极大似然估计(Laplace λ=0)
nb_mle = NaiveBayes(laplace_lambda=0)
nb_mle.fit(X, y)
y_pred_mle = nb_mle.predict(X_test)
print("极大似然估计预测结果:", y_pred_mle)
# 2. 贝叶斯估计(拉普拉斯平滑,λ=1)
nb_bayes = NaiveBayes(laplace_lambda=1)
nb_bayes.fit(X, y)
y_pred_bayes = nb_bayes.predict(X_test)
print("贝叶斯估计(拉普拉斯平滑)预测结果:", y_pred_bayes)
# 打印概率计算过程
def print_mle_probs(nb):
"""打印极大似然估计的概率计算过程"""
print("\n=== 极大似然估计(Laplace λ=0)的概率计算 ===")
# 1. 先验概率 P(Y=c_k)
print("1. 先验概率:")
for c in sorted(nb.classes):
prob = nb.prior_probs[c]
print(f" P(Y={c}) = {prob:.4f} (精确值:{prob.numerator}/{prob.denominator})"
if hasattr(prob, 'numerator') else f" P(Y={c}) = {prob:.4f}")
# 2. 条件概率 P(X^{(j)}=v | Y=c_k)
# 特征X(1)的条件概率
print("\n2. 特征X(1)的条件概率 P(X(1)=v | Y=c):")
for c in sorted(nb.classes):
for v in nb.feature_values[0]:
prob = nb.cond_probs.get((0, v, c), 0)
print(f" P(X(1)={v} | Y={c}) = {prob:.4f} (精确值:{prob.numerator}/{prob.denominator})"
if hasattr(prob, 'numerator') else f" P(X(1)={v} | Y={c}) = {prob:.4f}")
# 特征X(2)的条件概率
print("\n3. 特征X(2)的条件概率 P(X(2)=v | Y=c):")
for c in sorted(nb.classes):
for v in nb.feature_values[1]:
prob = nb.cond_probs.get((1, v, c), 0)
print(f" P(X(2)={v} | Y={c}) = {prob:.4f} (精确值:{prob.numerator}/{prob.denominator})"
if hasattr(prob, 'numerator') else f" P(X(2)={v} | Y={c}) = {prob:.4f}")
# 3. 测试样本后验分数计算
x1, x2 = 2, 0 # 测试样本(2, S)的编码
score_1 = nb.prior_probs[1] * nb.cond_probs.get((0, x1, 1), 0) * nb.cond_probs.get((1, x2, 1), 0)
score_neg1 = nb.prior_probs[-1] * nb.cond_probs.get((0, x1, -1), 0) * nb.cond_probs.get((1, x2, -1), 0)
print("\n4. 测试样本 x=(2, S)(编码为[2, 0])的后验分数:")
print(f" P(Y=1) * P(X(1)=2|Y=1) * P(X(2)=0|Y=1) = {score_1:.4f} (精确值:9/15 * 3/9 * 1/9 = {1 / 45:.4f})")
print(f" P(Y=-1) * P(X(1)=2|Y=-1) * P(X(2)=0|Y=-1) = {score_neg1:.4f} (精确值:6/15 * 2/6 * 3/6 = {1 / 15:.4f})")
print(f" 因为 {score_neg1:.4f} > {score_1:.4f},所以预测类别: {-1}")
def print_bayes_probs(nb):
"""打印贝叶斯估计(拉普拉斯平滑)的概率计算过程"""
print("\n=== 贝叶斯估计(拉普拉斯平滑 λ=1)的概率计算 ===")
# 1. 先验概率 P(Y=c_k)
print("1. 先验概率:")
for c in sorted(nb.classes):
prob = nb.prior_probs[c]
print(f" P(Y={c}) = {prob:.4f} (精确值:{prob.numerator}/{prob.denominator})"
if hasattr(prob, 'numerator') else f" P(Y={c}) = {prob:.4f}")
# 2. 条件概率 P(X^{(j)}=v | Y=c_k)
# 特征X(1)的条件概率
print("\n2. 特征X(1)的条件概率 P(X(1)=v | Y=c):")
for c in sorted(nb.classes):
for v in nb.feature_values[0]:
prob = nb.cond_probs.get((0, v, c), 0)
print(f" P(X(1)={v} | Y={c}) = {prob:.4f} (精确值:{prob.numerator}/{prob.denominator})"
if hasattr(prob, 'numerator') else f" P(X(1)={v} | Y={c}) = {prob:.4f}")
# 特征X(2)的条件概率
print("\n3. 特征X(2)的条件概率 P(X(2)=v | Y=c):")
for c in sorted(nb.classes):
for v in nb.feature_values[1]:
prob = nb.cond_probs.get((1, v, c), 0)
print(f" P(X(2)={v} | Y={c}) = {prob:.4f} (精确值:{prob.numerator}/{prob.denominator})"
if hasattr(prob, 'numerator') else f" P(X(2)={v} | Y={c}) = {prob:.4f}")
# 3. 测试样本后验分数计算
x1, x2 = 2, 0 # 测试样本(2, S)的编码
score_1 = nb.prior_probs[1] * nb.cond_probs.get((0, x1, 1), 0) * nb.cond_probs.get((1, x2, 1), 0)
score_neg1 = nb.prior_probs[-1] * nb.cond_probs.get((0, x1, -1), 0) * nb.cond_probs.get((1, x2, -1), 0)
print("\n4. 测试样本 x=(2, S)(编码为[2, 0])的后验分数:")
print(
f" P(Y=1) * P(X(1)=2|Y=1) * P(X(2)=0|Y=1) = {score_1:.4f} (精确值:10/17 * 4/12 * 2/12 = {5 / 153:.4f} ≈ 0.0327)")
print(
f" P(Y=-1) * P(X(1)=2|Y=-1) * P(X(2)=0|Y=-1) = {score_neg1:.4f} (精确值:7/17 * 3/9 * 4/9 = {28 / 459:.4f} ≈ 0.0610)")
print(f" 因为 {score_neg1:.4f} > {score_1:.4f},所以预测类别: {-1}")
# 调用打印函数
print_mle_probs(nb_mle)
print_bayes_probs(nb_bayes)
# 可视化功能实现
# 1. 先验概率柱状图
def plot_prior_probs(nb, title):
"""绘制先验概率柱状图"""
classes = list(nb.prior_probs.keys())
probs = [nb.prior_probs[c] for c in classes]
plt.bar(classes, probs, color=['skyblue', 'lightgreen'])
plt.title(title)
plt.xlabel("Class Label")
plt.ylabel("Prior Probability")
plt.ylim(0, 1)
plt.grid(axis='y', alpha=0.3)
plt.show()
# 绘制两种估计的先验概率
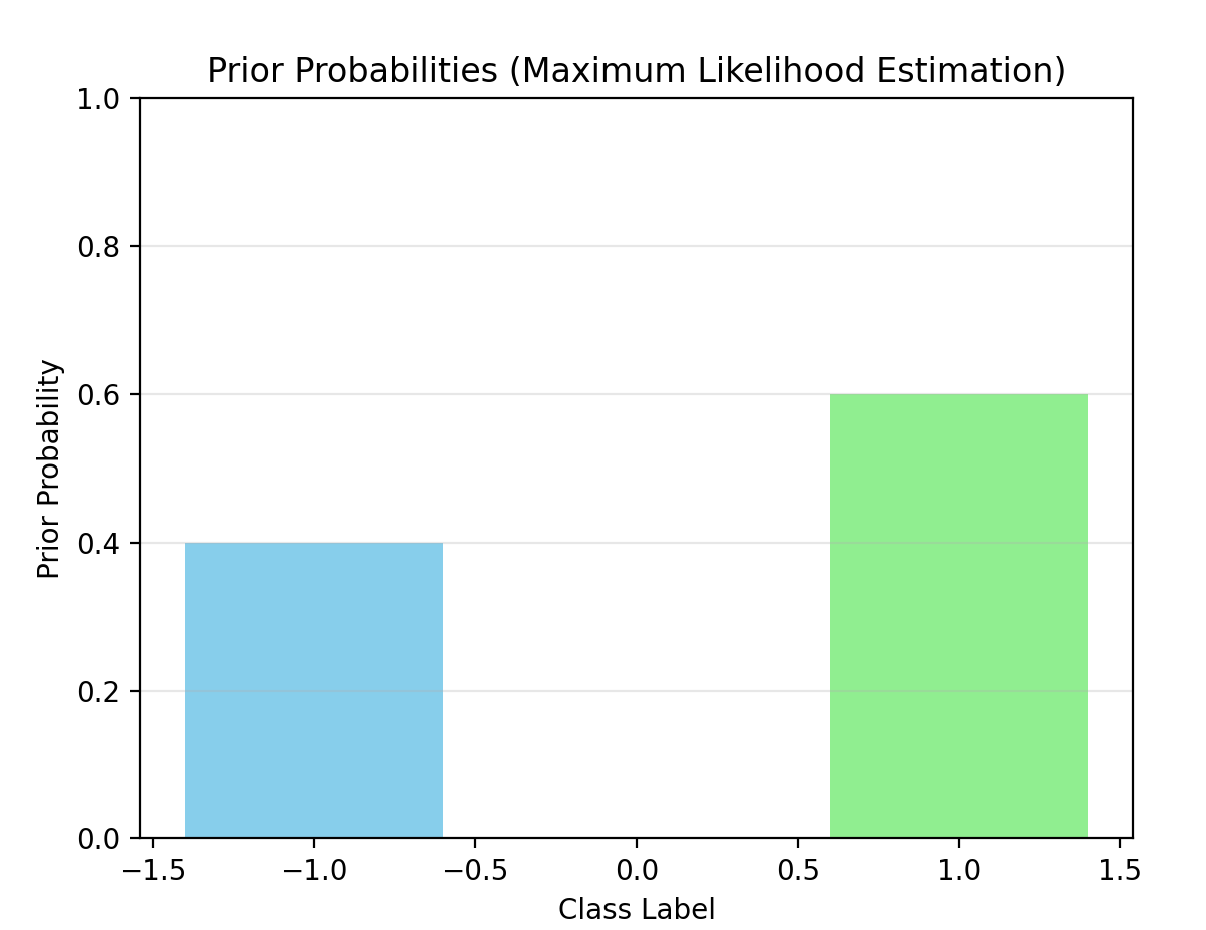
plot_prior_probs(nb_mle, "Prior Probabilities (Maximum Likelihood Estimation)")
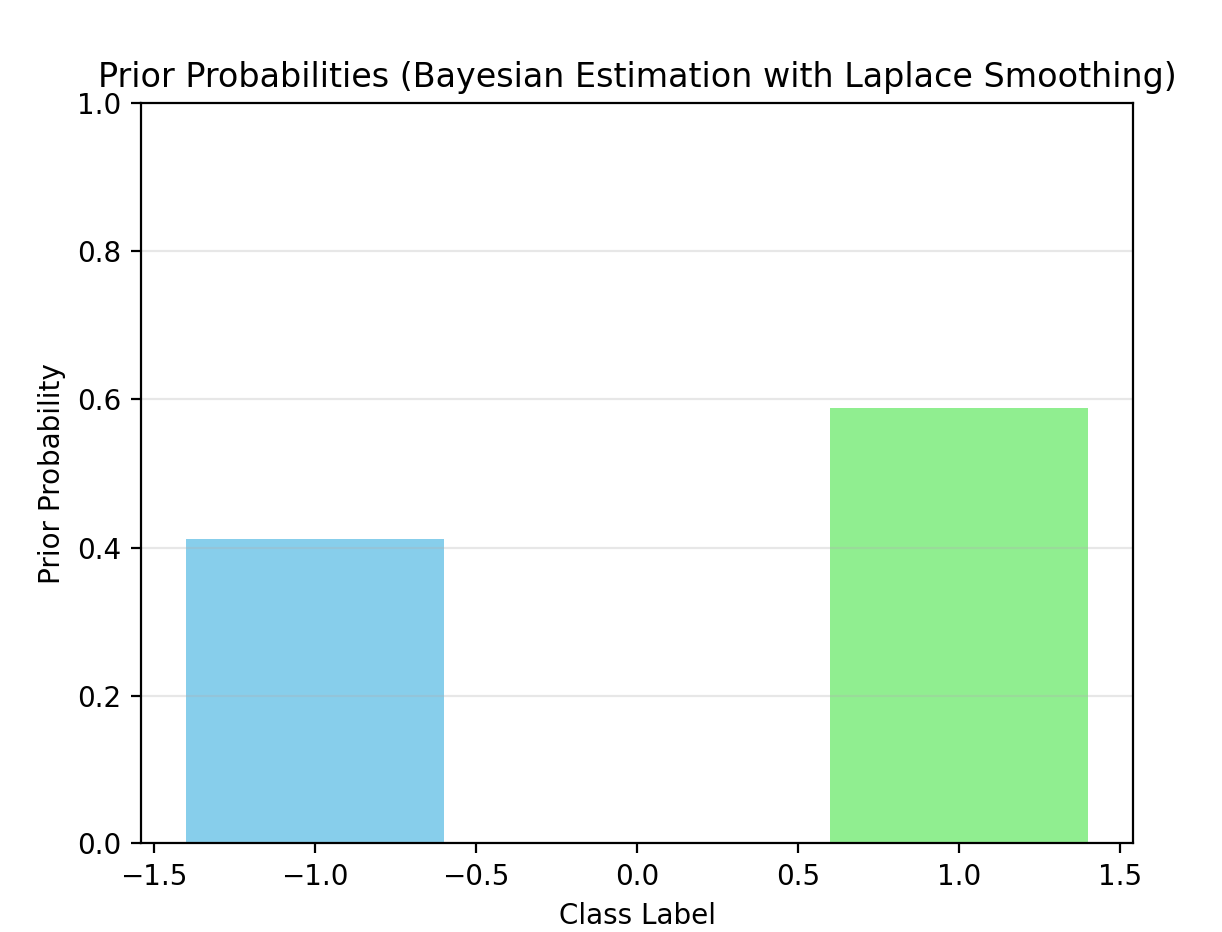
plot_prior_probs(nb_bayes, "Prior Probabilities (Bayesian Estimation with Laplace Smoothing)")
# 2. 条件概率热力图
def plot_cond_probs(nb, feature_idx, title):
"""绘制单个特征的条件概率热力图 P(X[feature_idx]=v | Y=c)"""
classes = list(nb.prior_probs.keys())
feature_vals = nb.feature_values[feature_idx]
# 构建条件概率矩阵(行=类别,列=特征值)
cond_prob_matrix = np.zeros((len(classes), len(feature_vals)))
for i, c in enumerate(classes):
for j, v in enumerate(feature_vals):
cond_prob_matrix[i, j] = nb.cond_probs.get((feature_idx, v, c), 0)
# 热力图可视化
sns.heatmap(
cond_prob_matrix, annot=True, fmt=".2f",
xticklabels=feature_vals, yticklabels=classes,
cmap="YlGnBu", cbar=False
)
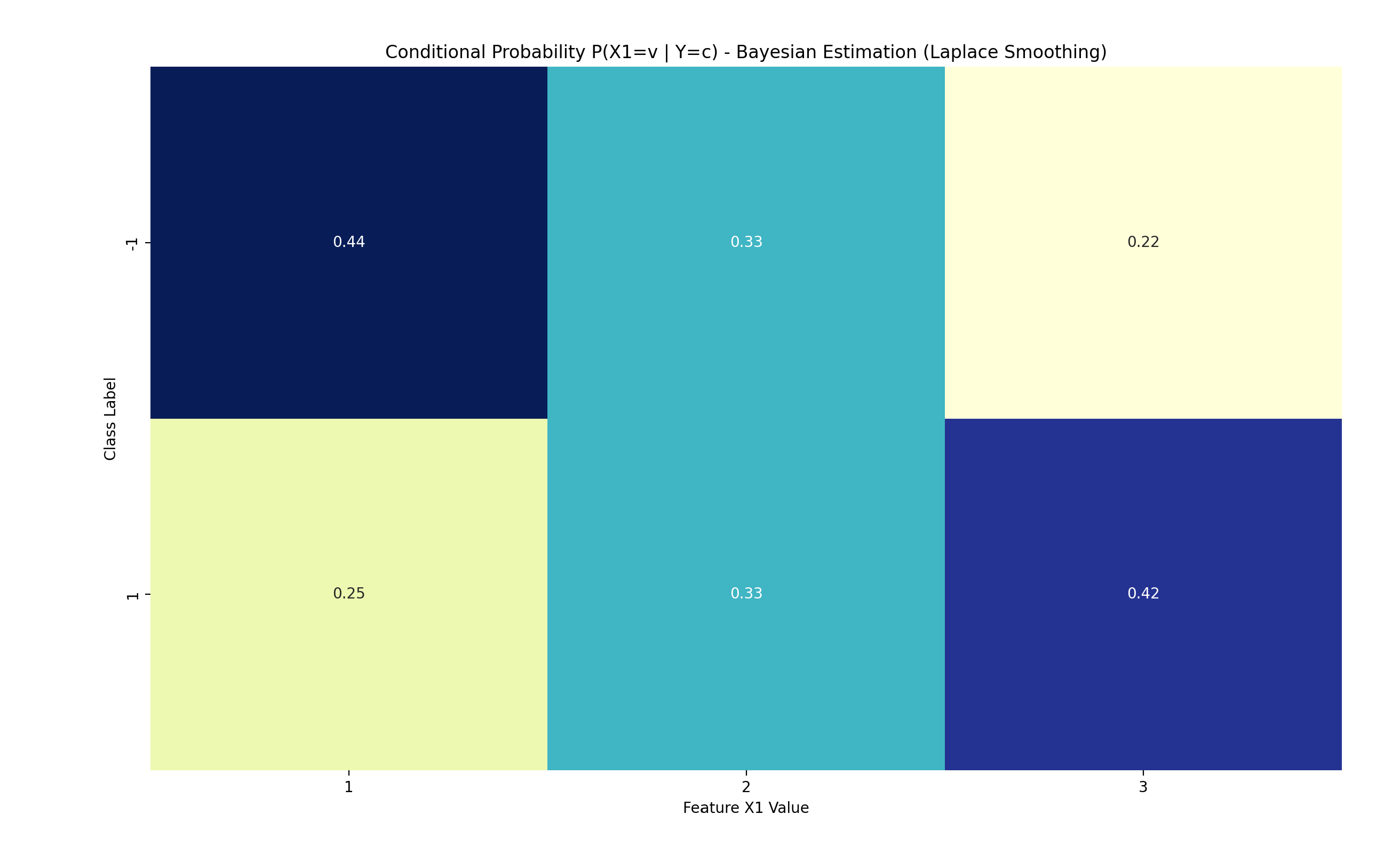
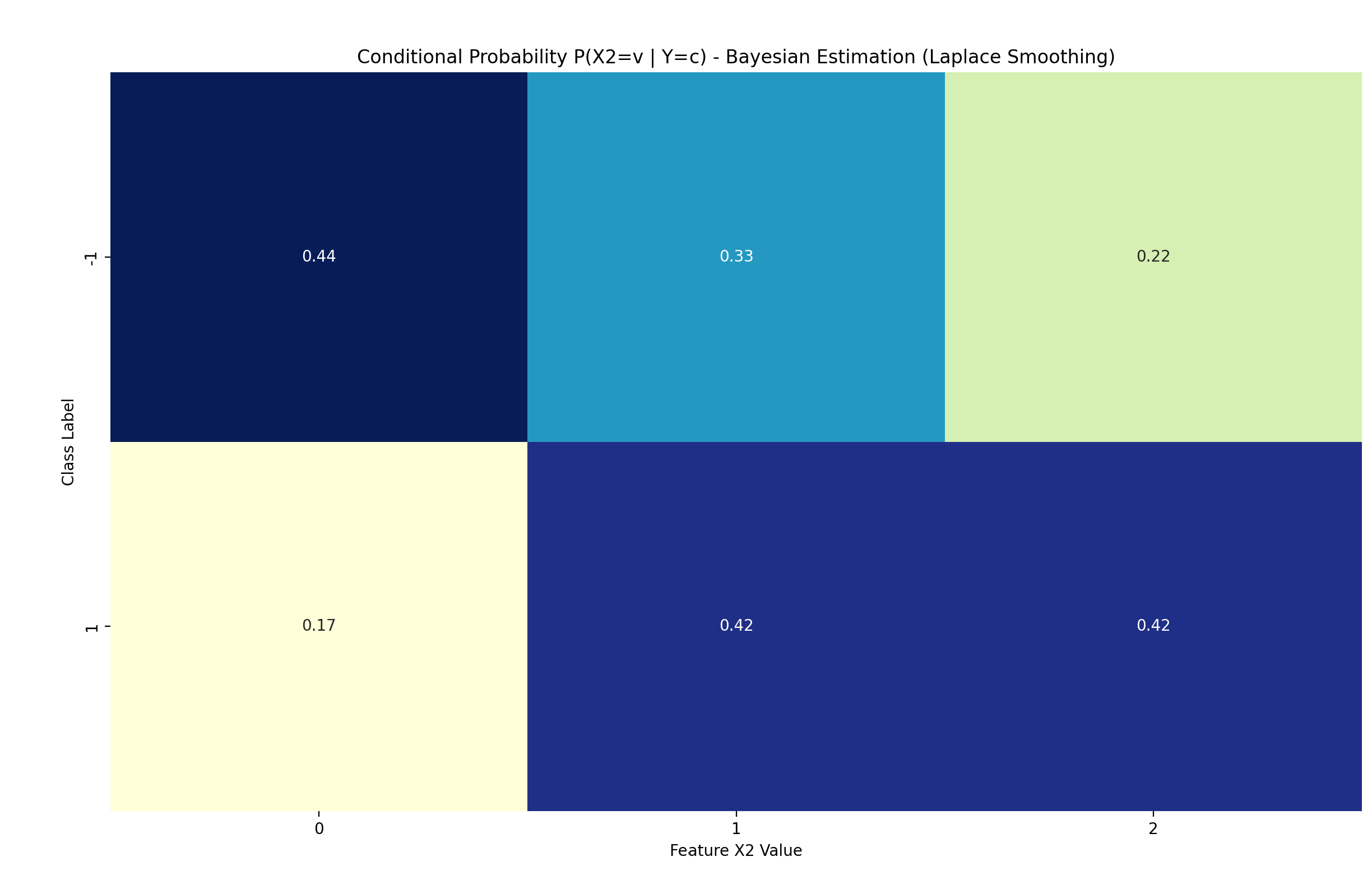
plt.title(f"Conditional Probability P(X{feature_idx + 1}=v | Y=c) - {title}")
plt.xlabel(f"Feature X{feature_idx + 1} Value")
plt.ylabel("Class Label")
plt.show()
# 绘制两个特征的条件概率(极大似然估计)
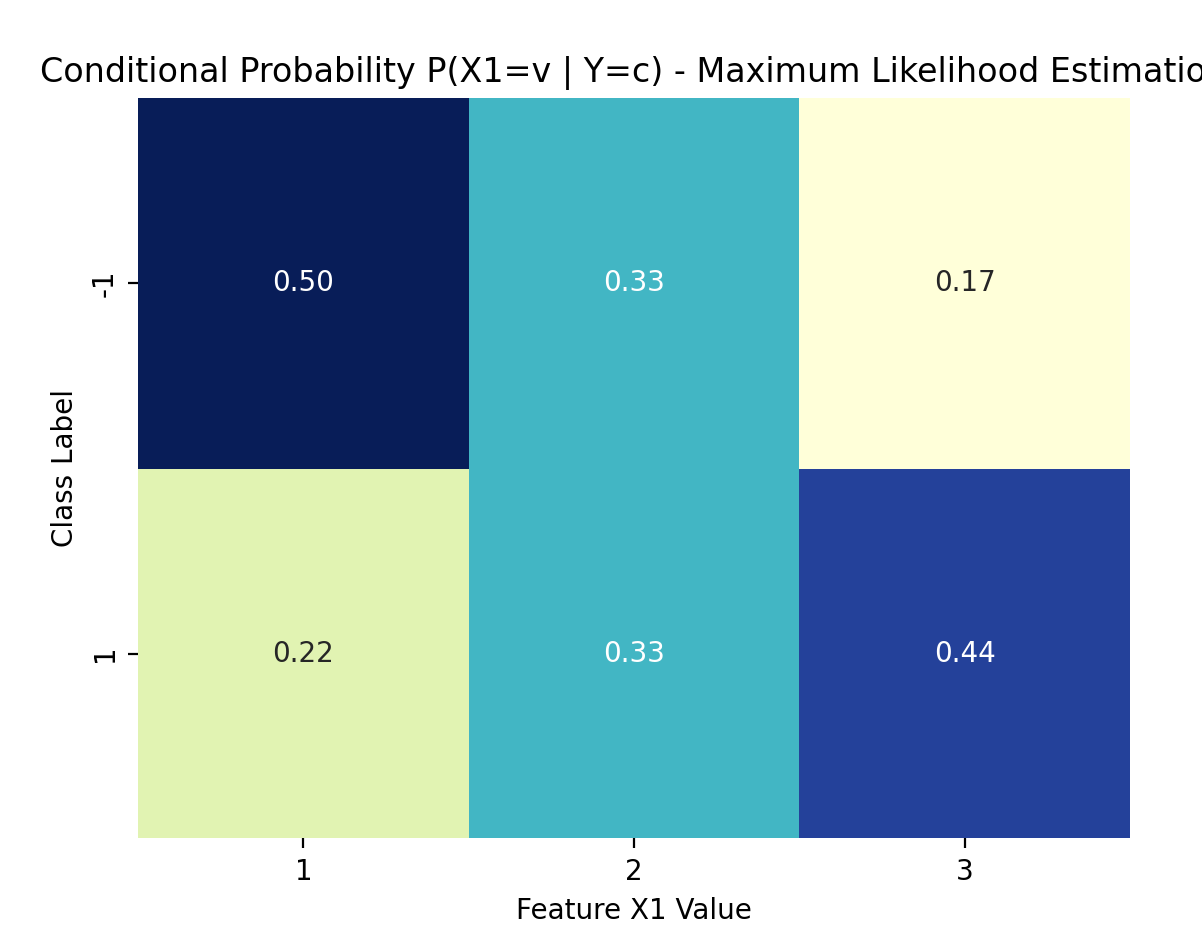
plot_cond_probs(nb_mle, 0, "Maximum Likelihood Estimation") # 特征X(1)
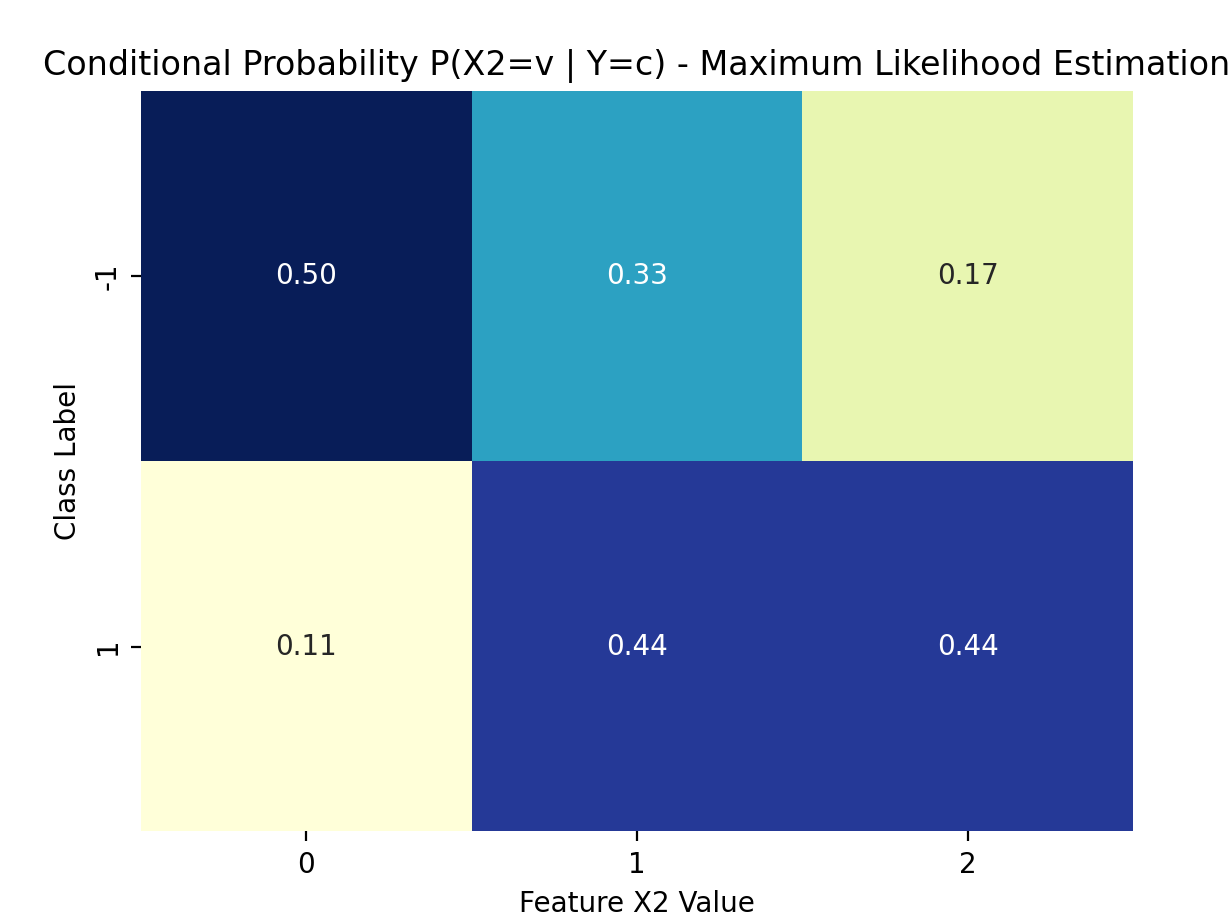
plot_cond_probs(nb_mle, 1, "Maximum Likelihood Estimation") # 特征X(2)
# 绘制两个特征的条件概率(贝叶斯估计)
plot_cond_probs(nb_bayes, 0, "Bayesian Estimation (Laplace Smoothing)") # 特征X(1)
plot_cond_probs(nb_bayes, 1, "Bayesian Estimation (Laplace Smoothing)") # 特征X(2)
# 3. 决策边界与分类区域
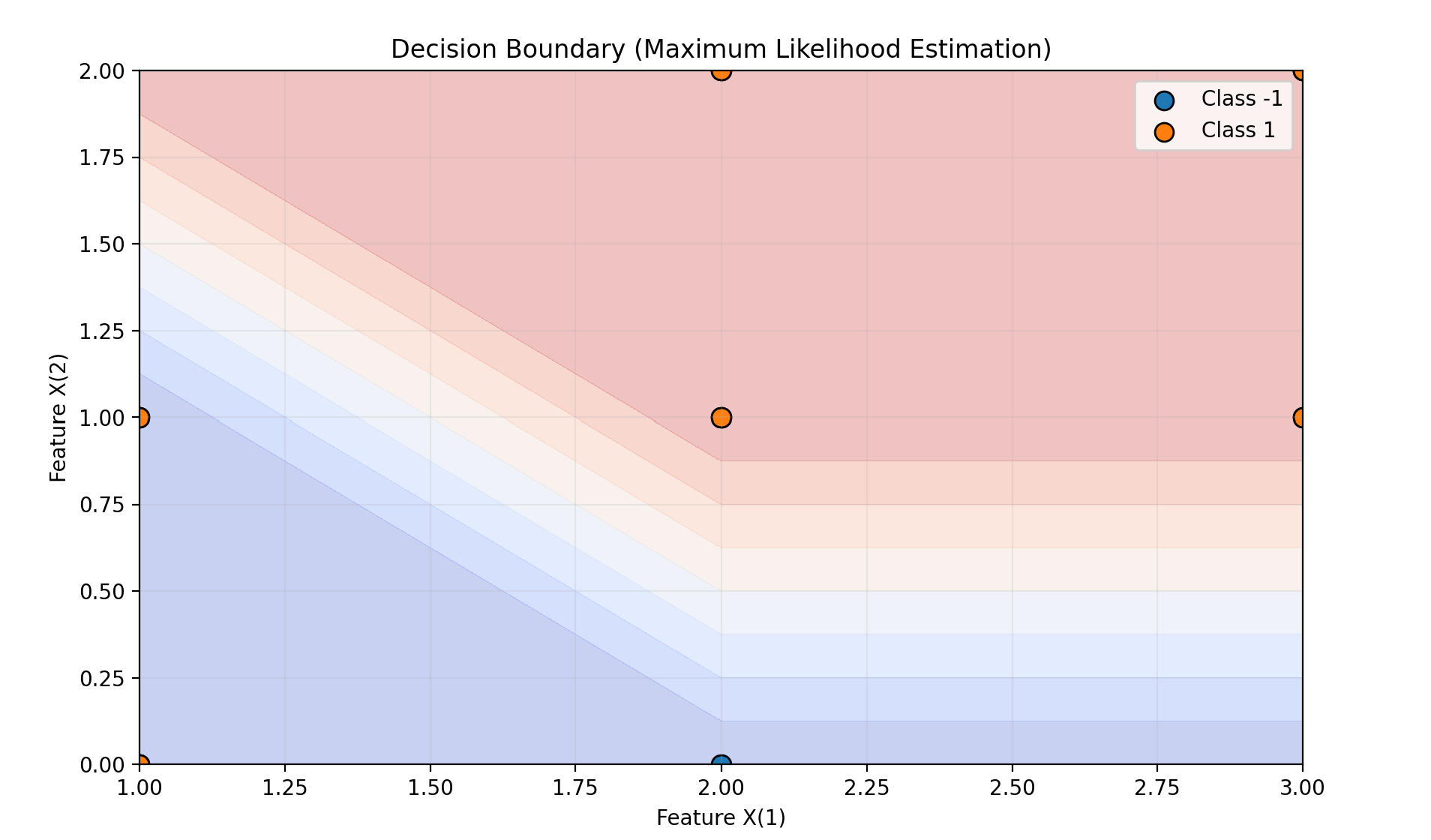
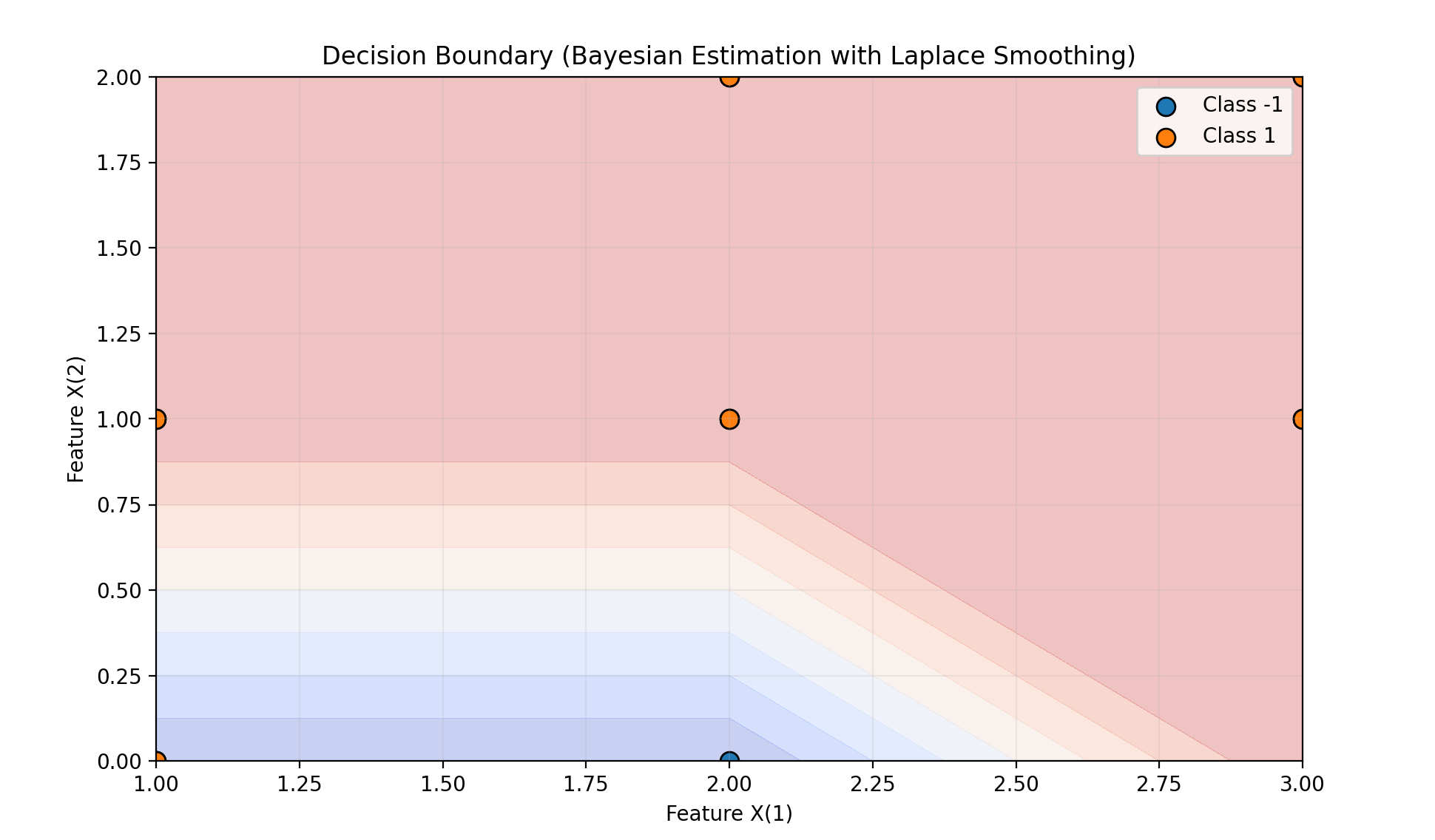
def plot_decision_boundary(nb, X, y, title):
"""绘制二维特征空间的决策边界与分类区域"""
# 获取特征的所有可能取值(构建网格用)
x1_vals = np.unique(X[:, 0])
x2_vals = np.unique(X[:, 1])
x1_grid, x2_grid = np.meshgrid(x1_vals, x2_vals)
grid_points = np.c_[x1_grid.ravel(), x2_grid.ravel()] # 网格所有点
# 预测网格中每个点的类别
grid_pred = nb.predict(grid_points).reshape(x1_grid.shape)
# 绘制分类区域(轮廓填充)
plt.figure(figsize=(10, 6))
plt.contourf(x1_grid, x2_grid, grid_pred, alpha=0.3, cmap="coolwarm")
# 绘制训练数据点(不同颜色表示类别)
for class_label in nb.classes:
idx = y == class_label
plt.scatter(X[idx, 0], X[idx, 1], label=f"Class {class_label}",
marker="o", s=80, edgecolors="black")
plt.title(title)
plt.xlabel("Feature X(1)")
plt.ylabel("Feature X(2)")
plt.legend()
plt.grid(alpha=0.2)
plt.show()
# 绘制两种估计的决策边界
plot_decision_boundary(nb_mle, X, y, "Decision Boundary (Maximum Likelihood Estimation)")
plot_decision_boundary(nb_bayes, X, y, "Decision Boundary (Bayesian Estimation with Laplace Smoothing)")
# 4. 混淆矩阵(模型分类效果评估)
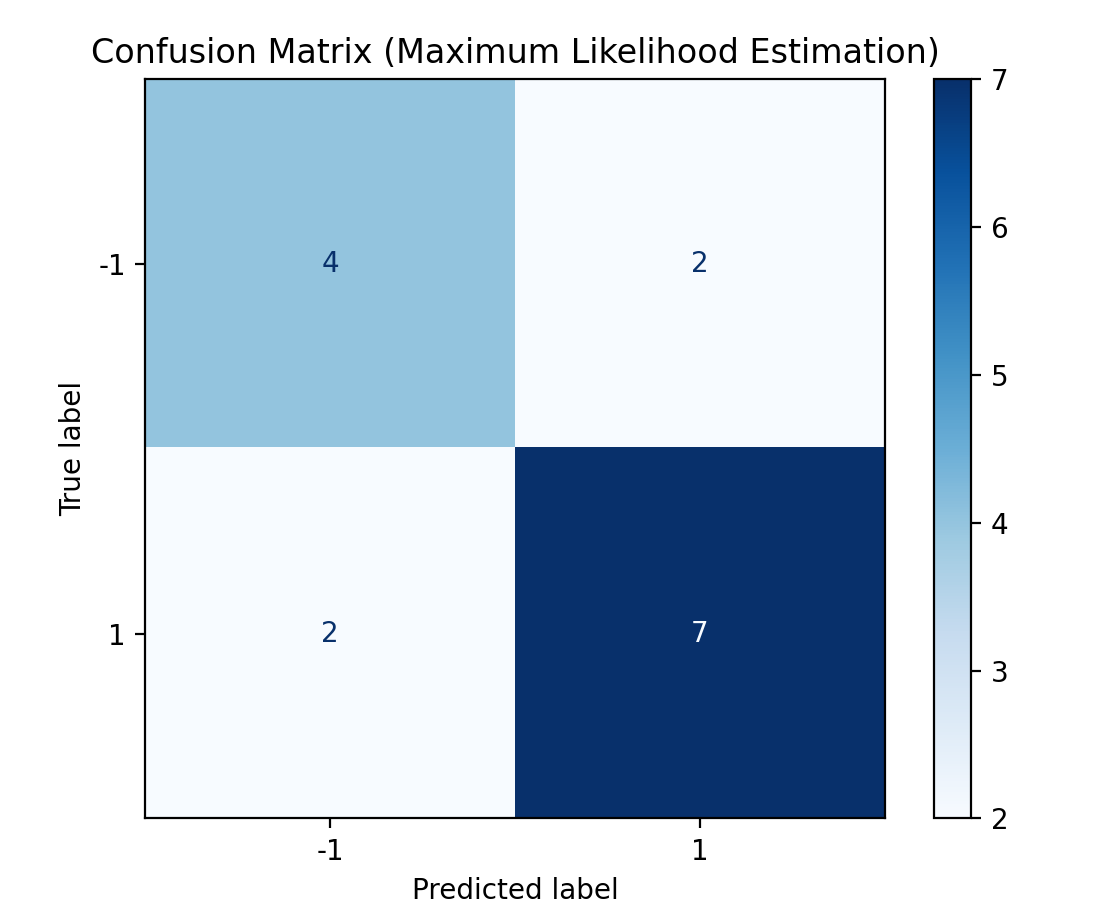
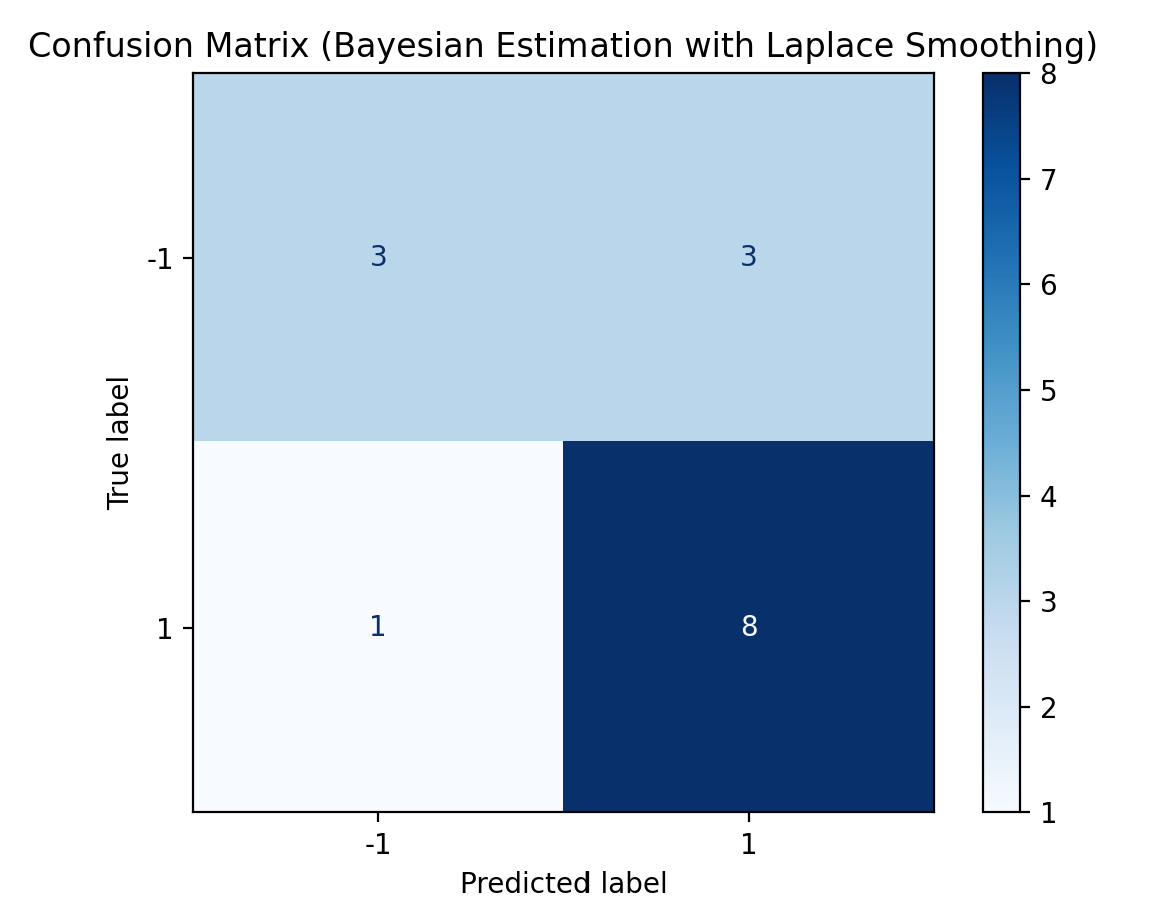
def plot_confusion_matrix(nb, X, y, title):
"""绘制混淆矩阵,评估模型在训练集上的分类效果"""
y_pred = nb.predict(X)
cm = confusion_matrix(y, y_pred)
disp = ConfusionMatrixDisplay(
confusion_matrix=cm,
display_labels=nb.classes
)
disp.plot(cmap=plt.cm.Blues, values_format="d")
plt.title(title)
plt.show()
# 绘制两种估计的混淆矩阵
plot_confusion_matrix(nb_mle, X, y, "Confusion Matrix (Maximum Likelihood Estimation)")
plot_confusion_matrix(nb_bayes, X, y, "Confusion Matrix (Bayesian Estimation with Laplace Smoothing)")程序运行结果如下:
极大似然估计预测结果: [-1]
贝叶斯估计(拉普拉斯平滑)预测结果: [-1]
=== 极大似然估计(Laplace λ=0)的概率计算 ===
- 先验概率:
P(Y=-1) = 0.4000
P(Y=1) = 0.6000
- 特征X(1)的条件概率 P(X(1)=v | Y=c):
P(X(1)=1 | Y=-1) = 0.5000
P(X(1)=2 | Y=-1) = 0.3333
P(X(1)=3 | Y=-1) = 0.1667
P(X(1)=1 | Y=1) = 0.2222
P(X(1)=2 | Y=1) = 0.3333
P(X(1)=3 | Y=1) = 0.4444
- 特征X(2)的条件概率 P(X(2)=v | Y=c):
P(X(2)=0 | Y=-1) = 0.5000
P(X(2)=1 | Y=-1) = 0.3333
P(X(2)=2 | Y=-1) = 0.1667
P(X(2)=0 | Y=1) = 0.1111
P(X(2)=1 | Y=1) = 0.4444
P(X(2)=2 | Y=1) = 0.4444
- 测试样本 x=(2, S)(编码为[2, 0])的后验分数:
P(Y=1) * P(X(1)=2|Y=1) * P(X(2)=0|Y=1) = 0.0222 (精确值:9/15 * 3/9 * 1/9 = 0.0222)
P(Y=-1) * P(X(1)=2|Y=-1) * P(X(2)=0|Y=-1) = 0.0667 (精确值:6/15 * 2/6 * 3/6 = 0.0667)
因为 0.0667 > 0.0222,所以预测类别: -1
=== 贝叶斯估计(拉普拉斯平滑 λ=1)的概率计算 ===
- 先验概率:
P(Y=-1) = 0.4118
P(Y=1) = 0.5882
- 特征X(1)的条件概率 P(X(1)=v | Y=c):
P(X(1)=1 | Y=-1) = 0.4444
P(X(1)=2 | Y=-1) = 0.3333
P(X(1)=3 | Y=-1) = 0.2222
P(X(1)=1 | Y=1) = 0.2500
P(X(1)=2 | Y=1) = 0.3333
P(X(1)=3 | Y=1) = 0.4167
- 特征X(2)的条件概率 P(X(2)=v | Y=c):
P(X(2)=0 | Y=-1) = 0.4444
P(X(2)=1 | Y=-1) = 0.3333
P(X(2)=2 | Y=-1) = 0.2222
P(X(2)=0 | Y=1) = 0.1667
P(X(2)=1 | Y=1) = 0.4167
P(X(2)=2 | Y=1) = 0.4167
- 测试样本 x=(2, S)(编码为[2, 0])的后验分数:
P(Y=1) * P(X(1)=2|Y=1) * P(X(2)=0|Y=1) = 0.0327 (精确值:10/17 * 4/12 * 2/12 = 0.0327 ≈ 0.0327)
P(Y=-1) * P(X(1)=2|Y=-1) * P(X(2)=0|Y=-1) = 0.0610 (精确值:7/17 * 3/9 * 4/9 = 0.0610 ≈ 0.0610)
因为 0.0610 > 0.0327,所以预测类别: -1
六、总结
-
朴素贝叶斯是生成学习方法:通过训练数据学习联合概率 P(X,Y)=P(Y)P(X∣Y),再求后验概率 P(Y∣X);概率估计可用极大似然或贝叶斯估计。
-
核心假设是条件独立性 :
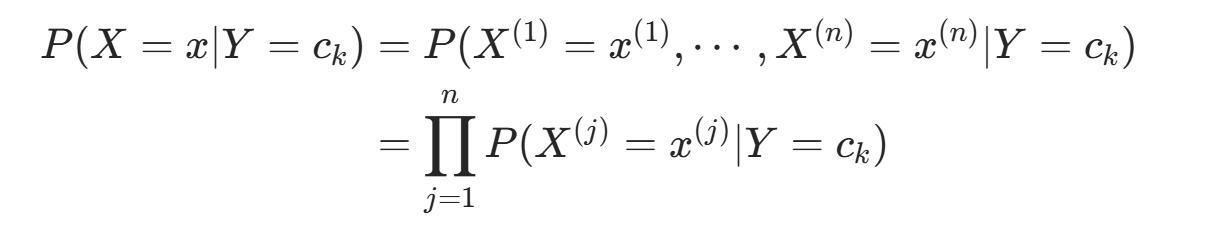 该假设简化了模型,但可能降低分类性能。
该假设简化了模型,但可能降低分类性能。 -
分类依据贝叶斯定理 :
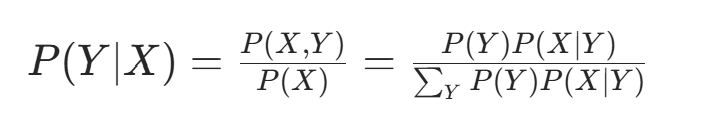 后验概率最大化等价于 0-1 损失下的期望风险最小化。
后验概率最大化等价于 0-1 损失下的期望风险最小化。