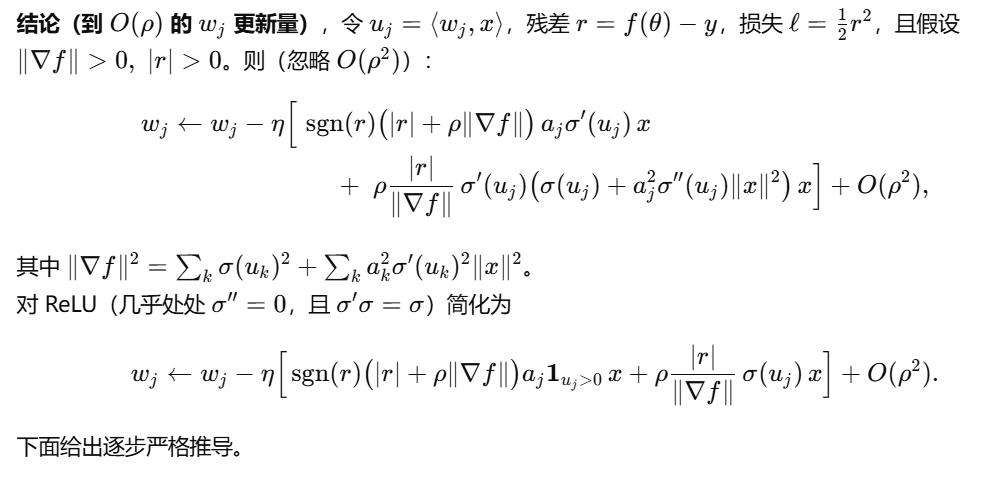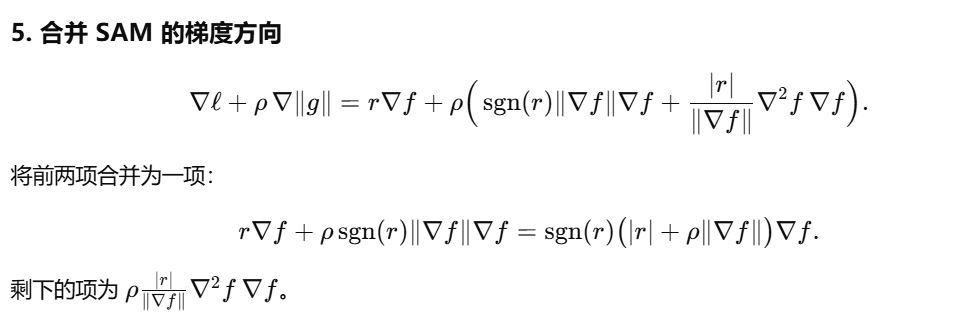SAM的低秩特性

锐度感知最小化（SAM）背景知识

设Itrain={1,...,n}I_{train} = \{1, ..., n\}Itrain={1,...,n}为训练集{xi,yi}i=1n\{x_i, y_i\}_{i=1}^n{xi,yi}i=1n的索引，ℓi(θ)\ell_i(\theta)ℓi(θ)为由权重θ∈R∣θ∣\theta \in \mathbb{R}^{|\theta|}θ∈R∣θ∣参数化的模型在数据点(xi,yi)(x_i, y_i)(xi,yi)上的损失。

SAM目标函数：min⁡θ∈R∣θ∣EI⊂Itrainmax⁡∥ε∥2≤ρ1∣I∣∑i∈Iℓi(θ+ε) \text{SAM目标函数：} \min {\theta \in \mathbb{R}^{|\theta|}} \underset{\mathcal{I} \subset \mathcal{I}{train }}{\mathbb{E}} \max _{\|\varepsilon\|2 \leq \rho} \frac{1}{|\mathcal{I}|} \sum{i \in \mathcal{I}} \ell_i(\theta+\varepsilon) SAM目标函数：θ∈R∣θ∣minI⊂ItrainE∥ε∥2≤ρmax∣I∣1i∈I∑ℓi(θ+ε)

其中I\mathcal{I}I是包含mmm个训练点的随机子集。需要说明的是，该目标函数基于对每个包含mmm个数据点的批次的损失和进行最大化。为了让SAM具备实用性，Foret等人（2021）提出使用随机梯度来最小化目标函数（1）。记ttt时刻的批次索引为It\mathcal{I}_tIt，则训练的每一轮迭代更新规则如下：

SAM更新规则：θt+1:=θt−γt∣It∣∑i∈It∇ℓi(θt+ρt∣It∣∑j∈It∇ℓj(θt)) \text{SAM更新规则：} \theta_{t+1} := \theta_t - \frac{\gamma_t}{|\mathcal{I}t|} \sum{i \in \mathcal{I}_t} \nabla \ell_i\left(\theta_t + \frac{\rho_t}{|\mathcal{I}t|} \sum{j \in \mathcal{I}_t} \nabla \ell_j(\theta_t)\right) SAM更新规则：θt+1:=θt−∣It∣γti∈It∑∇ℓi θt+∣It∣ρtj∈It∑∇ℓj(θt)

需要注意的是，内梯度步和外梯度步使用了相同的批次It\mathcal{I}_tIt，且ρt\rho_tρt通常包含梯度归一化，即ρt:=ρ/∥1∣It∣∑j∈It∇ℓj(θt)∥2\rho_t := \rho / \left\|\frac{1}{|\mathcal{I}t|} \sum{j \in \mathcal{I}_t} \nabla \ell_j(\theta_t)\right\|_2ρt:=ρ/ ∣It∣1∑j∈It∇ℓj(θt) 2。正如Foret等人（2021）所指出的，SAM中的最坏情况扰动以及小批次规模mmm，是泛化性能提升的关键因素，且泛化性能随mmm的变化呈连续趋势。

低秩特性

有研究发现在过度参数化的神经网络上进行锐度感知最小化会产生低秩特征。

为什么SAM会诱导低秩特性或者说SAM如何诱导低秩特性呢，我们继续来看看

理论分析选择 "双层 ReLU 网络" 作为研究载体 （这是深度学习中最简单的非线性网络结构之一），背景是：简单模型的参数空间、激活机制更透明，便于推导数学关系，且其结论可为理解深层网络的机制提供基础。

在理论分析前，研究者已对双层 ReLU 网络进行了初步实验，发现了一个关键现象：SAM 导致的低秩特征与 "激活单元被完全剪枝" 直接相关。具体来说，随着 SAM 的扰动参数 ρ 增大，网络中 "活跃的 ReLU 单元" 数量显著减少，而大量零激活单元直接降低了特征矩阵的秩。

令ℓ(θ)\ell(\theta)ℓ(θ)为随机梯度下降（SGD）采样到的样本 (x,y)(x, y)(x,y) 上的损失，并具体假设采用平方损失。我们将理论论证表述为如下命题：

命题1

在采用平方损失训练的双层ReLU网络中，SAM的每一次更新均包含一个组件：该组件会使所有预激活值<wj,x>j=1m{< w_{j}, x>}{j=1}^{m}<wj,x>j=1m降低，降低的幅度为非负值，具体等于ηρℓ(θ)/∥∇f(θ)∥2σ(<wj,x>)∥x∥22\eta \rho \sqrt{\ell(\theta)} /\|\nabla f(\theta)\|{2} \sigma(<w_{j}, x>)\|x\|_{2}^{2}ηρℓ(θ) /∥∇f(θ)∥2σ(<wj,x>)∥x∥22

现在来解释这个命题：

在解释命题前，先回顾2个关键术语（基于前文双层ReLU网络的定义）：

预激活值（pre-activation value） ：指隐藏层神经元在经过ReLU激活前的输入，即第jjj个神经元的预激活值为⟨wj,x⟩\langle w_j, x \rangle⟨wj,x⟩ ,wjw_jwj是隐藏层第jjj个神经元的权重向量，xxx是输入数据）。

它直接决定神经元是否"激活"：若⟨wj,x⟩>0\langle w_j, x \rangle > 0⟨wj,x⟩>0，ReLU输出sigma(⟨wj,x⟩)=⟨wj,x⟩sigma(\langle w_j, x \rangle) = \langle w_j, x \ranglesigma(⟨wj,x⟩)=⟨wj,x⟩（神经元活跃）；若⟨wj,x⟩≤0\langle w_j, x \rangle \leq 0⟨wj,x⟩≤0，ReLU输出0（神经元"躺平"，被剪枝）。
SAM的更新本质：SAM不是直接用当前参数的梯度更新，而是先给参数加一个"最坏情况的小扰动"，再用扰动后参数的梯度更新（目的是找"平坦最小值"）。命题聚焦的是：这个更新过程里，藏着一个专门"压低预激活值"的组件。

对于SAM的更新，我们有如下推导：
∇ℓ(θ+ρ⋅∇ℓ(θ)∥∇ℓ(θ)∥2)=∇ℓ(θ)+ρ⋅∇2ℓ(θ)⋅∇ℓ(θ)∥∇ℓ(θ)∥2+O(ρ2)=∇[ℓ(θ)+ρ∥∇ℓ(θ)∥2+O(ρ2)] \nabla\ell\left( \theta + \rho \cdot \frac{\nabla\ell(\theta)}{\|\nabla\ell(\theta)\|_2} \right) = \nabla\ell(\theta) + \rho \cdot \nabla^2\ell(\theta) \cdot \frac{\nabla\ell(\theta)}{\|\nabla\ell(\theta)\|_2} + \mathcal{O}(\rho^2) = \nabla\left[ \ell(\theta) + \rho\|\nabla\ell(\theta)\|_2 + \mathcal{O}(\rho^2) \right] ∇ℓ(θ+ρ⋅∥∇ℓ(θ)∥2∇ℓ(θ))=∇ℓ(θ)+ρ⋅∇2ℓ(θ)⋅∥∇ℓ(θ)∥2∇ℓ(θ)+O(ρ2)=∇[ℓ(θ)+ρ∥∇ℓ(θ)∥2+O(ρ2)]

因此，在一阶泰勒近似 （忽略O(ρ2)\mathcal{O}(\rho^2)O(ρ2)高阶小项）下，SAM的一步更新等价于对正则化目标函数 ℓ(θ)+ρ∥∇ℓ(θ)∥2\ell(\theta) + \rho\|\nabla\ell(\theta)\|_2ℓ(θ)+ρ∥∇ℓ(θ)∥2进行梯度更新。

接下来回顾双层网络的层级梯度（即网络各层参数的梯度）定义：

对于前文定义的双层ReLU网络（输入→隐藏层ReLU激活→输出层内积），其损失关于网络参数的梯度（即层级梯度）可表示为：

∇aℓ(θ)=ℓ′(θ)⋅σ(Wx),∇wjℓ(θ)=ℓ′(θ)⋅ajσ′(⟨wj,x⟩)x \nabla {a}\ell (\theta )=\ell ^{\prime }(\theta )\cdot \sigma (Wx), \quad \nabla {w{j}}\ell (\theta )=\ell ^{\prime }(\theta )\cdot a{j}\sigma ^{\prime }(\langle w_{j},x \rangle )x ∇aℓ(θ)=ℓ′(θ)⋅σ(Wx),∇wjℓ(θ)=ℓ′(θ)⋅ajσ′(⟨wj,x⟩)x

符号含义说明（结合网络结构）

∇aℓ(θ)\nabla _{a}\ell (\theta )∇aℓ(θ) ：损失ℓ(θ)\ell(\theta)ℓ(θ)关于输出层权重向量aaa 的梯度，维度与aaa一致（Rm\mathbb{R}^mRm，mmm为隐藏层神经元数量），对应输出层参数的更新方向。
∇wjℓ(θ)\nabla {w{j}}\ell (\theta )∇wjℓ(θ) ：损失ℓ(θ)\ell(\theta)ℓ(θ)关于隐藏层第jjj个神经元权重向量wjw_jwj 的梯度，维度与wjw_jwj一致（Rd\mathbb{R}^dRd，ddd为输入维度），对应隐藏层单个神经元参数的更新方向。
ℓ′(θ)\ell ^{\prime }(\theta )ℓ′(θ) ：损失ℓ(θ)\ell(\theta)ℓ(θ)关于网络输出 的导数（标量），对于平方损失ℓ(θ)=12(f(θ;x)−y)2\ell(\theta)=\frac{1}{2}(f(\theta;x)-y)^2ℓ(θ)=21(f(θ;x)−y)2，其值为ℓ′(θ)=f(θ;x)−y\ell ^{\prime }(\theta)=f(\theta;x)-yℓ′(θ)=f(θ;x)−y（即预测值与真实标签的残差）。
σ(Wx)\sigma (Wx)σ(Wx) ：隐藏层的ReLU激活向量 （Rm\mathbb{R}^mRm），其中WWW为隐藏层权重矩阵（Rm×d\mathbb{R}^{m \times d}Rm×d），xxx为输入向量（Rd\mathbb{R}^dRd），σ(⋅)\sigma(\cdot)σ(⋅)为ReLU函数（σ(z)=max⁡(z,0)\sigma(z)=\max(z,0)σ(z)=max(z,0)）。
aja_jaj ：输出层权重向量aaa的第jjj个元素（标量），对应隐藏层第jjj个神经元与输出层的连接权重。
σ′(⟨wj,x⟩)\sigma ^{\prime }(\langle w_{j},x \rangle )σ′(⟨wj,x⟩) ：ReLU函数关于隐藏层第jjj个神经元预激活值 的导数（标量），ReLU导数定义为σ′(z)={1,z>00,z≤0\sigma ^{\prime }(z)=\begin{cases}1, & z>0 \\ 0, & z \leq 0\end{cases}σ′(z)={1,0,z>0z≤0（几乎处处成立）。
⟨wj,x⟩\langle w_{j},x \rangle⟨wj,x⟩ ：隐藏层第jjj个神经元的预激活值 （标量），即权重向量wjw_jwj与输入xxx的内积，决定该神经元是否被激活。

核心是顺着「全梯度范数计算→SAM权重更新拆解→预激活值变化」的逻辑链展开，每个公式都建立在之前的层级梯度、泰勒展开结论（SAM等价于正则化目标）和ReLU特性之上。以下分三部分解释：

一、第一步：全梯度范数的表达式推导（从"残差"到"根号内两项"）

1. 第一层等价：∥∇ℓ(θ)∥2=∣r∣⋅∥∇f(θ)∥2\|\nabla \ell(\theta)\|_2 = |r| \cdot \|\nabla f(\theta)\|_2∥∇ℓ(θ)∥2=∣r∣⋅∥∇f(θ)∥2

符号定义 ：r=f(θ;x)−yr = f(\theta;x) - yr=f(θ;x)−y（模型输出与真实标签的「残差」，标量），ℓ(θ)=12r2\ell(\theta) = \frac{1}{2}r^2ℓ(θ)=21r2（平方损失）。
核心逻辑 ：损失ℓ\ellℓ是模型输出fff的函数（ℓ=12(f−y)2\ell = \frac{1}{2}(f-y)^2ℓ=21(f−y)2），根据链式法则 ，损失的梯度∇ℓ(θ)\nabla \ell(\theta)∇ℓ(θ)与模型输出的梯度∇f(θ)\nabla f(\theta)∇f(θ)满足：
∇ℓ(θ)=dℓdf⋅∇f(θ)=r⋅∇f(θ)\nabla \ell(\theta) = \frac{d\ell}{df} \cdot \nabla f(\theta) = r \cdot \nabla f(\theta)∇ℓ(θ)=dfdℓ⋅∇f(θ)=r⋅∇f(θ)
（因为dℓdf=f−y=r\frac{d\ell}{df} = f - y = rdfdℓ=f−y=r）。
范数性质 ：对等式两边取L2范数，因范数满足∥k⋅v∥2=∣k∣⋅∥v∥2\|k \cdot v\|_2 = |k| \cdot \|v\|_2∥k⋅v∥2=∣k∣⋅∥v∥2（kkk为标量，vvv为向量），故：
∥∇ℓ(θ)∥2=∣r∣⋅∥∇f(θ)∥2\|\nabla \ell(\theta)\|_2 = |r| \cdot \|\nabla f(\theta)\|_2∥∇ℓ(θ)∥2=∣r∣⋅∥∇f(θ)∥2

2. 第二层等价：∥∇f(θ)∥2\|\nabla f(\theta)\|_2∥∇f(θ)∥2展开为根号内两项

∇f(θ)\nabla f(\theta)∇f(θ)是「模型输出fff关于所有参数θ\thetaθ的梯度」，而θ=[vec(W),a]\theta = [\text{vec}(W), a]θ=[vec(W),a]（隐藏层权重WWW+输出层权重aaa），因此∇f(θ)\nabla f(\theta)∇f(θ)是一个向量，包含两部分：

对输出层权重aaa的偏导：∇af(θ)=σ(Wx)\nabla_a f(\theta) = \sigma(Wx)∇af(θ)=σ(Wx)（因f=⟨a,σ(Wx)⟩f = \langle a, \sigma(Wx) \ranglef=⟨a,σ(Wx)⟩，对aaa求偏导即σ(Wx)\sigma(Wx)σ(Wx)）；
对隐藏层第jjj个神经元权重wjw_jwj的偏导：∇wjf(θ)=aj⋅σ′(⟨wj,x⟩)⋅x\nabla_{w_j} f(\theta) = a_j \cdot \sigma'(\langle w_j, x \rangle) \cdot x∇wjf(θ)=aj⋅σ′(⟨wj,x⟩)⋅x（链式法则：fff对wjw_jwj的偏导 = 对σ(Wx)j\sigma(Wx)_jσ(Wx)j的偏导 × σ(Wx)j\sigma(Wx)_jσ(Wx)j对wjw_jwj的偏导）。

根据L2范数的定义（向量各元素平方和的平方根），∥∇f(θ)∥22\|\nabla f(\theta)\|_2^2∥∇f(θ)∥22（范数的平方）等于两部分偏导的范数平方和：
∥∇f(θ)∥22=∥∇af(θ)∥22+∑j=1m∥∇wjf(θ)∥22\|\nabla f(\theta)\|2^2 = \|\nabla_a f(\theta)\|2^2 + \sum{j=1}^m \|\nabla{w_j} f(\theta)\|_2^2∥∇f(θ)∥22=∥∇af(θ)∥22+j=1∑m∥∇wjf(θ)∥22

代入偏导表达式：

第一部分：∥∇af(θ)∥22=∥σ(Wx)∥22\|\nabla_a f(\theta)\|_2^2 = \|\sigma(Wx)\|_2^2∥∇af(θ)∥22=∥σ(Wx)∥22；
第二部分：∑j=1m∥∇wjf(θ)∥22=∑j=1m∥ajσ′(⟨wj,x⟩)x∥22\sum_{j=1}^m \|\nabla_{w_j} f(\theta)\|2^2 = \sum{j=1}^m \left\| a_j \sigma'(\langle w_j, x \rangle) x \right\|_2^2∑j=1m∥∇wjf(θ)∥22=∑j=1m∥ajσ′(⟨wj,x⟩)x∥22。
因∥k⋅v∥22=k2⋅∥v∥22\|k \cdot v\|_2^2 = k^2 \cdot \|v\|_2^2∥k⋅v∥22=k2⋅∥v∥22，且xxx与jjj无关，可提取公因子∥x∥22\|x\|2^2∥x∥22：
∑j=1maj2σ′(⟨wj,x⟩)2⋅∥x∥22=∥x∥22⋅∥a⊙σ′(Wx)∥22\sum{j=1}^m a_j^2 \sigma'(\langle w_j, x \rangle)^2 \cdot \|x\|_2^2 = \|x\|_2^2 \cdot \left\| a \odot \sigma'(Wx) \right\|2^2j=1∑maj2σ′(⟨wj,x⟩)2⋅∥x∥22=∥x∥22⋅∥a⊙σ′(Wx)∥22
（⊙\odot⊙是「元素-wise乘法」，a⊙σ′(Wx)a \odot \sigma'(Wx)a⊙σ′(Wx)的第jjj个元素为ajσ′(⟨wj,x⟩)a_j \sigma'(\langle w_j, x \rangle)ajσ′(⟨wj,x⟩)，其范数平方即∑j=1maj2σ′(⟨wj,x⟩)2\sum{j=1}^m a_j^2 \sigma'(\langle w_j, x \rangle)^2∑j=1maj2σ′(⟨wj,x⟩)2）。

因此，∥∇f(θ)∥2=∥σ(Wx)∥22+∥x∥22⋅∥a⊙σ′(Wx)∥22\|\nabla f(\theta)\|_2 = \sqrt{\|\sigma(Wx)\|_2^2 + \|x\|_2^2 \cdot \left\| a \odot \sigma'(Wx) \right\|_2^2}∥∇f(θ)∥2=∥σ(Wx)∥22+∥x∥22⋅∥a⊙σ′(Wx)∥22 ，代入第一层等价关系，最终得到全梯度范数：
∥∇ℓ(θ)∥2=∣r∣⋅∥σ(Wx)∥22+∥x∥22⋅∥a⊙σ′(Wx)∥22\|\nabla \ell(\theta)\|_2 = |r| \cdot \sqrt{\|\sigma(Wx)\|_2^2 + \|x\|_2^2 \cdot \left\| a \odot \sigma'(Wx) \right\|_2^2}∥∇ℓ(θ)∥2=∣r∣⋅∥σ(Wx)∥22+∥x∥22⋅∥a⊙σ′(Wx)∥22

二、第二步：SAM对隐藏层权重wjw_jwj的更新拆解

这部分是将SAM的更新规则（基于正则化目标）具体到隐藏层单个神经元的权重wjw_jwj，并拆分为「数据拟合项」和「正则化项」。

1. SAM更新的基础形式

根据前文泰勒展开结论：SAM的更新等价于对正则化目标ℓ(θ)+ρ∥∇ℓ(θ)∥2\ell(\theta) + \rho \|\nabla \ell(\theta)\|_2ℓ(θ)+ρ∥∇ℓ(θ)∥2的梯度更新 （忽略O(ρ2)\mathcal{O}(\rho^2)O(ρ2)高阶小项）。

正则化目标的梯度为∇[ℓ(θ)+ρ∥∇ℓ(θ)∥2]=∇ℓ(θ)+ρ∇∥∇ℓ(θ)∥2\nabla \left[ \ell(\theta) + \rho \|\nabla \ell(\theta)\|_2 \right] = \nabla \ell(\theta) + \rho \nabla \|\nabla \ell(\theta)\|_2∇[ℓ(θ)+ρ∥∇ℓ(θ)∥2]=∇ℓ(θ)+ρ∇∥∇ℓ(θ)∥2。

因此，学习率为η\etaη时，隐藏层第jjj个神经元的权重wjw_jwj更新公式为：
wj:=wj−η⋅(∇ℓ(θ)+ρ∇∥∇ℓ(θ)∥2)+O(ρ2)w_j := w_j - \eta \cdot \left( \nabla \ell(\theta) + \rho \nabla \|\nabla \ell(\theta)\|_2 \right) + \mathcal{O}(\rho^2)wj:=wj−η⋅(∇ℓ(θ)+ρ∇∥∇ℓ(θ)∥2)+O(ρ2)

2. 拆分为"数据拟合项"与"正则化项"

核心是代入「层级梯度」（对wjw_jwj的损失梯度）和「全梯度范数关系」，结合ReLU特性化简（论文中间省略了很多步骤，具体证明见附录）：

数据拟合项（Data Fitting Term） ：

来自∇ℓ(θ)\nabla \ell(\theta)∇ℓ(θ)中对wjw_jwj的梯度部分。根据前文层级梯度公式，∇wjℓ(θ)=r⋅aj⋅σ′(⟨wj,x⟩)⋅x\nabla_{w_j} \ell(\theta) = r \cdot a_j \cdot \sigma'(\langle w_j, x \rangle) \cdot x∇wjℓ(θ)=r⋅aj⋅σ′(⟨wj,x⟩)⋅x（r=f−yr = f - yr=f−y是残差）。

再结合全梯度范数∥∇ℓ(θ)∥2=∣r∣⋅∥∇f(θ)∥2\|\nabla \ell(\theta)\|_2 = |r| \cdot \|\nabla f(\theta)\|_2∥∇ℓ(θ)∥2=∣r∣⋅∥∇f(θ)∥2，以及平方损失ℓ(θ)=12r2\ell(\theta) = \frac{1}{2}r^2ℓ(θ)=21r2（故ℓ(θ)=∣r∣2\sqrt{\ell(\theta)} = \frac{|r|}{\sqrt{2}}ℓ(θ) =2 ∣r∣，但推导中可直接用∥r∥=∥∇ℓ(θ)∥2∥∇f(θ)∥2\|r\| = \frac{\|\nabla \ell(\theta)\|_2}{\|\nabla f(\theta)\|_2}∥r∥=∥∇f(θ)∥2∥∇ℓ(θ)∥2），最终数据拟合项化简为：
ηr(1+ρ∥∇f(θ)∥2ℓ(θ))ajσ′(⟨wj,x⟩)x\eta r \left( 1 + \rho \frac{\|\nabla f(\theta)\|_2}{\sqrt{\ell(\theta)}} \right) a_j \sigma'(\langle w_j, x \rangle) xηr(1+ρℓ(θ) ∥∇f(θ)∥2)ajσ′(⟨wj,x⟩)x

它的作用与「普通梯度更新」一致（拟合训练数据），但多了一个系数(1+ρ∥∇f(θ)∥2ℓ(θ))\left( 1 + \rho \frac{\|\nabla f(\theta)\|_2}{\sqrt{\ell(\theta)}} \right)(1+ρℓ(θ) ∥∇f(θ)∥2)，相当于增大了有效学习率。
正则化项（Regularization Component） ：

来自ρ∇∥∇ℓ(θ)∥2\rho \nabla \|\nabla \ell(\theta)\|_2ρ∇∥∇ℓ(θ)∥2（SAM的核心正则化部分），通过代入全梯度范数关系和ReLU特性σ′(⟨wj,x⟩)σ(⟨wj,x⟩)=σ(⟨wj,x⟩)\sigma'(\langle w_j, x \rangle) \sigma(\langle w_j, x \rangle) = \sigma(\langle w_j, x \rangle)σ′(⟨wj,x⟩)σ(⟨wj,x⟩)=σ(⟨wj,x⟩)（因z>0z>0z>0时σ′(z)=1\sigma'(z)=1σ′(z)=1，乘积=σ(z)；z≤0z≤0z≤0时σ(z)=0，乘积=0），最终化简为：
ηρℓ(θ)∥∇f(θ)∥2σ(⟨wj,x⟩)x\eta \rho \frac{\sqrt{\ell(\theta)}}{\|\nabla f(\theta)\|_2} \sigma(\langle w_j, x \rangle) xηρ∥∇f(θ)∥2ℓ(θ) σ(⟨wj,x⟩)x

它是SAM独有的项，后续会证明其对「预激活值的压制作用」。

三、第三步：预激活值的更新------SAM如何"压低"神经元活性

预激活值⟨wj,x⟩\langle w_j, x \rangle⟨wj,x⟩是隐藏层神经元的"开关"（>0>0>0激活，≤0≤0≤0躺平）。这段推导的核心是证明：SAM的更新会让预激活值持续降低，且降低幅度非负。

1. 预激活值更新的推导逻辑

预激活值是wjw_jwj与xxx的内积（⟨wj,x⟩=wj⊤x\langle w_j, x \rangle = w_j^\top x⟨wj,x⟩=wj⊤x）。当wjw_jwj更新为wj′=wj−Δwjw_j' = w_j - \Delta w_jwj′=wj−Δwj（Δwj\Delta w_jΔwj是更新量）时，新的预激活值为：
⟨wj′,x⟩=⟨wj−Δwj,x⟩=⟨wj,x⟩−⟨Δwj,x⟩\langle w_j', x \rangle = \langle w_j - \Delta w_j, x \rangle = \langle w_j, x \rangle - \langle \Delta w_j, x \rangle⟨wj′,x⟩=⟨wj−Δwj,x⟩=⟨wj,x⟩−⟨Δwj,x⟩

而Δwj=数据拟合项+正则化项\Delta w_j = \text{数据拟合项} + \text{正则化项}Δwj=数据拟合项+正则化项（来自第二步的更新公式），因此：
⟨wj′,x⟩=⟨wj,x⟩−⟨数据拟合项,x⟩−⟨正则化项,x⟩+O(ρ2)\langle w_j', x \rangle = \langle w_j, x \rangle - \langle \text{数据拟合项}, x \rangle - \langle \text{正则化项}, x \rangle + \mathcal{O}(\rho^2)⟨wj′,x⟩=⟨wj,x⟩−⟨数据拟合项,x⟩−⟨正则化项,x⟩+O(ρ2)

2. 代入两项的内积计算

对「数据拟合项」：⟨数据拟合项,x⟩=ηr(1+ρ∥∇f(θ)∥2ℓ(θ))ajσ′(⟨wj,x⟩)⋅∥x∥22\langle \text{数据拟合项}, x \rangle = \eta r \left( 1 + \rho \frac{\|\nabla f(\theta)\|_2}{\sqrt{\ell(\theta)}} \right) a_j \sigma'(\langle w_j, x \rangle) \cdot \|x\|_2^2⟨数据拟合项,x⟩=ηr(1+ρℓ(θ) ∥∇f(θ)∥2)ajσ′(⟨wj,x⟩)⋅∥x∥22

（因⟨k⋅x,x⟩=k⋅∥x∥22\langle k \cdot x, x \rangle = k \cdot \|x\|_2^2⟨k⋅x,x⟩=k⋅∥x∥22，数据拟合项中含因子xxx）。
对「正则化项」：⟨正则化项,x⟩=ηρℓ(θ)∥∇f(θ)∥2σ(⟨wj,x⟩)⋅∥x∥22\langle \text{正则化项}, x \rangle = \eta \rho \frac{\sqrt{\ell(\theta)}}{\|\nabla f(\theta)\|_2} \sigma(\langle w_j, x \rangle) \cdot \|x\|_2^2⟨正则化项,x⟩=ηρ∥∇f(θ)∥2ℓ(θ) σ(⟨wj,x⟩)⋅∥x∥22

（同理，正则化项中含因子xxx）。

代入后得到预激活值的更新公式：
⟨wj,x⟩:=⟨wj,x⟩−ηr(1+ρ∥∇f(θ)∥2ℓ(θ))ajσ′(⟨wj,x⟩)∥x∥22−ηρℓ(θ)∥∇f(θ)∥2σ(⟨wj,x⟩)∥x∥22+O(ρ2)\begin{aligned} \langle w_j, x \rangle &:= \langle w_j, x \rangle - \eta r \left( 1 + \rho \frac{\|\nabla f(\theta)\|_2}{\sqrt{\ell(\theta)}} \right) a_j \sigma'(\langle w_j, x \rangle) \|x\|_2^2 \\ & \quad - \eta \rho \frac{\sqrt{\ell(\theta)}}{\|\nabla f(\theta)\|_2} \sigma(\langle w_j, x \rangle) \|x\|_2^2 + \mathcal{O}(\rho^2) \end{aligned}⟨wj,x⟩:=⟨wj,x⟩−ηr(1+ρℓ(θ) ∥∇f(θ)∥2)ajσ′(⟨wj,x⟩)∥x∥22−ηρ∥∇f(θ)∥2ℓ(θ) σ(⟨wj,x⟩)∥x∥22+O(ρ2)

3. 关键结论：正则化项导致预激活值"只降不升"

公式中第二项（正则化项带来的降低量）ηρℓ(θ)∥∇f(θ)∥2σ(⟨wj,x⟩)∥x∥22\eta \rho \frac{\sqrt{\ell(\theta)}}{\|\nabla f(\theta)\|_2} \sigma(\langle w_j, x \rangle) \|x\|_2^2ηρ∥∇f(θ)∥2ℓ(θ) σ(⟨wj,x⟩)∥x∥22 恒非负，原因是所有因子均非负：

η>0\eta > 0η>0（学习率为正）；
ρ>0\rho > 0ρ>0（SAM的扰动半径为正）；
ℓ(θ)≥0\sqrt{\ell(\theta)} \geq 0ℓ(θ) ≥0（损失非负）；
∥∇f(θ)∥2>0\|\nabla f(\theta)\|_2 > 0∥∇f(θ)∥2>0（训练中模型梯度不为零，否则停止更新）；
σ(⟨wj,x⟩)≥0\sigma(\langle w_j, x \rangle) \geq 0σ(⟨wj,x⟩)≥0（ReLU激活值非负）；
∥x∥22≥0\|x\|_2^2 \geq 0∥x∥22≥0（输入向量的范数平方非负）。

这意味着：SAM的正则化项会持续压低预激活值 ------对已激活的神经元（σ(⋅)>0\sigma(\cdot) > 0σ(⋅)>0），预激活值不断降低，可能跌破0导致神经元"躺平"（被剪枝）；对已躺平的神经元（σ(⋅)=0\sigma(\cdot) = 0σ(⋅)=0），降低量为0，不额外影响。这正是命题1的核心，也是SAM诱导低秩特征的底层机制。

SAM更新中仅使用一阶项，就能在特征秩、活跃ReLU数量等关键指标上产生与完整SAM相同的效果，这一机制说明SAM可抑制拟合训练数据无需的冗余激活，且该效果在SGD的每次迭代中均存在，因与损失平方根ℓ(θ)\sqrt{\ell(\theta)}ℓ(θ) 成正比，在训练初期表现更强；此外，类似逻辑适用于多层网络，由于∥∇f(θ)∥2\|\nabla f(\theta)\|_{2}∥∇f(θ)∥2包含所有层的激活，多层网络会出现低秩效应，同时这也为SAM平坦最小值提供了直观解释，即其对应在训练数据上激活稀疏的网络。