例题:洛谷P2742【模板】二维凸包
更适合初学者体质的题解。
1.凸包介绍
在平面上能包含所有给定点的最小凸多边形叫做凸包。
根据三角不等式,凸包也一定是包含所有给定点的周长最小多边形。
同样可以理解为,我们在地上钉了一些钉子,有一个有弹性皮筋,我们把它拉大框住所有钉子,然后松手,皮筋的形状就是凸包。
上凸壳(qiao or ke?)一般指凸包的上半部分,看完本篇题解应该会有更深刻的理解。
显然,这个题目求的是凸包的周长。
2.Andrew 算法介绍
一个求凸包的算法,或许也叫安德鲁算法?
我们先按照横坐标为第一关键字,纵坐标为第二关键字,从小到大排序。显然,第一个点和最后一个点一定在凸包上。
我们先考虑求上凸壳,下凸壳同理。
在排好序的点中从小到大枚举,加入一个新点 c c c 时,如果形成了凹多边形(如下图),那么不合法,依照三角不等式,连接点 a a a 和点 c c c 更优,我们直接删掉点 b b b,连接点 a a a 和点 c c c。否则直接加入点 c c c,连接点 b b b 和点 c c c。
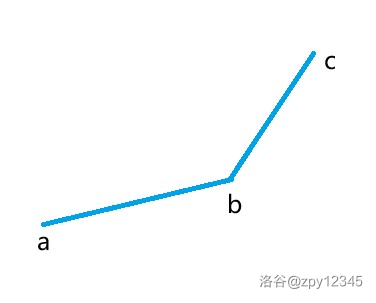
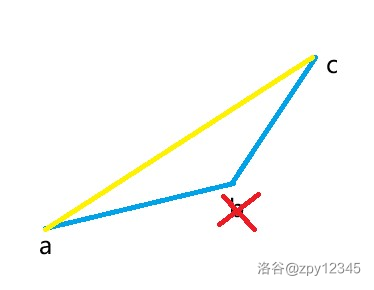
这样就可以求出上凸壳了。
实现过程其实就是单调栈。
其实按照双关键字排序的作用只有求出第一个和最后一个点,在后续算法中,只需要按照横坐标排序即可。同样,我们发现,除了最后一个点之外,其余相同横坐标的情况下,只有纵坐标最高的点有可能成为上凸壳上的点。当然,这里直接用排序好的数组即可,方便,并且相同横坐标下纵坐标低的也不会影响结果。
如何判断是否形成凹多边形?可以发现,直线 a b ab ab 的斜率小于直线 b c bc bc 的斜率,据此判断即可。如果求斜率有精度问题,可以去分母求(详见代码)。
这样,我们就得到了上凸壳的一个性质:其斜率依次递减。
时间复杂度 O(n\\log_{2}{n}) ,瓶颈在于排序。
3.代码
cpp
#include<bits/stdc++.h>
//#define printf __mingw_printf
//在一些本地编译器(如DEV和小熊猫)中,long double有兼容性问题,需要用
//__mingw_printf输出,不过洛谷不需要,而且用__mingw_printf会报错
using namespace std;
const int N=1e5+5;
struct point
{
double x,y;
}a[N],q[N];
int n,tp;
bool cmp(point a,point b)
{
return a.x==b.x?a.y<b.y:a.x<b.x;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lf%lf",&a[i].x,&a[i].y);
sort(a+1,a+1+n,cmp);
q[++tp]=a[1];
for(int i=2;i<=n;i++)//求上凸壳
{
while(tp>=2&&(a[i].y-q[tp].y)*(q[tp].x-q[tp-1].x)>=(q[tp].y-q[tp-1].y)*(a[i].x-q[tp].x))
tp--;
q[++tp]=a[i];
}
long double ans=0;//以防万一爆掉
for(int i=1;i<tp;i++)//计算凸包周长
ans+=sqrt((q[i].y-q[i+1].y)*(q[i].y-q[i+1].y)+(q[i].x-q[i+1].x)*(q[i].x-q[i+1].x));
tp=1,q[tp]=a[n];
for(int i=n-1;i>=1;i--)
{
while(tp>=2&&(a[i].y-q[tp].y)*(q[tp].x-q[tp-1].x)>=(q[tp].y-q[tp-1].y)*(a[i].x-q[tp].x))
tp--;
q[++tp]=a[i];
}
for(int i=1;i<tp;i++)
ans+=sqrt((q[i].y-q[i+1].y)*(q[i].y-q[i+1].y)+(q[i].x-q[i+1].x)*(q[i].x-q[i+1].x));
printf("%.2Lf",ans); //用Lf输出
return 0;
}4.扩展用途
有什么用呢?有没有发现凸包和斜率优化很像?当然还有更多用途,这里就不多说了。