目录
[一、Load Data 加载数据](#一、Load Data 加载数据)
[二、Explore Data 探索数据](#二、Explore Data 探索数据)
[三、OLS analysis 普通最小二乘分析](#三、OLS analysis 普通最小二乘分析)
[1-Day Returns](#1-Day Returns)
[5-Day Returns](#5-Day Returns)
[四、Obtain the residuals 计算残差](#四、Obtain the residuals 计算残差)
[residuals analysis 残差分析](#residuals analysis 残差分析)
[10-Day Returns](#10-Day Returns)
[Monthly Returns](#Monthly Returns)
Statistical inference of stock returns with linear regression
这些需要先从0703中构建数据,然后再这一篇。
一、Load Data 加载数据
python
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
import pandas as pd
from statsmodels.api import OLS, add_constant, graphics
from statsmodels.graphics.tsaplots import plot_acf
from scipy.stats import norm
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_style('whitegrid')
idx = pd.IndexSlice
python
# Load Data
with pd.HDFStore('data.h5') as store:
data = (store['model_data']
.dropna()
.drop(['open', 'close', 'low', 'high'], axis=1))
# Select Investment Universe
data = data[data.dollar_vol_rank<100]
data.info(show_counts=True)输出:
python
<class 'pandas.core.frame.DataFrame'>
MultiIndex: 109434 entries, ('AAL', Timestamp('2013-07-26 00:00:00')) to ('YUM', Timestamp('2015-11-03 00:00:00'))
Data columns (total 65 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 volume 109434 non-null float64
1 dollar_vol 109434 non-null float64
2 dollar_vol_1m 109434 non-null float64
3 dollar_vol_rank 109434 non-null float64
4 rsi 109434 non-null float64
5 bb_high 109434 non-null float64
6 bb_low 109434 non-null float64
7 atr 109434 non-null float64
8 macd 109434 non-null float64
9 return_1d 109434 non-null float64
10 return_5d 109434 non-null float64
11 return_10d 109434 non-null float64
12 return_21d 109434 non-null float64
13 return_42d 109434 non-null float64
14 return_63d 109434 non-null float64
15 return_1d_lag1 109434 non-null float64
16 return_5d_lag1 109434 non-null float64
17 return_10d_lag1 109434 non-null float64
18 return_21d_lag1 109434 non-null float64
19 return_1d_lag2 109434 non-null float64
20 return_5d_lag2 109434 non-null float64
21 return_10d_lag2 109434 non-null float64
22 return_21d_lag2 109434 non-null float64
23 return_1d_lag3 109434 non-null float64
24 return_5d_lag3 109434 non-null float64
25 return_10d_lag3 109434 non-null float64
26 return_21d_lag3 109434 non-null float64
27 return_1d_lag4 109434 non-null float64
28 return_5d_lag4 109434 non-null float64
29 return_10d_lag4 109434 non-null float64
30 return_21d_lag4 109434 non-null float64
31 return_1d_lag5 109434 non-null float64
32 return_5d_lag5 109434 non-null float64
33 return_10d_lag5 109434 non-null float64
34 return_21d_lag5 109434 non-null float64
35 target_1d 109434 non-null float64
36 target_5d 109434 non-null float64
37 target_10d 109434 non-null float64
38 target_21d 109434 non-null float64
39 year_2014 109434 non-null bool
40 year_2015 109434 non-null bool
41 year_2016 109434 non-null bool
42 year_2017 109434 non-null bool
43 month_2 109434 non-null bool
44 month_3 109434 non-null bool
45 month_4 109434 non-null bool
46 month_5 109434 non-null bool
47 month_6 109434 non-null bool
48 month_7 109434 non-null bool
49 month_8 109434 non-null bool
50 month_9 109434 non-null bool
51 month_10 109434 non-null bool
52 month_11 109434 non-null bool
53 month_12 109434 non-null bool
54 capital_goods 109434 non-null bool
55 consumer_durables 109434 non-null bool
56 consumer_non-durables 109434 non-null bool
57 consumer_services 109434 non-null bool
58 energy 109434 non-null bool
59 finance 109434 non-null bool
60 health_care 109434 non-null bool
61 miscellaneous 109434 non-null bool
62 public_utilities 109434 non-null bool
63 technology 109434 non-null bool
64 transportation 109434 non-null bool
dtypes: bool(26), float64(39)
memory usage: 36.5+ MBCreate Model Data
python
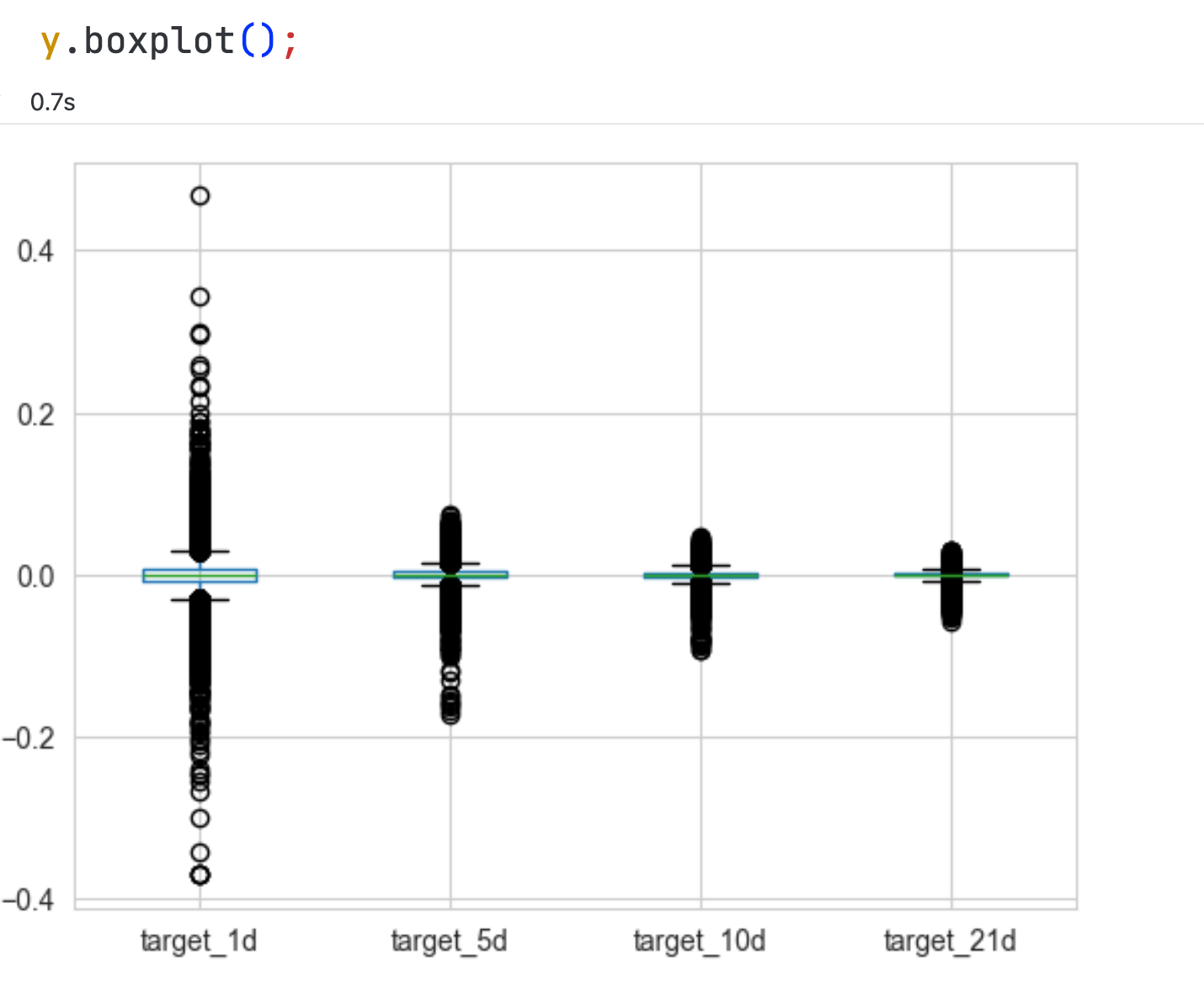
y = data.filter(like='target')
X = data.drop(y.columns, axis=1)
X = X.drop(['dollar_vol', 'dollar_vol_rank', 'volume', 'consumer_durables'], axis=1)如果这里报错的话,要修改上一节0704的代码:
python
prices['sector'] = prices['sector'].str.lower().str.replace(' ', '_') # add code;增加的代码
prices.assign(sector=pd.factorize(prices.sector, sort=True)[0]).to_hdf('data.h5', 'model_data/no_dummies')
prices = pd.get_dummies(prices,
columns=['year', 'month', 'sector'],
prefix=['year', 'month', ''],
prefix_sep=['_', '_', ''],
drop_first=True)
prices.info(show_counts=True)二、Explore Data 探索数据
python
sns.clustermap(y.corr(), cmap=sns.diverging_palette(h_neg=20, h_pos=220), center=0, annot=True, fmt='.2%');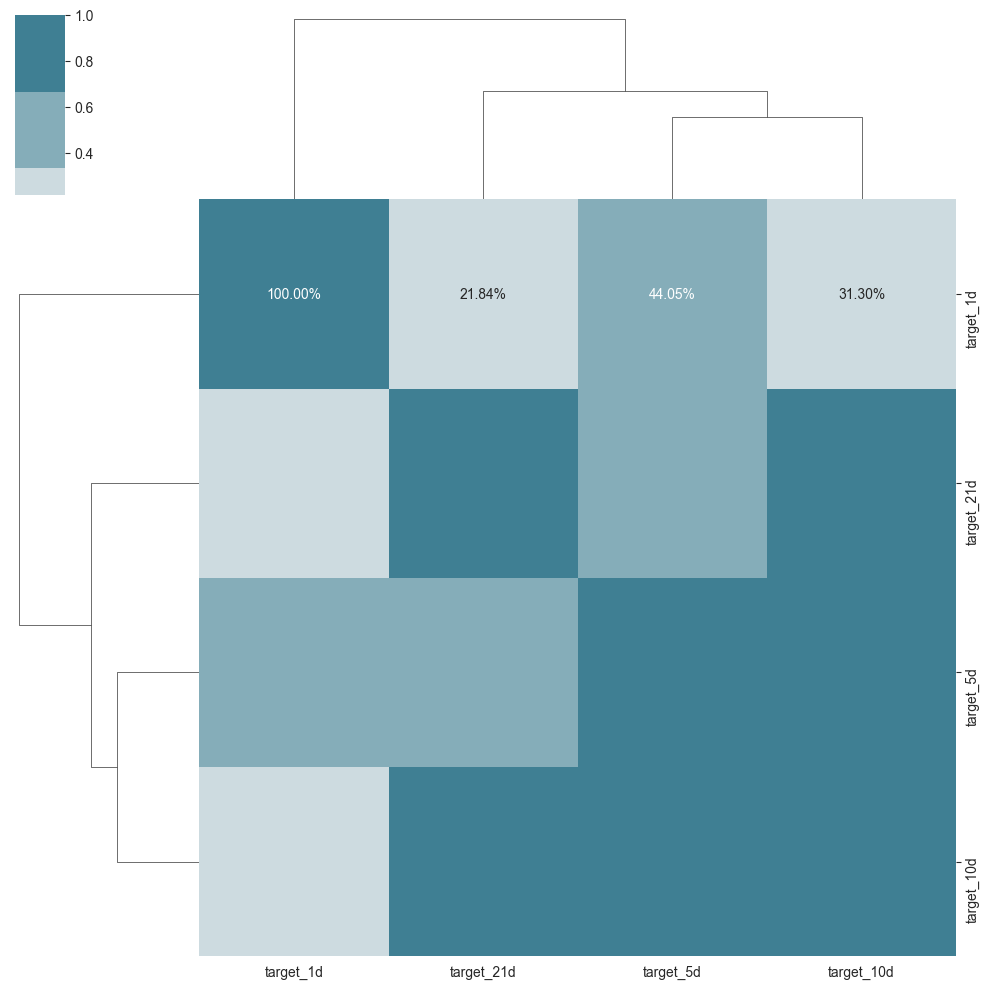
python
sns.clustermap(X.corr(), cmap=sns.diverging_palette(h_neg=20, h_pos=220), center=0);
plt.gcf().set_size_inches((14, 14))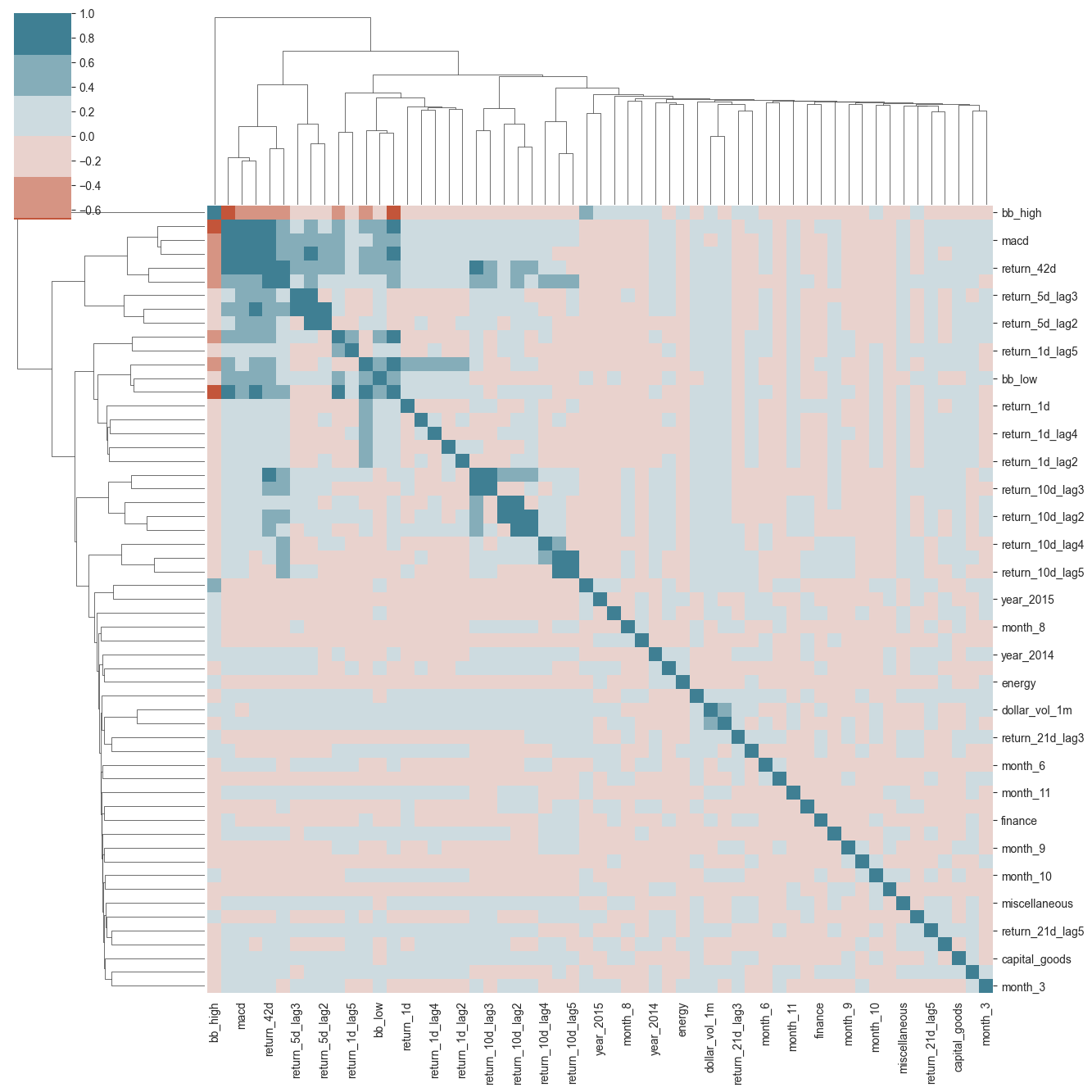
热力图结论:
热力图显示了特征之间的相关性。
相关系数的范围在-1到1之间,值越接近1或-1,说明特征之间的相关性越强。
相关系数为0说明特征之间没有相关性。
Conclusion of heat map:
The heatmap shows the correlation between features.
The range of the correlation coefficient is between -1 and 1. The closer the value is to 1 or -1, the stronger the correlation between the features.
A correlation coefficient of 0 indicates that there is no correlation between the features.
python
corr_mat = X.corr().stack().reset_index()
corr_mat.columns=['var1', 'var2', 'corr']
corr_mat = corr_mat[corr_mat.var1!=corr_mat.var2].sort_values(by='corr', ascending=False)
# corr_mat.head().append(corr_mat.tail()) old code is bad; 作者原始代码已经不行了
pd.concat([corr_mat.head(), corr_mat.tail()]) # pandas ≥ 2.0 good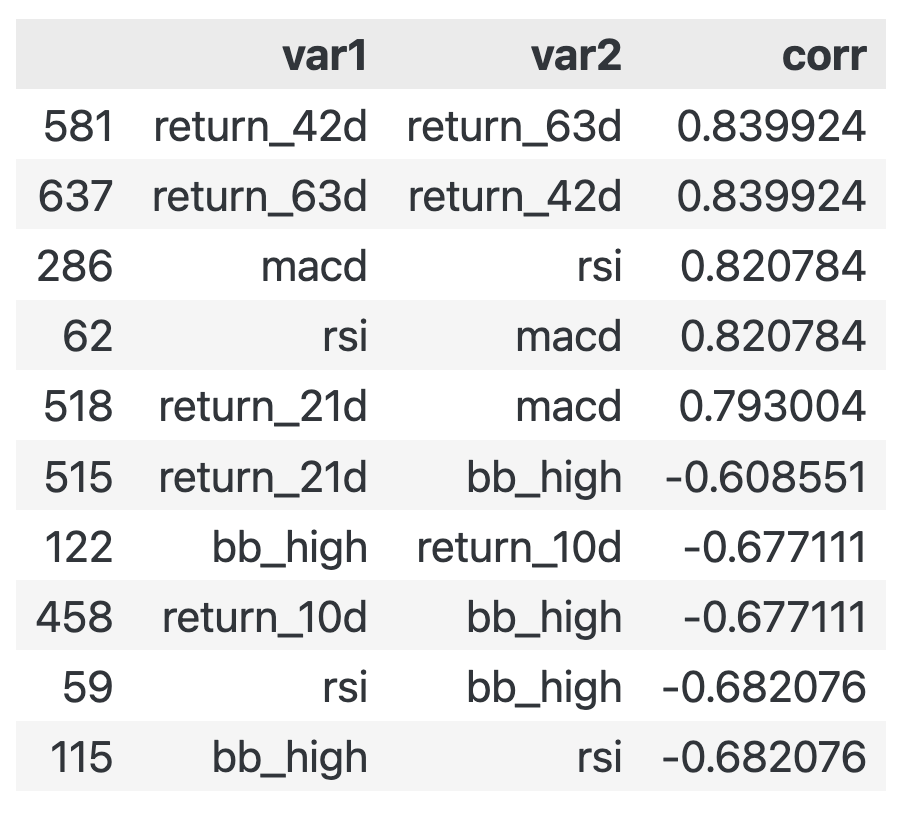
三、OLS analysis 普通最小二乘分析
Linear Regression for Statistical Inference: OLS with statsmodels
用statsmodels库进行线性回归分析,OLS线性回归
Ticker-wise standardization
statsmodels warns of high design matrix condition numbers. This can arise when the variables are not standardized and the Eigenvalues differ due to scaling. The following step avoids this warning.
python
sectors = X.iloc[:, -10:]
X = (X.drop(sectors.columns, axis=1)
.groupby(level='ticker')
.transform(lambda x: (x - x.mean()) / x.std())
.join(sectors)
.fillna(0))1-Day Returns
python
target = 'target_1d'
# this is MultiIndex
# model = OLS(endog=y[target], exog=add_constant(X)) # old code is bad; 老代码失效
X = X.astype(float)
model = OLS(endog=y[target], exog=add_constant(X)) # this is good.
trained_model = model.fit()
print(trained_model.summary())
# R-squared is only 0.009, less than 0.5; bad输出:
(R方值比较小的,低于0.5,说明拟合不好)
python
OLS Regression Results
==============================================================================
Dep. Variable: target_1d R-squared: 0.009
Model: OLS Adj. R-squared: 0.009
Method: Least Squares F-statistic: 18.36
Date: Sun, 28 Sep 2025 Prob (F-statistic): 5.52e-181
Time: 14:20:47 Log-Likelihood: 2.8809e+05
No. Observations: 109434 AIC: -5.761e+05
Df Residuals: 109376 BIC: -5.755e+05
Df Model: 57
Covariance Type: nonrobust
=========================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------------
const 8.573e-05 0.000 0.543 0.587 -0.000 0.000
dollar_vol_1m -0.0004 6.78e-05 -5.392 0.000 -0.000 -0.000
rsi 0.0001 0.000 0.758 0.449 -0.000 0.001
bb_high 0.0002 0.000 0.759 0.448 -0.000 0.001
bb_low 0.0006 0.000 2.717 0.007 0.000 0.001
atr 2.421e-06 7.35e-05 0.033 0.974 -0.000 0.000
macd -0.0004 0.000 -1.764 0.078 -0.001 4.68e-05
return_1d 0.0024 0.000 8.693 0.000 0.002 0.003
return_5d -0.0010 0.001 -1.151 0.250 -0.003 0.001
return_10d -0.0061 0.001 -6.641 0.000 -0.008 -0.004
return_21d 0.0024 0.000 5.552 0.000 0.002 0.003
return_42d -0.0035 0.001 -6.605 0.000 -0.005 -0.002
return_63d -0.0015 0.000 -3.711 0.000 -0.002 -0.001
return_1d_lag1 0.0022 0.000 7.945 0.000 0.002 0.003
return_5d_lag1 0.0047 0.001 7.420 0.000 0.003 0.006
return_10d_lag1 -0.0007 0.001 -0.639 0.523 -0.003 0.001
return_21d_lag1 0.0025 0.000 6.952 0.000 0.002 0.003
return_1d_lag2 0.0023 0.000 8.058 0.000 0.002 0.003
return_5d_lag2 0.0007 0.001 1.022 0.307 -0.001 0.002
return_10d_lag2 -0.0002 0.001 -0.193 0.847 -0.002 0.001
return_21d_lag2 -6.892e-05 0.000 -0.250 0.802 -0.001 0.000
return_1d_lag3 0.0022 0.000 7.804 0.000 0.002 0.003
return_5d_lag3 0.0013 0.001 1.807 0.071 -0.000 0.003
return_10d_lag3 0.0006 0.000 4.431 0.000 0.000 0.001
return_21d_lag3 -0.0003 5.57e-05 -4.564 0.000 -0.000 -0.000
return_1d_lag4 0.0025 0.000 8.871 0.000 0.002 0.003
return_5d_lag4 0.0009 0.001 1.511 0.131 -0.000 0.002
return_10d_lag4 0.0005 0.000 4.674 0.000 0.000 0.001
return_21d_lag4 -8.646e-07 5.51e-05 -0.016 0.987 -0.000 0.000
return_1d_lag5 -9.493e-05 6.16e-05 -1.540 0.123 -0.000 2.59e-05
return_5d_lag5 0.0004 0.001 0.692 0.489 -0.001 0.001
return_10d_lag5 0.0008 9.86e-05 7.792 0.000 0.001 0.001
return_21d_lag5 0.0001 5.48e-05 2.023 0.043 3.44e-06 0.000
year_2014 -0.0003 8.28e-05 -4.111 0.000 -0.001 -0.000
year_2015 -0.0006 9.04e-05 -7.115 0.000 -0.001 -0.000
year_2016 -0.0004 8.84e-05 -5.039 0.000 -0.001 -0.000
year_2017 -0.0002 8.81e-05 -2.175 0.030 -0.000 -1.89e-05
month_2 0.0010 7.23e-05 14.348 0.000 0.001 0.001
month_3 0.0004 7.44e-05 4.885 0.000 0.000 0.001
month_4 0.0005 7.29e-05 6.433 0.000 0.000 0.001
month_5 0.0005 7.22e-05 6.911 0.000 0.000 0.001
month_6 0.0004 7.34e-05 5.687 0.000 0.000 0.001
month_7 0.0007 7.6e-05 8.693 0.000 0.001 0.001
month_8 4.93e-05 7.66e-05 0.644 0.520 -0.000 0.000
month_9 0.0004 7.53e-05 4.810 0.000 0.000 0.001
month_10 0.0006 7.77e-05 8.279 0.000 0.000 0.001
month_11 0.0006 7.57e-05 7.491 0.000 0.000 0.001
month_12 0.0004 7.38e-05 5.094 0.000 0.000 0.001
capital_goods 0.0006 0.000 2.428 0.015 0.000 0.001
consumer_non-durables 0.0004 0.000 1.469 0.142 -0.000 0.001
consumer_services 0.0004 0.000 2.130 0.033 3.6e-05 0.001
energy 0.0001 0.000 0.495 0.621 -0.000 0.001
finance 0.0006 0.000 2.573 0.010 0.000 0.001
health_care 0.0003 0.000 1.733 0.083 -4.55e-05 0.001
miscellaneous 0.0009 0.000 2.445 0.014 0.000 0.002
public_utilities 5.961e-06 0.000 0.018 0.986 -0.001 0.001
technology 0.0008 0.000 3.945 0.000 0.000 0.001
transportation 0.0006 0.000 1.825 0.068 -4.21e-05 0.001
==============================================================================
Omnibus: 32445.335 Durbin-Watson: 2.012
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4401670.731
Skew: -0.255 Prob(JB): 0.00
Kurtosis: 34.066 Cond. No. 77.0
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.5-Day Returns
python
target = 'target_5d'
model = OLS(endog=y[target], exog=add_constant(X))
trained_model = model.fit()
print(trained_model.summary())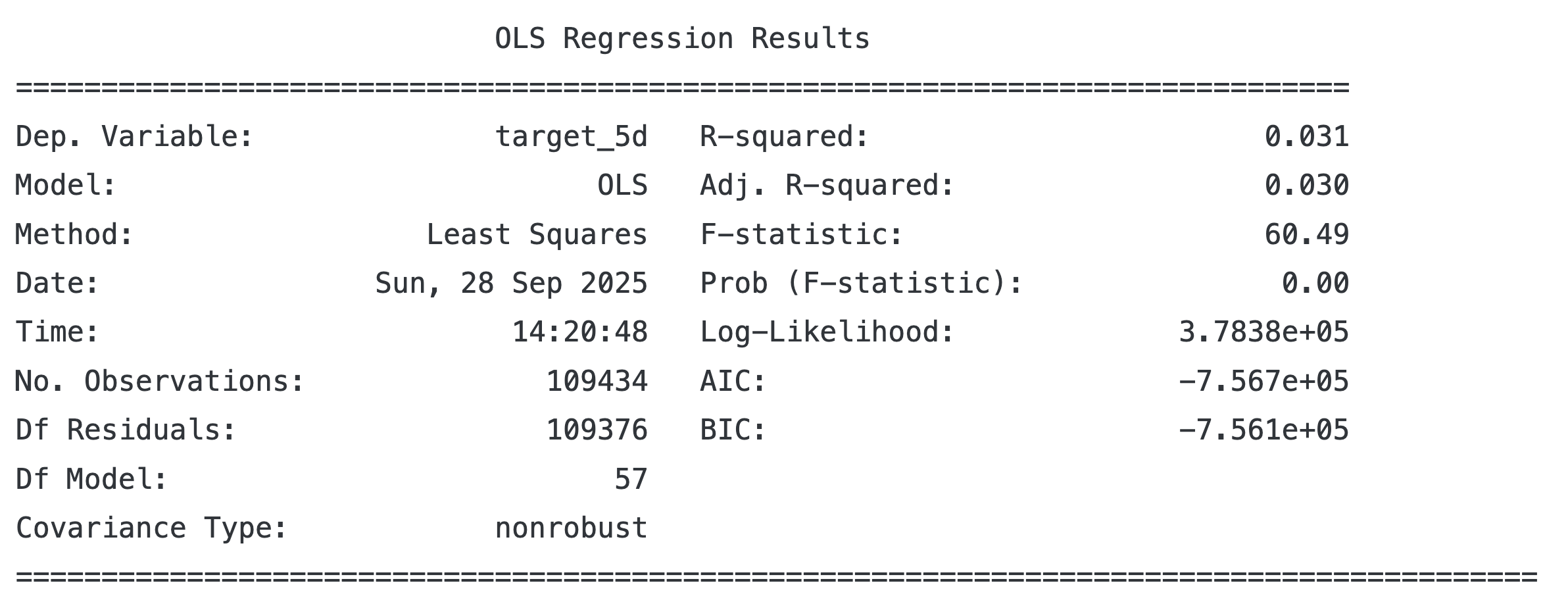
R方值比1-Day Returns要高一点
四、Obtain the residuals 计算残差
residuals analysis 残差分析
python
preds = trained_model.predict(add_constant(X))
residuals = y[target] - preds
fig, axes = plt.subplots(ncols=2, figsize=(14,4))
sns.distplot(residuals, fit=norm, ax=axes[0], axlabel='Residuals', label='Residuals')
axes[0].set_title('Residual Distribution')
axes[0].legend()
plot_acf(residuals, lags=10, zero=False, ax=axes[1], title='Residual Autocorrelation')
axes[1].set_xlabel('Lags')
sns.despine()
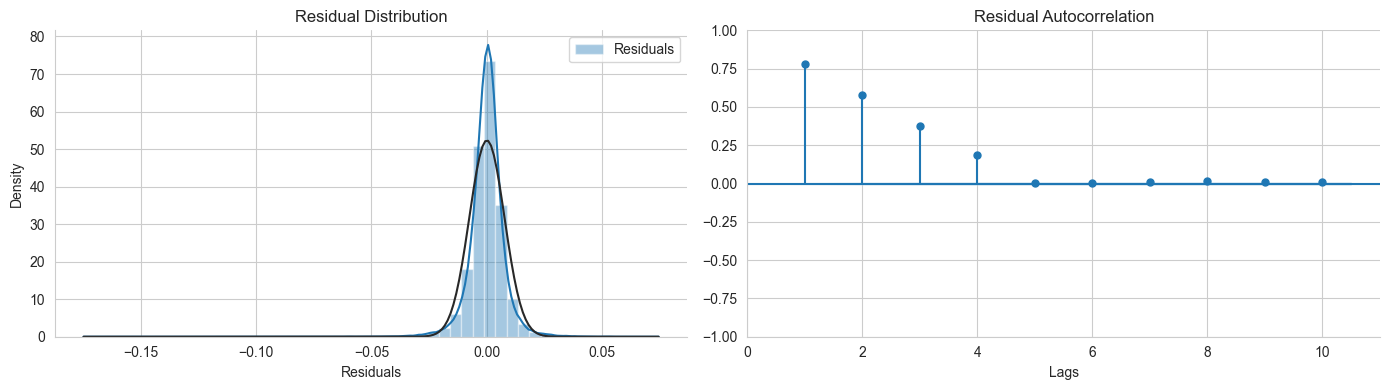
fig.tight_layout();The residuals are normally distributed, it's good.
残差的分布是正态分布,这是好的。
But the autocorrelation is not good.
残差的自相关图不是很好(前几个Lags自相关系数在0.2以上),说明残差之间不是独立的。
10-Day Returns
python
target = 'target_10d'
model = OLS(endog=y[target], exog=add_constant(X))
trained_model = model.fit()
print(trained_model.summary())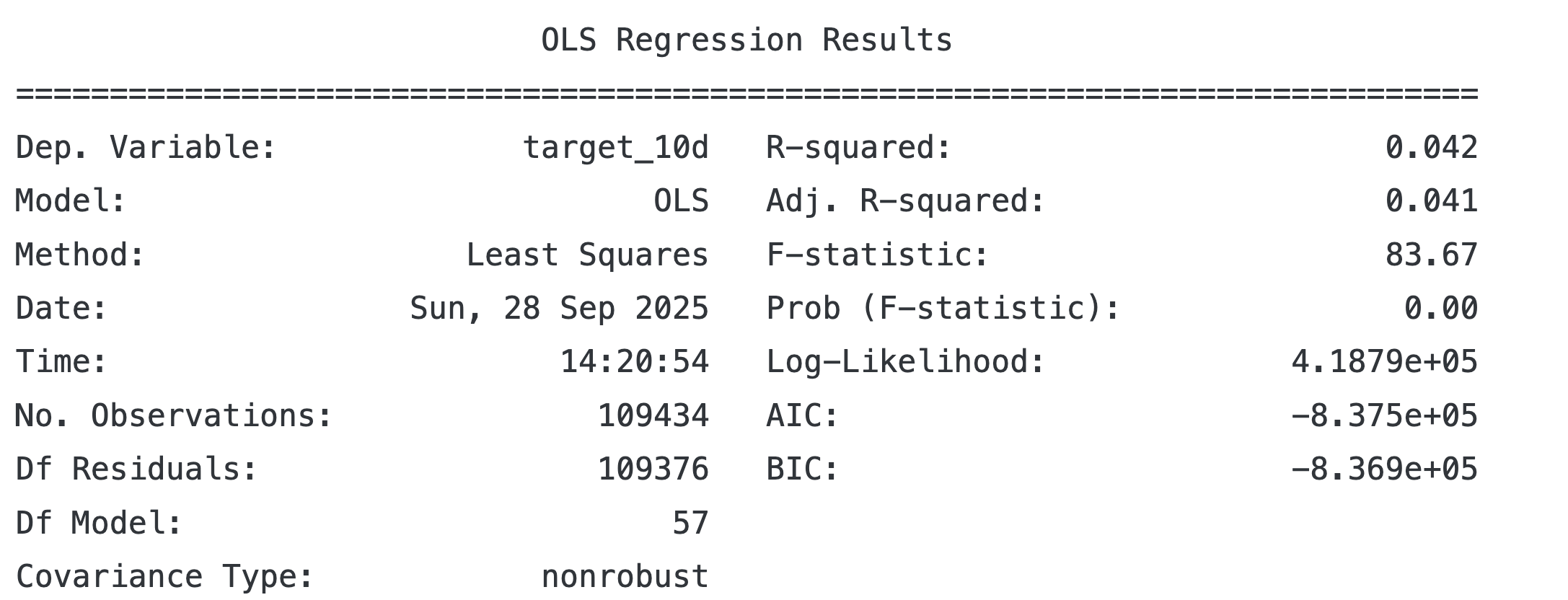
Monthly Returns
python
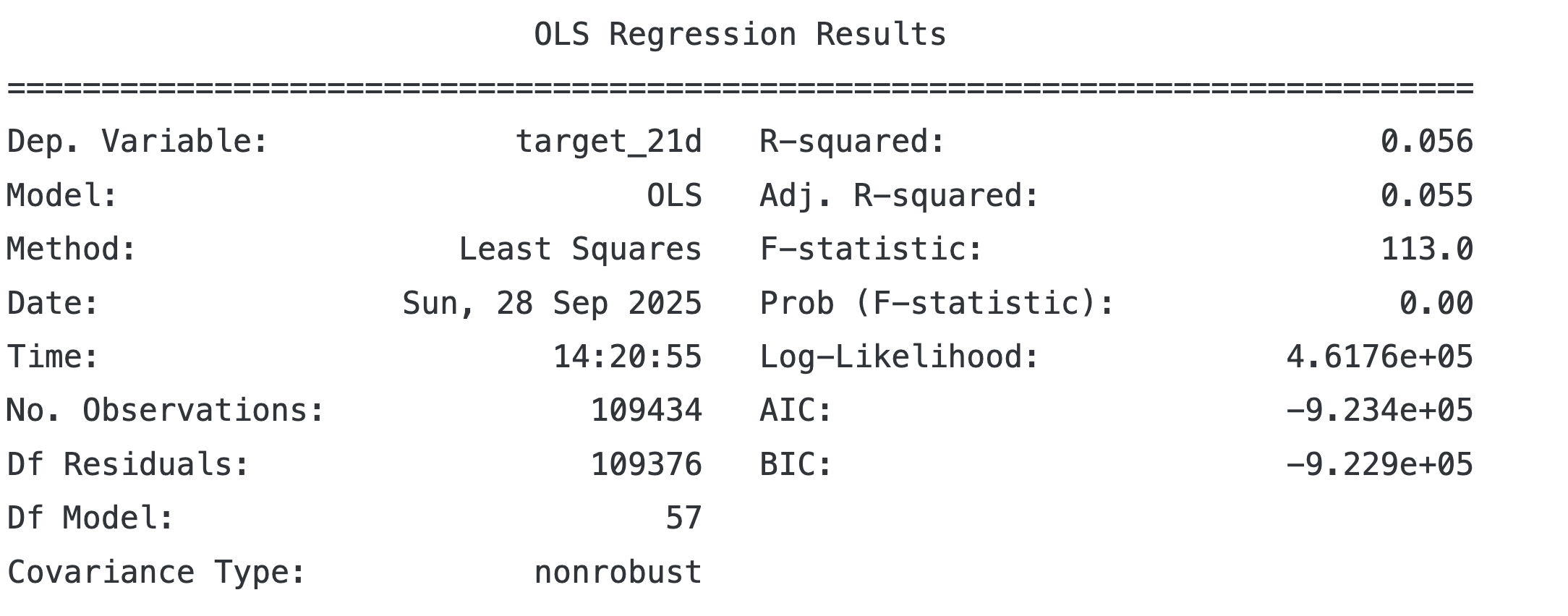
target = 'target_21d'
model = OLS(endog=y[target], exog=add_constant(X))
trained_model = model.fit()
print(trained_model.summary())