力扣 15.三数之和（medium）（双指针）

解法一：排序后暴力枚举然后利用set去重

答案中不可以包含重复的三元组，输出的顺序和三元组的顺序并不重要。根据这两点要求我们需要对数组进行排序，排序后三层for循环嵌套遍历数组可以找出所有满足（i != j、i != k 且 j != k ，同时还满足 nums $i$ + nums $j$ + nums $k$ == 0）的三元组，而在这些三元组中，重复的三元组因为数组有序而完全一样（包括顺序）然后把全部的三元组一股脑扔给set容器，set会帮我们完成去重，最后输出结果。时间复杂度O(n^3) (该解法只解释思路，不做具体演示，我们主要学习下面这种解法)

解法二：排序+双指针

算法思路：

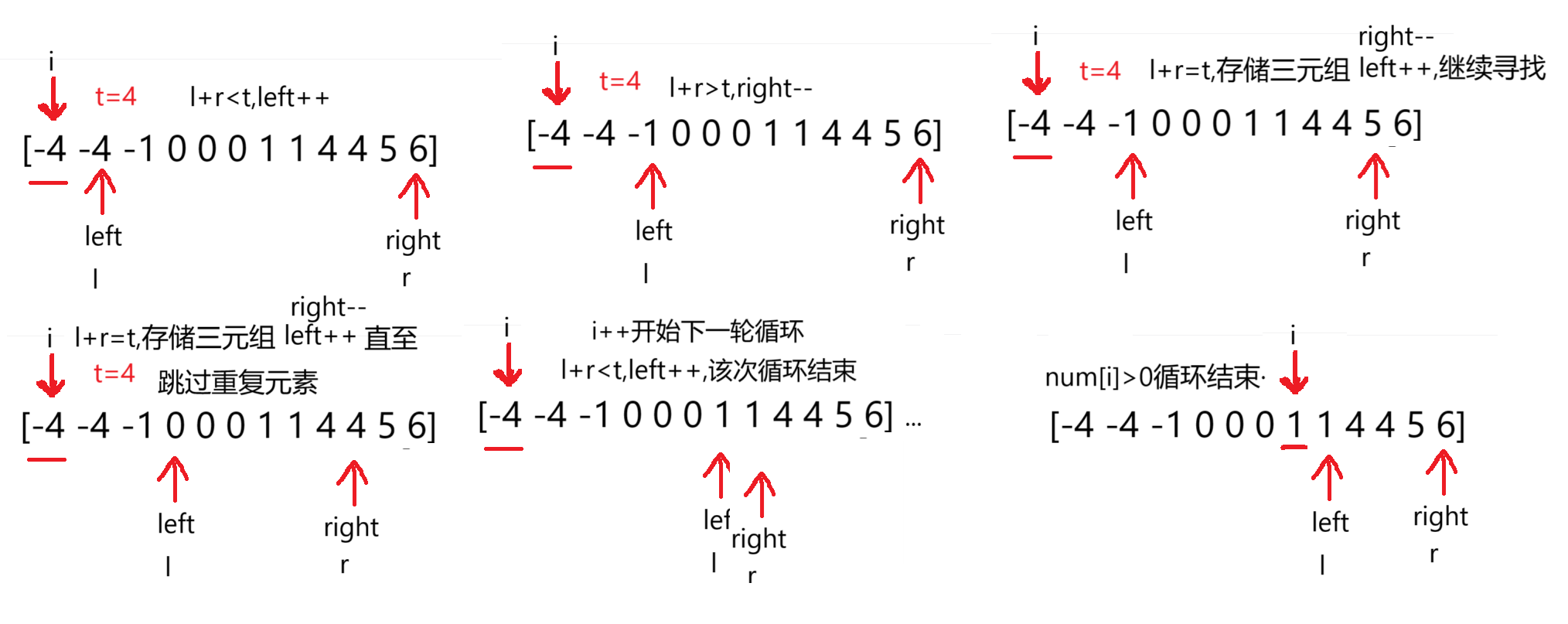
1.先对数组排序，令其变为有序，固定左侧i,定义t=-num $i$ ,定义left，right指针，l，r分别是其所指向的值，在 $left,right$ 区间中遍历使l+r=t

2.若l+r>t,right--,若l+r<t,left++,若l+r=t，存储三元组target,left++,ight--。l,r循环直至left>=right

3.然后i++，开始下一轮循环直至i=n(一个小优化：当num $i$ >0时就可以结束循环了，之后不可能有符合条件的三元组)

处理细节问题：

1.去重

当找到符合条件的三元组时，left，right要跳过重复元素s

当使用完一次双指针算法后，i也要跳过重复元素

2.不漏

找到一种结果后不要停，缩小区间继续寻找

3.避免越界（特殊情况）

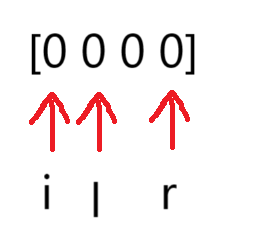
每次跳过重复元素时都要判断是否越界

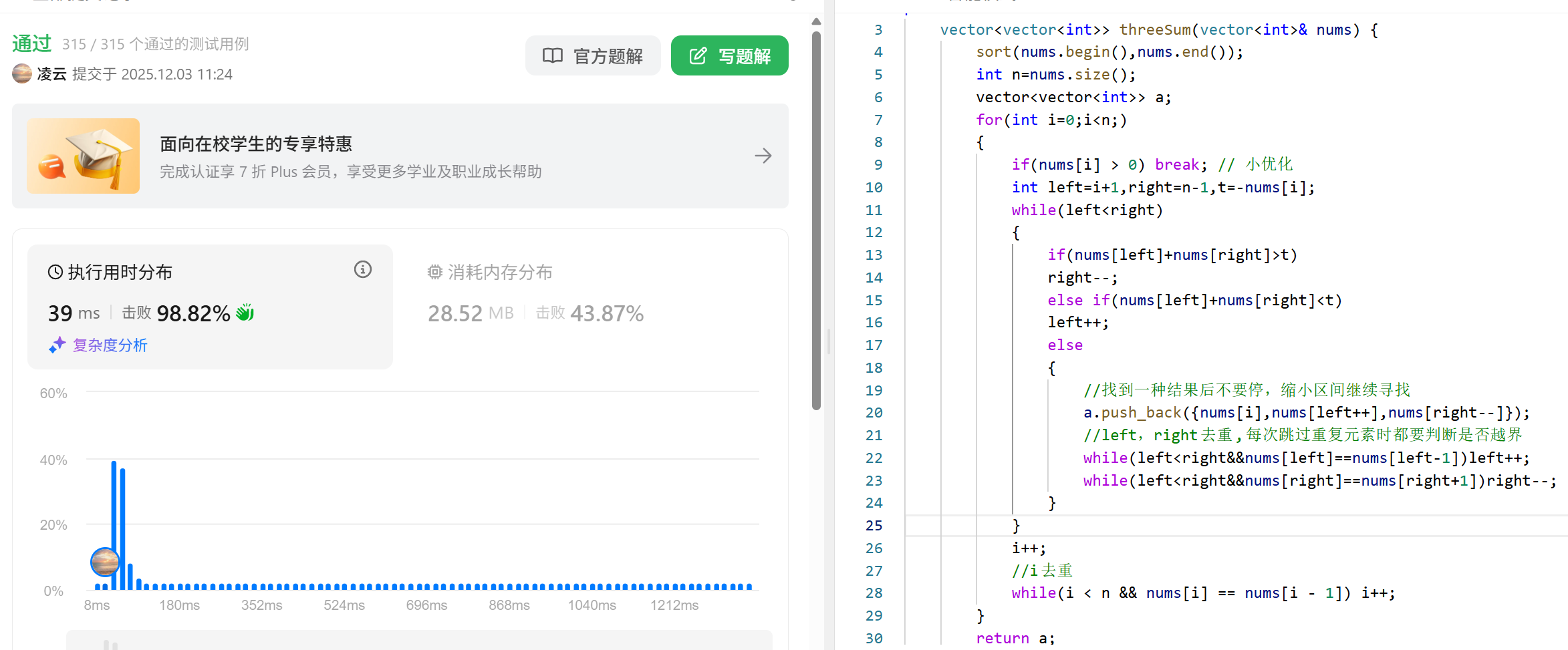
代码:

cpp 复制代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int n=nums.size();
        vector<vector<int>> a;
        for(int i=0;i<n;)
        {
            if(nums[i] > 0) break; // 小优化
            int left=i+1,right=n-1,t=-nums[i];
            while(left<right)
            {
                if(nums[left]+nums[right]>t)
                right--;
                else if(nums[left]+nums[right]<t)
                left++;
                else
                {
                    //找到一种结果后不要停，缩小区间继续寻找
                    a.push_back({nums[i],nums[left++],nums[right--]});
                    //left，right去重,每次跳过重复元素时都要判断是否越界
                    while(left<right&&nums[left]==nums[left-1])left++;
                    while(left<right&&nums[right]==nums[right+1])right--;
                }
            }
            i++;
            //i去重
            while(i < n && nums[i] == nums[i - 1]) i++;
        }
        return a;
    }
};