稀疏且难以察觉的对抗攻击

原文链接:https://arxiv.org/pdf/1909.05040v1
摘要
神经网络已被证明容易受到各种对抗攻击。从安全角度来看,高度稀疏的对抗攻击尤其危险。另一方面,稀疏攻击的逐像素扰动通常很大,因此可能被检测到。我们提出了一种新的黑盒技术来生成对抗样本,旨在最小化与原始图像的 l 0 l_{0} l0-距离。大量实验表明,我们的攻击优于或可与现有技术相媲美。此外,我们可以集成对分量扰动的附加约束。允许像素仅在高变化区域改变并避免沿轴对齐边缘进行更改,使得我们的对抗样本几乎难以察觉。此外,我们使投影梯度下降攻击适应 l 0 l_{0} l0-范数,并集成了分量约束。这使我们能够进行对抗训练,以增强分类器对稀疏且难以察觉的对抗操作的鲁棒性。
1 引言
最先进的神经网络并不鲁棒 [3, 30, 12],因为正确分类的输入的非常小的对抗性变化会导致错误的决策。虽然 [30, 12] 在目标识别任务中提出了这个问题,但这个问题本身在电子邮件垃圾邮件分类领域已经讨论了一段时间 [9, 19]。神经网络的这种非鲁棒行为在安全关键系统(例如自动驾驶或医疗诊断系统)中使用此类分类器进行决策时是一个问题。因此,意识到可能的漏洞非常重要,因为它们可能导致超出紧迫安全问题之外的致命故障 [18]。
最近的攻击研究可以分为白盒攻击 [23, 6, 5, 21, 8](在攻击时可以访问模型)和黑盒攻击 [7, 4, 13, 2](只能查询分类器的输出或所有类的置信度分数)。通常,攻击试图找到决策边界上或附近点,其中距离在像素空间中测量,最常用的是关于 l ∞ l_{\infty} l∞-和 l 2 l_{2} l2-范数 [23, 6, 5, 8],或者试图在某些原始图像的 ϵ \epsilon ϵ-球内最大化损失或最小化正确类的置信度 [21]。利用几何变换的非逐像素攻击已在 [14, 32] 中提出。虽然有人认为对抗性变化不会在实际场景中发生,但这一论点在 [16, 11] 中被驳斥。训练期间的对抗攻击早期被提出作为一种潜在的防御手段 [30, 12],现在称为对抗训练。以 [21] 中提出的形式,这是少数不易被攻破的防御手段之一 [5, 1]。
在本文中,我们专门处理稀疏对
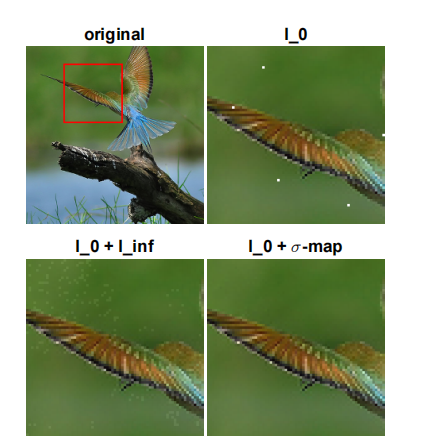
图 1:左上:带缩放框的原始图像,右上:我们的 l 0 l_{0} l0-攻击,只有非常少的像素(仅 0.04 % 0.04\% 0.04%)被改变,但修改后的像素清晰可见,左下:[22] 中提出的 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击的结果,修改是稀疏的( 2.7 % 2.7\% 2.7% 的像素被改变),但清晰可见,右下:我们的稀疏( 2.7 % 2.7\% 2.7% 的像素被改变)但难以察觉的攻击( l 0 + σ l_{0}+\sigma l0+σ-map)。
抗性攻击,即我们希望修改最少数量的像素以改变决策。目前有基于集成 l 0 l_{0} l0-约束的梯度方法变体的白盒攻击 [6, 22],或者主要是使用局部搜索或进化算法的黑盒攻击 [24, 29, 28]。本文有以下方法论贡献:1)我们提出了一种基于局部搜索的新型黑盒攻击,其性能优于所有现有的 l 0 l_{0} l0-攻击;2)我们提出了用于投影到 l 0 l_{0} l0-球(或 l 0 l_{0} l0-球与分量约束的交集)的闭式表达式或简单算法,以便将 [21] 的 PGD 攻击扩展到所考虑的场景;3)由于稀疏攻击通常清晰可见,因此至少在某些情况下易于检测(见图 1 右上图),我们将稀疏性约束( l 0 l_{0} l0-球)与分量约束结合起来,并扩展了上述两种 l 0 l_{0} l0-攻击以产生稀疏且难以察觉的对抗扰动。
与引入全局分量约束的 [22] 相比(见图 1 左下图),我们建议使用局部自适应的分量约束。这些局部约束确保更改通常不可见,也就是说,我们既不会过多地改变颜色,也不会沿着坐标轴对齐的边缘(可视化见附录)或在颜色均匀的区域(见图 1 右下图)改变像素。这与 [20] 一致并显著改进,[20] 建议在高度方差的区域扰动像素以产生不易识别的修改。事实上,经常使用的 l ∞ l_{\infty} l∞-攻击只轻微修改每个像素但必须操纵所有像素,似乎并不能模拟实际可能发生的扰动。我们认为我们的稀疏且难以察觉的攻击可能在实际中发生,并且对应于即使在非常小的尺度上也不会改变图像语义的修改。我们论文的好消息是,此类攻击的成功率(标准模型为 50-70%)低于常用攻击的成功率------尽管如此,我们发现这种操纵竟然是可能的,这令人不安。因此,我们还测试了对抗训练是否可以降低此类攻击的成功率。我们发现,关于 l 2 l_{2} l2 的对抗训练部分降低了 l 0 l_{0} l0-攻击的有效性,而关于 l 2 l_{2} l2 或 l ∞ l_{\infty} l∞ 的对抗训练有助于提高对稀疏且难以察觉攻击的鲁棒性。最后,我们引入了专门针对我们的两种攻击模型的鲁棒性的对抗训练。
2 稀疏且难以察觉的对抗攻击
令 f : R d ⟶ R K f:\mathbb{R}^{d}\longrightarrow\mathbb{R}^{K} f:Rd⟶RK 为一个多类分类器,其中 d d d 是输入维度, K K K 是类别数。测试点 x ∈ R d x\in\mathbb{R}^{d} x∈Rd 被分类为 c = arg max r = 1 , ... , K f r ( x ) c=\operatorname*{arg\,max}{r=1,\ldots,K}f{r}(x) c=argmaxr=1,...,Kfr(x)。 x ∈ R d x\in\mathbb{R}^{d} x∈Rd 关于距离函数 γ : R d ⟶ R + \gamma:\mathbb{R}^{d}\longrightarrow\mathbb{R}_{+} γ:Rd⟶R+ 的最小对抗扰动 y ∗ y^{*} y∗ 是优化问题的解 y ∗ ∈ R d y^{*}\in\mathbb{R}^{d} y∗∈Rd
min y ∈ R d γ ( y − x ) \min_{y\in\mathbb{R}^{d}} \gamma(y-x) y∈Rdminγ(y−x) 满足 arg max r = 1 , ... , K f r ( y ) ≠ arg max r = 1 , ... , K f r ( x ) , \operatorname*{arg\,max}{r=1,\ldots,K}f{r}(y)\neq\operatorname* {arg\,max}{r=1,\ldots,K}f{r}(x), r=1,...,Kargmaxfr(y)=r=1,...,Kargmaxfr(x), (1) y ∈ C , y\in C, y∈C,
其中 C C C 是有效输入需要满足的约束集合(例如,图像被缩放至 [ 0 , 1 ] d [0,1]^{d} [0,1]d 内)。换句话说: y ∗ y^{*} y∗ 是距离 x x x 最近的点(关于距离函数 γ \gamma γ),其分类结果与 x x x 不同。
稀疏 l 0 l_{0} l0-攻击
在 l 0 l_{0} l0-攻击中,人们感兴趣的是找到改变决策所需改变的最少像素数。我们在下文中将具有 d d d 个像素的灰度图像 x x x 表示为 [ 0 , 1 ] d [0,1]^{d} [0,1]d 中的向量,将具有 d d d 个像素的彩色图像 x x x 表示为 [ 0 , 1 ] d × 3 [0,1]^{d\times 3} [0,1]d×3 中的矩阵 x x x, x i x_{i} xi 表示第 i i i 个像素及其 RGB 三个颜色通道。相应的距离函数 γ \gamma γ 因此对于灰度图像给出为标准 l 0 l_{0} l0-范数
γ ( y − x ) = ∑ i = 1 d 1 { ∣ y i − x i ∣ ≠ 0 } \gamma(y-x) = \sum_{i=1}^{d} \mathbb{1}_{\{|y_i - x_i| \neq 0\}} γ(y−x)=i=1∑d1{∣yi−xi∣=0}
对于彩色图像为
γ ( y − x ) = ∑ i = 1 d max j = 1 , ... , 3 1 ∣ y i j − x i j ∣ ≠ 0 , \gamma(y-x)=\sum_{i=1}^{d}\max_{j=1,\ldots,3}\mathbb{1}{|y{ij}-x_{ij}|\neq 0}, γ(y−x)=i=1∑dj=1,...,3max1∣yij−xij∣=0, (3)
其中内部最大化检查像素 i i i 的任何颜色通道 j j j 是否被更改。从实际的角度来看, l 0 l_{0} l0-攻击基本上测试了模型对于像素故障或物体上的大型局部变化(例如冰箱上的贴纸或挡风玻璃上的灰尘/污垢)的脆弱程度。
稀疏且难以察觉的攻击
l 0 l_{0} l0-攻击的问题在于它们改变每个像素的方式完全不受约束。因此,被扰动的像素通常具有与周围像素完全不同的颜色,因此很容易被看到。另一方面,使用距离函数的 l ∞ l_{\infty} l∞-攻击
γ ( y − x ) = max i = 1 , ... , d max j = 1 , ... , 3 ∣ y i j − x i j ∣ , \gamma(y-x)=\max_{i=1,\ldots,d}\max_{j=1,\ldots,3}|y_{ij}-x_{ij}|, γ(y−x)=i=1,...,dmaxj=1,...,3max∣yij−xij∣,
已知会导致每个像素的非常小的变化,但必须修改每个像素和颜色通道。从实际角度来看,这似乎是一个相当不现实的扰动模型。一个在实际场景中更可能发生的攻击模型是当变化是
稀疏但也难以察觉时。为了实现这一点,我们提出了对允许的通道变化的附加约束。在 [22] 中,他们建议对于某个固定的 δ > 0 \delta>0 δ>0,采用以下形式的全局界限
x i j − δ ≤ y i j ≤ x i j + δ , x_{ij}-\delta\leq y_{ij}\leq x_{ij}+\delta, xij−δ≤yij≤xij+δ,
这应确保更改不可见(我们在下文中将具有 l 0 l_{0} l0-范数和这些全局分量界限的攻击称为 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击)。然而,这些全局界限完全与图像无关,因此 δ \delta δ 必须非常小,以便即使在均匀颜色区域(例如天空,几乎任何变化都很容易被发现)中更改也不可见。我们建议采用考虑图像结构的图像特定局部界限。我们有两个具体目标:
- 我们不希望沿着与坐标轴对齐的边缘进行更改,因为这些更改很容易被发现和检测到。
- 我们不想改变颜色太多,而是只调整其强度并大致保持其饱和度水平。
为了实现这一点,我们计算每个颜色通道在 x x x 轴和 y y y 轴方向上与两个紧邻像素和原始像素的标准差。我们将相应的值表示为 σ i j ( x ) \sigma^{(x)}{ij} σij(x) 和 σ i j ( y ) \sigma^{(y)}{ij} σij(y),并定义 σ i j = min { σ i j ( x ) , σ i j ( y ) } \sigma_{ij}=\sqrt{\min\{\sigma^{(x)}{ij},\sigma^{(y)}{ij}\}} σij=min{σij(x),σij(y)} 。由于 σ i j ( x ) , σ i j ( y ) ∈ [ 0 , 1 ] \sigma^{(x)}{ij},\sigma^{(y)}{ij}\in[0,1] σij(x),σij(y)∈[0,1],平方根会相对显著地增加较小的 min { σ i j ( x ) , σ i j ( y ) } \min\{\sigma^{(x)}{ij},\sigma^{(y)}{ij}\} min{σij(x),σij(y)} 值。通过这种方式,我们既扩大了可能的对抗样本的空间,又防止了在零方差区域进行扰动。实际上,我们只允许更改后的图像 y y y 具有由下式给出的值
y i j = ( 1 + λ i σ i j ) x i j , 其中 − κ ≤ λ i ≤ κ , y_{ij}=(1+\lambda_{i}\sigma_{ij})x_{ij},\ \text{ 其中 } -\kappa\leq\lambda_{i} \leq\kappa, yij=(1+λiσij)xij, 其中 −κ≤λi≤κ, (4)
其中 κ > 0 \kappa>0 κ>0。此外,我们强制执行框约束 y ∈ [ 0 , 1 ] d × 3 y\in[0,1]^{d\times 3} y∈[0,1]d×3。注意,参数 λ i \lambda_{i} λi 对应于像素 i i i 的强度变化,最大为 ± κ ∑ j = 1 3 σ i j x i j \pm \kappa\sum_{j=1}^{3}\sigma_{ij}x_{ij} ±κ∑j=13σijxij,因为
∑ j = 1 3 y i j = ∑ j = 1 3 x i j + λ i ∑ j = 1 3 σ i j x i j . \sum_{j=1}^{3}y_{ij}=\sum_{j=1}^{3}x_{ij}+\lambda_{i}\sum_{j=1}^{3}\sigma_{ij}x_ {ij}. j=1∑3yij=j=1∑3xij+λij=1∑3σijxij.
因此,我们只是改变像素的强度而不是实际的颜色。此外,请注意,如果 σ i j \sigma_{ij} σij 对于 j = 1 , ... , 3 j=1,\ldots,3 j=1,...,3 是相等的,则这种变化也保持了颜色值的饱和度¹。因此我们满足了上面的第二个要求。此外,第一个要求也得到了满足,因为 σ i j = min { σ i j ( x ) , σ i j ( y ) } \sigma_{ij}=\sqrt{\min\{\sigma^{(x)}{ij},\sigma^{(y)}{ij}\}} σij=min{σij(x),σij(y)} ,这意味着如果沿着一个坐标在所有颜色通道中没有变化,则该像素根本无法修改。因此,沿着坐标对齐的边缘显示颜色没有变化的像素将不会被更改。稀疏且难以察觉攻击的攻击模型将缩写为 l 0 + σ l_{0}+\sigma l0+σ-map。对于灰度图像 x ∈ [ 0 , 1 ] d x\in[0,1]^{d} x∈[0,1]d,我们改用
脚注1:在 HSV 颜色空间中,颜色的饱和度定义为 1 − min { R , G , B } 1-\min\{R,G,B\} 1−min{R,G,B},其中 R , G , B R,G,B R,G,B 是 RGB 颜色空间中的红/绿/蓝颜色通道。
y i = x i + λ i σ i , 其中 − κ ≤ λ i ≤ κ . y_{i}=x_{i}+\lambda_{i}\sigma_{i},\ \text{ 其中 } -\kappa\leq\lambda_{i}\leq\kappa. yi=xi+λiσi, 其中 −κ≤λi≤κ. (5)
因为那里不需要近似保持颜色饱和度。
3 稀疏(且难以察觉)攻击的算法
在本文中,我们提出了两种生成 l 0 l_{0} l0-、 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞ 和 l 0 + σ l_{0}+\sigma l0+σ-攻击的方法。第一种是基于分类器的 logits(神经网络在 softmax 层之前的输出)的随机化黑盒攻击。第二种是将 [21] 中关于正确标签损失的投影梯度下降 (PGD) 推广到我们不同的攻击模型。对于每种攻击模型,我们将推导出投影到相应集合上的算法。
基于分数的稀疏(且难以察觉)攻击
大多数现有的黑盒 l 0 l_{0} l0-攻击要么从扰动一小组像素开始,然后扩大这个集合直到找到对抗样本 [26, 24],要么在给定成功的对抗操作的情况下,尝试逐步减少用于改变分类的像素数量 [6, 28]。相反,我们引入了一种灵活的攻击方案,在开始时检查逐像素的目标攻击,然后根据分类器输出中产生的差距对它们进行排序。然后我们在排序列表上引入一个概率分布,并采样单像素更改以生成同时操纵多个像素的攻击。我们使用的分布偏向于那些单独应用时已经在分类器输出中产生较大变化的单像素扰动。在这种非迭代方案中,没有陷入次优点的危险。此外,虽然攻击必须测试许多点,但其非迭代性质允许以大批次检查扰动点,因此比进化攻击快得多。即使该方案简单,它的性能也优于所有现有方法,包括白盒攻击。
单像素修改 第一步,我们检查原始图像 x ∈ [ 0 , 1 ] d × 3 x\in[0,1]^{d\times 3} x∈[0,1]d×3(彩色)或 x ∈ [ 0 , 1 ] d x\in[0,1]^{d} x∈[0,1]d(灰度)的所有单像素修改。测试的修改取决于攻击模型。
- l 0 l_{0} l0-攻击: 对于每个像素 i i i,我们生成 8 = 2 3 8=2^{3} 8=23 个图像,将原始颜色值更改为 RGB 颜色立方体的 8 8 8 个角之一。因此我们将我们的方法命名为
CornerSearch 。这产生了一组 8 d 8d 8d 个图像,都是原始图像 x x x 的单像素修改,我们将其记为 ( z ( j ) ) j = 1 8 d (z^{(j)}){j=1}^{8d} (z(j))j=18d。对于灰度图像,只需检查极端灰度值(黑色和白色),得到 ( z ( j ) ) j = 1 2 d (z^{(j)}){j=1}^{2d} (z(j))j=12d。
-
l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击: 对于每个像素 i i i,我们生成 8 8 8 个图像,通过立方体 [ − ϵ , ϵ ] 3 [-\epsilon,\epsilon]^{3} [−ϵ,ϵ]3 的角来改变 ( x i j ) j = 1 3 (x_{ij}){j=1}^{3} (xij)j=13 的原始颜色值,再次得到 ( z ( j ) ) j = 1 8 d (z^{(j)}){j=1}^{8d} (z(j))j=18d 个图像。对于灰度图像,我们使用 x i ± ϵ x_{i}\pm\epsilon xi±ϵ,总共得到 ( z ( j ) ) j = 1 2 d (z^{(j)})_{j=1}^{2d} (z(j))j=12d 个图像。如果需要,我们进行裁剪以满足约束 z ( j ) ∈ [ 0 , 1 ] d × 3 z^{(j)}\in[0,1]^{d\times 3} z(j)∈[0,1]d×3 或 z ( j ) ∈ [ 0 , 1 ] d z^{(j)}\in[0,1]^{d} z(j)∈[0,1]d。
-
l 0 + σ l_{0}+\sigma l0+σ-map 攻击: 对于彩色图像,我们为每个像素 i i i 生成两个图像,通过设置 y i j = ( 1 ± κ σ i j ) x i j , j = 1 , ... , 3 , y_{ij}=(1\pm\kappa\sigma_{ij})x_{ij},\quad j=1,\ldots,3, yij=(1±κσij)xij,j=1,...,3, 其中 κ \kappa κ 和 σ i j \sigma_{ij} σij 如第 2 节所定义。对于灰度图像 x ∈ [ 0 , 1 ] d x\in[0,1]^{d} x∈[0,1]d,我们使用 y i = x i ± κ σ i . y_{i}=x_{i}\pm\kappa\sigma_{i}. yi=xi±κσi. 最后,我们将 y i j y_{ij} yij 和 y i y_{i} yi 裁剪到 [ 0 , 1 ] [0,1] [0,1]。因此,这产生了 ( z ( j ) ) j = 1 2 d (z^{(j)})_{j=1}^{2d} (z(j))j=12d 个图像。我们称之为 σ \sigma σ**-CornerSearch**。
生成所有图像后,我们获取每个图像的分类器输出 f ( z ( j ) ) j = 1 M f(z^{(j)}){j=1}^{M} f(z(j))j=1M,其中 M M M 是生成的图像总数,要么 M = 2 d M=2d M=2d,要么 M = 8 d M=8d M=8d。然后,对于每个类别 r ≠ c r\neq c r=c(其中 c = arg max r = 1 , ... , K f r ( x ) c=\arg\max\limits{r=1,\ldots,K}f_{r}(x) c=argr=1,...,Kmaxfr(x)),我们分别将值
f r ( z ( j ) ) − f c ( z ( j ) ) f_{r}(z^{(j)})-f_{c}(z^{(j)}) fr(z(j))−fc(z(j))
按递减顺序排序为 π ( r ) \pi^{(r)} π(r)。这意味着对于所有 1 ≤ s ≤ M − 1 1\leq s\leq M-1 1≤s≤M−1
f r ( z ( π s ( r ) ) ) − f c ( z ( π s ( r ) ) ) ≥ f r ( z ( π s + 1 ( r ) ) ) − f c ( z ( π s + 1 ( r ) ) ) . f_{r}(z^{(\pi_{s}^{(r)})})-f_{c}(z^{(\pi_{s}^{(r)})})\geq f_{r}(z^{(\pi_{s+1}^{(r )})})-f_{c}(z^{(\pi_{s+1}^{(r)})}). fr(z(πs(r)))−fc(z(πs(r)))≥fr(z(πs+1(r)))−fc(z(πs+1(r))).
我们还引入了一个顺序 π ( c ) \pi^{(c)} π(c),按递减顺序对量
max r ≠ c f r ( z ( j ) ) − f c ( z ( j ) ) \max_{r\neq c}f_{r}(z^{(j)})-f_{c}(z^{(j)}) r=cmaxfr(z(j))−fc(z(j))
进行排序。
生成这些单像素扰动的想法是识别那些最能将决策推向特定类别 r r r 的像素,或者对于集合 π ( c ) \pi^{(c)} π(c) 的情况,是推向非特定变化的像素。如果对于某个 r r r,有 f r ( z ( π 1 ( r ) ) ) − f c ( z ( π 1 ( r ) ) ) > 0 f_{r}(z^{(\pi_{1}^{(r)})})-f_{c}(z^{(\pi_{1}^{(r)})})>0 fr(z(π1(r)))−fc(z(π1(r)))>0,那么仅通过修改一个像素,决策就改变了。在这种情况下,算法立即停止。否则,可以尝试迭代地选择最有效的更改并重复单像素扰动。然而,这过于昂贵,并且如果在迭代方案的初始步骤中选择次优的像素修改,则会再次受到影响。因此,我们在下一段中提出一种基于所获得排序的采样方案,其中随机选择 k k k 个单像素修改进行组合以产生多像素攻击。
多像素修改 大多数时候,修改一个像素不足以改变决策。假设我们想通过更改最多 k k k 个像素来生成一个针对类别 r r r 的目标对抗样本候选,从根据排序 π ( r ) \pi^{(r)} π(r) 的前 N N N 个单像素扰动中选择。我们通过从 { 1 , ... , N } \{1,\ldots,N\} {1,...,N} 上的概率分布中采样 k k k 个索引 ( s 1 , ... , s k ) (s_{1},\ldots,s_{k}) (s1,...,sk) 来实现这一点,该分布定义为
P ( Z = i ) = 2 N − 2 i + 1 N 2 , i = 1 , ... , N . P(Z=i)=\frac{2N-2i+1}{N^{2}},\quad i=1,\ldots,N. P(Z=i)=N22N−2i+1,i=1,...,N. (6)
候选图像 y ( r ) y^{(r)} y(r) 是通过将图像 z ( π s 1 ( r ) ) , ... , z ( π s k ( r ) ) z^{(\pi_{s_{1}^{(r)})}},\ldots,z^{(\pi_{s_{k}^{(r)}})} z(πs1(r)),...,z(πsk(r)) 中定义的所有 k k k 个单像素更改应用于原始图像 x x x 而生成的。请注意,我们仅从上一段中找到的前 N N N 个单像素更改中采样,并且 { 1 , ... , N } \{1,\ldots,N\} {1,...,N} 上的分布偏向于采样列表的顶部,例如 P ( Z = 1 ) = 2 N − 1 N 2 P(Z=1)=\frac{2N-1}{N^{2}} P(Z=1)=N22N−1 是 P ( Z = N ) = 1 N 2 (Z=N)=\frac{1}{N^{2}} (Z=N)=N21 的 2 N − 1 2N-1 2N−1 倍。这种偏差确保我们主要累积那些单独应用时已经导致决策向目标类别 r r r 发生较大变化的单像素更改。我们为所有 K K K 个类别生成候选图像 y ( 1 ) , ... , y ( K ) y^{(1)},\ldots,y^{(K)} y(1),...,y(K),其中 K − 1 K-1 K−1 个候选图像针对特定类别的更改,一个图像攻击是非目标的(对于 r = c r=c r=c)。我们总共重复这个过程 N i t e r N_{iter} Niter 次。与迭代方案相比,采样方案的一大优势是所有这些图像都可以并行批量输入到分类器中,与顺序处理相比速度显著提高。此外,它不依赖于前面的步骤,因此不会陷入某些次优区域。如实验所示,这种相对简单的采样方案性能优于复杂的进化算法(黑盒攻击)甚至白盒攻击。
由于我们想要找到与 x x x 差异尽可能少像素的对抗样本,我们按照上述方法生成批次 y ( 1 ) , ... , y ( K ) y^{(1)},\ldots,y^{(K)} y(1),...,y(K) 的候选图像,逐渐增加 k k k,直到达到阈值 k max k_{\text{max}} kmax,直到我们得到一个与原始类别 c c c 不同的分类。算法 4 总结了主要步骤。
4 用于稀疏和难以察觉攻击的 PGD
Madry 等人 [21] 的投影梯度下降 (PGD) 攻击的目的不是找到最小的对抗扰动,而是从鲁棒优化的角度论证关于最大化损失
max z ∈ C ( x ) L ( c , f ( z ) ) , \max_{z\in C(x)}L(c,f(z)), z∈C(x)maxL(c,f(z)),
其中 L : { 1 , ... , K } × R K → R + L:\{1,\ldots,K\}\times\mathbb{R}^{K}\rightarrow\mathbb{R}_{+} L:{1,...,K}×RK→R+ 通常选择为交叉熵损失, c c c 是点 x x x 的正确标签,集合 C ( x ) ⊂ [ 0 , 1 ] d × 3 C(x)\subset[0,1]^{d\times 3} C(x)⊂[0,1]d×3(具有 d d d 个像素的彩色图像)或 C ( x ) ⊂ [ 0 , 1 ] d C(x)\subset[0,1]^{d} C(x)⊂[0,1]d(灰度图像)。从鲁棒优化的角度
的解释 [21] 导致了一种现在被广泛接受的对抗训练方式,目标是获得针对一组固定扰动的鲁棒性。在训练期间使用 PGD 攻击是对抗训练的事实标准,我们后面在第 5 节中也会使用。通常用作允许扰动集合的是 l ∞ l_{\infty} l∞-球: C ( x ) = { z ∣ ∥ z − x ∥ ∞ ≤ ϵ , z ∈ [ 0 , 1 ] d } C(x)=\{z\,|\,\|z-x\|_{\infty}\leq\epsilon,\,z\in[0,1]^{d}\} C(x)={z∣∥z−x∥∞≤ϵ,z∈[0,1]d},因为投影可以解析完成。
为了将 PGD 扩展到 l 0 l_{0} l0- 和 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击,我们首先必须捕获第 2 节中我们攻击模型中允许的集合,然后找到投影到这些集合上的快速算法。一旦这一点可用,PGD 就可以用作攻击和对抗训练。在附录中,我们还展示了如何投影到 l 0 l_{0} l0-球和由 σ \sigma σ-map 给出的分量约束的交集上,包括彩色和灰度图像。得益于此,我们可以引入 PGD 的 l 0 + σ l_{0}+\sigma l0+σ-map 版本,称为 σ \sigma σ-PGD,能够产生我们引入的稀疏且难以察觉的扰动。
投影到 l 0 l_{0} l0-球和 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-球上
给定一个原始彩色图像 x ∈ [ 0 , 1 ] d × 3 x\in[0,1]^{d\times 3} x∈[0,1]d×3,我们想要将一个给定点 y ∈ R d × 3 y\in\mathbb{R}^{d\times 3} y∈Rd×3 投影到集合
C ( x ) = { z ∈ R d × 3 | ∑ i = 1 d max j = 1 , 2 , 3 1 ∣ z i j − x i j ∣ > 0 ≤ k , l i j ≤ z i j ≤ u i j } C(x)=\left\{ z\in\mathbb{R}^{d\times 3} \;\middle|\; \sum_{i=1}^{d}\max_{j=1,2,3}\mathbf{1}{|z{ij}-x_{ij}|>0}\leq k,\ l_{ij}\leq z_{ij}\leq u_{ij} \right\} C(x)={z∈Rd×3 i=1∑dj=1,2,3max1∣zij−xij∣>0≤k, lij≤zij≤uij}
我们可以将投影到 C ( x ) C(x) C(x) 的问题写为
min z ∈ R d × 3 ∑ i = 1 d ∑ j = 1 3 ( y i j − z i j ) 2 \min_{z\in\mathbb{R}^{d\times 3}} \quad\sum_{i=1}^{d}\sum_{j=1}^{3}(y_{ij}-z_{ij})^{2} z∈Rd×3mini=1∑dj=1∑3(yij−zij)2 满足 l i j ≤ z i j ≤ u i j , i = 1 , ... , d , j = 1 , ... , 3 \quad l_{ij}\leq z_{ij}\leq u_{ij},\quad i=1,\ldots,d,\;j=1,\ldots,3 lij≤zij≤uij,i=1,...,d,j=1,...,3 ∑ i = 1 d max j = 1 , 2 , 3 1 ∣ z i j − x i j ∣ > 0 > 0 ≤ k \quad\sum_{i=1}^{d}\max_{j=1,2,3}{\bf 1}{|z{ij}-x_{ij}|>0}>0\leq k i=1∑dj=1,2,3max1∣zij−xij∣>0>0≤k
忽略组合约束,我们首先为每个像素 i i i 解决问题
min z i ∈ R 3 ∑ i = 1 d ∑ j = 1 3 ( y i j − z i j ) 2 \min_{z_{i}\in\mathbb{R}^{3}} \quad\sum_{i=1}^{d}\sum_{j=1}^{3}(y_{ij}-z_{ij})^{2} zi∈R3mini=1∑dj=1∑3(yij−zij)2 满足 l i j ≤ z i j ≤ u i j , i = 1 , ... , d , j = 1 , ... , 3 \quad l_{ij}\leq z_{ij}\leq u_{ij},\quad i=1,\ldots,d,\;j=1,\ldots,3 lij≤zij≤uij,i=1,...,d,j=1,...,3
解由 z i j ∗ = max { l i j , min { y i j , u i j } } z^{*}{ij}=\max\{l{ij},\min\{y_{ij},u_{ij}\}\} zij∗=max{lij,min{yij,uij}} 给出。我们注意到每个像素可以独立于其他像素进行优化。因此,我们按递减顺序 π \pi π 对每个像素 i i i 实现的收益
ϕ i : = ∑ j = 1 3 ( y i j − x i j ) 2 − ∑ j = 1 3 ( y i j − z i j ∗ ) 2 . \phi_{i}:=\sum_{j=1}^{3}(y_{ij}-x_{ij})^{2}-\sum_{j=1}^{3}(y_{ij}-z^{*}_{ij})^{2}. ϕi:=j=1∑3(yij−xij)2−j=1∑3(yij−zij∗)2.
进行排序。因此,最终解在具有最大收益的 k k k 个像素(或者如果具有正 ϕ i \phi_{i} ϕi 的像素少于 k k k 个,则更少)上与 x x x 不同,并由下式给出
z π , j = { z π , j ∗ 对于 i = 1 , ... , k , j = 1 , ... , 3 , x π , j 其他 . . z_{\pi,j}=\begin{cases}z^{*}{\pi,j}&\text{对于 }i=1,\ldots,k,\;j=1,\ldots,3,\\ x{\pi,j}&\text{其他}.\end{cases}. zπ,j={zπ,j∗xπ,j对于 i=1,...,k,j=1,...,3,其他..
使用 l i j = 0 l_{ij}=0 lij=0 和 u i j = 1 u_{ij}=1 uij=1,我们恢复了到 l 0 l_{0} l0-球和 [ 0 , 1 ] d × 3 [0,1]^{d\times 3} [0,1]d×3 交集的投影。对于 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞,注意两个约束
0 ≤ z i j ≤ 1 , − ϵ ≤ z i j − x i j ≤ ϵ , 0\leq z_{ij}\leq 1,\quad -\epsilon\leq z_{ij}-x_{ij}\leq\epsilon, 0≤zij≤1,−ϵ≤zij−xij≤ϵ,
等价于:
max { 0 , − ϵ + x i j } ≤ z i j ≤ min { 1 , x i j + ϵ } . \max\{0,-\epsilon+x_{ij}\}\leq z_{ij}\leq\min\{1,x_{ij}+\epsilon\}. max{0,−ϵ+xij}≤zij≤min{1,xij+ϵ}.
因此,通过使用
l i j = max { 0 , − ϵ + x i j } , u i j = min { 1 , x i j + ϵ } , l_{ij}=\max\{0,-\epsilon+x_{ij}\},\quad u_{ij}=\min\{1,x_{ij}+\epsilon\}, lij=max{0,−ϵ+xij},uij=min{1,xij+ϵ},
集合 C ( x ) C(x) C(x) 等于半径为 k k k 的 l 0 l_{0} l0-球、半径为 ϵ \epsilon ϵ 的 l ∞ l_{\infty} l∞-球(围绕 x x x)和 [ 0 , 1 ] d × 3 [0,1]^{d\times 3} [0,1]d×3 的交集。
5 实验
在实验部分,我们评估了我们基于分数的 l 0 l_{0} l0-攻击 CornerSearch 和我们白盒攻击 PGD({}{0}$ 的有效性。此外,我们给出了我们稀疏且难以察觉的 l 0 + σ l{0}+\sigma l0+σ-map 攻击 σ \sigma σ-CornerSearch 和 σ \sigma σ-PGD(后者在附录中)的说明性示例。最后,我们测试了关于各种范数的对抗训练作为对我们 l 0 l_{0} l0- 和 l 0 + σ l_{0}+\sigma l0+σ-map-攻击的防御。代码可在 https://github.com/fra31/sparse-imperceivable-attacks 获取。
l 0 l_{0} l0-攻击的评估
我们将 CornerSearch 与最先进的稀疏对抗扰动攻击进行比较:LocSearchAdv [24]、Pointwise Attack (PA) [28]、Carlini-Wagner l 0 l_{0} l0-attack (CW) [6]、SparseFool (SF) [22]、JSMA [26]。前两种在黑盒场景下操作,仅利用分类器输出,就像我们的方法一样,而后三种需要访问网络本身(白盒攻击)。注意 SparseFool 实际上是一种 l 1 l_{1} l1-攻击,这意味着它在 (1) 中使用 l 1 l_{1} l1-范数作为距离度量,以避免使用 l 0 l_{0} l0-范数产生的组合问题。然而,SparseFool 可以产生稀疏攻击,并且在 [22] 中显示在稀疏性方面优于 l 0 l_{0} l0-攻击。我们使用 [27] 中 Pointwise Attack 的实现,进行 10 次重启,如 [28] 中所做,CW 和 JSMA 来自 [25],同时我们重新实现了 SparseFool。由于 [24] 中使用的代码和模型都不可用(LocSearchAdv 的结果取自 [24]),我们决定在 [24] 报告的一种架构上比较不同攻击的性能,即在 MNIST 和 CIFAR-10 上重新训练的带批量归一化的 Network in Network [17]。
我们在相应测试集的前 1000 个点上运行攻击。我们使用 CornerSearch,参数为 k max = 50 k_{\text{max}}=50 kmax=50, N = 100 N=100 N=100 和 N iter = 1000 N_{\text{iter}}=1000 Niter=1000。在表 1 中,我们报告了每种方法的_成功率_,即可以成功攻击的正确分类点的比例,以及每次攻击需要修改以改变决策的像素的_均值_和_中位数_。请记住,MNIST 由 784 个像素的图像组成,CIFAR-10 由 1024 个像素组成。尽管 CornerSearch 并未为每个测试点找到对抗样本(因为我们固定了可以修改的最大像素数),但更改像素的平均数和中位数都低于其他方法,也就是说,我们的方法需要扰动的像素更少才能改变决策(唯一的例外是 MNIST 上的均值,但即使如此 CornerSearch 也具有更高的成功率和更低的中位数
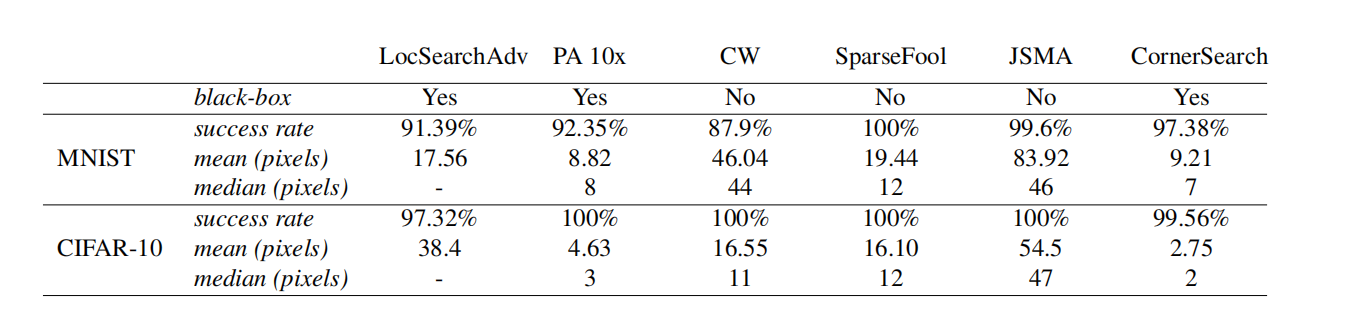
表 1:不同 l 0 l_{0} l0-攻击的比较。虽然 SparseFool 总是成功的,但它需要显著更多的像素被更改。我们的方法 CornerSearch 在所有攻击中需要更改的_中位数_像素量最少。
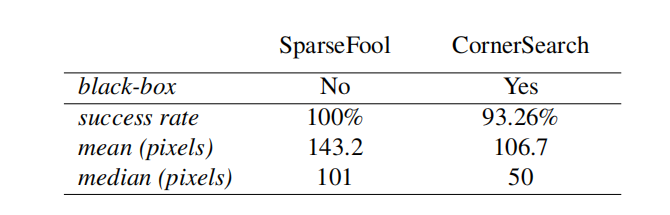
表 2:在 Restricted ImageNet 上的 l 0 l_{0} l0-攻击。 我们使用 SparseFool [22] 和我们的算法 CornerSearch 攻击验证集中 100 个点中正确分类的 89 个点。由于允许的像素更改数量限制,CornerSearch 并非总是成功,但需要更改的像素少得多。
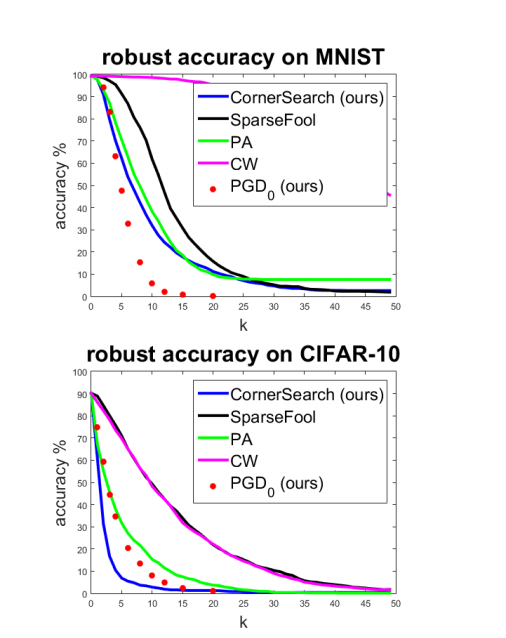
*图 2:*PGD({}_{0} 的评估。** 我们为 1000 个测试点计算了当攻击被允许扰动最多 k k k 个像素时分类器的鲁棒准确率。我们可以看到 PGD({}_{0}(红点)优于 SparseFool,因此是最好的"廉价"攻击,甚至在 MNIST 上对于 k ≥ 4 k\geq 4 k≥4 是最好的。
比 PA)。在 MNIST 上,CornerSearch 对于至少 50 % 50\% 50% 的所有测试图像需要更改 0.89 % 0.89\% 0.89% 的像素,而在 CIFAR-10 上甚至只有 0.2 % 0.2\% 0.2%。
利用第 4 节中关于投影到 l 0 l_{0} l0-球和 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-球上的推导,我们引入了著名 PGD 攻击的 l 0 l_{0} l0 版本,即 PGD 0 \text{PGD}_{0} PGD0。迭代方案(重复固定次数)是,给定一个分配给类别 c c c 的输入 x x x,
z ( i ) = x ( i − 1 ) + η ⋅ ∇ L ( c . f ( x ( i − 1 ) ) / ∥ ∇ L ( c . f ( x ( i − 1 ) ) ∥ 1 x ( i ) = P k ( z ( i ) ) , \begin{split} z^{(i)}&=x^{(i-1)}+\eta\cdot\nabla L(c.f(x^{(i-1)})/\|\nabla L(c.f(x^{(i-1)})\|{1}\\ x^{(i)}&=P{k}(z^{(i)}),\end{split} z(i)x(i)=x(i−1)+η⋅∇L(c.f(x(i−1))/∥∇L(c.f(x(i−1))∥1=Pk(z(i)), (7)
其中 η ∈ R + \eta\in\mathbb{R}{+} η∈R+, x ( 0 ) = x x^{(0)}=x x(0)=x, P k ( z ) P{k}(z) Pk(z) 表示投影到半径为 k k k 的 l 0 l_{0} l0-球上,以及由框约束 x ∈ [ 0 , 1 ] d x\in[0,1]^{d} x∈[0,1]d 定义的 l ∞ l_{\infty} l∞-球。注意 PGD 0 \text{PGD}{0} PGD0 需要指定 k k k,因此不像 (1) 那样旨在进行最小修改来改变决策。为了评估鲁棒准确率,即当攻击者的目标是使用 k k k-像素修改改变所有正确分类图像的决策时分类器的准确率,需要为每个 k k k 值分别评估 PGD 0 \text{PGD}{0} PGD0,而所有其他攻击在一次运行中产生所有稀疏度级别的鲁棒准确率。
为了比较,我们在表 1 的网络(更多细节见附录)上使用 20 次迭代和 10 次随机重启运行 PGD 0 \text{PGD}{0} PGD0,使用 10 个稀疏值 k k k。在图 2 中,我们显示了不同攻击的鲁棒准确率。 PGD 0 \text{PGD}{0} PGD0 在 MNIST 上对于 k ≥ 4 k\geq 4 k≥4 取得了最佳结果,优于 SparseFool,甚至在 CIFAR-10 上接近 CornerSearch。由于 PGD 0 \text{PGD}_{0} PGD0 非常快,它是我们更昂贵的基于分数攻击的一个有价值的替代方案。
我们进一步在 Restricted ImageNet 上测试 CornerSearch,这是 ImageNet [10] 的一个子集,其中一些类别被分组形成 9 个不同的宏类。我们使用 [31] 中的 ResNet-50,并将我们的攻击与 SparseFool [22] 进行比较(我们不运行其他方法,因为要么没有可用的代码,要么它们无法扩展到图像的大小)。图像有 50176 个像素。
在表 2 中,我们报告了在 100 个点上 SparseFool 和我们的攻击(参数为 k max = 1000 , N iter = 1000 k_{\text{max}}=1000,N_{\text{iter}}=1000 kmax=1000,Niter=1000)的统计数据。与其他数据集一样,SparseFool 总是找到对抗样本,而最小的_均值_和_中位数_对抗修改是由 CornerSearch 实现的,尽管成功率较低。SparseFool 的运行时间比 CornerSearch 快约 55 倍。我们的攻击的运行时间直接与像素数和网络的前向传递时间成正比,在这种情况下两者都很大。但是,请注意 SparseFool 是白盒攻击,而我们的的是黑盒攻击。与 PGD 0 \text{PGD}{0} PGD0 比较,给定 100 个像素的预算,SF 的成功率为 49.4%,CS 为 64.0%, PGD 0 \text{PGD}{0} PGD0 为 39.3%。
稀疏且难以察觉的操纵
我们说明了由 l 0 l_{0} l0-、 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞- 和 l 0 + σ l_{0}+\sigma l0+σ-map 攻击找到的对抗修改之间的差异。在图 3 和图 4 中,我们展示了一些例子。如前所述,仅关于 l 0 l_{0} l0-范数产生的对抗修改是最稀疏的,但也最容易识别。 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击提供的图像,虽然个体修改的绝对值是有界的(这里我们对 CIFAR-10 使用 δ = 0.1 \delta=0.1 δ=0.1,对 ImageNet 使用 δ = 0.05 \delta=0.05 δ=0.05),但一些扰动是可见的,因为要么颜色与邻居不均匀(图 3 左侧和第二行以及图 4 右侧的第二行),要么在均匀背景中引入了修改(图 3 右侧的第二行和图 4 左侧的第二行)。另一方面, σ \sigma σ-CornerSearch 的对抗修改难以察觉,同时仍然非常稀疏(图 3 和图 4 的第三行),表明 σ \sigma σ-map(在图中也显示,重新缩放使得最大分量等于 1)能够正确识别难以察觉变化的区域(特别是参见放大的图像)。
我们在附录中提供了由 σ \sigma σ-CornerSearch 和 σ \sigma σ-PGD 制作的对抗样本的比较。
对抗训练
为了增加模型对稀疏对抗操纵的鲁棒性,我们将对抗训练适应于我们的情况。我们使用上面介绍的 PGD 0 \text{PGD}{0} PGD0 进行对抗训练,以实现针对 l 0 l{0} l0-攻击的鲁棒性( l 0 l_{0} l0-at ),同时我们使用 σ \sigma σ-PGD 来增强针对
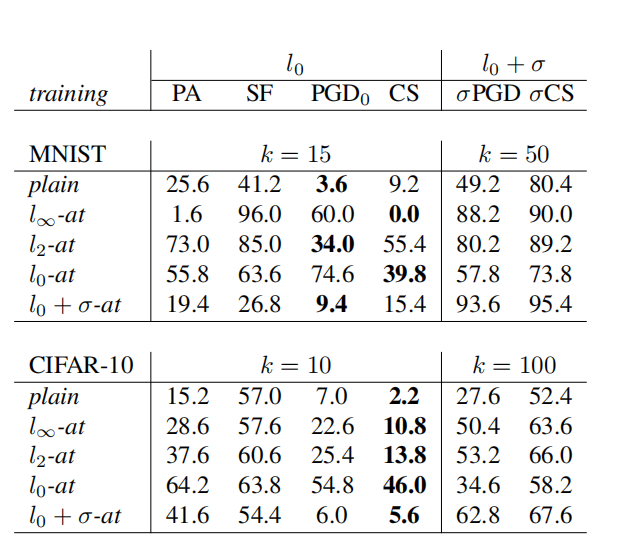
表 3:对抗训练的评估。 由 l 0 l_{0} l0- 和 l 0 + σ l_{0}+\sigma l0+σ-攻击(最多更改 k k k 个像素,对于 l 0 + σ l_{0}+\sigma l0+σ-攻击,固定 MNIST 的 κ = 0.8 \kappa=0.8 κ=0.8 和 CIFAR-10 的 κ = 0.4 \kappa=0.4 κ=0.4)在针对不同度量进行对抗训练的模型上给出的鲁棒准确率(%)。
稀疏且难以察觉攻击的鲁棒性( l 0 + σ l_{0}+\sigma l0+σ-at )。使用这两种技术,我们在 MNIST 和 CIFAR-10 上训练模型(关于架构和超参数的更多细节在附录中)。我们将它们与在_普通_训练集上训练的模型以及关于 l ∞ l_{\infty} l∞- 和 l 2 l_{2} l2-范数进行对抗训练的模型( l ∞ l_{\infty} l∞-at 和 l 2 l_{2} l2-at )进行比较。在表 3 中,我们报告了在 500 个点上的鲁棒准确率(我们固定要修改的最大像素数为 k k k,并且 (4) 和 (5) 中定义的 l 0 + σ l_{0}+\sigma l0+σ 攻击的参数对于 MNIST 固定为 κ = 0.8 \kappa=0.8 κ=0.8,对于 CIFAR-10 固定为 κ = 0.4 \kappa=0.4 κ=0.4)。
在 MNIST 上,针对 l 2 l_{2} l2 和 l 0 l_{0} l0 扰动训练的模型对 l 0 l_{0} l0-攻击最具鲁棒性,而在 CIFAR-10 上, l 0 l_{0} l0-at 模型的抵抗力是所有其他模型的三倍多。与 [22] 类似,我们发现 l ∞ l_{\infty} l∞-at 对 l 0 l_{0} l0-鲁棒性没有帮助。值得注意的是,在两个数据集上,我们的攻击 PGD({}_{0}$ 和 CornerSearch (CS) 取得了最好的结果,因此是最适合评估鲁棒性的方法。
关于 l 0 + σ l_{0}+\sigma l0+σ-map 攻击,我们看到 l 0 + σ l_{0}+\sigma l0+σ-at 模型最不容易受到攻击,但 l ∞ l_{\infty} l∞-at 和 l 2 l_{2} l2-at 也显示出一定的鲁棒性。注意 σ \sigma σ-PGD 比 σ \sigma σ-CornerSearch 更成功,但产生的扰动稀疏性较低,因为它总是充分利用要修改的 k k k 个像素的预算,而 σ \sigma σ-CS 大多只使用其中的几个,使得修改更难以被发现(见附录)。

图 3:在 CIFAR-10 上的不同攻击。 我们说明了由 CornerSearch ( l 0 l_{0} l0)、 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击 和 σ \sigma σ-CornerSearch 找到的对抗样本(第二列)的差异,分别是第一、第二和第三行。第三列显示了重新缩放到 [ 0 , 1 ] [0,1] [0,1] 的对抗扰动,第四列是修改像素的映射(_稀疏性_列)。原始图像可以在左上角找到, σ \sigma σ-map 的 RGB 表示在左下角。
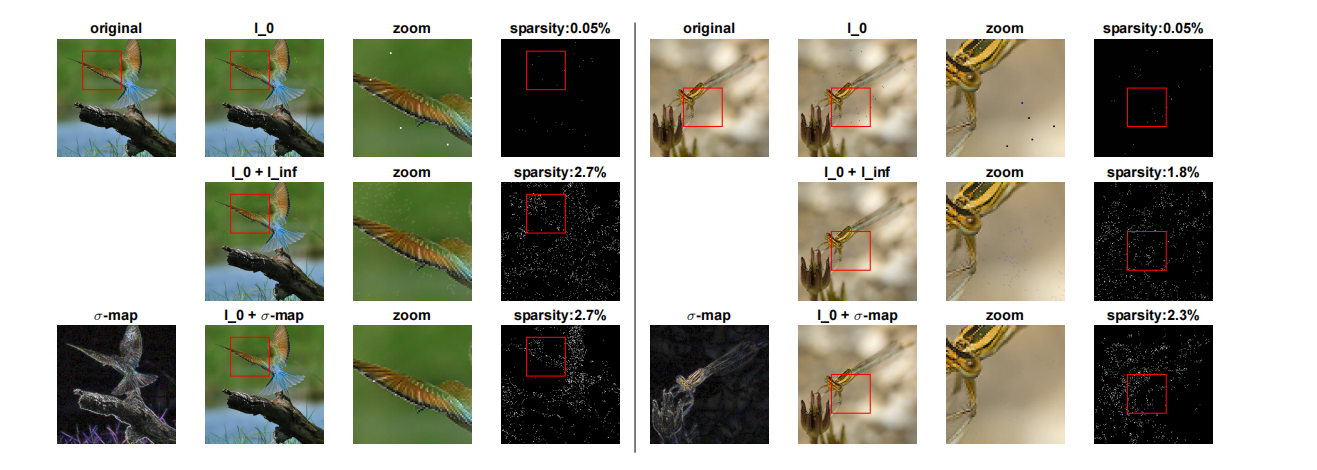
图 4:在 Restricted ImageNet 上的不同攻击。 我们说明了由 CornerSearch ( l 0 l_{0} l0)、 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击 和 σ \sigma σ-CornerSearch 找到的对抗样本(第二列,第三列放大)的差异,分别是第一、第二和第三行。第四列显示了修改像素的映射(_稀疏性_列)。原始图像在左上角,重新缩放的 σ \sigma σ-map 的 RGB 表示在左下角。
致谢
由德国研究基金会 (DFG) 卓越集群 Machine Learning: New Perspectives for Science, EXC 2064/1, 项目编号 390727645 资助,并作为 TRR 248 的一部分由 DFG 资助 389792660 资助。
参考文献
-
1\] Anish Athalye, Nicholas Carlini, and David Wagner. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. *arXiv preprint arXiv:1802.00420*, 2018.
-
3\] Battista Biggio, Igino Corona, Davide Maiorca, Blaine Nelson, Nedim Srndic, Pavel Laskov, Giorgio Giacinto, and Fabio Roli. Evasion attacks against machine learning at test time. In *ECML PKDD*, 2013.
-
5\] Nicholas Carlini and David A. Wagner. Adversarial examples are not easily detected: Bypassing ten detection methods. In *ACM Workshop on Artificial Intelligence and Security*, 2017.
-
7\] Pin-Yu Chen, Huan Zhang, Yash Sharma, Jinfeng Yi, and Cho-Jui Hsieh. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In *10th ACM Workshop on Artificial Intelligence and Security (AISEC)*, 2017.
-
9\] Nilesh N. Dalvi, Pedro M. Domingos, Mausam, Sumit K. Sanghai, and Deepak Verma. Adversarial classification. In *KDD*, 2004.
-
11\] Ivan Evtimov, Kevin Eykholt, Earlence Fernandes, Tadayoshi Kohno, Bo Li, Atul Prakash, Amir Rahmati, and Dawn Song. Robust physical-world attacks on deep learning visual classification. In *CVPR*, 2018.
-
13\] Andrew Ilyas, Logan Engstrom, Anish Athalye, and Jessy Lin. Black-box adversarial attacks with limited queries and information. In *ICML*, 2018.
-
15\] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. preprint, arXiv:1412.6980, 2014.
-
17\] Min Lin, Qiang Chen, and Shuicheng Yan. Network in network. In *ICLR*, 2014.
-
19\] Daniel Lowd and Christopher Meek. Adversarial learning. In *KDD*, 2005.
-
21\] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. In *ICLR*, 2018.
-
23\] Seyed-Mohsen Moosavi-Dezfooli, Alhussein Fawzi, and Pascal Frossard. Deepfool: a simple and accurate method to fool deep neural networks. In *CVPR*, pages 2574--2582, 2016.
-
25\] Nicolas Papernot, Fartash Faghri, Nicholas Carlini, Ian Goodfellow, Reuben Feinman, Alexey Kurakin, Cihang Xie, Yash Sharma, Tom Brown, Aurko Roy, Alexander Matyasko, Vahid Behzadan, Karen Hambardzumyan, Zhishuai Zhang, Yi-Lin Juang, Zhi Li, Ryan Sheatsley, Abhibhav Garg, Jonathan Uesato, Willi Gierke, Yinpeng Dong, David Berthelot, Paul Hendricks, Jonas Rauber, and Rujun Long. cleverhans v2.0.0: an adversarial machine learning library. preprint, arXiv:1610.00768, 2017.
-
27\] Jonas Rauber, Wieland Brendel, and Matthias Bethge. Foolbox: A python toolbox to benchmark the robustness of machine learning models. In *ICML Reliable Machine Learning in the Wild Workshop*, 2017.
-
29\] Jiawei Su, Danilo Vasconcellos Vargas, and Kouichi Sakurai. One pixel attack for fooling deep neural networks. *arXiv preprint arXiv:1710.08864v5*, 2019.
-
31\] Dimitris Tsipras, Shibani Santurkar, Logan Engstrom, Alexander Turner, and Aleksander Madry. Robustness may be at odds with accuracy. In *ICLR*, 2019.
-
32\] Chaowei Xiao, Jun-Yan Zhu, Bo Li, Warren He, Mingyan Liu, and Dawn Song. Spatially transformed adversarial examples. In *ICLR*, 2018.
我们在这里介绍用于 σ \sigma σ-PGD 攻击的投影步骤,其中我们允许最多 k k k 个像素上的扰动并尊重 (4) 和 (5) 中定义的 σ \sigma σ-map 约束。
彩色图像
给定一个彩色图像 x ∈ [ 0 , 1 ] d × 3 x\in[0,1]^{d\times 3} x∈[0,1]d×3,我们想要将一个给定点 y ∈ R d × 3 y\in\mathbb{R}^{d\times 3} y∈Rd×3 投影到集合
C ( x ) = { z ∈ R d × 3 | ∑ i = 1 d max j = 1 , 2 , 3 1 { ∣ z i j − x i j ∣ > 0 } ≤ k , ( 1 − κ σ i j ) x i j ≤ z i j ≤ ( 1 + κ σ i j ) x i j , 0 ≤ z i j ≤ 1 for all i , j } C(x) = \left\{ z \in \mathbb{R}^{d \times 3} \;\middle|\; \begin{array}{l} \displaystyle \sum_{i=1}^{d} \max_{j=1,2,3} \mathbb{1}{\{|z{ij} - x_{ij}| > 0\}} \leq k, \\ (1-\kappa\sigma_{ij})x_{ij} \leq z_{ij} \leq (1+\kappa\sigma_{ij})x_{ij}, \\ 0 \leq z_{ij} \leq 1 \quad \text{for all } i,j \end{array} \right\} C(x)=⎩ ⎨ ⎧z∈Rd×3 i=1∑dj=1,2,3max1{∣zij−xij∣>0}≤k,(1−κσij)xij≤zij≤(1+κσij)xij,0≤zij≤1for all i,j⎭ ⎬ ⎫
其中 d d d 是像素数, σ i j \sigma_{ij} σij 是第 2 节中定义的逐像素、通道特定的界限, κ > 0 \kappa>0 κ>0 是给定参数。我们可以将投影问题写为
min λ ∈ R d ∑ i = 1 d ∑ j = 1 3 ( y i j − ( 1 + λ i σ i j ) x i j ) 2 \min_{\lambda\in\mathbb{R}^{d}} \quad\sum_{i=1}^{d}\sum_{j=1}^{3}(y_{ij}-(1+\lambda_{i}\sigma_{ij} )x_{ij})^{2} λ∈Rdmini=1∑dj=1∑3(yij−(1+λiσij)xij)2 满足 − κ ≤ λ i ≤ κ , i = 1 , ... , d \quad -\kappa\leq\lambda_{i}\leq\kappa,\quad i=1,\dots,d −κ≤λi≤κ,i=1,...,d
0 ≤ ( 1 + λ i σ i j ) x i j ≤ 1 , i = 1 , ... , d , j = 1 , ... , 3 \quad 0\leq(1+\lambda_{i}\sigma_{ij})x_{ij}\leq 1,\;i=1,\dots,d,\, j=1,\dots,3 0≤(1+λiσij)xij≤1,i=1,...,d,j=1,...,3
∑ i = 1 d 1 ∣ λ i ∣ > 0 ≤ k \quad\sum_{i=1}^{d}\mathbb{1}{|\lambda{i}|>0}\leq k i=1∑d1∣λi∣>0≤k
忽略组合约束,我们首先为每个像素解决问题
min λ i ∈ R ∑ j = 1 3 ( y i j − ( 1 + λ i σ i j ) x i j ) 2 \min_{\lambda_{i}\in\mathbb{R}} \quad\sum_{j=1}^{3}(y_{ij}-(1+\lambda_{i}\sigma_{ij})x_{ij})^{2} λi∈Rminj=1∑3(yij−(1+λiσij)xij)2 满足 − κ ≤ λ i ≤ κ \quad -\kappa\leq\lambda_{i}\leq\kappa −κ≤λi≤κ 0 ≤ ( 1 + λ i σ i j ) x i j ≤ 1 , j = 1 , ... , 3 \quad 0\leq(1+\lambda_{i}\sigma_{ij})x_{ij}\leq 1,\quad j=1,\dots,3 0≤(1+λiσij)xij≤1,j=1,...,3
我们首先注意到,如果 x i j = 0 x_{ij}=0 xij=0 或 σ i j = 0 \sigma_{ij}=0 σij=0,最后一个约束总是满足。在其他情况下,我们可以将约束重写为
− 1 σ i j ≤ λ i ≤ 1 σ i j ( 1 x i j − 1 ) , j = 1 , ... , 3. -\frac{1}{\sigma_{ij}}\;\leq\;\lambda_{i}\;\leq\;\frac{1}{\sigma_{ij}}\Big(\frac{1}{x_{ij}}-1\Big),\quad j=1,\dots,3. −σij1≤λi≤σij1(xij1−1),j=1,...,3.
结合所有约束得到
λ i ( l ) : = max { − κ , max x i j ≠ 0 , σ i j ≠ 0 ( − 1 σ i j ) } ≤ λ i ≤ min { κ , min x i j ≠ 0 , σ i j ≠ 0 1 σ i j ( 1 x i j − 1 ) } : = λ i ( u ) . \lambda_{i}^{(l)} :=\max\left\{-\kappa,\max_{x_{ij}\neq 0,\sigma_{ij}\neq 0}\left(-\frac{1}{\sigma_{ij}}\right)\right\}\;\leq\;\lambda_{i} \qquad\leq\;\min\left\{\kappa,\min_{x_{ij}\neq 0,\sigma_{ij}\neq 0}\frac{1}{\sigma_{ij}}\left(\frac{1}{x_{ij}}-1\right)\right\}:=\lambda_{i}^{(u)}. λi(l):=max{−κ,xij=0,σij=0max(−σij1)}≤λi≤min{κ,xij=0,σij=0minσij1(xij1−1)}:=λi(u).
无约束解由下式给出
λ i ⋆ = ∑ j = 1 3 σ i j x i j ( y i j − x i j ) ∑ j = 1 3 σ i j 2 x i j 2 . \lambda_{i}^{\star}=\frac{\sum_{j=1}^{3}\sigma_{ij}x_{ij}(y_{ij}-x_{ij})}{\sum_ {j=1}^{3}\sigma_{ij}^{2}x_{ij}^{2}}. λi⋆=∑j=13σij2xij2∑j=13σijxij(yij−xij).
因此,每个像素 i i i 的最优解由下式给出
λ i ⋆ = max { λ i ( l ) , min { λ i ′ , λ i ( u ) } } . \lambda_{i}^{\star}=\max\{\lambda_{i}^{(l)},\min\{\lambda_{i}^{\prime},\lambda _{i}^{(u)}\}\}. λi⋆=max{λi(l),min{λi′,λi(u)}}.
原始问题的最终解只允许选择 k k k 个像素进行更改。对于每个像素 i i i,量
ϕ i : = ∑ j = 1 3 ( y i j − x i j ) 2 − ∑ j = 1 3 ( y i j − ( 1 + λ i ⋆ σ i j ) x i j ) 2 \phi_{i}:=\sum_{j=1}^{3}(y_{ij}-x_{ij})^{2}-\sum_{j=1}^{3}(y_{ij}-(1+\lambda_{i }^{\star}\sigma_{ij})x_{ij})^{2} ϕi:=j=1∑3(yij−xij)2−j=1∑3(yij−(1+λi⋆σij)xij)2
表示在 λ i = 0 \lambda_{i}=0 λi=0(即 y i y_{i} yi 被投影到 x i x_{i} xi)和 λ i = λ i ⋆ \lambda_{i}=\lambda_{i}^{\star} λi=λi⋆ 两种情况之间目标函数增加量的差异。由于我们想要最小化目标函数,最优解是通过将 ( ϕ i ) i = 1 d (\phi_{i})_{i=1}^{d} (ϕi)i=1d 按递减顺序 π \pi π 排序并设置
λ π i ( f i n a l ) = { λ π i ⋆ 如果 i = 1 , ... , k , 0 其他 . . \lambda_{\pi_{i}}^{(final)}=\begin{cases}\lambda_{\pi_{i}}^{\star}&\text{如果 }i =1,\dots,k,\\ 0&\text{其他}.\end{cases}. λπi(final)={λπi⋆0如果 i=1,...,k,其他..
最后, y y y 被投影到的属于 C ( x ) C(x) C(x) 的点是 z ∈ R d × 3 z\in\mathbb{R}^{d\times 3} z∈Rd×3,其分量定义为
z i j = ( 1 + λ i ( f i n a l ) σ i j ) x i j , i = 1 , ... , d , j = 1 , ... , 3. z_{ij}=(1+\lambda_{i}^{(final)}\sigma_{ij})x_{ij},\;i=1,\dots,d,\;j=1,\dots,3. zij=(1+λi(final)σij)xij,i=1,...,d,j=1,...,3.
灰度图像
由于灰度图像只有一个颜色通道,并且为了获得难以察觉的操纵,我们使用 (5) 中定义的加法修改,我们投影到集合上,给定原始图像 x x x,
C ( x ) = { z ∈ R d ∣ ∑ i = 1 d 1 ∣ z i − x i ∣ > 0 ≤ k , x i − κ σ i ≤ z i ≤ x i + κ σ i , 0 ≤ z i ≤ 1 } . C(x)=\left\{z\in\mathbb{R}^{d} \mid \sum_{i=1}^{d}\mathbb{1}{|z{i}- x_{i}|>0}\leq k,\ x_{i}-\kappa\sigma_{i}\leq z_{i}\leq x_{i}+\kappa\sigma_{i},\ 0\leq z_{i}\leq 1\right\}. C(x)={z∈Rd∣i=1∑d1∣zi−xi∣>0≤k, xi−κσi≤zi≤xi+κσi, 0≤zi≤1}.
定义
l i : = max { x i − κ σ i , 0 } , u i : = min { x i + κ σ i , 1 } , l_{i}:=\max\{x_{i}-\kappa\sigma_{i},0\},\quad u_{i}:=\min\{x_{i}+\kappa\sigma_{ i},1\}, li:=max{xi−κσi,0},ui:=min{xi+κσi,1},
我们可以看出,在这种情况下,问题等价于投影到 l 0 l_{0} l0-球和框约束的交集上,然后按照第 4.1 节所述进行求解。
受攻击模型的测试准确率
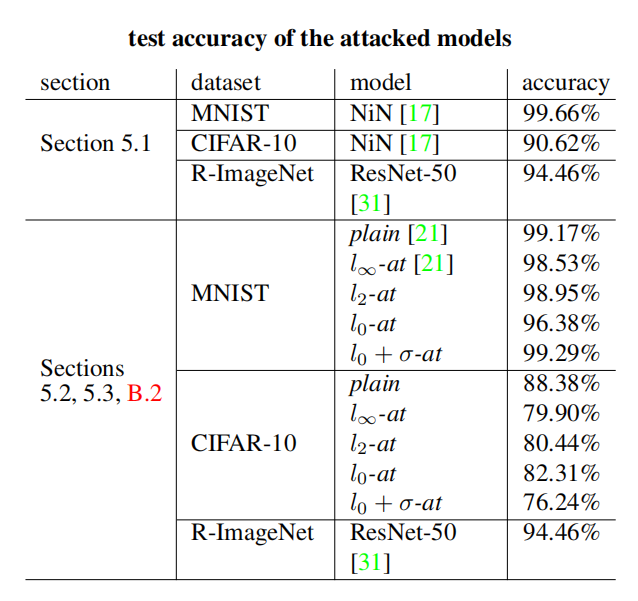
表 4:受攻击模型的准确率。 我们在这里报告第 5 节介绍的模型在测试集(对于 Restricted ImageNet 是验证集)上的准确率。
附录 B 实验
我们在这里报告第 5 节中关于攻击、受攻击模型和参数的详细信息。论文中介绍的每个模型在测试集(对于 Restricted ImageNet 是验证集)上的准确率在表 4 中报告。
l 0 l_{0} l0-攻击的评估
本实验使用的架构是 [17] 中的 Network in Network,我们根据 https://github.com/BIGBALLON/cifar-10-cnn 上可用的代码进行训练,并将其适应于 MNIST(具有不同的输入维度)的情况。
我们运行 PGD({}_{0}$,使用十个阈值 k k k(即可以修改的最大像素数),对于 MNIST, k ∈ { 2 , 3 , 4 , 5 , 6 , 8 , 10 , 12 , 15 , 20 } k\in \{2,3,4,5,6,8,10,12,15,20\} k∈{2,3,4,5,6,8,10,12,15,20},对于 CIFAR-10, k ∈ { 1 , 2 , 3 , 4 , 6 , 8 , 10 , 12 , 15 , 20 } k\in \{1,2,3,4,6,8,10,12,15,20\} k∈{1,2,3,4,6,8,10,12,15,20}。
运行时间 我们报告第 5.1 节实验中一张图像的平均运行时间(SparseFool 的时间来自我们的重新实现,它使用 [27] 中实现的 DeepFool)。MNIST:LocSearchAdv 0.6s(来自 [25]),PA 21s,CW 300s,SparseFool 2.5s,CornerSearch 9.8s,PGD({}*{0} 0.06s(一个阈值)。CIFAR-10:LocSearchAdv 0.7s \[25\],PA 22s,CW 283s,SparseFool 1.0s,CornerSearch 3.6s,PGD({}*{0} 0.19s(一个阈值)。ImageNet:SparseFool 17s,CornerSearch 953s,PGD({}_{0}$ 13s(一个阈值)。
CornerSearch 的稳定性 由于算法 1 涉及随机采样组件,我们想在这里分析 CornerSearch 的性能如何依赖于它。然后,我们在表 1 使用的模型上运行 CornerSearch 10 次,得到以下统计数据:MNIST,成功率 (%) 97.37 ± 0.13 97.37\pm 0.13 97.37±0.13,均值 9.12 ± 0.05 9.12\pm 0.05 9.12±0.05,中位数 7 ± 0 7\pm 0 7±0 。CIFAR-10,成功率 (%) 99.33 ± 0.12 99.33\pm 0.12 99.33±0.12,均值 2.71 ± 0.02 2.71\pm 0.02 2.71±0.02,中位数 2 ± 0 2\pm 0 2±0。这意味着我们的攻击在不同运行之间是稳定的。
稀疏且难以察觉的操纵
在图 5 中,我们展示了一个例子,说明即使颜色与某些相邻像素相似,沿轴对齐边缘的更改也是明显且易于检测的。这为我们用于决定图像在何处可以以不可见方式扰动的启发式方法提供了进一步的正当理由。
在图 6、7 和 8 中,我们说明了 l 0 + σ l_{0}+\sigma l0+σ-map 攻击如何产生稀疏且难以察觉的对抗扰动,而 l 0 l_{0} l0- 和 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击要么引入与邻居颜色不均匀的颜色,要么修改均匀背景中的像素,这使得它们很容易被看到。更多示例可以在 https://github.com/fra31/sparse-imperceivable-attacks 找到。
MNIST 在图 6 中,我们展示了我们的攻击 CornerSearch ( l 0 l_{0} l0-攻击)、 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击 和 σ \sigma σ-CornerSearch 找到的对抗样本之间的差异。我们看到我们的 l 0 + σ l_{0}+\sigma l0+σ-map 攻击不会修改背景中、远离数字或数字内部均匀颜色区域中的像素。
受攻击的模型是第 5.3 节中的_普通_模型(关于架构的更多细节见下文)。对于 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击,我们使用扰动的 l ∞ l_{\infty} l∞-范数界限 δ = 0.2 \delta=0.2 δ=0.2。
CIFAR-10 我们在图 7 中展示了更多按照第 5 节图 3 方式构建的示例。受攻击的模型是第 5.3 节中的_普通_分类器(关于架构的更多细节见下文)。对于 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击,我们使用扰动的 l ∞ l_{\infty} l∞-范数界限 δ = 0.1 \delta=0.1 δ=0.1。

图 5:左:原始图像。右: l 0 l_{0} l0-对抗样本,沿轴对齐边缘的更改清晰可见。
Restricted ImageNet 我们在图 8 中展示了更多按照第 5 节图 4 方式创建的示例。受攻击的模型是 [31] 中的 ResNet-50(权重和代码均可在 https://github.com/MadryLab/robust-features-code 获取),已在第 5.1 节中介绍。对于 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击,我们使用 δ = 0.05 \delta=0.05 δ=0.05 作为扰动的 l ∞ l_{\infty} l∞-范数界限。
对抗训练
MNIST 使用的架构与 [21] 中的相同(可在 https://github.com/MadryLab/mnist_challenge 获取),包括 2 个卷积层,每个后面跟着一个最大池化操作,以及 2 个密集层。我们使用 Adam [15] 训练我们的分类器 100 个周期。
普通 和 l ∞ l_{\infty} l∞-at 模型是 [21] 在 https://github.com/MadryLab/mnist_challenge 提供的,而我们使用普通梯度作为 PGD 更新的方向来训练 l 2 l_{2} l2-at ,与用于关于 l ∞ l_{\infty} l∞-范数的对抗训练的梯度符号相反。
对于关于 l 0 l_{0} l0-范数的对抗训练,我们使用 k = 20 k=20 k=20(要更改的最大像素数),40 次迭代,步长 η = 30000 / 255 \eta=30000/255 η=30000/255。对于 l 0 + σ l_{0}+\sigma l0+σ-at ,我们设置 k = 100 k=100 k=100, κ = 0.9 \kappa=0.9 κ=0.9(对于 σ \sigma σ-map 给出的界限),40 次梯度下降迭代,步长 η = 30000 / 255 \eta=30000/255 η=30000/255。
CIFAR-10 我们使用一个具有 8 个卷积层的 CNN,分别包含 96, 96, 192, 192, 192, 192, 192 和 384 个特征图,以及 2 个密集层,分别为 1200 和 10 个单元。除最后一层外,在每个层的输出上应用 ReLU 激活函数。我们使用数据增强(特别是应用随机裁剪和随机镜像)进行 100 个周期的训练,并使用 Adam 优化器 [15]。
对于关于 l 0 l_{0} l0-范数的对抗训练,我们使用 k = 20 k=20 k=20(要更改的像素数),10 次 PGD 迭代,步长 η = 30000 / 255 \eta=30000/255 η=30000/255。对于 l 0 + σ l_{0}+\sigma l0+σ-at ,我们使用 k = 120 k=120 k=120, κ = 0.6 \kappa=0.6 κ=0.6,10 次 PGD 迭代,步长 η = 30000 / 255 \eta=30000/255 η=30000/255。
附录 C σ \sigma σ-PGD 的对抗样本
我们想在这里比较我们的两种方法 σ \sigma σ-CornerSearch 和 σ \sigma σ-PGD 生成的对抗样本。在图 9 和 10 中(另见 https://github.com/fra31/sparse-imperceivable-attacks),我们展示了两种攻击产生的扰动图像,以及原始图像和重新缩放的修改(使得每个分量在 [0,1] 内且最大分量等于 1)。此外,对于 σ \sigma σ-PGD,我们报告了使用较小 κ \kappa κ 获得的结果。灰色图像表示不成功的情况。
很明显, σ \sigma σ-CornerSearch 产生更稀疏的扰动。此外,使用与 σ \sigma σ-CS 相同 κ \kappa κ 的 σ \sigma σ-PGD 会产生更明显的操纵。我们认为这有两个原因:首先, σ \sigma σ-PGD 总是使用要修改的 k k k 个像素的整个预算,而 σ \sigma σ-CS 不会这样;其次, σ \sigma σ-PGD 旨在允许扰动空间内最大化损失。这可能是通过修改相邻像素(有时颜色略有不同)以相反方向(即对于不同的 i i i, λ i \lambda_{i} λi 符号不同)来实现的。相反, σ \sigma σ-CornerSearch 不考虑像素之间的空间关系,因此不会表现出这种行为。然而,如图所示,通过减小 κ \kappa κ 也可以恢复 σ \sigma σ-PGD 的不太明显的变化,但代价是成功率较低。
附录 D 稀疏扰动的传播
为了可视化非常稀疏的扰动对分类器所做决策的影响,我们可以检查当对抗样本作为网络输入而不是原始图像时,每个隐藏层的输出如何被修改。我们在这里考虑第 5 节中不同对抗训练方案比较中使用的 CIFAR-10 上的_普通_模型以及 CornerSearch 在其上生成的对抗样本。
我们首先使用原始图像作为输入执行前向传递,然后使用对抗性操纵的图像执行前向传递。在图 11 中(更多示例在 https://github.com/fra31/sparse-imperceivable-attacks),我们绘制了(每种颜色代表测试集中的一张图像)两次前向传递获得的网络每个单元在激活函数后的输出值之间的差异。垂直线段分隔各层,最左边的部分显示输入的差异。水平线表示两次前向传递之间值没有差异。我们可以看到,随着网络深入(在图 11 中向右),修改的稀疏性降低(输入的被扰动分量平均为 0.21%,最后一个隐藏层的为 19.45%),而它们的幅度变得更大,因此即使只改变一个像素(即原始图像的三个条目)也会导致错误分类。

图 6:在 MNIST 上的不同攻击。 我们说明了由 CornerSearch ( l 0 l_{0} l0)、 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞- 和 σ \sigma σ-CornerSearch 找到的对抗样本(第二列)的差异,分别是第一、第二和第三行。第三列显示了红框突出显示区域的缩放,而第四列包含修改像素的映射(稀疏性_列)。原始图像在左上角, σ \sigma σ-map 的可视化(重新缩放使得 max i σ i = 1 \max{i}\sigma_{i}=1 maxiσi=1)在左下角。
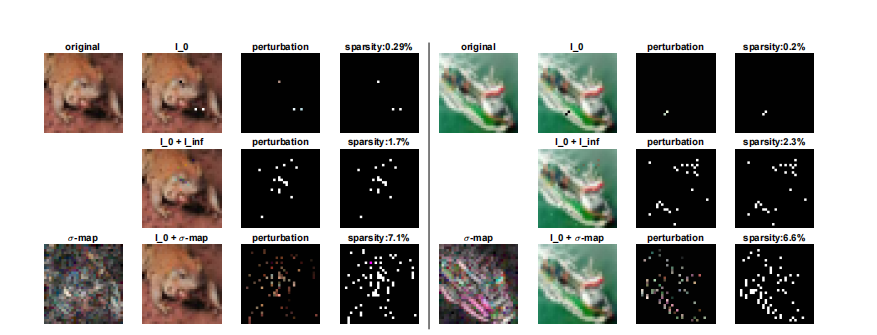
图7:CIFAR-10上的不同攻击。我们分别展示了第一、二、三行中由CornerSearch( l 0 l_0 l0)、 l 0 + l ∞ l_0 + l_\infty l0+l∞-攻击和 σ \sigma σ-CornerSearch找到的对抗样本(第二列)的差异。第三列显示了缩放到[0,1]的对抗扰动,第四列是被修改像素的映射(稀疏度列)。原始图像位于左上角,底部左侧是缩放到 max i , j σ i j = 1 \max_{i,j}\sigma_{ij}=1 maxi,jσij=1的 σ \sigma σ-映射的RGB表示。

图 8:在 Restricted ImageNet 上的不同攻击。 我们说明了由 CornerSearch ( l 0 l_{0} l0)、 l 0 + l ∞ l_{0}+l_{\infty} l0+l∞-攻击 和 σ \sigma σ-CornerSearch 找到的对抗样本(第二列,第三列放大)的差异,分别是第一、第二和第三行。第四列显示了修改像素的映射(稀疏性_列)。原始图像在左上角,重新缩放的 σ \sigma σ-map 的 RGB 表示(重新缩放使得 max i , j σ i j = 1 \max{i,j}\sigma_{ij}=1 maxi,jσij=1)在左下角。

图 9:在 MNIST 上比较 σ \sigma σ-CornerSearch 和 σ \sigma σ-PGD。 我们展示了由 σ \sigma σ-CornerSearch ( κ = 0.8 \kappa=0.8 κ=0.8)、 σ \sigma σ-PGD ( κ = 0.8 \kappa=0.8 κ=0.8) 和 σ \sigma σ-PGD ( κ = 0.6 \kappa=0.6 κ=0.6) 生成的对抗样本,以及重新缩放到 [0,1] 的各自扰动。 σ \sigma σ-PGD 使用的稀疏度级别是 k = 50 k=50 k=50。

图 10:在 CIFAR-10 上比较 σ \sigma σ-CornerSearch 和 σ \sigma σ-PGD。 我们展示了由 σ \sigma σ-CornerSearch ( κ = 0.4 \kappa=0.4 κ=0.4)、 σ \sigma σ-PGD ( κ = 0.4 \kappa=0.4 κ=0.4) 和 σ \sigma σ-PGD ( κ = 0.25 \kappa=0.25 κ=0.25) 生成的对抗样本,以及重新缩放到 [0,1] 的各自扰动。使用的稀疏度级别是 k = 100 k=100 k=100。灰色图像表示该方法未能找到对抗性操纵。
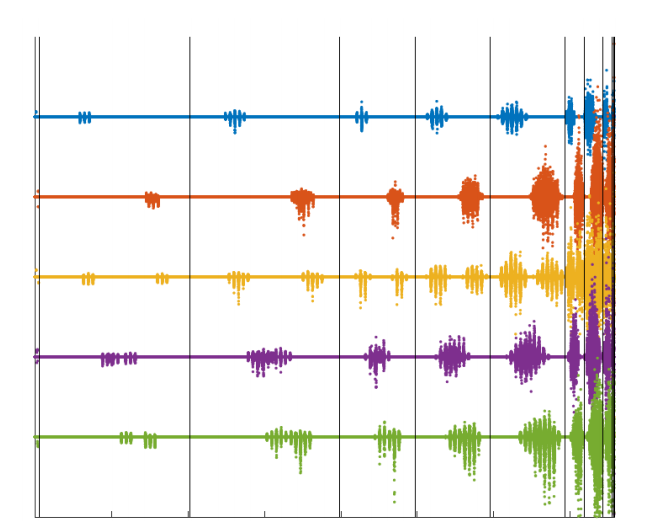
图 11:扰动的传播。 当传播测试集的图像和与之相关的对抗样本时,获得的网络每个单元值的差异。垂直线段区分不同层的单元,因此输入空间显示在左侧,输出在右侧。每种颜色代表一张图像。