这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!
**一、**用户---电影评分矩阵

在推荐系统中,最常见的任务就是预测用户对物品(这里是电影)的评分。我们通常会用一个 用户---电影评分矩阵 来表示数据:
-
行代表不同的电影
-
列代表不同的用户
-
矩阵中的值就是用户给电影的评分(比如 1 到 5 星)
在图示的例子中:
-
有 4 个用户(Alice、Bob、Carol、Dave),记作 nu=4
-
有 5 部电影(如 Love at last 、Romance forever 等),记作 nm=5
-
部分评分已知(数字),部分缺失("?"),部分用户根本没有评分(标记为 0 或空格)
关键符号
-
r(i,j)
这是一个指示函数:
-
如果用户 j 对电影 i 进行了评分,则 r(i,j)=1
-
否则 r(i,j)=0
-
-
y(i,j)
表示用户 j 对电影 i 的实际评分(如果 r(i,j)=1 才有定义)。
例如:
-
r(1,1)=1,表示 Alice 对第一部电影有评分(5 星)。
-
r(3,1)=0,表示 Alice 没有对第三部电影评分。
-
y(3,2)=4,表示 Bob 对第三部电影给了 4 星。
推荐问题的本质
从这个评分矩阵可以看出,用户对大多数电影都没有打分(即矩阵非常稀疏)。
推荐系统的任务就是:
-
根据已有评分,预测缺失的评分(图中的 "?" 位置)
-
进而为用户推荐最可能喜欢的电影
生活化解释
想象你和朋友们在一个电影打分平台上:
-
Alice 特别喜欢爱情片,她给《Love at last》和《Romance forever》都打了高分。
-
Bob 更喜欢轻松搞笑的内容,他在《Cute puppies of love》上打了 4 星。
-
Carol 和 Dave 则偏爱动作片,他们对《Nonstop car chases》和《Swords vs. karate》评分都比较高。
在这种情况下,系统会发现:
-
Alice 没有给《Cute puppies of love》打分,但因为这部电影是典型的爱情题材,而她对类似电影的评分都很高,所以系统会预测她也会喜欢,并给出一个接近 5 星的预测分。
-
同样,Dave 没有给《Swords vs. karate》打分,但因为他喜欢动作片,系统也会预测一个较高的评分。
这就是推荐系统利用 已知评分 去推测 未知评分 的过程。
**二、**为电影构建特征
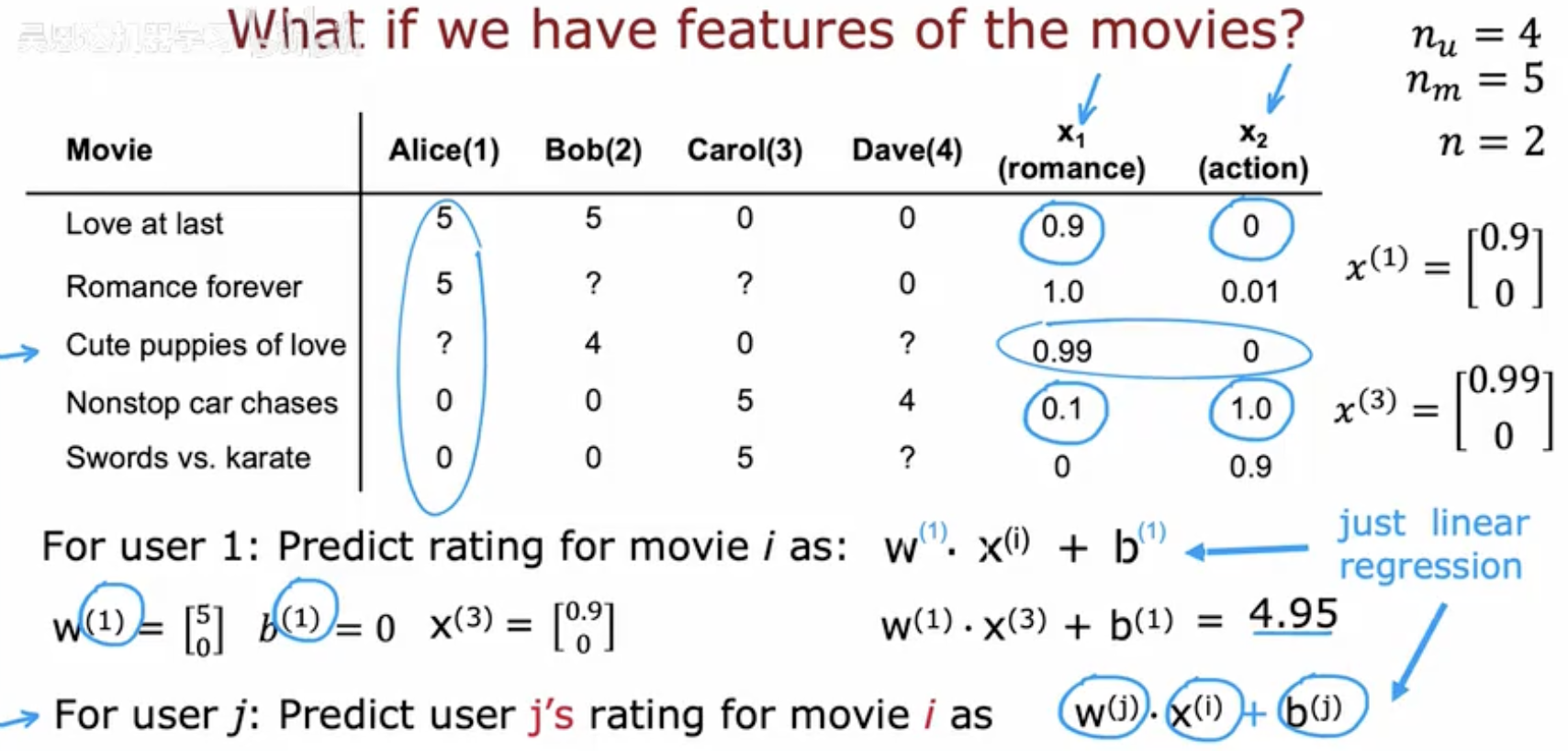
在第一节中,我们把问题描述为"补全评分矩阵",但那只是数据层面的表达。真正要让模型进行预测,就需要为每一部电影和每一个用户构建数学上的表示方式。
电影的特征向量
设每部电影都有一些可量化的特征(features),比如:
-
浪漫元素 (romance)
-
动作元素 (action)
我们可以用一个向量来表示电影的特征:
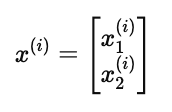
其中:
-
x1(i):电影 i 的浪漫程度(数值越高,越浪漫)
-
x2(i):电影 i 的动作程度(数值越高,越偏动作片)
例子:
-
《Love at last》是一部浪漫爱情片,可以表示为 [0.9,0]
-
《Nonstop car chases》是一部动作片,可以表示为 [0.1,1.0]
这样一来,每一部电影就从一个单纯的"名字"转化成了可计算的 特征向量。
用户的偏好向量
用户在评分时体现的是他们的兴趣偏好。我们也用一个向量来表示:
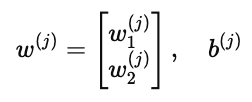
-
w(j):用户 j 对每个特征的偏好权重
-
w1(j):对浪漫元素的偏好
-
w2(j):对动作元素的偏好
-
-
b(j):用户的整体偏置,表示这个人评分普遍偏高还是偏低
预测公式
给定用户 j 和电影 i,预测评分为:
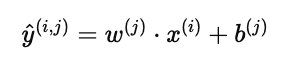
这其实就是一个 线性回归模型:
-
用户参数 w(j),b(j)
-
电影特征 x(i)
-
点积加偏置后得到预测评分
例子计算
假设:
- 用户 Alice 的参数是
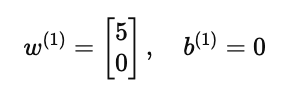
-
表示她只喜欢浪漫片,对动作片没有兴趣。
-
电影《Love at last》的特征是
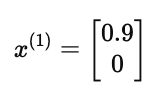
则预测分数为:
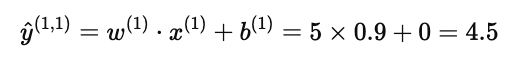
和实际评分 5 分非常接近,说明模型有效捕捉到了 Alice 的偏好。
**三、**单个用户的代价函数

在第二节中,我们建立了预测公式:
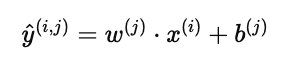
它能计算用户 j 对电影 i 的预测评分。接下来,我们需要一种方式来衡量 预测评分和真实评分之间的差距,并据此更新用户的参数 w(j),b(j)。
误差项
对用户 j 而言,我们只在他/她已经打过分的电影上比较预测和实际:
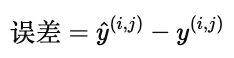
-
如果预测值接近真实评分,误差就小。
-
如果预测值差距很大,误差就大。
均方误差 (MSE)
为了整体衡量用户 j 的预测准确性,我们采用均方误差:
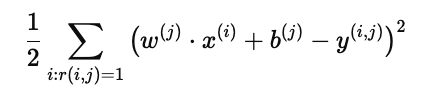
解释:
-
求和范围:仅在用户 j 确实打分过的电影 (r(i,j)=1) 上计算。
-
平方:让误差为正,且惩罚偏差较大的预测。
-
1/2 系数:为了在后续求导时简化公式。
正则化项
如果只最小化均方误差,可能会导致 w(j) 参数过大,造成过拟合。
因此我们引入 L2 正则化:
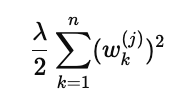
解释:
-
约束每个用户的参数规模,避免"过度依赖"某个特征。
-
λ 控制正则化强度:
-
λ 大 → 参数更小,更保守
-
λ 小 → 参数更自由,但风险更大
-
单用户的完整代价函数
综合上述两部分:
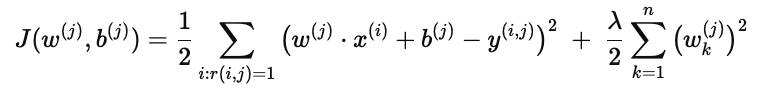
含义:
-
第一部分 → 确保预测尽可能接近用户 j 的真实评分
-
第二部分 → 控制参数规模,提升泛化能力
直观理解
-
对 Alice 而言,代价函数的目标是:找到一组参数 w(1),b(1),能最好地拟合她对所有已看过电影的评分。
-
这就像是在问:"怎样描述 Alice 的口味,才能既符合她看过的电影评分,又不会把她的偏好夸大到极端?"
**四、**所有用户的联合优化

在第三节中,我们针对 单个用户 jj 定义了代价函数,用来学习他的偏好参数 w(j),b(j)。
但在实际的推荐系统中,我们面对的是成千上万的用户,因此需要一个 全局的代价函数,同时学习所有用户的参数。
全局代价函数
综合所有用户:
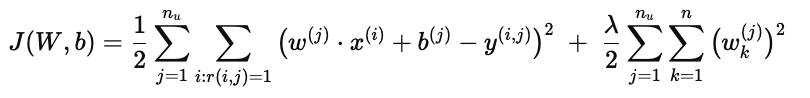
解释:
-
第一项:
-
遍历 所有用户,并对他们打过分的电影计算预测误差。
-
目标是让整个系统的预测都尽量准确。
-
-
第二项:
-
对所有用户的参数 w(j) 加上正则化约束。
-
避免某些用户参数过大,保证整体模型的稳定性。
-
参数优化的目标
我们最终希望学到:
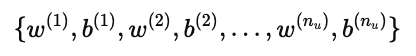
也就是说,每个用户都得到一个 个性化的参数向量和偏置,用于捕捉他的兴趣偏好。
意义与优势
-
统一建模
-
所有用户的学习目标整合进同一个代价函数。
-
这样可以保证用户之间共享同一组电影特征向量 x(i),增强模型的连贯性。
-
-
提升泛化
-
如果某个用户的评分数据较少,模型仍可以通过其他用户的学习结果间接获益。
-
这有助于缓解数据稀疏问题。
-
-
更精准的推荐
- 优化后,每个用户都拥有专属的参数,能更好地预测缺失评分,从而推荐更符合其兴趣的电影。
举个例子
假设系统中有 1000 个用户:
-
对于喜欢浪漫片的用户们,参数 w(j) 会自动学习到对 romance 特征 的权重较高。
-
对于喜欢动作片的用户们,参数会学习到对 action 特征 的权重更大。
-
对于混合型口味的用户,系统则能平衡这两种特征。
通过这种方式,推荐系统就能为不同兴趣的群体生成定制化预测。
这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!