在这个汇总中整理了 插入,希尔,选择,快排,堆排,冒泡,归并
还有非比较排序 计数,基数排序
算法的稳定性:再对相同值的元素排序之后,如果元素之间的顺序并没有发生变化,则是稳定的
对一个数组向前表示下标减减 向后加加
插入排序
性质:稳定 时间复杂度 O(N^2)
原理
选择一个元素 v 为基准,假定 v 前面的元素时有序的,那么就可以把 v 和 v 下标 -1 的 p 元素向前进行对比,如果比 v 大那么就覆盖 v 的位置,继续往前比较,当p 小于或者等于 v 时那么就可以退出这一次循环了,因为p 下标 +1 就对应了v应该插入的位置,于是把这个下标值改为 v ,这一次循环就对 v 进行了一次排序 再对整个数组元素进行排序,就完成了最终的排序
java
public static void InsertSort(int[] array) {
//默认j前面的数是有序的
for (int j = 1; j < array.length; j++) {
int tmp = array[j];
int i = j - 1;
for (; i >= 0; i--) {
if (array[i] > tmp) {
array[i + 1] = array[i];
} else {
// array[i + 1] = tmp;
break;
}
}
array[i + 1] = tmp;
}
}希尔排序
不稳定 O(N^1.3)~O(N^1.5)
和插入排序的排序逻辑是相同的,但是他引入增量gap的概念,通过将数组分为gap个组,在对这些组进行插入排序,这样元素就不是一位一位的移动了,能使较大的元素快速的移动到后面,再不断的缩小gap的值,最终在gap等于1时就和插入排序一样了,但是这时的数组已经趋于有序了
java
public static void shellSort(int[] array) {
int gap = array.length;//增量
while (gap > 1) {
gap /= 2;
InsertSortByShell(array, gap);
}
}
private static void InsertSortByShell(int[] array, int gap) {
//默认j前面的数是有序的
for (int j = gap; j < array.length; j++) {
int tmp = array[j];
int i = j - gap;
for (; i >= 0; i -= gap) {
if (array[i] > tmp) {
array[i + gap] = array[i];
} else {
break;
}
}
array[i + gap] = tmp;
}
}选择排序
不稳定 O(N^2)
通过遍历数组来找到最小的元素,在把他和第一位的下标交换,这样一次循环就对一个元素完成了排序,在对整个数组进行排序,最终使得数组有序
优化 可以在遍历时找到最大的元素,这样一次遍历能完成俩个元素的排序
java
public static void selectSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
int minIndex = i;
for (int j = i; j <= array.length - 1; j++) {
if (array[minIndex] > array[j]) {
minIndex = j;
}
}
swap(array, minIndex, i);
}
}
public static void selectSort_better(int[] array) {
int i = 0;
int k = array.length - 1;
while(i <= k){
int minIndex = i;
int maxIndex = i;
for (int j = i; j <= array.length - 1 - i; j++) {
if (array[minIndex] > array[j]) {
minIndex = j;
}
if (array[maxIndex] < array[j]) {
minIndex = j;
}
}
swap(array, minIndex, i);
if (maxIndex == i) {
maxIndex = minIndex;
}
swap(array, maxIndex, k);
i++;k--;
}
}快速排序
不稳定 O(Nlog(N))
快速排序是hoare提出的一种基于二叉树结构的排序算法,通过指定一个待排元素,以他为中心将数组分为俩部分,左边值全是小于该元素,右边值全是大于该元素,然后以这个元素最终的下标,继续向左右俩部分进行排序,最终走到左右部分长度为0 (left == right) 时完成排序
排序主逻辑
java
public static void quickSort(int[] array) {
quickSortMain(array,0,array.length - 1);
}
private static void quickSortMain(int[] array, int left, int right) {
if (right <= left) {
return;
}
//优化
// 1 三数取中 保证不会递归很深导致栈溢出
// getMiddle(array,left,right);
// 2 递归到小区间时使用插入排序
if (right - left < 7) {
InsertSort(array, left, right);
return;
}
//以array[left]为基准,吧数组分开 放回中点的下标
int middle = separate_hoare(array, left, right);
//递归
//左边
quickSortMain(array, left, middle - 1);
//右边
quickSortMain(array, middle + 1, right);
}将数组分割成左右俩部分常见的方法有
hoare版
指定left下标为基准值,使用i j 代表左右下标,i j 分别表示的时 在小于 i 下标的所有元素都小于等于基准值 大于 j 下标的所有元素都大于等于基准值
java
private static int separate_hoare(int[] array, int left, int right) {
int pivot = array[left];
int tmp = left;
while (right != left) {
//从右边找到比pivot小的数
while (right > left && array[right] >= pivot) {
right--;
}
//从左边找到比pivot大的数
while (right > left && array[left] <= pivot) {
left++;
}
swap(array, left, right);
}
swap(array, tmp, left);
return left;
}挖坑法
将基准值储存起来,在找到合适的元素时,直接将这个值给覆盖到对应的位置,这样可以少去交换的逻辑
java
//挖坑法 将pivot储存在tmp中,直接吧值覆盖在原数据上
private static int separate_dig(int[] array, int left, int right) {
int pivot = array[left];
while (left != right) {
//走右边
while (left < right && array[right] >= pivot) {
right--;
}
//直接填入
array[left] = array[right];
//左边
while (left < right && array[left] <= pivot) {
left++;
}
array[right] = array[left];
}
array[left] = pivot;
return left;
}双指针法
使用双指针一次遍历完成数组的分割,让 i 来完后找比pivot小的值,然后d代表的时d前面的全是小于或等于piovt的值,在和d交换d++,那么d也就维护了一个(0,d-1)这个区间全是小于或等于pivot,最终和 left 一交换,就完成了数组的分割
java
//双指针法
private static int separate_index(int[] array, int left, int right) {
int d = left + 1;
int pivot = array[left];
for (int i = left + 1; i <= right; i++) {
if (array[i] < pivot) {
swap(array, i, d);
d++;
}
}
swap(array, d - 1, left);
return d - 1;
}优化
三数取中防止递归太深
将左边中间右边做对比,取中间值来作为基准值
java
private static void getMiddle(int[] array, int left, int right) {
int middle = (left + right) / 2;
if (array[left] < array[middle] && array[middle] < array[right]//取m
|| array[right] < array[middle] && array[middle] < array[left]) {
swap(array,left, middle);
} else if (array[middle] < array[right] && array[middle] < array[left]//去right
|| array[left] < array[middle] && array[right] < array[middle]) {
swap(array, left, right);
} else {
return;
}
}堆排序
时间复杂都 O(N*logN) 空间复杂度 O(1) 不稳定
堆排序基于大小根堆的性质,因为小根堆有堆顶元素时是数组中最小的元素的性质,那么就可以基于大根堆的shiftdwon来进行原地升序排序,shiftdwon向下调整使用从数组末尾开始对元素进行向下调整,这样这个开始位置最终就是相对的最大元素,等到走到数组头位置,那么就完成了最大元素的寻找
* shiftdwon实现,因为有左节点 child = parent * 2 + 1 右节点 child = parent * 2 + 2, 那么从开始位置记为根节点,与他的左右节点比较,最终和最大的节点交换,然后根节点走到这个子节点,并继续向下交换,当节点下标超过了数组长度,就完成了一次向下调整
java
public static void heapSort(int[] array) {
int useSize = array.length;//这个是下表的最后元素
while (useSize > 0) {
creatHeap(array,useSize);//创建大根堆,创建一次找到一个最大值
swap(array, 0, useSize-1);//这个是最后元素的下表
useSize--;
}
}
public static void creatHeap(int[] array,int userSize) {
for (int i = array.length - 1; i >= 0; i--) {//每个元素都要遍历
shiftDown(array,i, userSize);
}
}
private static void shiftDown(int[] array,int parent, int userSize) {
int child = parent * 2 + 1;//这个是父节点的左节点
while (child < userSize) {
//和大的交换
if ((child+1) < userSize && array[child] < array[child + 1]) {
child++;//走到更大的右节点
}
if (array[child] > array[parent]) {//交换
swap(array, child, parent);
parent = child;
child = child*2+1;//走到写一个左节点
}else {//说明调整好了
break;
}
}
}冒泡排序
O(n^2) 稳定
通过俩次嵌套循环来完成排序,里面的一次完成一个元素的排序,这样外层循环遍历一次数组就完成排序
java
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length; i++) {
boolean flg = true;
for (int j = i+1; j < array.length; j++) {
if (array[j] < array[i]) {
swap(array, j, i);
flg = false;
}
}
if (flg) {
return;
}
}
}归并排序
O(Nlog(N)) O(N) 稳定
归并排序主逻辑分为递归和合并俩部分,递归把所有的元素按中间分为俩部分,一直分到数组的叶子节点,在向上回溯,并将左右俩个数组有序合并在一起,这里不用关心左右俩数组是否有序,是因为我时从俩个元素开始合并的,得到的也是有序数组,那么在向上到多个元素也会是有序的,左边俩个元素有序,右边俩个元素也肯定是有序的,最后把这个合并的有序的数组段给覆盖到原来数组的那一段,就完成这一段的排序了
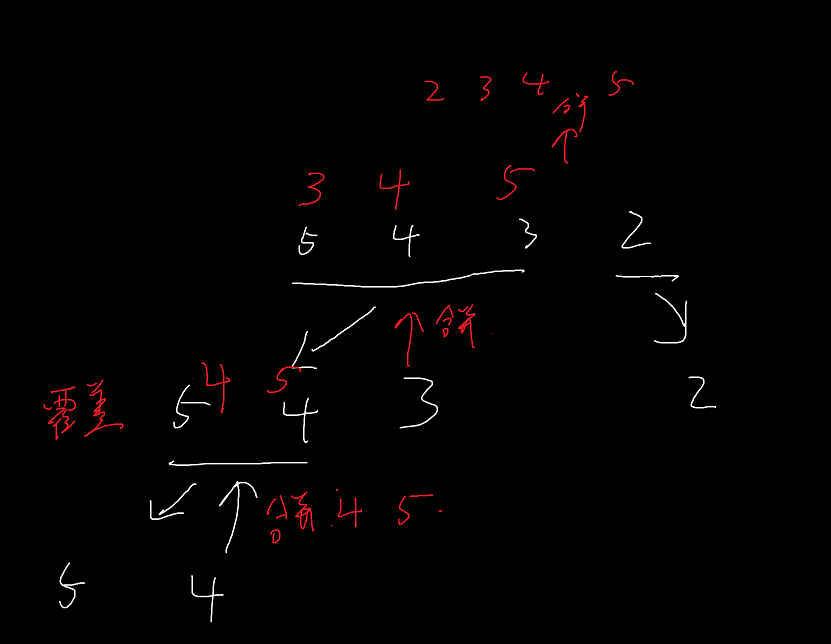
java
public static void mergeSort(int[] array) {mergeSortMain(array,0,array.length-1);}
private static void mergeSortMain(int[] array, int left, int right) {
if (left >= right) {
return;
}
int middle = (right + left) / 2;
//递归 吧数递归为单独的数
mergeSortMain(array, left, middle);//左
mergeSortMain(array, middle+1, right);//右
//合并
merge(array,middle, left, right);
}
//创建一个新的数组,再把新的数组的数拷贝到老的数组
private static void merge(int[] array, int middle, int left, int right) {
int[] newArray = new int[right - left + 1];
int i = 0;
//左边的数组
int s1 = left;
int e1 = middle;
//右边的数组
int s2 = middle + 1;
int e2 = right;
//排序
while (s1 <= e1 && s2 <= e2) {
if (array[s1] < array[s2]) {
newArray[i++] = array[s1];
s1++;
} else {
newArray[i++] = array[s2];
s2++;
}
}
while (s1 <= e1) {//s1没有拍完
newArray[i++] = array[s1++];
}
while (s2 <= e2) {//s2没有拍完
newArray[i++] = array[s2++];
}
//将数组拷贝到老数组
i = 0;
for (int j = left; j <= right; j++) {
array[j] = newArray[i++];
}
}计数排序
O(N + K) O(N + K) 不稳定
N是数组长度 K是数据大小范围
计数排序是非排序的算法,通过遍历一次数组并记下所有元素出现的频率,在从小到大把记下的元素给覆盖到原数组中,就完成了排序
public static void countSort(int[] array) {
int min = array[0];
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] < min) {
min = array[i];
}
if (array[i] > max) {
max = array[i];
}
}
countSortMain(array,min,max);
}
public static void countSortMain(int[] array, int min, int max) {
int[] newArray = new int[max - min + 1];
//遍历array
for (int j : array) {
newArray[j - min]++;
}
//拷贝
int i = 0;
for (int j = 0 ; j < array.length;j++) {
while (newArray[j] > 0) {
// System.out.print((j + min) + " ");
array[i++] = j + min;
newArray[j]--;
}
}
}基数排序
O(N * K) N 元素个数 K最大数的位数
基数排序也是非排序的算法,使用10个队列来储存数字的 0-9 位数,先获取到元素的个位数,并储存在对应的队列中,一次遍历数组,在队列从0-9把储存的元素覆盖给数组,就完成了个位的排序,在排十位数,百位数,直到最大位数所有位都每排过了
java
public static void oddSort(int[] array) {
//创建10个队列
Queue<Integer>[] queues = new Queue[10];
for (int i = 0; i < 10; i++) {
queues[i] = new LinkedList<Integer>();
}
//找到最大的数
int max = array[1];
for (int i = 1; i < array.length; i++) {
max = Math.max(max, array[i]);
}
int times = 0;//决定这次循环比较的是哪位数
while (max != 0) {
for (int i = 0; i < array.length; i++) {//遍历则这个数组
int tmpVal = array[i];
for (int j = 0; j < times; j++) {//决定比较哪位数
tmpVal /= 10;
}
int index = tmpVal % 10;//根据该为数来选择插入哪个队列
queues[index].add(array[i]);
}
//重新为这个数组排序
int indexArr = 0;
for (Queue<Integer> tmp : queues) {
while (!tmp.isEmpty()) {
array[indexArr++] = tmp.poll();
}
}
times++;
max /= 10;
}
}