目录
[1. 图像渲染](#1. 图像渲染)
[1.1 题目解析](#1.1 题目解析)
[1.2 解法](#1.2 解法)
[1.3 代码实现](#1.3 代码实现)
[2. 岛屿数量](#2. 岛屿数量)
[2.1 题目解析](#2.1 题目解析)
[2.2 解法](#2.2 解法)
[2.3 代码实现](#2.3 代码实现)
1. 图像渲染
https://leetcode.cn/problems/flood-fill/description/
有一幅以 m x n 的二维整数数组表示的图画 image ,其中 image[i][j] 表示该图画的像素值大小。你也被给予三个整数 sr , sc 和 color 。你应该从像素 image[sr][sc] 开始对图像进行上色 填充 。
为了完成 上色工作:
- 从初始像素开始,将其颜色改为
color。 - 对初始坐标的 上下左右四个方向上 相邻且与初始像素的原始颜色同色的像素点执行相同操作。
- 通过检查与初始像素的原始颜色相同的相邻像素并修改其颜色来继续 重复 此过程。
- 当 没有 其它原始颜色的相邻像素时 停止 操作。
最后返回经过上色渲染 修改 后的图像 。
示例 1:
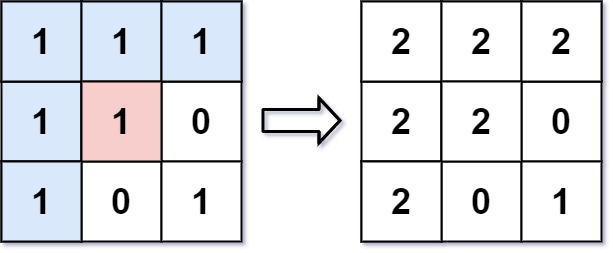
**输入:**image = [[1,1,1],[1,1,0],[1,0,1]],sr = 1, sc = 1, color = 2
输出:[[2,2,2],[2,2,0],[2,0,1]]
解释: 在图像的正中间,坐标 (sr,sc)=(1,1) (即红色像素),在路径上所有符合条件的像素点的颜色都被更改成相同的新颜色(即蓝色像素)。
注意,右下角的像素 没有 更改为2,因为它不是在上下左右四个方向上与初始点相连的像素点。
1.1 题目解析
题目本质
从指定起点开始,对二维网格中所有连通的相同颜色区域进行重新着色,这是一个典型的"连通区域遍历"问题。
常规解法
最直观的想法是使用深度优先搜索(DFS)或广度优先搜索(BFS),从起始点开始向四个方向扩散,将所有与起始点颜色相同且连通的像素点都改为新颜色。
问题分析
直观解法本身是正确的,关键在于实现细节。需要注意边界检查、避免重复访问、以及特殊情况处理(如新颜色与原颜色相同)。时间复杂度为O(m×n),空间复杂度为O(m×n)(递归栈深度)。
思路转折
要想正确实现 → 必须处理好递归边界 → 记录原始颜色并在递归中判断。同时要避免不必要的操作,如果新颜色与原颜色相同则直接返回。
1.2 解法
算法思想:
- 使用深度优先搜索(DFS)进行连通区域遍历
- 递推关系:dfs(x,y) = 改变当前点颜色 + dfs(四个相邻点)
- 终止条件:越界或颜色不匹配
**i)**记录起始点的原始颜色,如果与目标颜色相同则直接返回
**ii)**获取图像的行数和列数用于边界检查
**iii)**从起始点开始执行DFS
**iv)**在DFS中,先将当前点改为新颜色
**v)**遍历四个方向,对满足条件的相邻点递归调用DFS
**vi)**满足条件:不越界且颜色与原始颜色相同
易错点:
-
**变量作用域问题:**成员变量m,n必须正确赋值,不能被局部变量遮蔽
-
**边界检查顺序:**必须先检查越界再检查颜色,避免数组越界
-
**颜色判断:**递归时要与原始颜色比较,不是与新颜色比较
-
**特殊情况:**新颜色与原颜色相同时要提前返回,避免无限递归
1.3 代码实现
java
class Solution {
int[] dx = {0, 0, 1, -1}; // 四个方向:右、左、下、上
int[] dy = {1, -1, 0, 0};
int m, n; // 图像尺寸
int originalColor; // 原始颜色
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
originalColor = image[sr][sc];
// 如果新颜色与原颜色相同,直接返回避免无限递归
if (originalColor == color) return image;
m = image.length;
n = image[0].length;
dfs(image, sr, sc, color);
return image;
}
private void dfs(int[][] image, int row, int col, int newColor) {
// 将当前像素改为新颜色
image[row][col] = newColor;
// 遍历四个方向
for (int i = 0; i < 4; i++) {
int newRow = row + dx[i];
int newCol = col + dy[i];
// 边界检查 + 颜色检查
if (newRow >= 0 && newRow < m &&
newCol >= 0 && newCol < n &&
image[newRow][newCol] == originalColor) {
dfs(image, newRow, newCol, newColor);
}
}
}
}复杂度分析
- 时间复杂度:O(m×n),最坏情况下需要访问图像中的每个像素点一次
- 空间复杂度:O(m×n),递归调用栈的最大深度,最坏情况下(如蛇形连通区域)可能达到m×n
2. 岛屿数量
https://leetcode.cn/problems/number-of-islands/description/
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
['1','1','1','1','0'],
['1','1','0','1','0'],
['1','1','0','0','0'],
['0','0','0','0','0']
]
输出:1示例 2:
输入:grid = [
['1','1','0','0','0'],
['1','1','0','0','0'],
['0','0','1','0','0'],
['0','0','0','1','1']
]
输出:3提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
2.1 题目解析
题目本质
在二维网格中统计连通分量的个数,这是一个典型的"连通区域计数"问题。每个由'1'组成的连通区域代表一个岛屿。
常规解法
最直观的想法是遍历整个网格,每当遇到一个未访问的'1'时,就从这个点开始进行深度优先搜索(DFS)或广度优先搜索(BFS),将整个连通的岛屿标记为已访问,同时岛屿计数加1。
问题分析
直观解法是正确且高效的。关键在于避免重复计算同一个岛屿,需要使用访问标记数组。时间复杂度为O(m×n),因为每个格子最多被访问一次;空间复杂度为O(m×n),用于存储访问标记和递归栈。
思路转折
要想正确统计 → 必须避免重复计数 → 使用访问标记数组。每次发现新的未访问陆地时,就找到了一个新岛屿,然后通过DFS将整个岛屿标记为已访问,确保不会重复计算。
2.2 解法
算法思想:
- 使用深度优先搜索(DFS) + 访问标记进行连通分量计数
- 递推关系:dfs(x,y) = 标记当前点 + dfs(四个相邻的陆地点)
- 计数策略:每次DFS调用代表发现一个新岛屿
**i)**初始化访问标记数组和岛屿计数器
**ii)**双重循环遍历整个网格
**iii)**当遇到未访问的陆地('1')时,岛屿计数加1
**iv)**从该点开始DFS,将整个连通的岛屿标记为已访问
**v)**在DFS中,标记当前点为已访问,然后递归访问四个方向的相邻陆地
**vi)**返回最终的岛屿计数
易错点:
-
**重复标记:**在DFS入口和递归调用前都标记,导致代码冗余
-
**边界检查顺序:**应该先检查越界,再检查访问状态和格子值
-
**数据类型:**网格元素是字符'1'和'0',不是数字1和0
2.3 代码实现
java
class Solution {
int[] dx = {0, 0, 1, -1}; // 四个方向:右、左、下、上
int[] dy = {1, -1, 0, 0};
int m, n;
boolean[][] visited;
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) return 0;
m = grid.length;
n = grid[0].length;
visited = new boolean[m][n];
int islandCount = 0;
// 遍历整个网格
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 发现未访问的陆地,开始新的岛屿探索
if (grid[i][j] == '1' && !visited[i][j]) {
dfs(grid, i, j);
islandCount++; // 完成一个岛屿的探索,计数加1
}
}
}
return islandCount;
}
private void dfs(char[][] grid, int row, int col) {
// 标记当前位置为已访问
visited[row][col] = true;
// 探索四个方向
for (int i = 0; i < 4; i++) {
int newRow = row + dx[i];
int newCol = col + dy[i];
// 边界检查 + 访问检查 + 陆地检查
if (newRow >= 0 && newRow < m &&
newCol >= 0 && newCol < n &&
!visited[newRow][newCol] &&
grid[newRow][newCol] == '1') {
dfs(grid, newRow, newCol);
}
}
}
}复杂度分析
- 时间复杂度:O(m×n),每个网格单元最多被访问一次,遍历整个网格需要O(m×n)时间
- 空间复杂度:O(m×n),需要O(m×n)的访问标记数组,递归调用栈在最坏情况下(整个网格都是陆地且呈蛇形)深度可达O(m×n)