目录
[No.1 回文子串](#No.1 回文子串)
[No.2 最长回文子串](#No.2 最长回文子串)
[No.3 分隔回文串IV](#No.3 分隔回文串IV)
[No.4 分割回文串II](#No.4 分割回文串II)
[No.5 最长回文子序列](#No.5 最长回文子序列)
[No.6 让字符串成为回文串的最少插入次数](#No.6 让字符串成为回文串的最少插入次数)
No.1 回文子串
题目描述:
具有不同开始位置或者结束位置的子串,即使是由相同字符组成,也视作不同的回文子串。
子串也要求连续性。
返回回文子串数量。

思路:
ps:可以用更优的 中心扩展算法 or 马拉车算法 来解决这道题。这里只介绍动规。
我们可以通过dp,以n方级别复杂度将所有的子串是否回文的信息,保存在dp表里面。
创建二维dp表,i表示起始位置,j从i开始往后遍历。

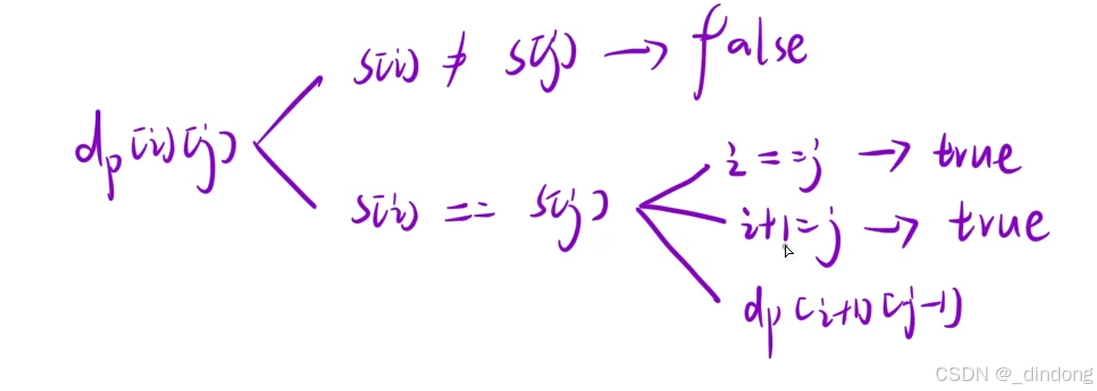
s[i]==s[j]后的细分判断顺序很好的避免了越界
回文串的填表顺序有点不同,二维表的填表顺序应该是从下往上因为dp[i][j]需要考虑dp[i+1][j-1]
最后返回dp表里true的个数。完美解决。
cpp
class Solution {
public:
int countSubstrings(string s) {
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
int ret = 0;
for (int i = n - 1; i >= 0; --i) {
for (int j = i; j < n; ++j) {
if (s[i] == s[j])
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
if (dp[i][j])
++ret;
}
}
return ret;
}
};No.2 最长回文子串

思路和上一题一致,填表过程中更新最长回文子串的起始位置和大小
cpp
class Solution {
public:
string longestPalindrome(string s) {
int n=s.size(),len=0,begin=0;
vector<vector<bool>> dp(n,vector<bool>(n));
for(int i=n-1;i>=0;--i)
{
for(int j=i;j<n;++j)
{
if(s[i]==s[j])dp[i][j]=i+1<j?dp[i+1][j-1]:true;
if(dp[i][j]&&len<j-i+1)
{
len=j-i+1;begin=i;
}
}
}
return s.substr(begin,len);
}
};No.3 分隔回文串IV

思路:
暴力:将字符串分成三个部分的所有情况都枚举,判断有没有全都是回文的。
转成dp也很好想
cpp
class Solution {
public:
bool checkPartitioning(string s) {
int n=s.size();
vector<vector<bool>> dp(n,vector<bool>(n));
for(int i=n-1;i>=0;--i)
{
for(int j=i;j<n;++j)
{
if(s[i]==s[j])dp[i][j]=i+1<j?dp[i+1][j-1]:true;
}
}
for(int i=1;i<n-1;++i)
{
for(int j=i;j<n-1;++j)
{
if(dp[0][i-1]&&dp[i][j]&&dp[j+1][n-1])return true;
}
}
return false;
}
};No.4 分割回文串II

思路:
既然已经知道我们可以通过dp表将任何区间的回文情况存好,那么这题就相当于在问,将原数组分成区间,让区间都是true的同时数量最少。无非就是判断区间内能不能符合子串,有点类似单词划分那题。

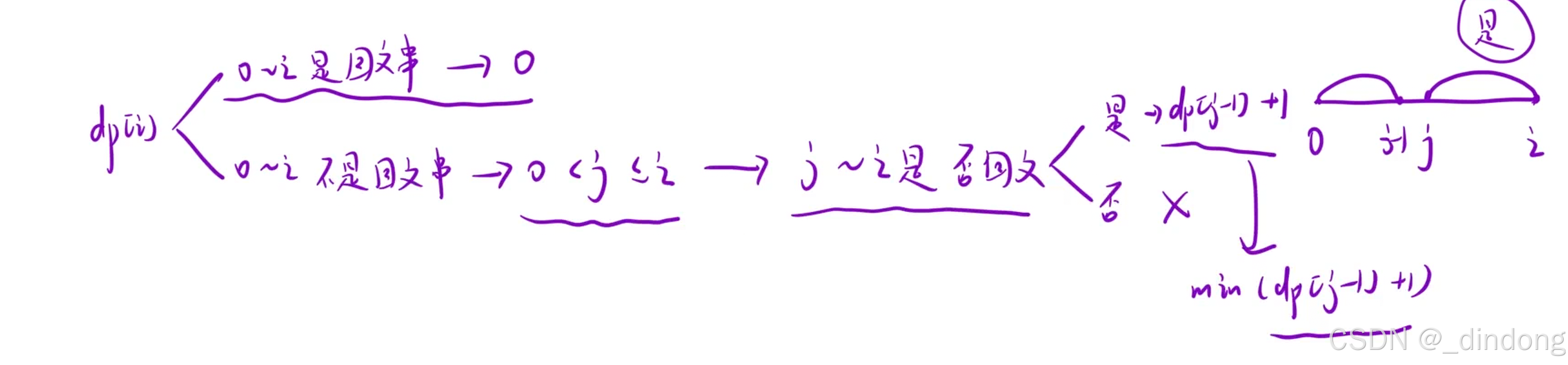
因为要求min,初始化所有值为INT_MAX
cpp
class Solution {
public:
int minCut(string s) {
int n=s.size();
vector<vector<bool>> isPal(n,vector<bool>(n));
for(int i=n-1;i>=0;--i)
{
for(int j=i;j<n;++j)
{
if(s[i]==s[j])isPal[i][j]=i+1<j?isPal[i+1][j-1]:true;
}
}
vector<int> dp(n,INT_MAX);
for(int i=0;i<n;++i)
{
if(isPal[0][i])dp[i]=0;
else
{
for(int j=1;j<=i;++j)
{
if(isPal[j][i])dp[i]=min(dp[i],dp[j-1]+1);
}
}
}
return dp[n-1];
}
};No.5 最长回文子序列

子序列,和前面的子串不一样了。
回文:二维表存储?i~j存储回文信息?和之前不一样,子序列不要求连续。那么这里我们选择dp[i][j]表示i~j内部最长子序列长度。回文判断:每次往两边扩展。
子序列:二维表[i][j]表示i~j区间内的最长回文子序列长度

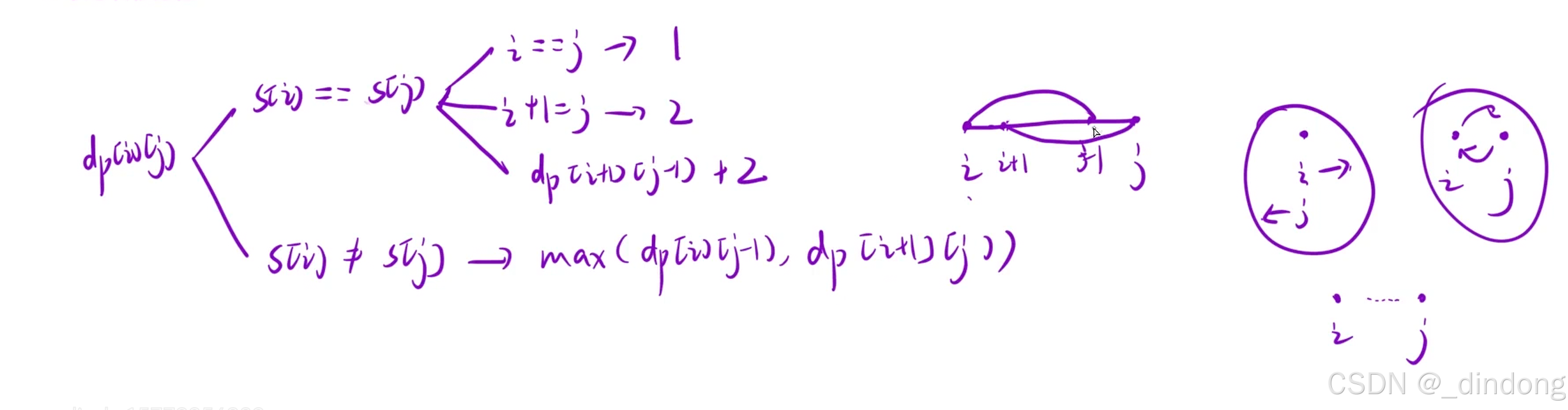
填表顺序从下到上,从左到右
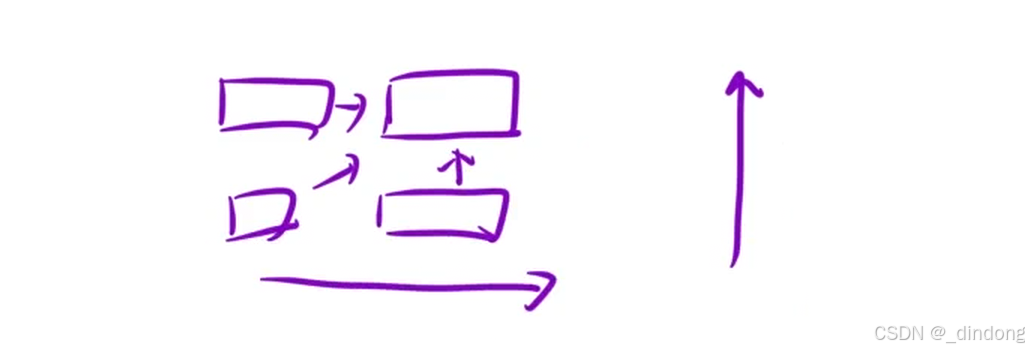
初始化将主对角上的值设置为1,因为dp值表示区间内最大子序列长度
cpp
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n=s.size();
vector<vector<int>> dp(n,vector<int>(n));
for(int i=n-1;i>=0;--i)
{
//i==j
dp[i][i]=1;
//从i+1开始遍历,融合相等的另外两种分支
for(int j=i+1;j<n;++j)
{
if(s[i]==s[j])dp[i][j]=dp[i+1][j-1]+2;
else dp[i][j]=max(dp[i+1][j],dp[i][j-1]);
}
}
return dp[0][n-1];
}
};No.6 让字符串成为回文串的最少插入次数
1312. 让字符串成为回文串的最少插入次数 - 力扣(LeetCode)

需要二维表分区间讨论

不等时,分别向左右讨论
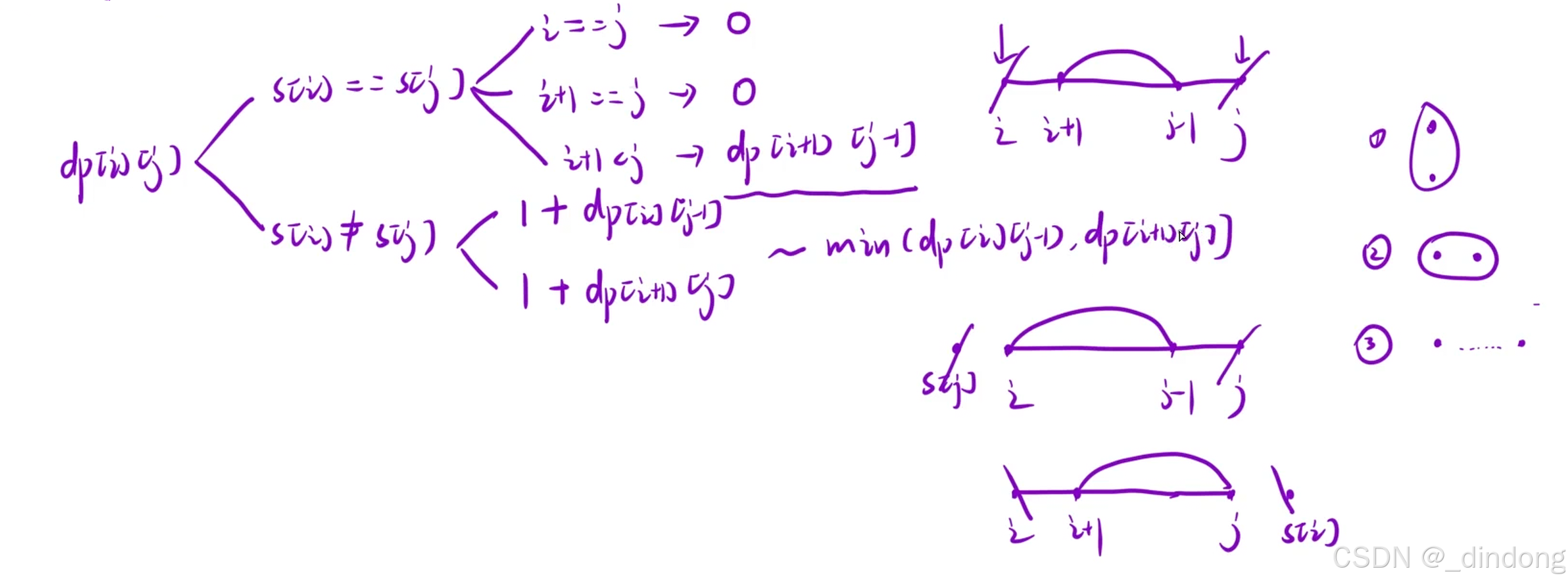
cpp
class Solution {
public:
int minInsertions(string s) {
int n=s.size();
vector<vector<int>> dp(n,vector<int>(n));
for(int i=n-1;i>=0;--i)
{
for(int j=i+1;j<n;++j)
{
if(s[i]==s[j])dp[i][j]=dp[i+1][j-1];
else dp[i][j]=1+min(dp[i][j-1],dp[i+1][j]);
}
}
return dp[0][n-1];
}
};回文串的问题可以转换成区间讨论的问题,这有利于我们确定最重要的状态表示。( •̀ ω •́ )✧
此篇完。