原文链接:https://arxiv.org/pdf/2411.14716
本文提出VisionPAD,一种自监督的预训练范式,用于自动驾驶中的视觉算法。
1. 概述
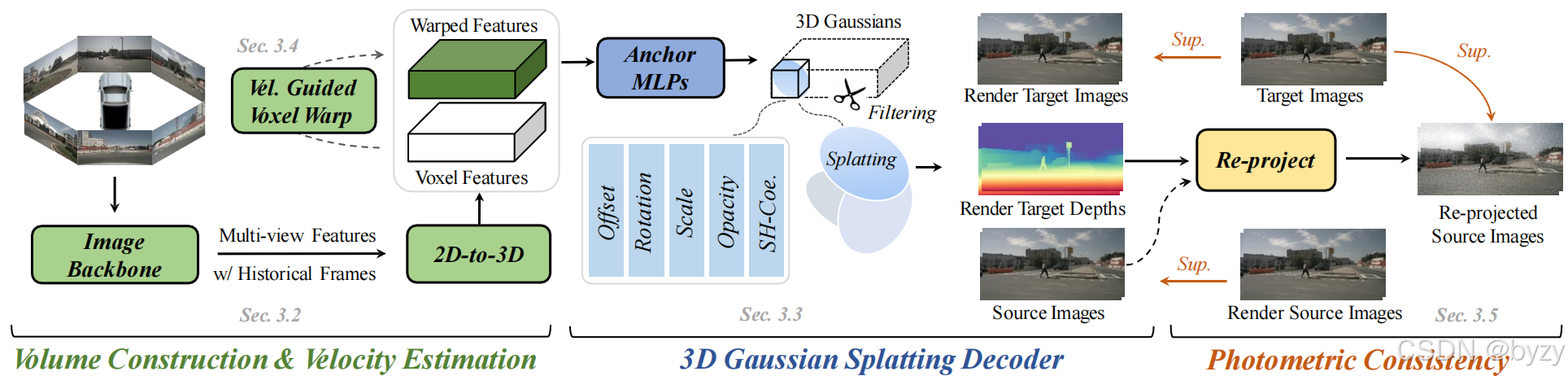
如图所示,VisionPAD包含4个关键模块:
- 输入历史的多帧多视图图像,使用带显式表达(即占用)的视觉感知主干网络。
- 使用3D高斯溅射解码器从体素表达中重建当前帧的多视图图像。
- 预测体素速度,从而可将当前帧体素特征变形到目标帧。这有助于使用3DGS解码器重建多视图相邻帧图像和深度图。
- 使用当前帧的目标深度图,通过光度一致性损失引入3D几何约束。
2. 体素建立
- 使用共享的图像主干 ,从 M M M帧历史的 N N N视图图像 I = { I i } i = 1 M I=\{I_i\}_{i=1}^M I={Ii}i=1M中提取2D图像特征 F I ∈ R N × H × W × C F_I\in\mathbb R^{N\times H\times W\times C} FI∈RN×H×W×C。
- 使用视图变换提升到以自车为中心的3D坐标系,生成体素特征。
- 使用由卷积组成的投影层 细化表达,得到 V ∈ R X × Y × Z × C V\in\mathbb R^{X\times Y\times Z\times C} V∈RX×Y×Z×C。
3. 3D高斯溅射解码器
3.1 准备知识
3D高斯溅射将3D场景表达为一组高斯基元 { g k = ( μ k , Σ k , α k , c k ) } k = 1 K \{g_k=(\mu_k,\Sigma_k,\alpha_k,c_k)\}_{k=1}^K {gk=(μk,Σk,αk,ck)}k=1K,其中每个高斯 g k g_k gk通过均值 μ k ∈ R 3 \mu_k\in R^3 μk∈R3,协方差 Σ k \Sigma_k Σk,不透明度 α k ∈ [ 0 , 1 ] \alpha_k\in[0,1] αk∈[0,1]以及球面谐波系数(SH) c k ∈ R k c_k\in R^k ck∈Rk表达。
协方差 Σ \Sigma Σ被参数化为缩放矩阵 S ∈ R + 3 S\in\mathbb R^3_+ S∈R+3和旋转矩阵 R ∈ R 4 R\in\mathbb R^4 R∈R4:
Σ = R S S T R T \Sigma=RSS^TR^T Σ=RSSTRT
将3D高斯投影到2D图像平面需要使用视图变换 W W W和投影变换仿射近似的雅可比矩阵 J J J。可根据下式得到投影的2D协方差 Σ ′ \Sigma' Σ′:
Σ ′ = J W Σ W T J T \Sigma'=JW\Sigma W^TJ^T Σ′=JWΣWTJT
为进行给定视角下的图像渲染,每个像素 p p p的特征通过混合 K K K个有序的高斯得到,即alpha混合:
C ( p ) = ∑ i = 1 K c i α i ∏ j = 1 i − 1 ( 1 − α j ) C(p)=\sum_{i=1}^{K}c_i\alpha_i\prod_{j=1}^{i-1}(1-\alpha_j) C(p)=i=1∑Kciαij=1∏i−1(1−αj)
其中 K K K为与 p p p对应的射线相交的高斯数量,密度 α i \alpha_i αi由2D高斯值与不透明度 α k \alpha_k αk相乘得到。
多视图深度图重建可根据下式进行:
D ( p ) = ∑ i = 1 K d i α i ∏ j = 1 i − 1 ( 1 − α j ) D(p)=\sum_{i=1}^{K}d_i\alpha_i\prod_{j=1}^{i-1}(1-\alpha_j) D(p)=i=1∑Kdiαij=1∏i−1(1−αj)
其中 d i d_i di为第 i i i个高斯到相机的距离。
与NeRF相比,3DGS的计算代价对图像分辨率不敏感,可渲染更高分辨率的图像,从而促进表达学习。
3.2 基元预测
本文将体素特征转化为一组3D高斯。
- 每个体素中心作为一个锚点,并使用MLP预测多个高斯基元的属性,包括相对体素中心的偏移量、球面谐波系数、不透明度、尺寸和旋转。
- 使用3DGS解码器渲染生成多视图图像 C ∈ R N × H × W × C C\in\mathbb R^{N\times H\times W\times C} C∈RN×H×W×C,并由当前帧的多视图图像监督。
3.3 高斯过滤
为减少预训练时的计算开销,本文还基于预测的不透明度,过滤了低置信度的高斯。
- 使用tanh激活函数 预测不透明度,并过滤值小于0的高斯。
4. 自监督体素速度估计
本文使用场景中物体的时间一致性,自监督地估计每个体素的速度,从而丰富表达并促进对动态场景的理解。
4.1 速度指导的体素变形
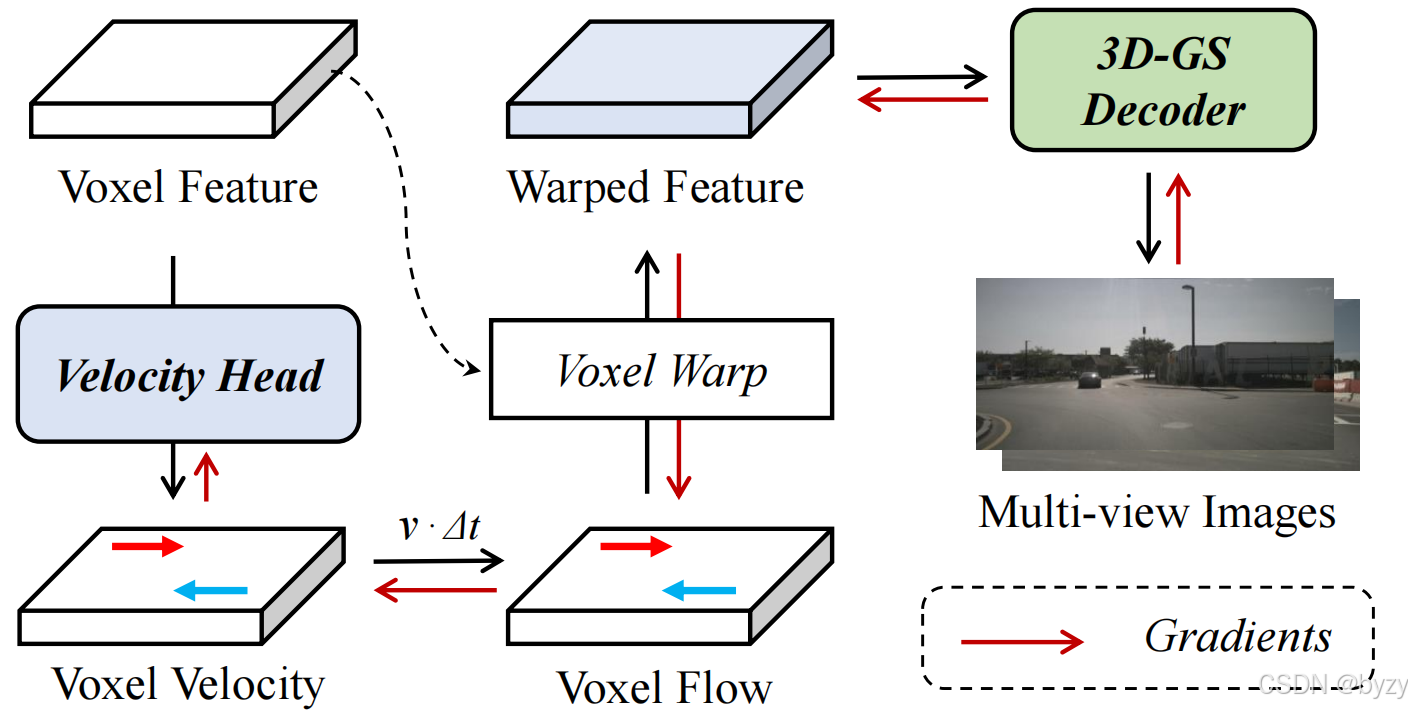
- 使用辅助速度头,预测体素在世界坐标系下的速度矢量。
- 通过将预测速度矢量乘以帧间隔估计体素流。
- 将当前帧体素移动到相邻帧中的估计位置(通过GridSample操作实施)。
4.2 相邻帧渲染
获取变形的相邻帧体素特征后,使用3DGS解码器渲染多视图图像,并与相应的相邻帧真实图像比较,计算损失。该损失只用于更新预测的体素速度,以使模型优先考虑学习运动特征。
5. 光度一致性
光度一致性用于进行自监督的深度估计,利用目标帧 I t I_t It的预测深度图,将源帧 I t ′ I_{t'} It′重投影到源视角下:
I t ′ → t = I t ′ < p r o j ( D t , T t → t ′ , K ) > I_{t'\rightarrow t}=I_{t'}\left<proj(D_t,T_{t\rightarrow t'},K)\right> It′→t=It′⟨proj(Dt,Tt→t′,K)⟩
其中 < ⋅ > \left<\cdot\right> ⟨⋅⟩为可微网格采样(Grid Sample)操作, D t D_t Dt为目标帧的预测深度图, T t → t ′ T_{t\rightarrow t'} Tt→t′为将点从 t t t时刻变换到 t ′ t' t′时刻的相对姿态, K K K为相机内参。 p r o j ( ⋅ ) proj(\cdot) proj(⋅)为根据预测深度 D t D_t Dt计算的源帧 I t ′ I_{t'} It′中的像素坐标。光度损失计算如下:
L p c = α ( 1 − S S I M ( I t , I t ′ → t ) ) + ( 1 − α ) ∥ I t − I t ′ → t ∥ 1 L_{pc}=\alpha(1-SSIM(I_t,I_{t'\rightarrow t}))+(1-\alpha)\|I_t-I_{t'\rightarrow t}\|_1 Lpc=α(1−SSIM(It,It′→t))+(1−α)∥It−It′→t∥1
其中 I t I_t It为目标帧, I t ′ → t I_{t'\rightarrow t} It′→t为重投影图像。 α \alpha α为损失平衡权重。
当前帧渲染的深度图像 D t D_t Dt可按下式得到:
D t = 3 D G S ( V t . K t , T t ) D_t=3DGS(V_t.K_t,T_t) Dt=3DGS(Vt.Kt,Tt)
其中 V t , K t , T t V_t,K_t,T_t Vt,Kt,Tt分别为体素特征,相机内参和外参。
6. 预训练损失
包括当前帧的L1重建损失、L1速度估计损失和光度一致性损失。