目录
[1. 拉格朗日插值(Lagrange Interpolation)](#1. 拉格朗日插值(Lagrange Interpolation))
[2. 均差(Divided Differences)](#2. 均差(Divided Differences))
[3. 牛顿插值多项式(Newton Interpolation)](#3. 牛顿插值多项式(Newton Interpolation))
[4. 埃尔米特插值(Hermite Interpolation)](#4. 埃尔米特插值(Hermite Interpolation))
[5. 分段线性插值(Piecewise Linear Interpolation)](#5. 分段线性插值(Piecewise Linear Interpolation))
[6. 三次样条插值(Cubic Spline Interpolation)](#6. 三次样条插值(Cubic Spline Interpolation))
一、实验任务
分别用拉格朗日插值、均差、牛顿插值多项式、埃尔米特插值、分段低次插值和三次样条插值测试函数和可视化对比,展示各方法的插值效果。
二、算法原理
1. 拉格朗日插值(Lagrange Interpolation)
数学原理
拉格朗日插值通过构造一组基函数,将插值多项式表示为已知点函数值的线性组合。对于给定的 n+1 个互异点 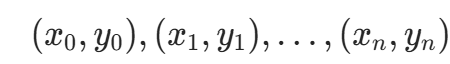 ,满足
,满足 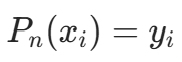 的 n 次插值多项式为:
的 n 次插值多项式为:
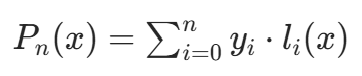
其中 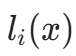 为拉格朗日基函数,定义为:
为拉格朗日基函数,定义为:
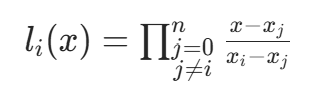
基函数的性质: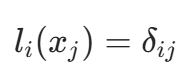 (克罗内克符号,即 i=j 时为 1,否则为 0)。
(克罗内克符号,即 i=j 时为 1,否则为 0)。
推导过程
- 假设插值多项式可表示为
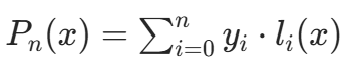 ,需满足
,需满足 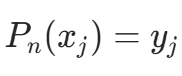 。
。 - 代入
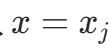 得
得 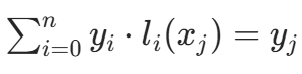 ,因此需
,因此需 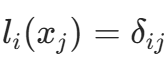 。
。 - 构造
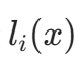 :当
:当 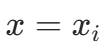 时取值为 1,当
时取值为 1,当 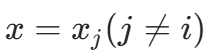 时取值为 0,故分子为
时取值为 0,故分子为 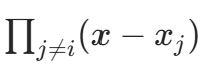 ,分母为
,分母为 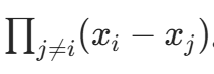 。
。
代码如下:
python
def lagrange_interpolation(x, y, xi):
n = len(x)
yi = 0
for i in range(n):
L = 1 # 基函数l_i(xi)
for j in range(n):
if j != i:
L *= (xi - x[j]) / (x[i] - x[j]) # 计算基函数乘积
yi += y[i] * L # 累加y_i * l_i(xi)
return yi2. 均差(Divided Differences)
数学原理
均差是牛顿插值的基础,用于衡量函数在不同点的平均变化率。定义:
- 零阶均差:
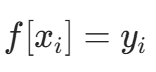
- 一阶均差:
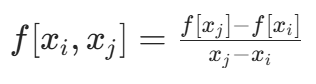
- k 阶均差:
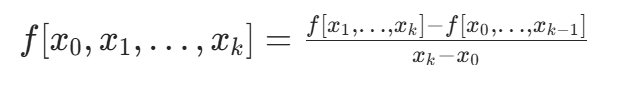
均差具有对称性:与点的顺序无关,即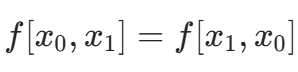 。
。
推导过程
均差是递归定义的,高阶均差由低阶均差计算。例如,二阶均差: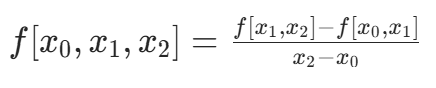
其物理意义是 "一阶均差的均差",反映函数的二阶变化率。
代码如下:
python
def divided_diff(x, y):
n = len(x)
dd = np.zeros((n, n)) # dd[i][j]表示f[x_i-j, ..., x_i]
dd[:, 0] = y # 零阶均差
for j in range(1, n): # j为阶数
for i in range(j, n): # i为终点索引
dd[i, j] = (dd[i, j-1] - dd[i-1, j-1]) / (x[i] - x[i-j])
return dd3. 牛顿插值多项式(Newton Interpolation)
数学原理
牛顿插值多项式利用均差构造,形式为: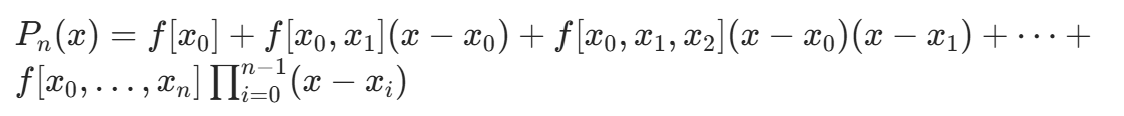
与拉格朗日插值相比,牛顿插值的优势是新增数据点时可增量计算,无需重新构造整个多项式。
推导过程
- 定义
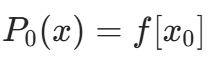 (零次多项式)。
(零次多项式)。 - 一次多项式:
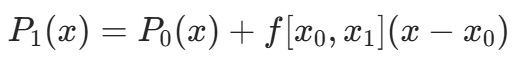 ,满足
,满足 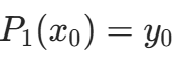 且
且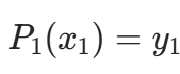 。
。 - 递归扩展:
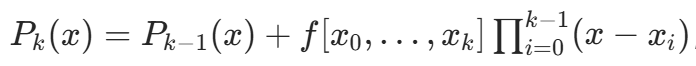 ,确保
,确保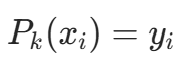 对
对 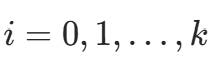 成立。
成立。
代码如下:
python
def newton_interpolation(x, y, xi):
n = len(x)
dd = divided_diff(x, y) # 获取均差表
result = dd[0, 0] # 初始项:f[x0]
for i in range(1, n):
term = dd[i, i] # 第i阶均差系数
for j in range(i):
term *= (xi - x[j]) # 乘(x-x0)(x-x1)...(x-x(i-1))
result += term # 累加项
return result4. 埃尔米特插值(Hermite Interpolation)
数学原理
埃尔米特插值不仅要求插值多项式与原函数在节点处函数值相等,还要求导数值相等。对于 n+1 个点 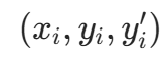 (已知函数值和导数值),构造 2n+1 次多项式 H(x) 满足:
(已知函数值和导数值),构造 2n+1 次多项式 H(x) 满足: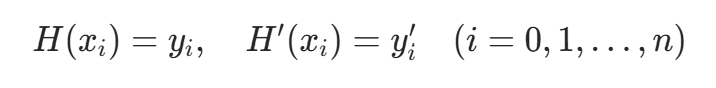
推导过程
- 引入扩展节点
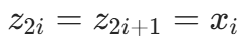 (每个节点重复两次),函数值
(每个节点重复两次),函数值 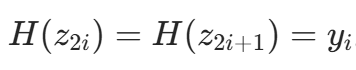 。
。 - 利用均差公式处理导数条件:当节点重合时,一阶均差定义为导数
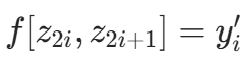 ,高阶均差通过递归计算。
,高阶均差通过递归计算。 - 牛顿形式的埃尔米特多项式:
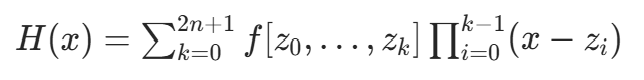
代码如下:
python
def hermite_interpolation(x, y, y_prime, xi):
n = len(x)
m = 2 * n # 扩展节点数:每个点含函数值和导数值
z = np.zeros(m) # 扩展节点z = [x0, x0, x1, x1, ..., xn, xn]
H = np.zeros(m) # 扩展函数值H = [y0, y0, y1, y1, ..., yn, yn]
for i in range(n):
z[2*i] = z[2*i + 1] = x[i]
H[2*i] = H[2*i + 1] = y[i]
# 计算均差表,处理导数条件
dd = np.zeros((m, m))
dd[:, 0] = H
for j in range(1, m):
for i in range(j, m):
if z[i] == z[i-j]: # 节点重合(处理导数)
if j == 1:
dd[i, j] = y_prime[i//2] # 一阶均差=导数
else:
dd[i, j] = dd[i, j-1] / (z[i] - z[i-j+1])
else:
dd[i, j] = (dd[i, j-1] - dd[i-1, j-1]) / (z[i] - z[i-j])
# 计算插值结果(牛顿形式)
result = dd[0, 0]
for i in range(1, m):
term = dd[i, i]
for j in range(i):
term *= (xi - z[j])
result += term
return result5. 分段线性插值(Piecewise Linear Interpolation)
数学原理
分段线性插值将插值区间 [a,b] 按节点 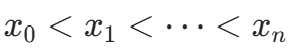 分为子区间
分为子区间 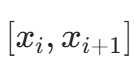 ,在每个子区间内用线性函数逼近原函数:
,在每个子区间内用线性函数逼近原函数: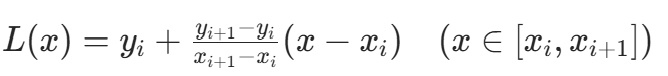
特点:避免高次插值的震荡现象,函数连续但导数不连续。
推导过程
- 在子区间
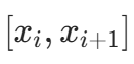 内构造线性函数
内构造线性函数 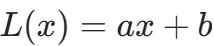 。
。 - 代入边界条件
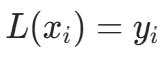 和
和 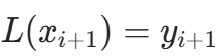 ,解得:
,解得: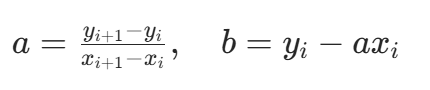
- 整理得线性插值公式。
代码如下:
python
def piecewise_linear_interpolation(x, y, xi):
n = len(x)
for i in range(n-1):
if x[i] <= xi <= x[i+1]: # 找到xi所在区间
# 线性插值公式
return y[i] + (y[i+1] - y[i]) * (xi - x[i]) / (x[i+1] - x[i])
# 边界外处理:最近邻插值
return y[0] if xi < x[0] else y[-1]6. 三次样条插值(Cubic Spline Interpolation)
数学原理
三次样条插值是分段三次多项式,满足:
- 在每个子区间
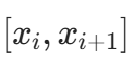 内为三次多项式
内为三次多项式 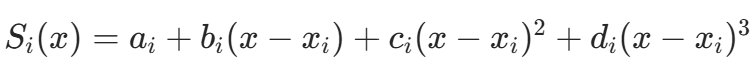 。
。 - 函数值连续:
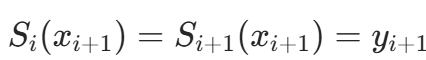 。
。 - 一阶导数连续:
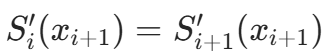 。
。 - 二阶导数连续:
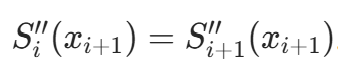 。
。
边界条件: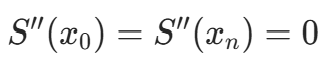 。
。
推导过程
- 设
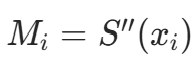 (二阶导数在节点的值),则三次多项式可表示为:
(二阶导数在节点的值),则三次多项式可表示为: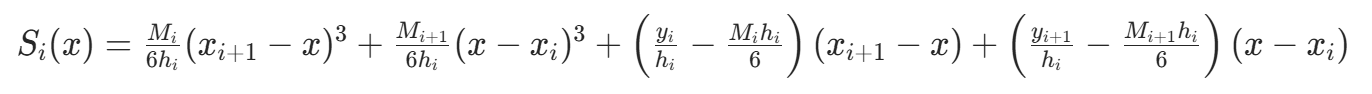 其中
其中 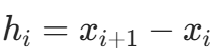 。
。 - 利用一阶导数连续条件推导得关于 Mi 的三对角方程组:
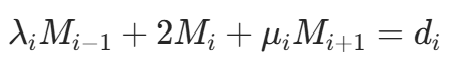 ,其中
,其中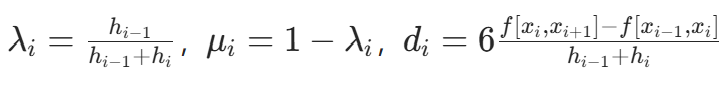 。
。 - 求解方程组得
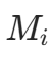 ,代入多项式表达式即得插值函数。
,代入多项式表达式即得插值函数。
代码如下:
代码中使用 scipy.interpolate.CubicSpline 实现,采用自然边界条件(bctype=′natural′):
python
cs = CubicSpline(x, y, bc_type='natural') # 构造三次样条
y_spline = cs(x_interp) # 计算插值结果总结
六种插值方法各有特点:
- 拉格朗日 / 牛顿插值:全局多项式,高次时可能震荡。
- 埃尔米特插值:利用导数信息,精度更高。
- 分段线性插值:简单稳定,但光滑性差。
- 三次样条插值:兼顾精度与光滑性,应用最广泛。
三、Python代码完整展示
python
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
import matplotlib.gridspec as gridspec
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False # 解决负号显示问题
# 1. 拉格朗日插值
def lagrange_interpolation(x, y, xi):
"""
拉格朗日插值
x: 已知点的x坐标
y: 已知点的y坐标
xi: 插值点的x坐标
"""
n = len(x)
yi = 0
for i in range(n):
# 计算拉格朗日基函数
L = 1
for j in range(n):
if j != i:
L *= (xi - x[j]) / (x[i] - x[j])
yi += y[i] * L
return yi
# 2. 均差计算
def divided_diff(x, y):
"""计算均差表"""
n = len(x)
dd = np.zeros((n, n)) # 均差表
dd[:, 0] = y # 零阶均差
for j in range(1, n):
for i in range(j, n):
dd[i, j] = (dd[i, j - 1] - dd[i - 1, j - 1]) / (x[i] - x[i - j])
return dd
# 3. 牛顿插值多项式
def newton_interpolation(x, y, xi):
"""牛顿插值"""
n = len(x)
dd = divided_diff(x, y) # 获取均差表
result = dd[0, 0]
for i in range(1, n):
term = dd[i, i]
for j in range(i):
term *= (xi - x[j])
result += term
return result
# 4. 埃尔米特插值
def hermite_interpolation(x, y, y_prime, xi):
"""
埃尔米特插值(同时插值函数值和导数值)
x: 已知点的x坐标
y: 已知点的y坐标
y_prime: 已知点的导数值
xi: 插值点的x坐标
"""
n = len(x)
m = 2 * n # 总点数(每个点包含函数值和导数值)
H = np.zeros(m) # 埃尔米特插值多项式的系数
z = np.zeros(m) # 扩展的x坐标
# 初始化扩展的x坐标和函数值
for i in range(n):
z[2 * i] = x[i]
z[2 * i + 1] = x[i]
H[2 * i] = y[i]
H[2 * i + 1] = y[i]
# 计算均差表
dd = np.zeros((m, m))
dd[:, 0] = H
for j in range(1, m):
for i in range(j, m):
if z[i] == z[i - j]:
# 处理导数情况
if j == 1:
dd[i, j] = y_prime[i // 2]
else:
dd[i, j] = dd[i, j - 1] / (z[i] - z[i - j + 1])
else:
dd[i, j] = (dd[i, j - 1] - dd[i - 1, j - 1]) / (z[i] - z[i - j])
# 计算插值结果
result = dd[0, 0]
for i in range(1, m):
term = dd[i, i]
for j in range(i):
term *= (xi - z[j])
result += term
return result
# 5. 分段线性插值
def piecewise_linear_interpolation(x, y, xi):
"""分段线性插值"""
n = len(x)
# 找到xi所在的区间
for i in range(n - 1):
if x[i] <= xi <= x[i + 1]:
# 线性插值
return y[i] + (y[i + 1] - y[i]) * (xi - x[i]) / (x[i + 1] - x[i])
# 如果超出范围,使用最近邻插值
return y[0] if xi < x[0] else y[-1]
# 生成测试数据
def generate_test_data(func, start, end, n_points, noise=0):
"""生成测试数据点"""
x = np.linspace(start, end, n_points)
y = func(x) + noise * np.random.randn(n_points)
# 计算导数值(用于埃尔米特插值)
h = 1e-6
y_prime = (func(x + h) - func(x - h)) / (2 * h)
return x, y, y_prime
# 可视化所有插值方法
def visualize_interpolations():
# 定义原函数
def original_function(x):
return np.sin(x) + 0.5 * x # 示例函数:sin(x) + 0.5x
# 生成稀疏数据点
x, y, y_prime = generate_test_data(original_function, 0, 2 * np.pi, 6)
# 生成密集的插值点
x_interp = np.linspace(0, 2 * np.pi, 200)
y_true = original_function(x_interp)
# 计算各种插值结果
y_lagrange = [lagrange_interpolation(x, y, xi) for xi in x_interp]
y_newton = [newton_interpolation(x, y, xi) for xi in x_interp]
y_hermite = [hermite_interpolation(x, y, y_prime, xi) for xi in x_interp]
y_piecewise = [piecewise_linear_interpolation(x, y, xi) for xi in x_interp]
# 三次样条插值(使用scipy)
cs = CubicSpline(x, y, bc_type='natural') # 自然边界条件
y_spline = cs(x_interp)
# 计算均差表(用于展示)
dd_table = divided_diff(x, y)
n = len(x)
max_order = n - 1 # 最大阶数
# 创建图形
plt.figure(figsize=(15, 12))
gs = gridspec.GridSpec(3, 2, hspace=0.3, wspace=0.2)
# 1. 拉格朗日插值
ax1 = plt.subplot(gs[0, 0])
ax1.plot(x_interp, y_true, 'b-', label='原函数')
ax1.plot(x_interp, y_lagrange, 'r--', label='拉格朗日插值')
ax1.scatter(x, y, color='black', label='数据点')
ax1.set_title('拉格朗日插值')
ax1.legend()
ax1.grid(True, alpha=0.3)
# 2. 牛顿插值
ax2 = plt.subplot(gs[0, 1])
ax2.plot(x_interp, y_true, 'b-', label='原函数')
ax2.plot(x_interp, y_newton, 'g--', label='牛顿插值')
ax2.scatter(x, y, color='black', label='数据点')
ax2.set_title('牛顿插值')
ax2.legend()
ax2.grid(True, alpha=0.3)
# 3. 埃尔米特插值
ax3 = plt.subplot(gs[1, 0])
ax3.plot(x_interp, y_true, 'b-', label='原函数')
ax3.plot(x_interp, y_hermite, 'm--', label='埃尔米特插值')
ax3.scatter(x, y, color='black', label='数据点')
ax3.set_title('埃尔米特插值')
ax3.legend()
ax3.grid(True, alpha=0.3)
# 4. 分段线性插值
ax4 = plt.subplot(gs[1, 1])
ax4.plot(x_interp, y_true, 'b-', label='原函数')
ax4.plot(x_interp, y_piecewise, 'c--', label='分段线性插值')
ax4.scatter(x, y, color='black', label='数据点')
ax4.set_title('分段线性插值')
ax4.legend()
ax4.grid(True, alpha=0.3)
# 5. 三次样条插值
ax5 = plt.subplot(gs[2, 0])
ax5.plot(x_interp, y_true, 'b-', label='原函数')
ax5.plot(x_interp, y_spline, 'y--', label='三次样条插值')
ax5.scatter(x, y, color='black', label='数据点')
ax5.set_title('三次样条插值')
ax5.legend()
ax5.grid(True, alpha=0.3)
# 6. 均差表示(修复了列数不一致的问题)
ax6 = plt.subplot(gs[2, 1])
ax6.axis('off')
# 表头
header = ['x_i', 'f(x_i)'] + [f'{i}阶均差' for i in range(1, max_order + 1)]
table_data = [header]
# 数据行
for i in range(n):
row = [f'{x[i]:.4f}', f'{y[i]:.4f}']
# 添加各阶均差,确保每行有相同数量的列
for j in range(1, max_order + 1):
if j <= i: # 只有当阶数小于等于当前行索引时才有值
row.append(f'{dd_table[i, j]:.4f}')
else: # 否则填充空字符串
row.append('')
table_data.append(row)
table = ax6.table(cellText=table_data, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(8)
table.scale(1.2, 1.2)
ax6.set_title('均差表')
plt.tight_layout()
plt.savefig('插值法.png')
plt.show()
if __name__ == "__main__":
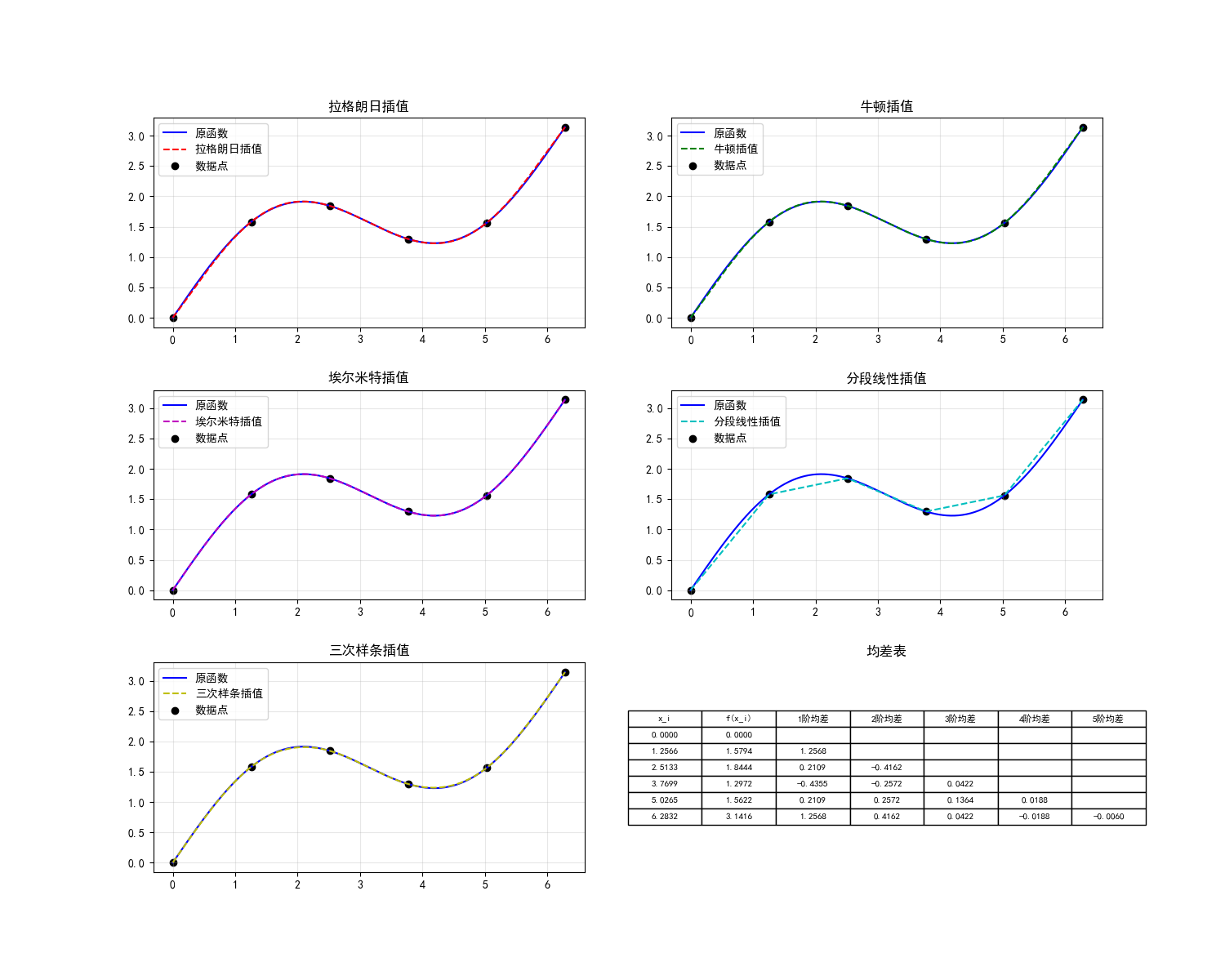
visualize_interpolations()四、程序运行结果展示
五、总结
本文对比了六种插值方法在测试函数f(x)=sin(x)+0.5x上的应用效果。通过Python实现拉格朗日插值、牛顿插值、埃尔米特插值、分段线性插值和三次样条插值,并可视化展示了各方法的拟合结果。实验结果表明:全局多项式方法(拉格朗日/牛顿)在高次时易出现震荡;埃尔米特插值利用导数信息精度更高;分段线性插值简单稳定但光滑性差;三次样条插值在精度和光滑性方面表现最优。文中详细阐述了每种方法的数学原理和实现代码,为不同应用场景下的插值方法选择提供了参考依据。