一、串的概念
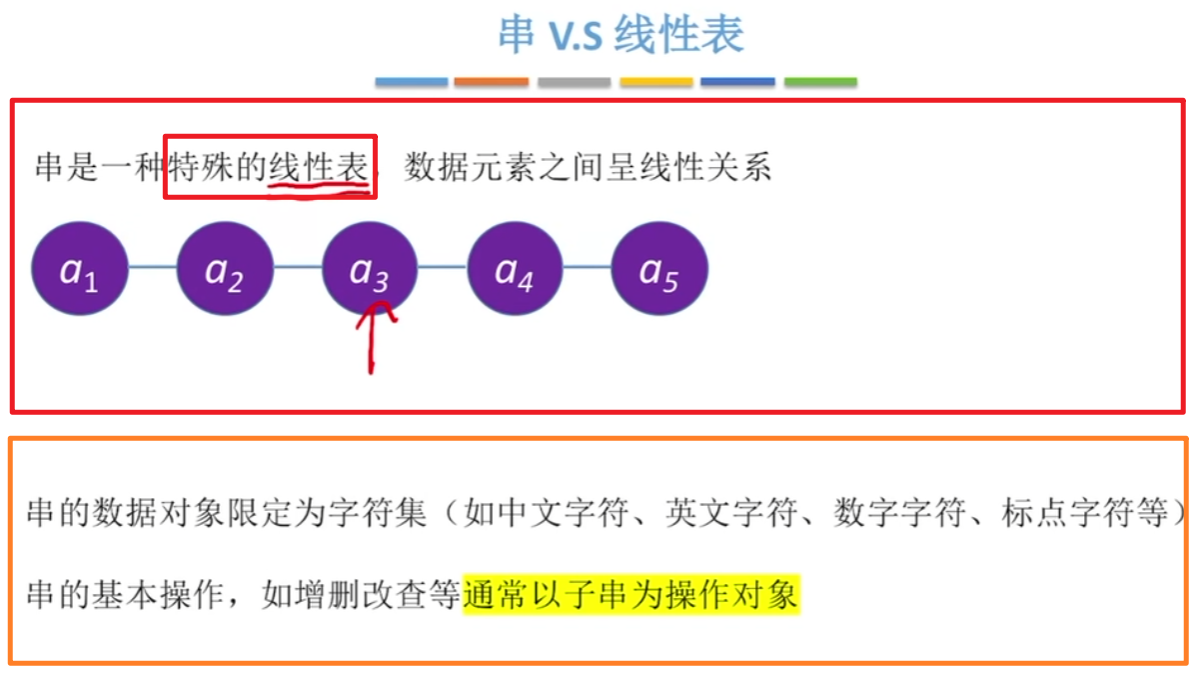
1、串的定义
太简单了就是代码里的字符串,跨专业的自己看下面图吧
2、串的操作
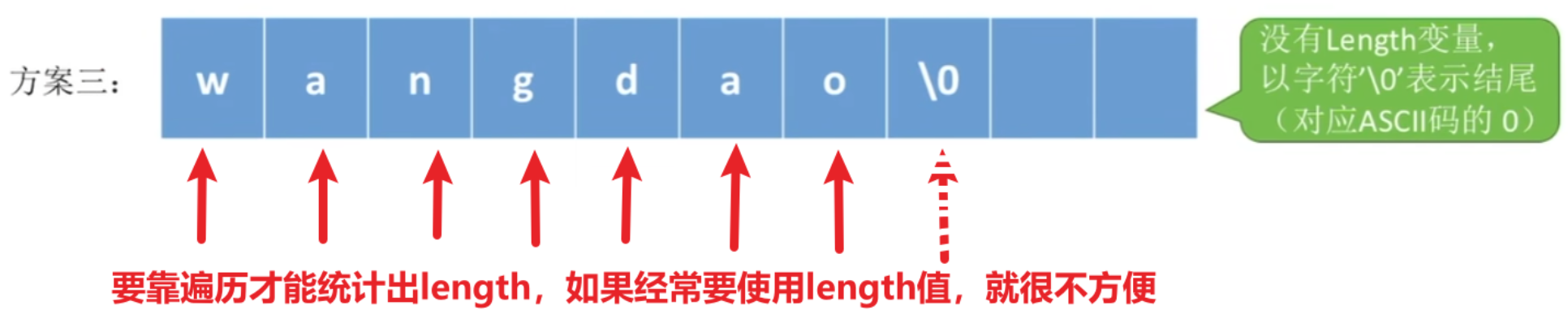
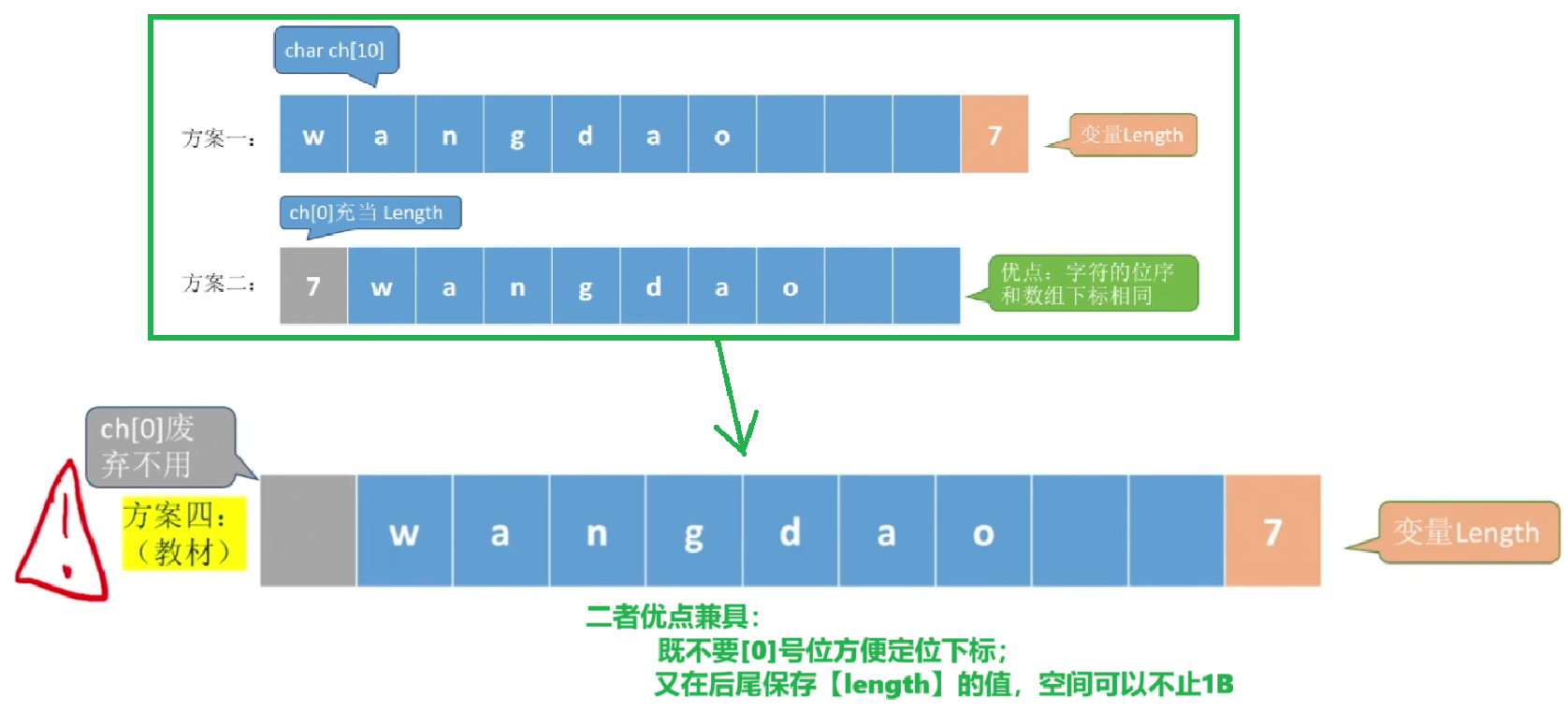
3、串的顺序结构
有这么四种方案,没什么好说的,哪怕是跨考的学一节应该也看得懂
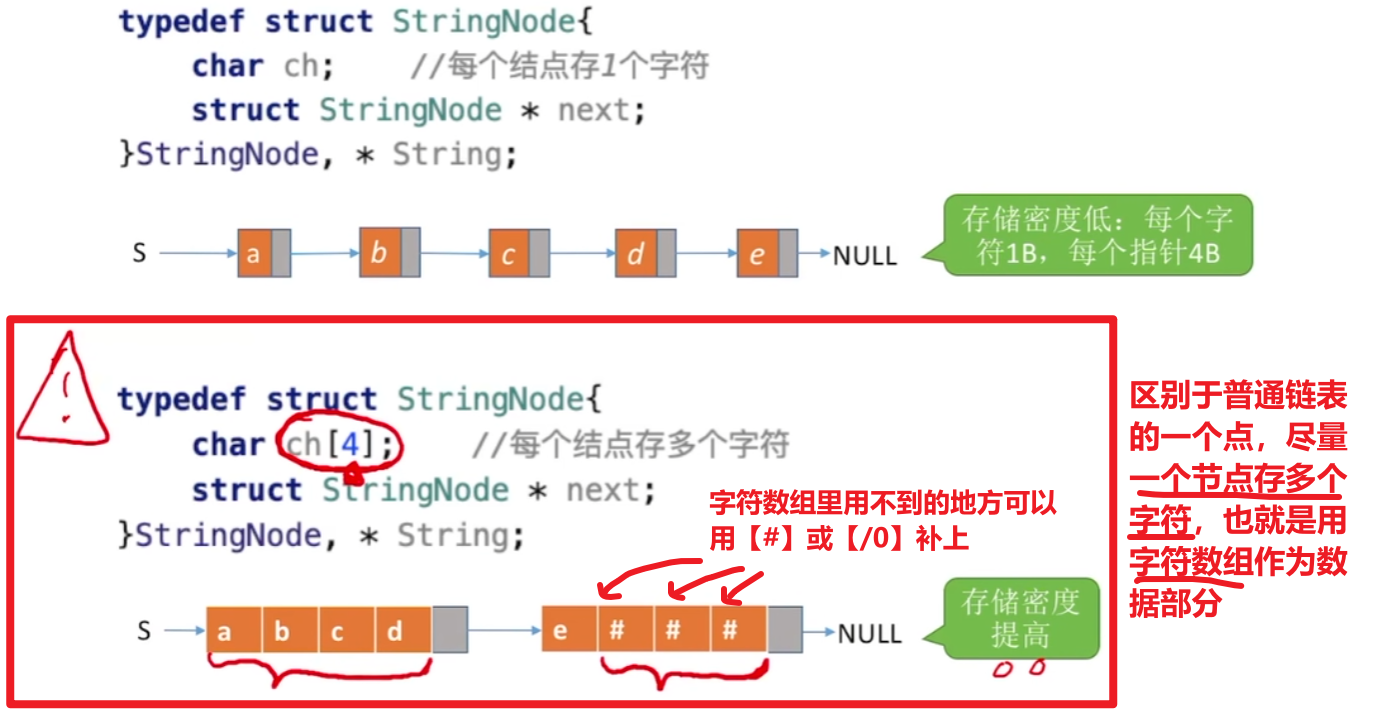
4、串的链式存储结构
依旧没什么好说的,看一眼就行
二、开始有用的部分
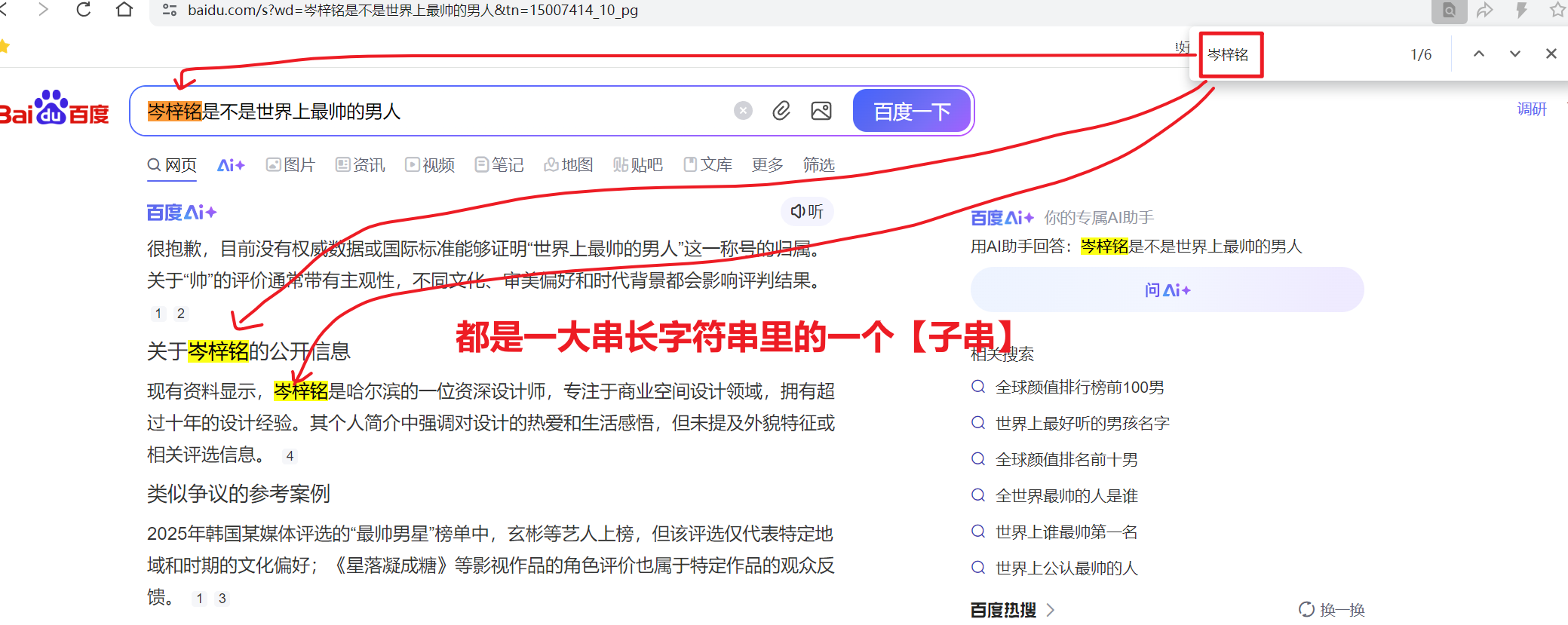
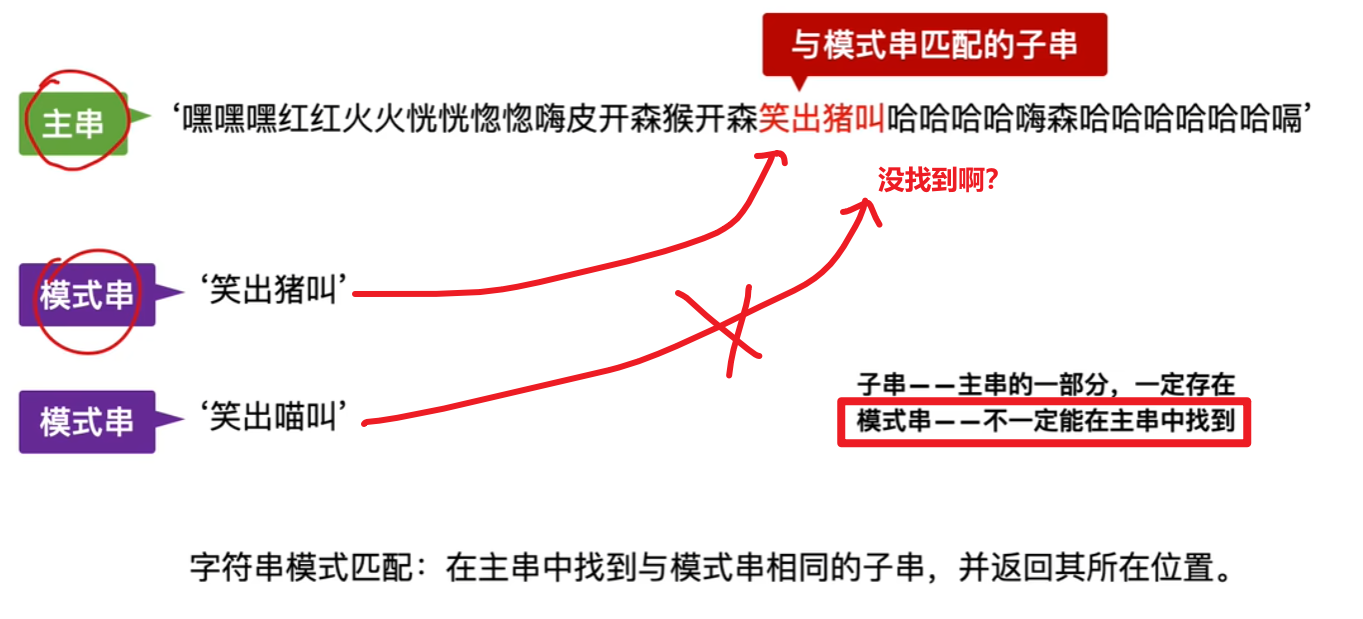
专业术语**【模式串**】解释:
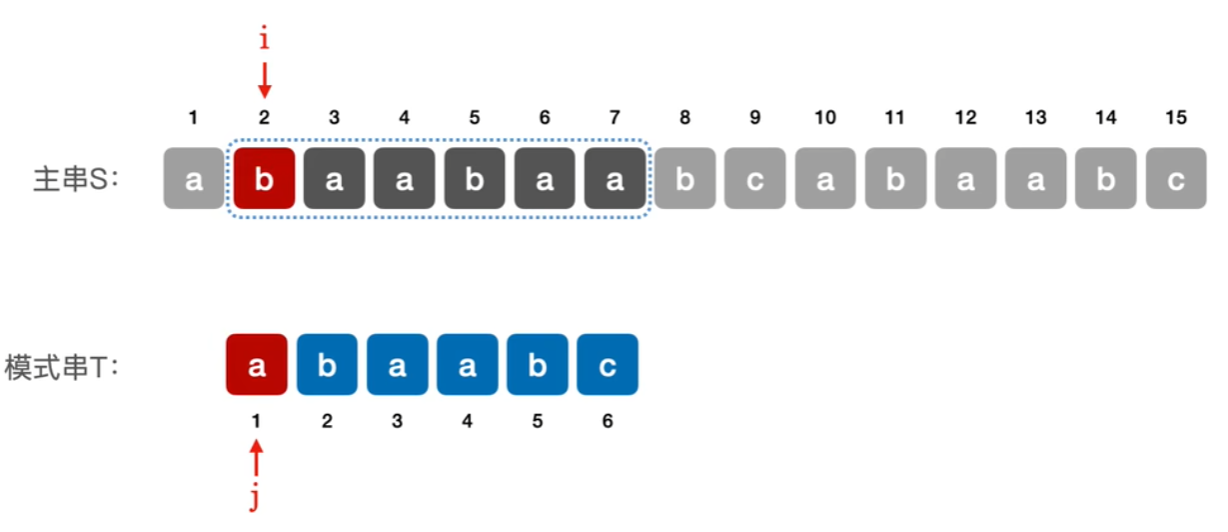
而这种在【主串】中找到某个和【模式串】匹配的【子串】,并返回该【子串第1个字符在主串的位置】的运算就叫------------------【模式匹配】
1、朴素模式匹配算法
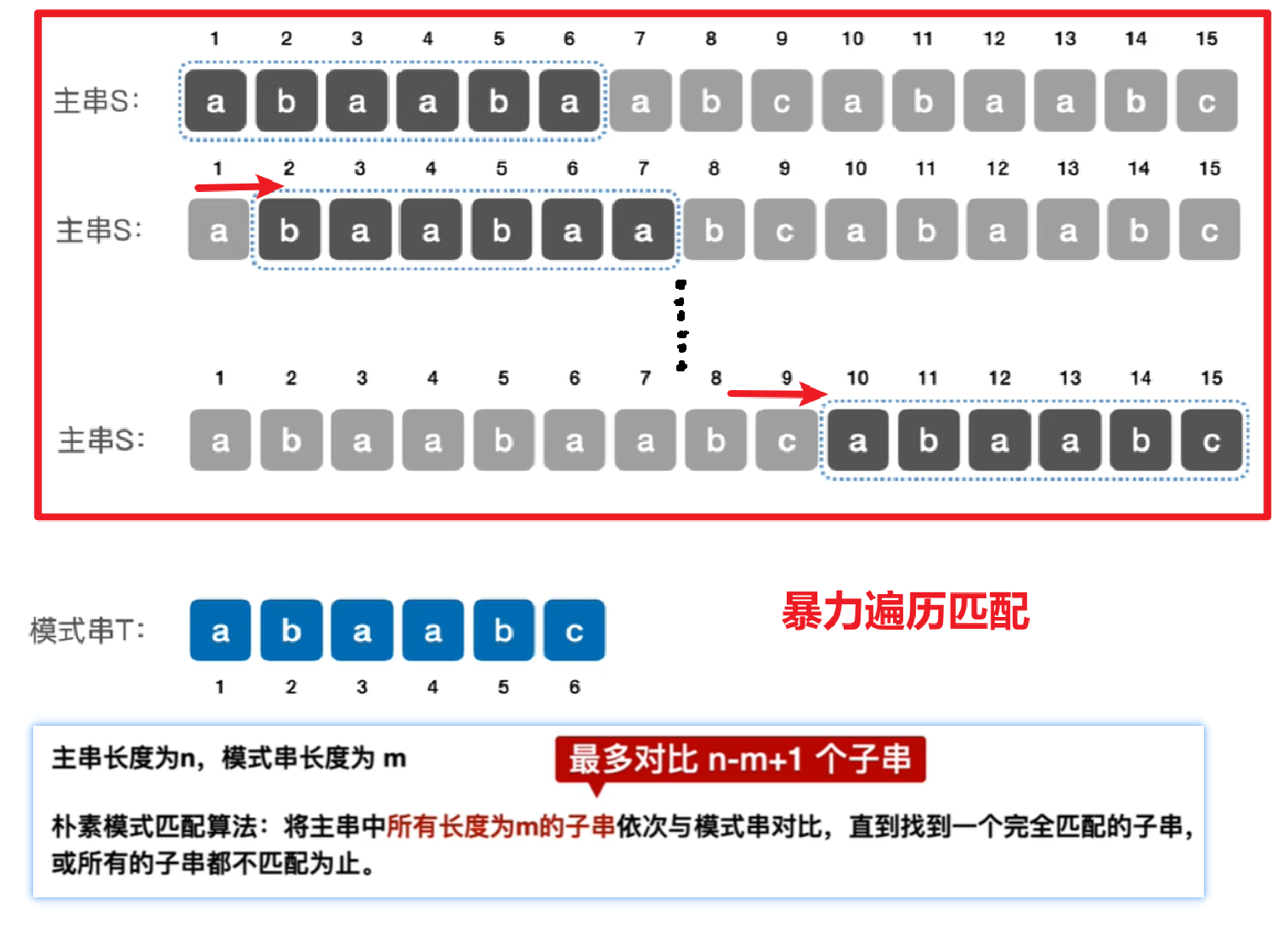
没什么好说的,写过代码的应该看得懂下面图,就是【主串】取【和模式串一样长的子串】一一对比,一旦不同,【主串的子串】整体往后挪一位,又从头开始一一对比
可以记一下,主串长度n、模式串长度m,看上面图主串里的【子串的头】最多移动到【n-m+1位】,也就是最多对比【n-m+1】个子串
;
;
然后简单记一下代码逻辑:
- 1、遍历【主串的指针i】和【遍历模式串的指针j】初始位置都是0
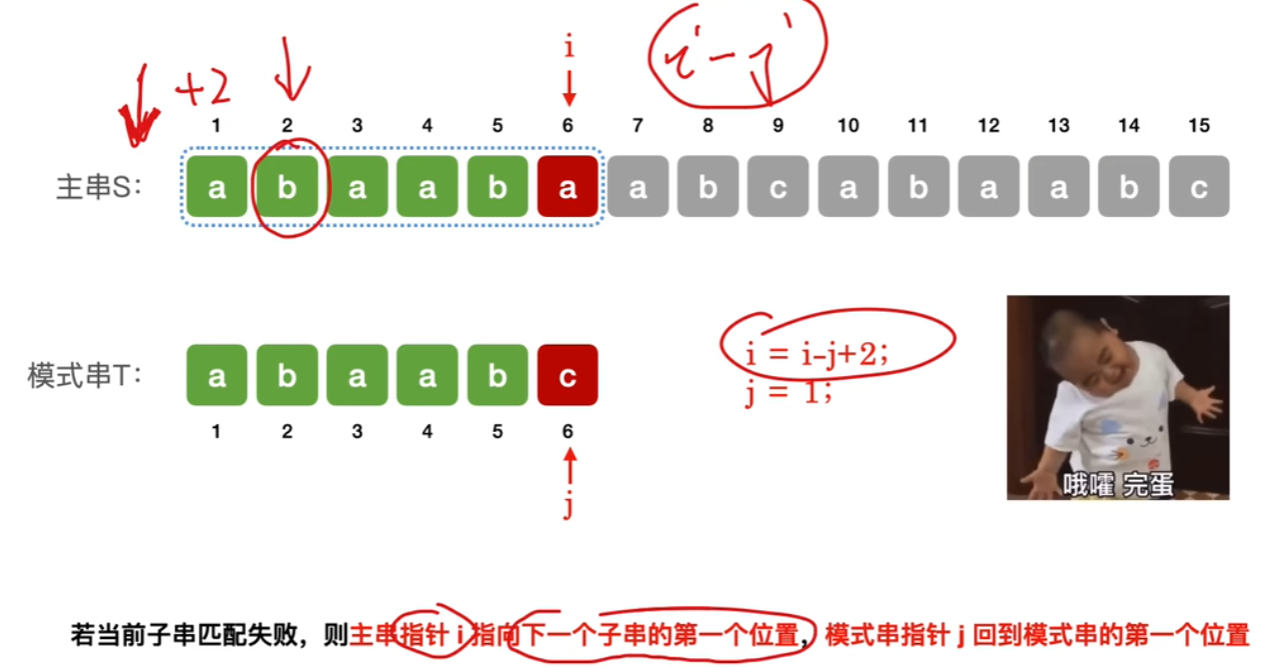
- 2、若某一位匹配失败,因为i和j都是对应子串相对一样 的位置,那么:
- 【i】就应该等于【i-j+2】,因为:
- 【i-j】就是回到**主串的【当前子串】**的开头前一位
- 【i-j+1】就是回到**主串的【当前子串】**的开头第一位
- 【i-j+2】就是回到主串的【当前子串】 的开头前二位,那么就可以以他为【下一个子串的开头第一个元素】
- 而【j】直接等于1,回到自己模式串的开头第一位即可
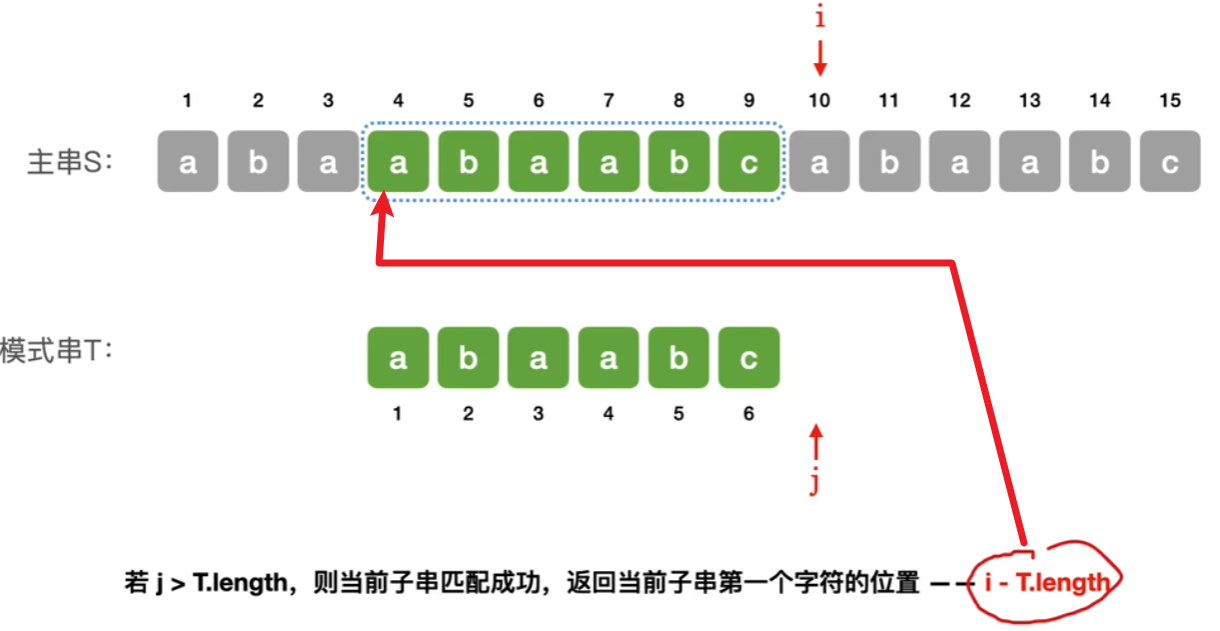
- 3、而如果找到了主串中【匹配模式串的子串】
- 那就很简单,返回【这个子串第一个字符的位置】
;
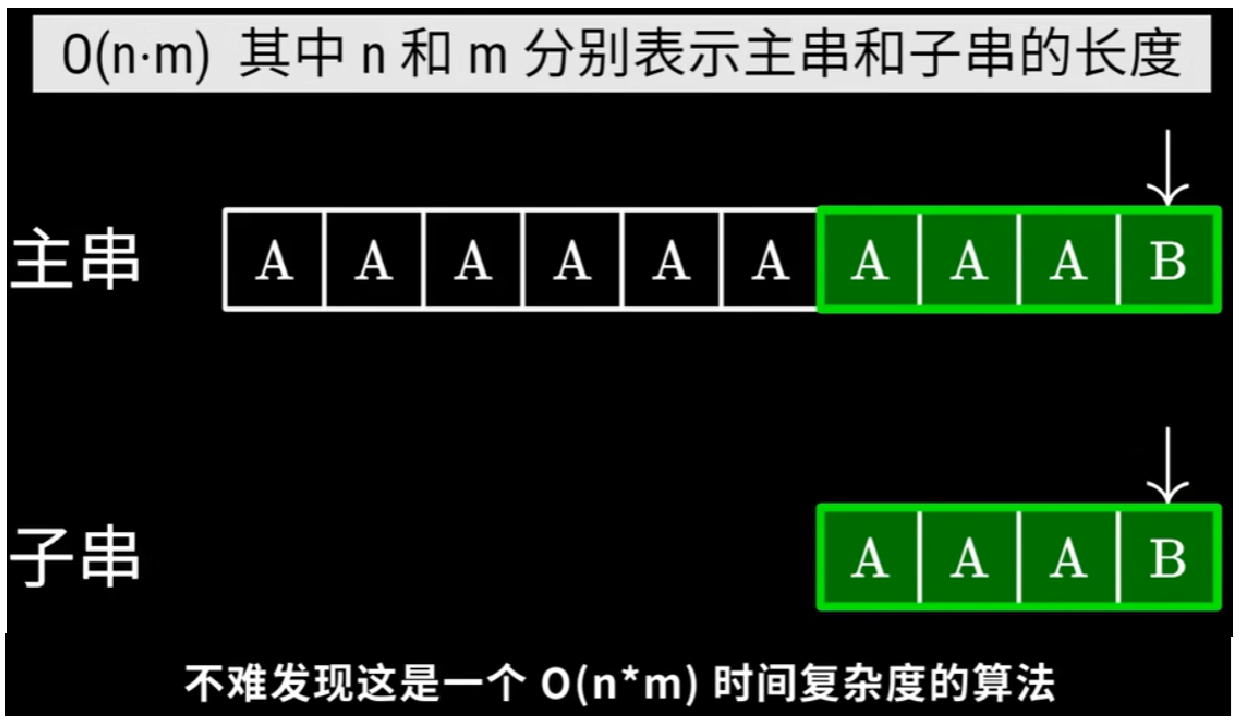
朴素模式匹配算法【时间复杂度】
- 主串长度n、模式串长度m,【时间复杂度:O(n*m)】
- 主串需要最多对比【n-m+1】个子串,就是近似n*m
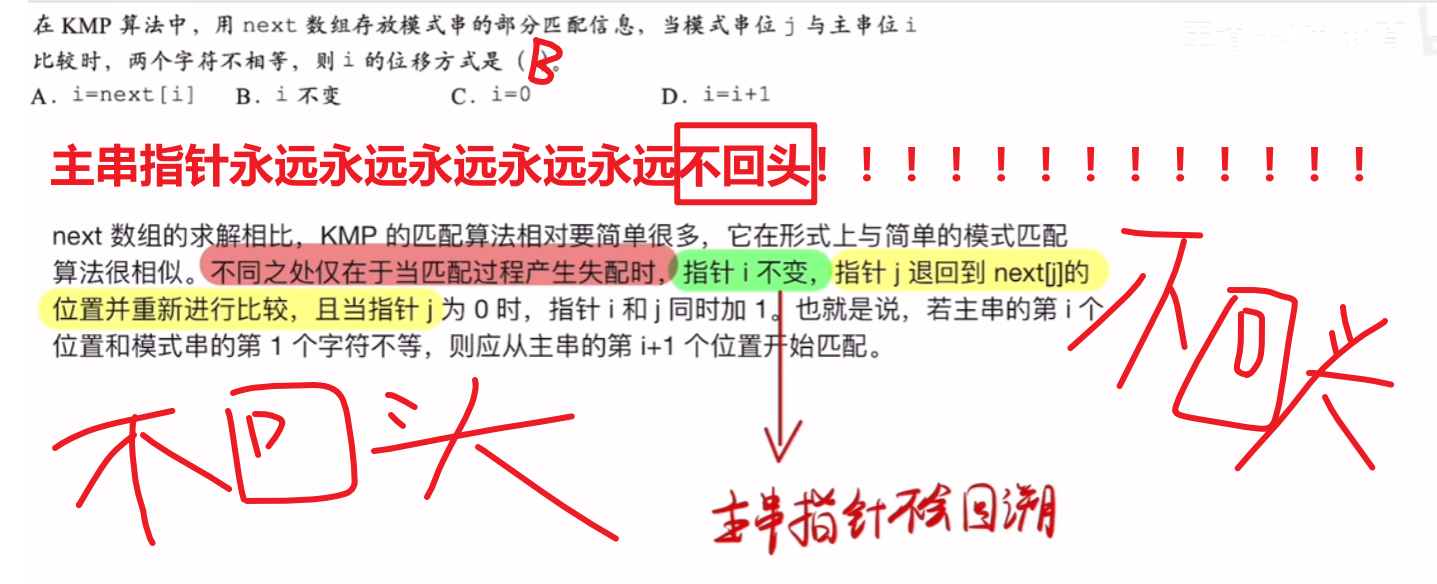
【例题】
2、KMP算法
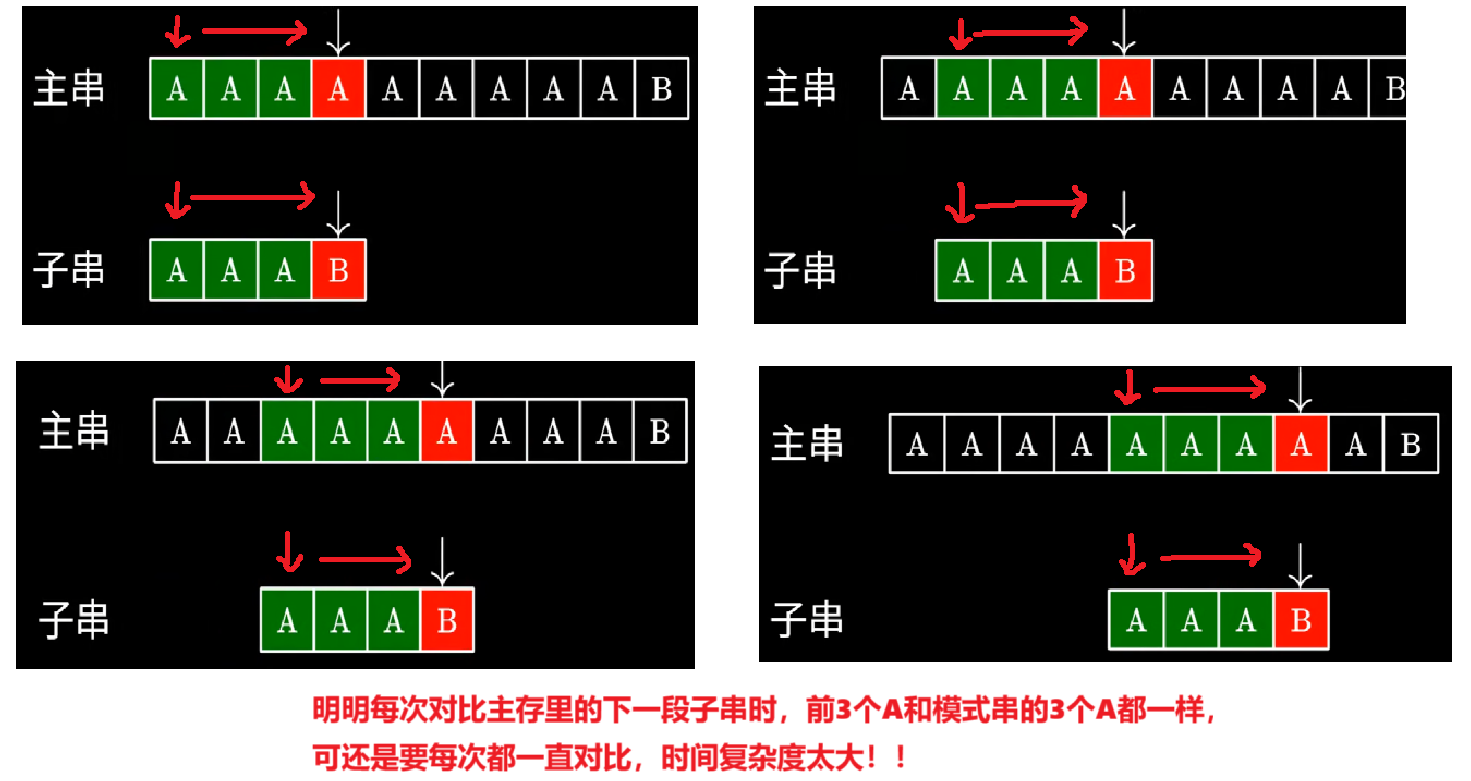
这玩意太几儿抽象了,必须先从人类视角解决概念,然后再讲具体实际程序运行是怎样的
1)纯抽象概念解释
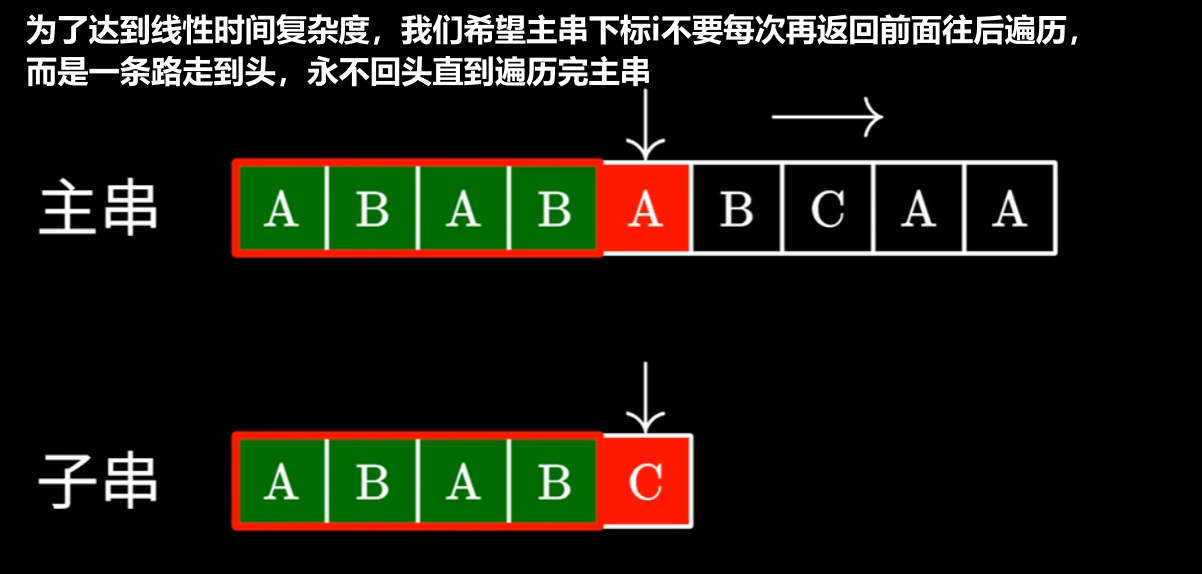
为了弥补朴素模式匹配算法太慢,KMP算法实现了线性的时间复杂度
【首先先不考虑计算机,仅从人的视角出发】:
- 一个【模式串】跟【主串的子串】对比时,既然双方指针都能遍历到后面,指针前的元素肯定是对应一样匹配的
- 就说明当出现不匹配时,我们没必要再把让它两再次回到头,从头往后对比
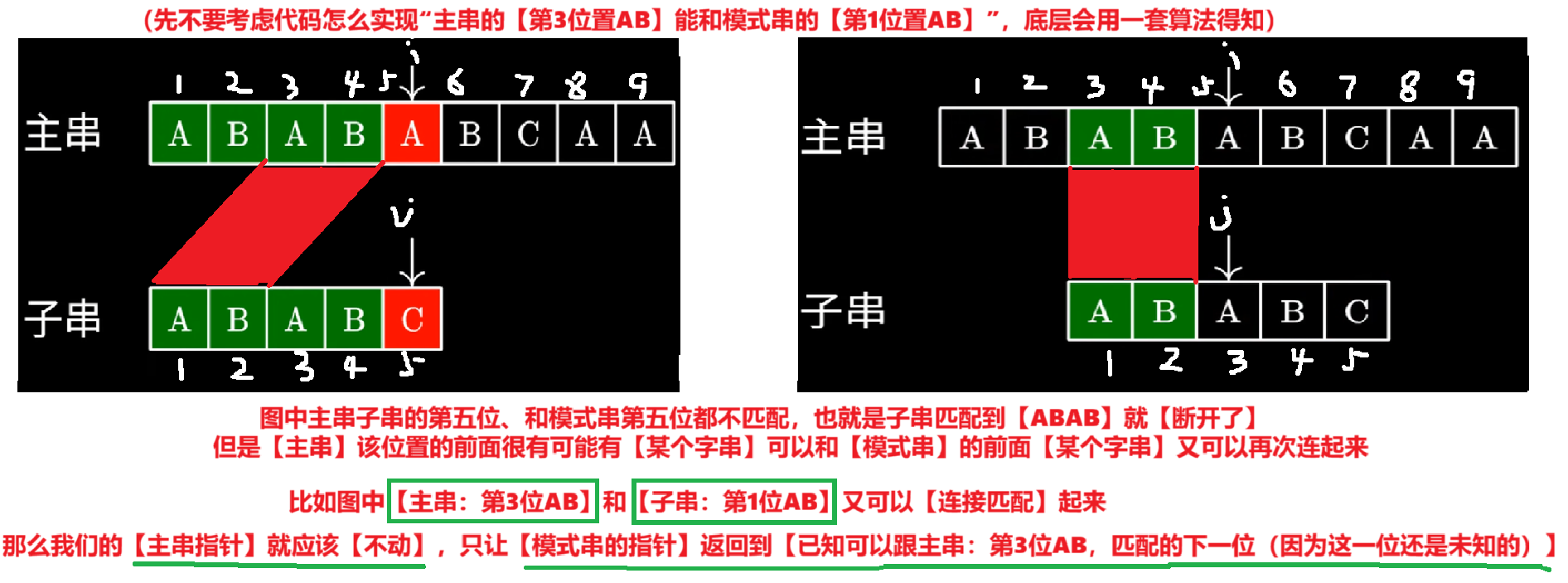
- 而是应该从【不匹配的那位字符】往前找到一个【前后缀】,在【模式串】里的【也有一样的前后缀】,既然都一样了,那就二者都跳过这个【相同前后缀】,从它的后一位开始对比
- 【主串的子串】的指针已经是在【相同前后缀】的后一位了,指针可以不用动
- 【模式串】的指针则需要跳到这个【相同前后缀】的后一位
- 那么如何实现让模式串找到这个**【相同前后缀】的后一位**?
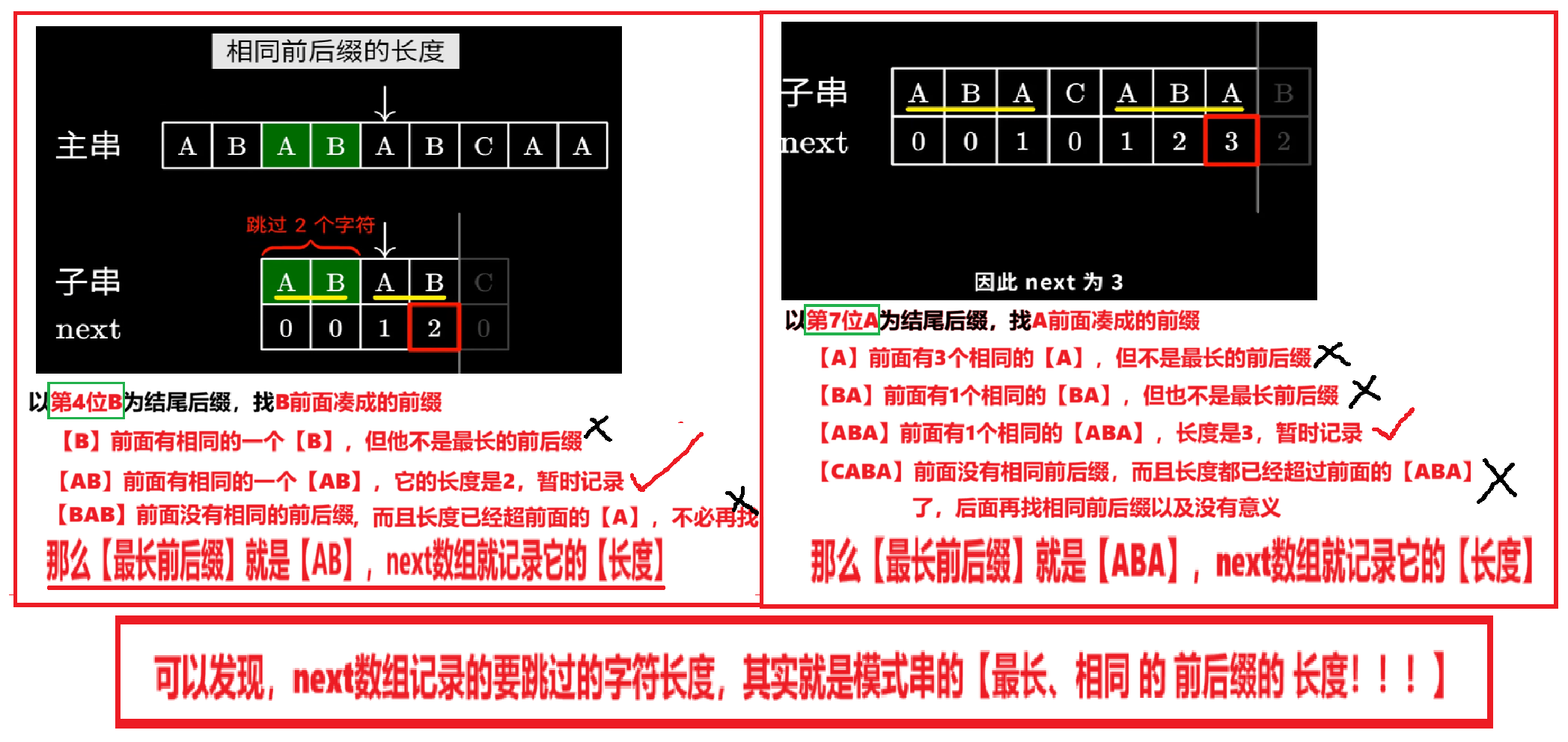
① 多加一个【next数组】用来统计模式串【每一位出现不匹配】时,对应的【指针应该跳到哪?】
② 而【next数组】的本质就是:记录模式串里,每一位【作为后缀、最长、有相同的前后缀的长度】
大概流程就是下图这样:
;
;
KMP模式匹配算法【时间复杂度】:
- 主串长度n、模式串长度m,【时间复杂度:O(n+m)】
- 主串只用一次性遍历一次,记住了是线性时间复杂度!!
2)具体程序怎么实现这逻辑?
现在,计算机视角,别特么管前面的什么逻辑了,计算机跟人不一样,我们直接暴力计算:
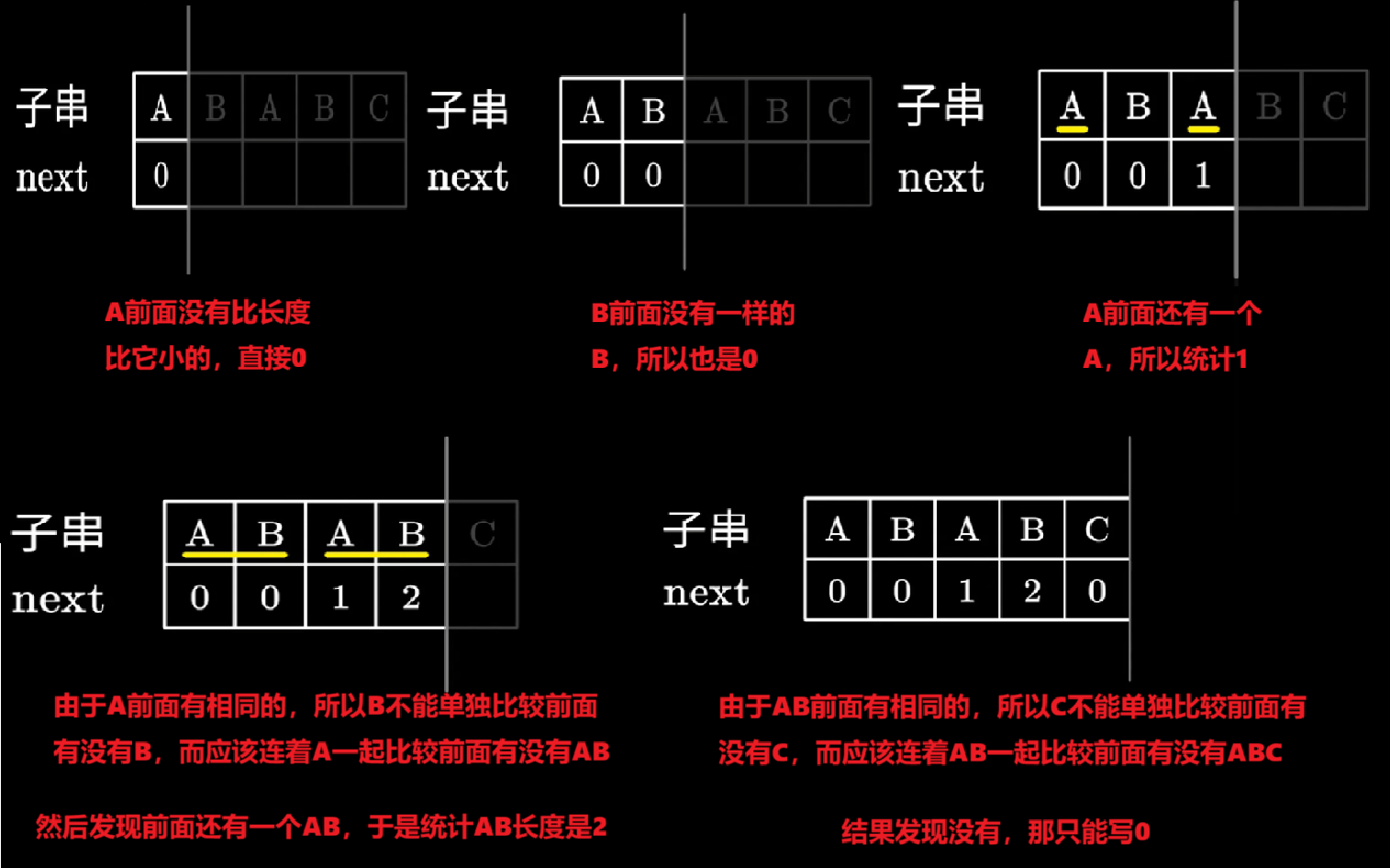
- 1、首先,在得出【next数组】时,我们还需要设置一个【PM数组】,别问为什么,我也不知道,我只知道老子考试做题就按这个步骤来
- 2、【PM数组】对应统计【模式串的每一位】前面的【最长相同前后缀】的【长度】
- 听不懂没关系,完全没关系,看流程照做就行
- 【第一步】:模式串第一位一定是0,什么都别管直接写0就行了
- 【第二步】:第1位和第2位对比,一样的话,第2位的值是0;不一样则第2位是0
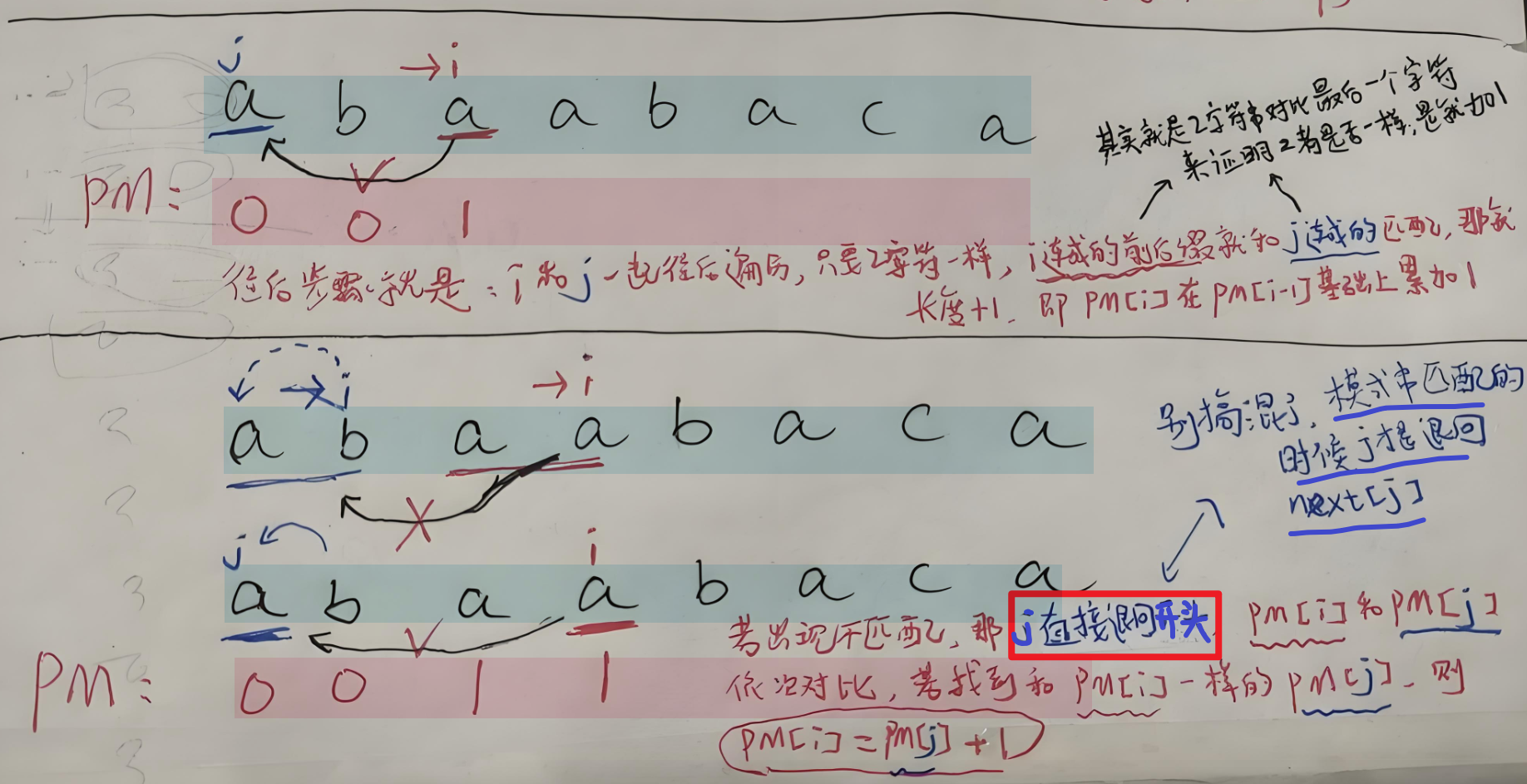
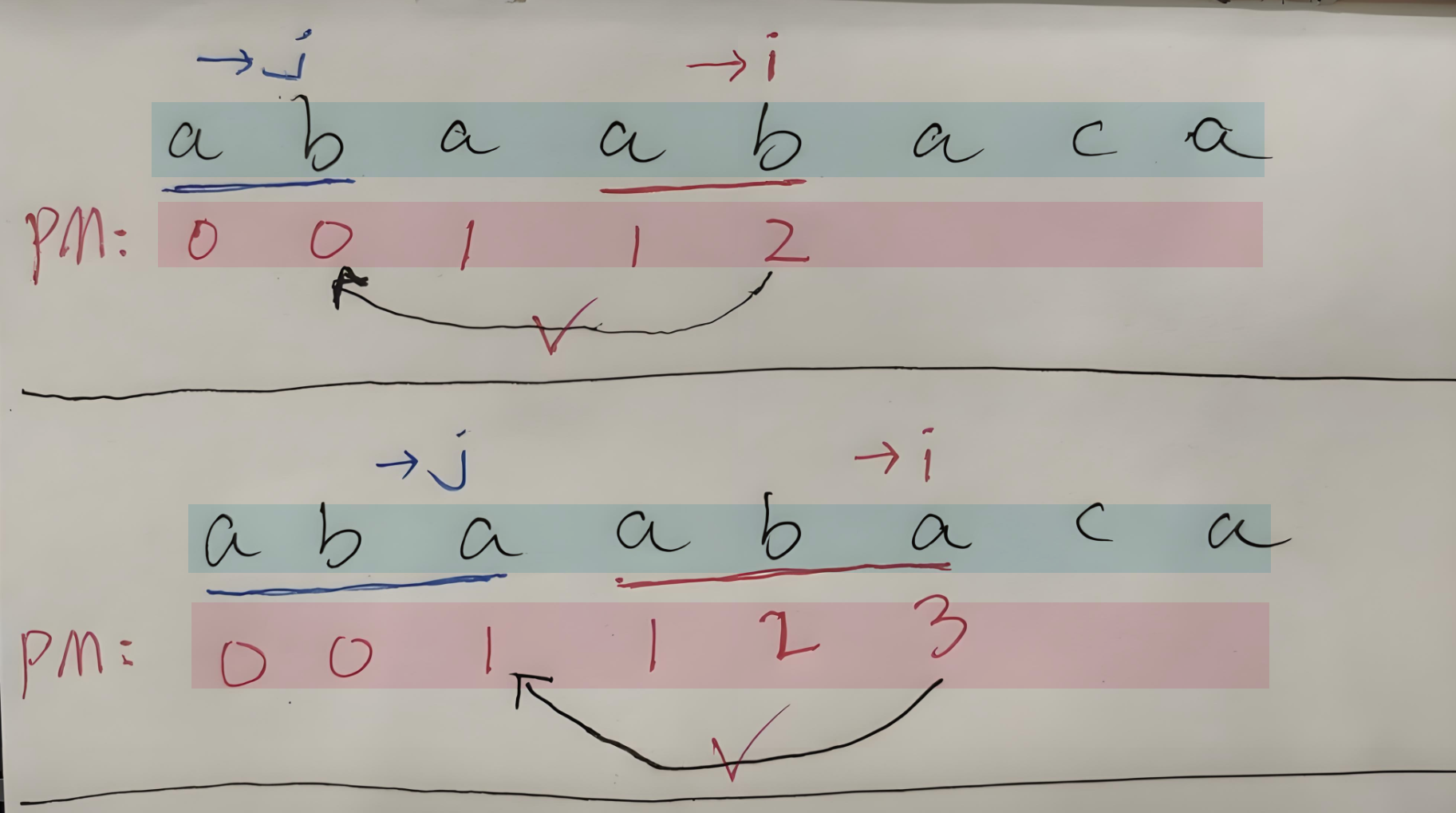
- 【第三步】:接下来【指针 j:指向第1位】、【指针 i:指向第3位】,它两开始正常同步往后遍历
- 【如果 PM[i] == PM[j]】:那么i连起来的字符串和j连起来的字符串一直一样,那就【PM[i] = PM[i-1]+1,统计相同最长前后缀长度】就行,也就是一直累加
- 【如果 PM[i] != PM[j]】:那么**【i 不要动!!】**,【指针 j 一步步往回遍历】
- 直到【指针 j 】找到【PM[i] == PM[j]】的字符,那么这个字符对应的PM是什么值,PM[i]就等于它+1,即【PM[i] = PM[j] + 1】
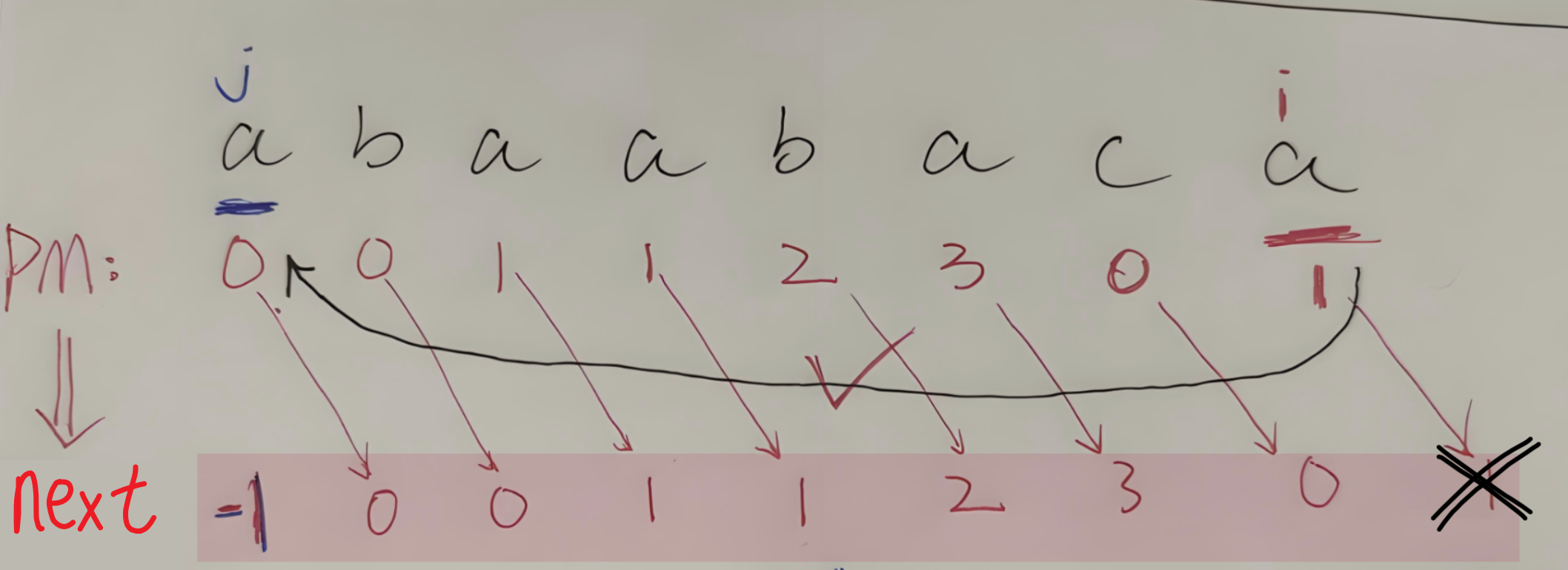
- 3、得出了【PM数组】后,再变两步就可以得到【next数组】了:
- 首先:把PM整体右移1位,第一位写-1
- 最后:整体每一位都+1,得到next数组(最后一位记得舍去就行了)
- 别问为什么,我有点懒得剖析它的原理了。。。老子只是考试狗而已
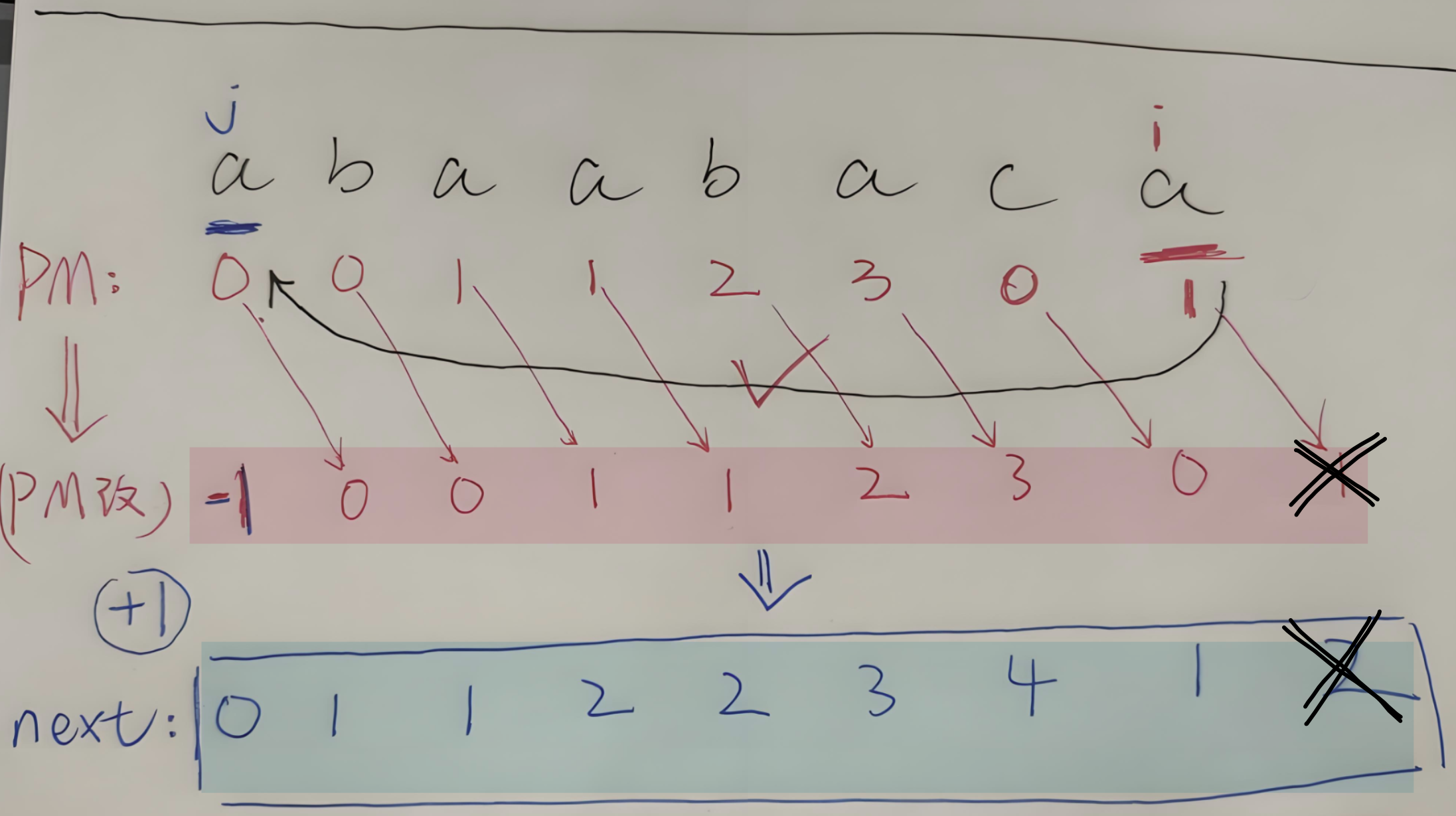
- 另外我这是为了写清楚给大家看,考试做题大家画一个数列在上面涂涂改改就行了,别像我这样写这么清晰的步骤
- 【另外】上面是字符串以【1为开头】的情况,如果是以【0为开头】的话,那PM转化成【next数组】时只需要【右移 + 开头补上-1】到这一步就够了!!!
3、KMP优化算法
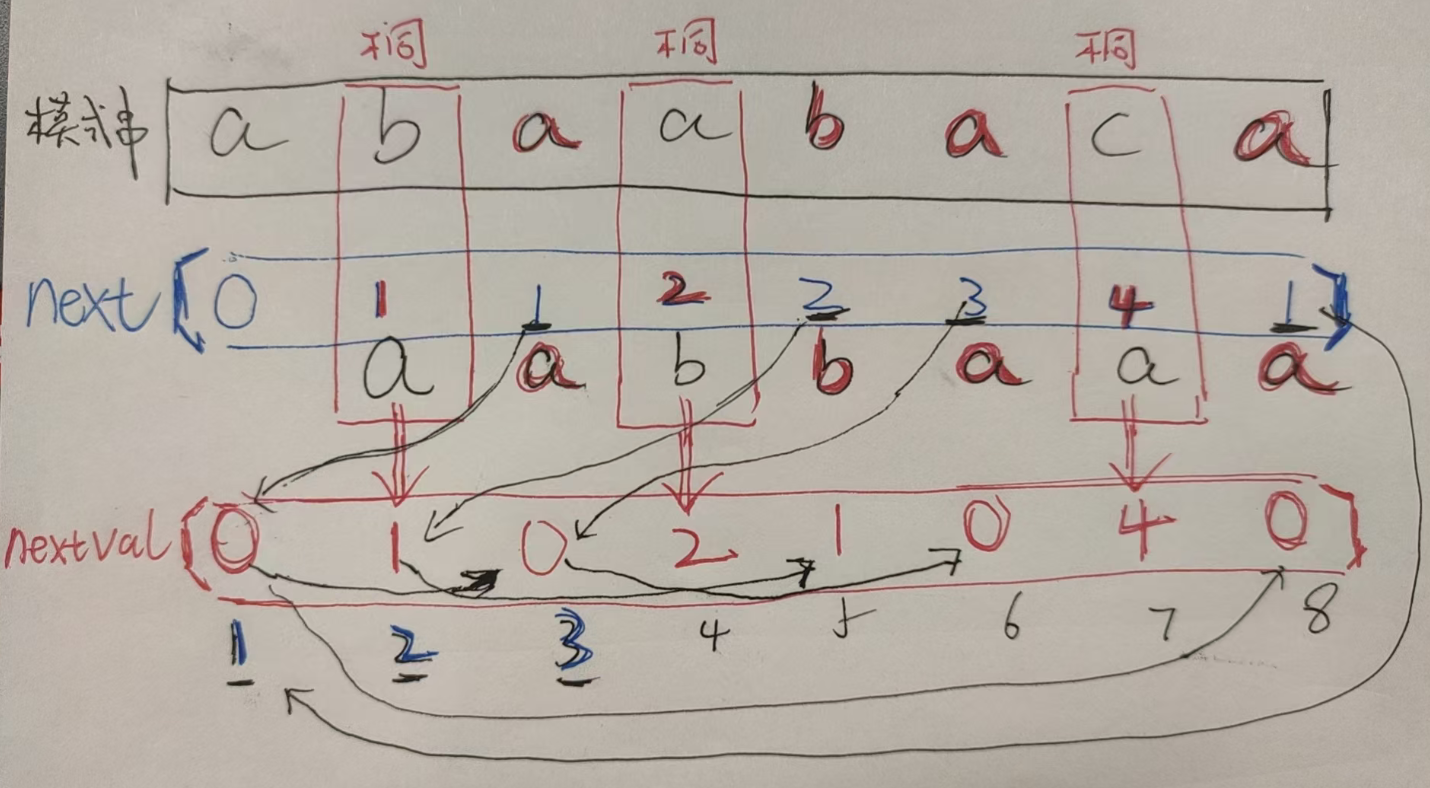
那么还有一种【next数组】Pro升级星耀版!!!------------【nextval数组】!!!
(【nextval数组】 也叫**【修正后的next数组】**)
我们需要知道原理吗?不需要!!写代码用不上!考试狗应试教育更用不上!!!
所以直接讲步骤怎么求得【nextval数组】:
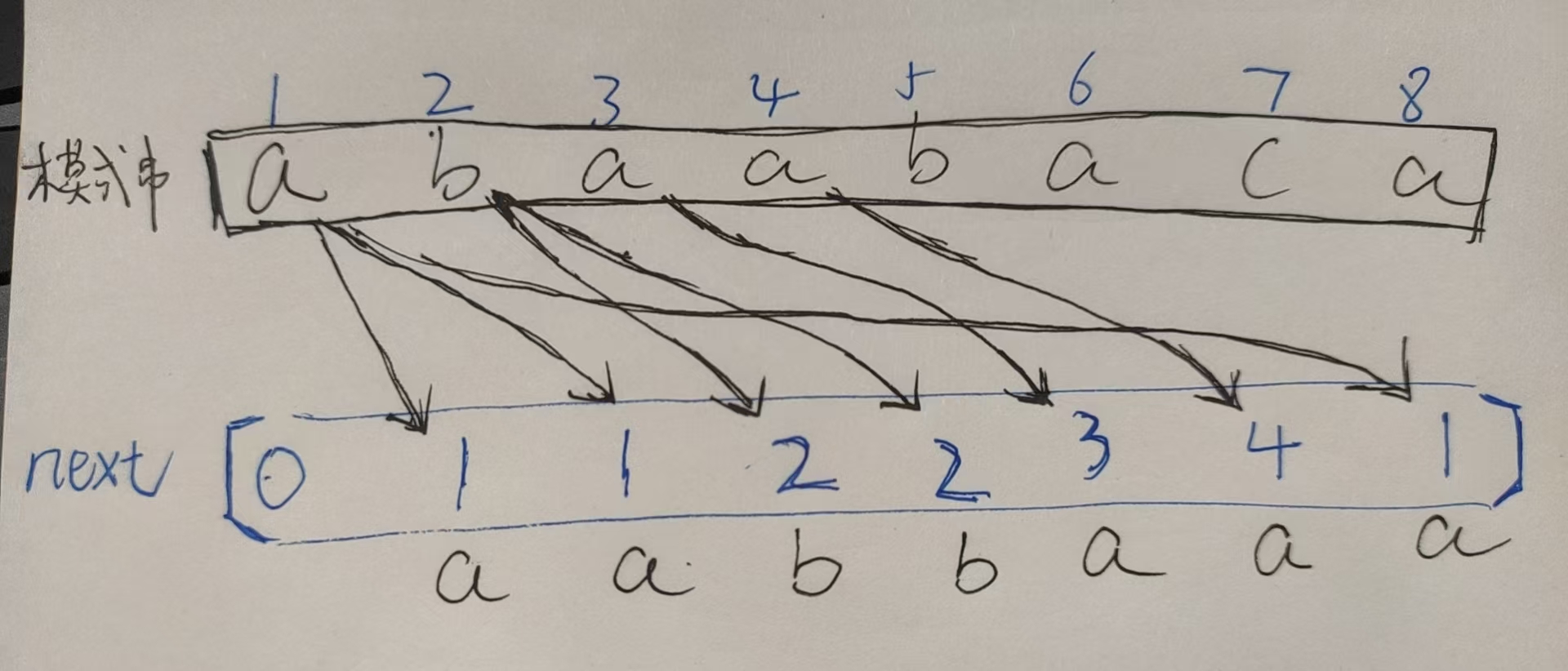
- 【第一步】:把刚刚求出的【next数组】抄在模式串下
- 然后给模式串【列序号(从1开始)】
- 然后在【next数组下】把**【每个值】对应的是【模式串的哪个序号的字符】** 列在下面,得出一个**【新的字符串(第1位不用写,空着)】**
- 【第二步】:然后把【新字符串】个【模式串对比】
- 从【新字符串】第2位开始,找出所有**【和模式串不一样的字符】!!!再三强调!!!是【不一样的】**!!!!
- 直接把不一样的这些字符对应的**【next数组的值】照抄到下面,作为【nextval】当前位的值**
- 然后**【nextval数组】的【第1位】**依旧跟【next数组】一样,默认是0
- 然后【新字符串】里剩下【和模式串一样的字符位】,我们根据上面【 next[i] 】找到【 nextval[ next[i] ] 】,就是【next[i]的值】
- 即**【 next[i] = nextval[ next[i] ] 】**!!!!!!!!!
- 而且强调,【nextval数组】也是从1开始
【例题】
未完待续。。。。。。。