在实际通信过程中，如在卫星通信、深空通信以及微波通信等系统中，信号的发射机与接收机之间往往存在着高速相对运动，此时会使进入接收端的信号存在较大的多普勒频移。
Costas 环在小频偏下能够比较精确地获取信号的同步载波，但其环路捕获带宽较窄，当信号的载波频偏一旦超出环路的捕获范围，系统的解调性能会急剧恶化。
因此对于高动态系统中的QPSK信号，对其进行频偏估计非常必要。
频偏估计的目的是通过对高动态信号进行变换处理，提取出其载波频偏信息，将估计结果导入本地振荡器，使其产生的信号与接收信号的频率差值处在较小范围内，以便锁相环可以完成捕获。
常用的频偏估计方法有最大似然法、差分频偏估计法和快速傅里叶变换(FFT)估计法等，其中FFT 频偏估计算法因结构易于实现、快速、准确度高、受噪声影响小等优点，被广泛应用于各类工程项目中。
频偏估计辅助Costa 环载波同步的解调系统如下图所示
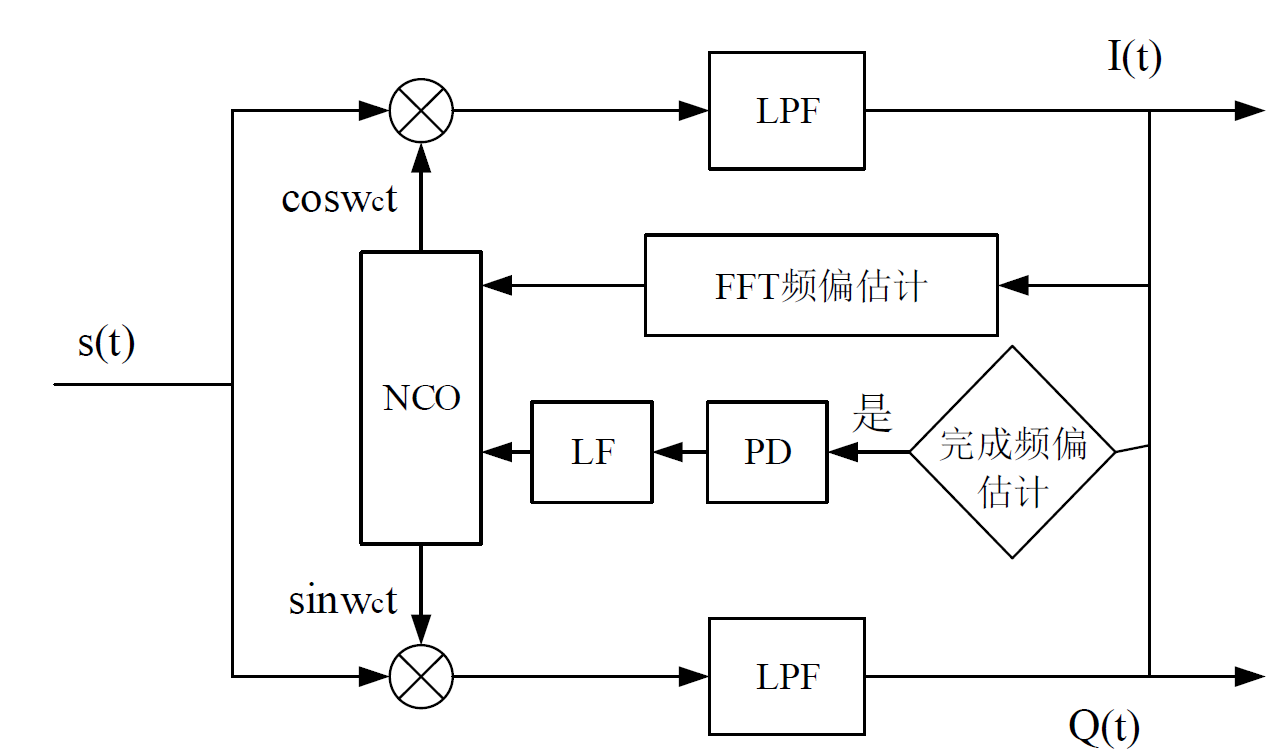
接收信号s(t)与本地数控振荡器产生的信号进行混频和低通滤波之后，得到带有多普勒频偏分量的I(t)、Q(t)两路正交信号。
对这两路正交分量先进行FFT 频偏估计，得到对多普勒频偏的粗略估计值，并将估计结果送给极性Costas 环的数控振荡器(NCO)模块，改变其输出信号的频率。
然后将之前得到的两路信号送入极性Costas 环，对剩余的频偏和相位差进行校正，完成整个的载波同步过程。
FFT 进行频偏估计的基本思想是当对接收信号进行快速傅里叶变换后，对其离散频谱图进行分析，可以在一定精度下得到被估计信号的频率大小。
使用FFT 进行频偏估计无须辅助数据，且当输入信号的信噪比大于某个门限值时，估计结果的误差精度只会受频偏检测设计的参数影响，而与输入信号的信噪比无关。
设进入接收端的QPSK 信号载波频偏大小为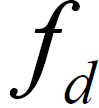
,系统采样时钟的大小为
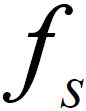,经过混频滤波之后输出的两路正交的信号为I(t)、Q(t)，对其以符号间隔
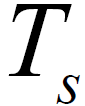的S 倍
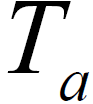(S 为正整数)进行抽取后可表示为：
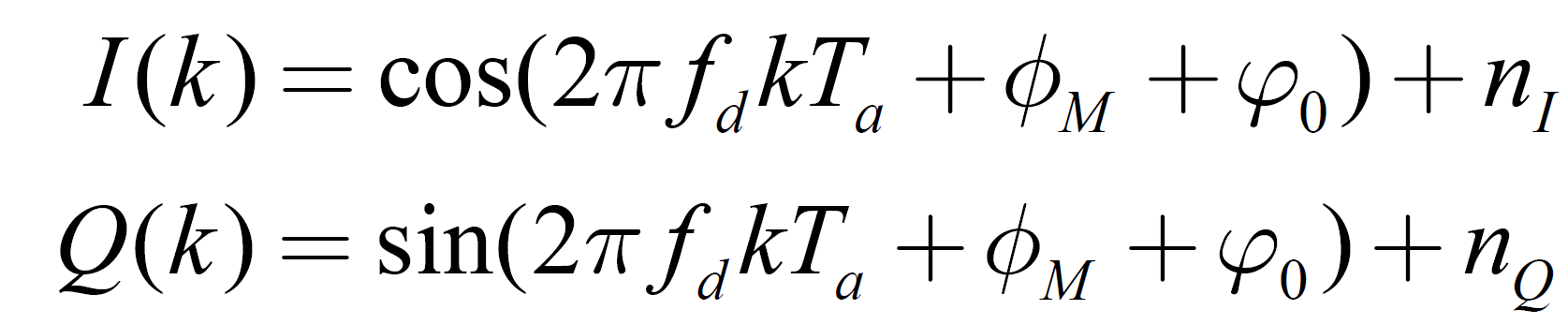
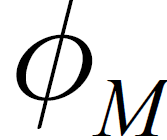为载波调制信息，
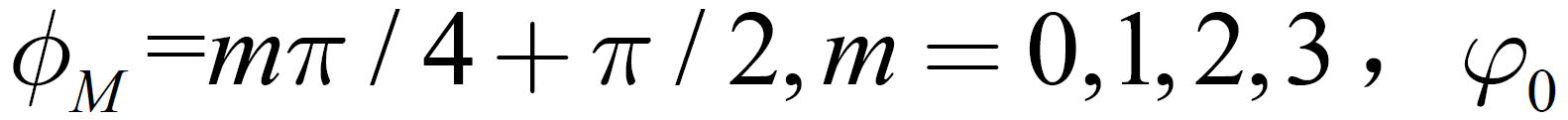为载波初始相位，
分别为 IQ支路上的高斯噪声分量。将I (k)和Q(k)经过 Viterbio非线性变换可以得到：
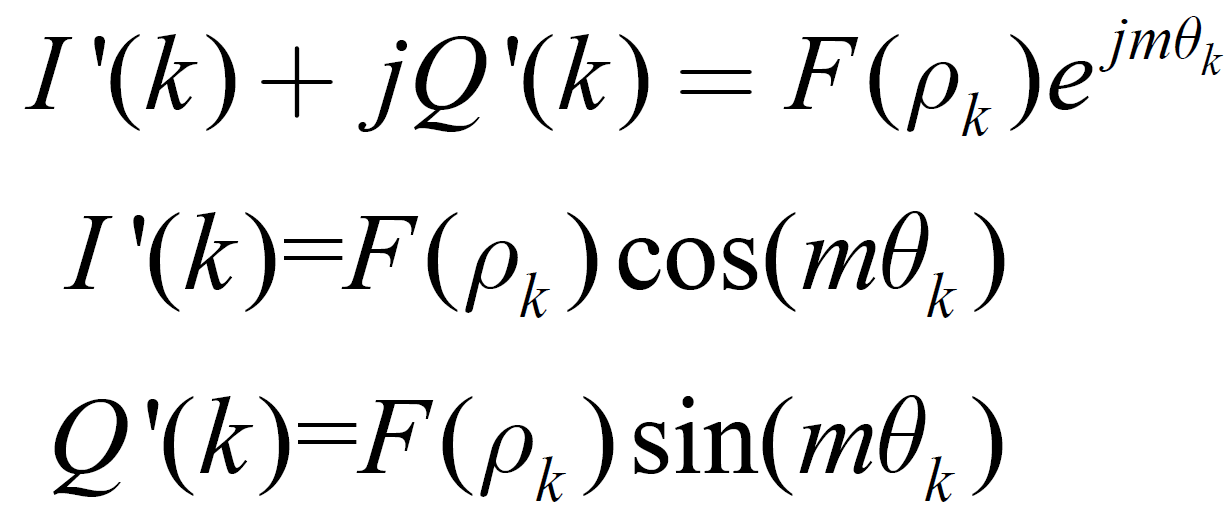
式中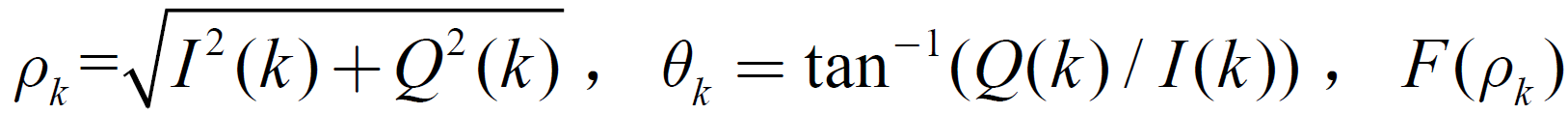
为对幅度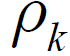
的非线性变换函数，可以有不同的形式。设
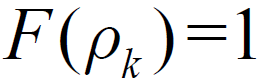，对于QPSK信号，m =4,则经过非线性变换后的输出为：
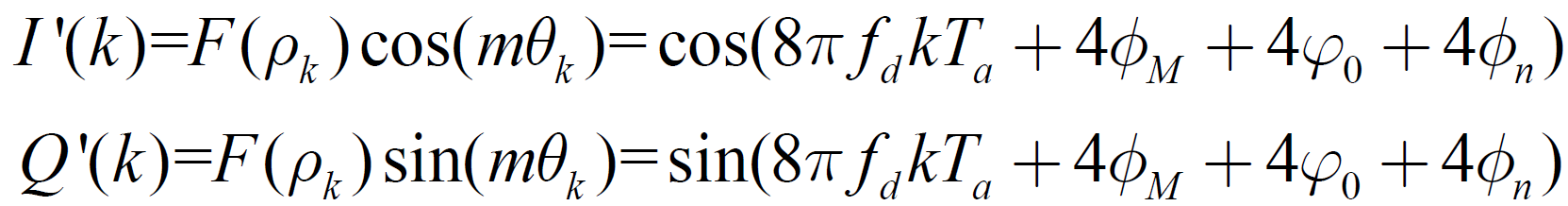
式中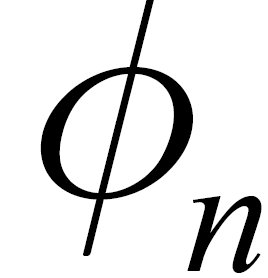
为高斯噪声分量经过非线性变换后得到的等效I、Q 相位角噪声。经过非线性变换后，消除了调制信息对载波相位的影响。非线性变换后的输出信号包含了4倍的载波频偏信息。对复数信号
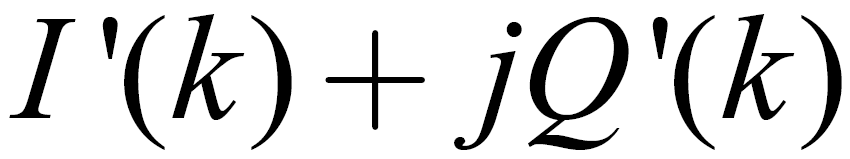进行快速傅里叶变换，则对频偏的最大似然估计值出现在其幅度频谱的峰值点上，可以得到
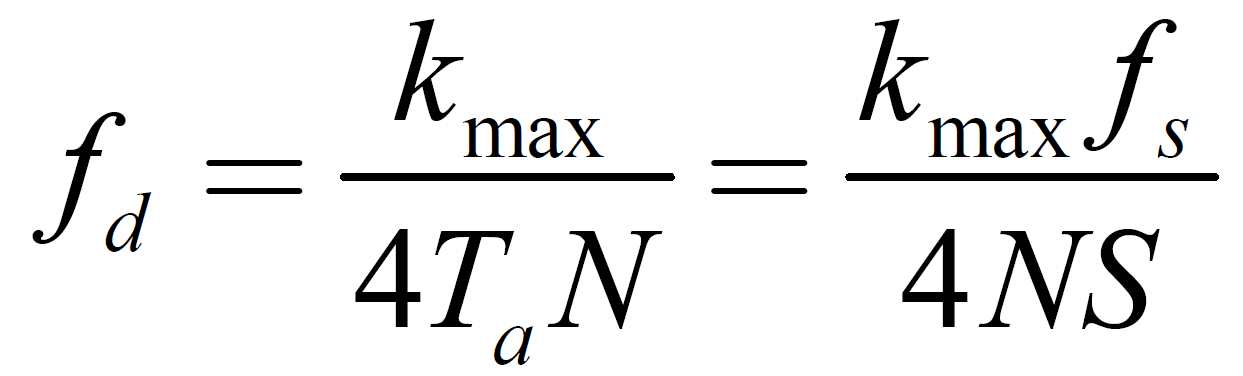
式中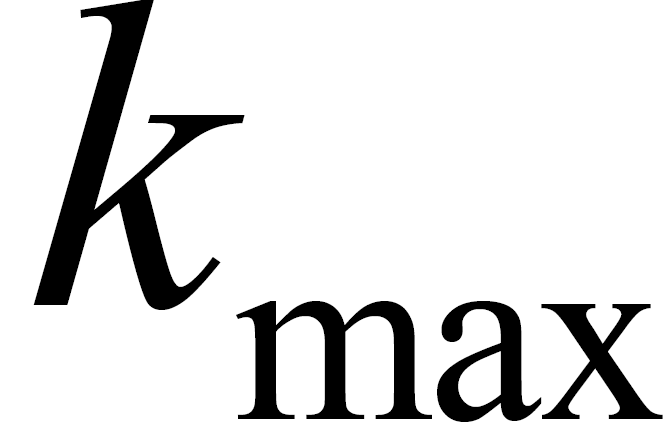
为信号经过FFT后幅频曲线最大峰值点的位置， N 为进行FFT 的点数。
可知，载波频偏的估计值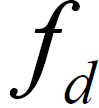与系统的采样频率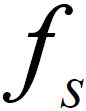成正比，与FFT点数N 和抽取倍数S 成反比。相对于采样频率的频偏估计精度分辨率为1/ 4NS ，由于对信号的采样
要满足奈奎斯特定理，故最大载波频偏的估计范围为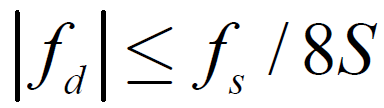
。如果要提高对载波频偏估计的精度，可通过增加进行FFT的点数N或者增加抽取倍数S 来实现。