DES对称加密算法
一、DES算法原理
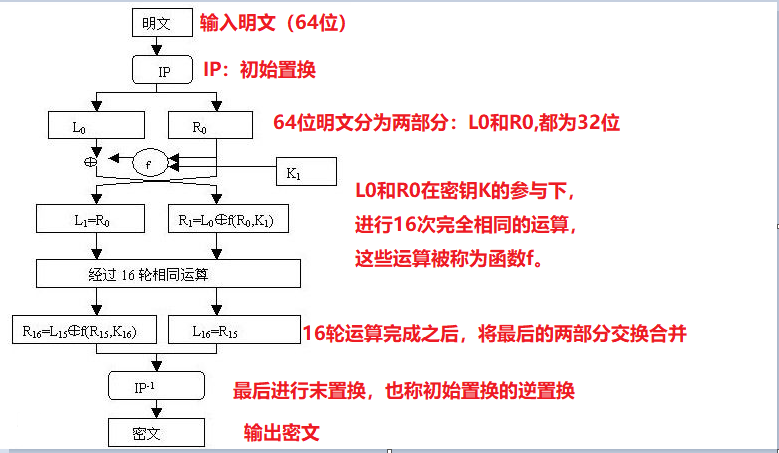
算法流程:
-
初始置换(IP置换):将输入的64位明文块进行置换和重新排列,生成新的64位数据块。
-
加密轮次:DES加密算法共有16个轮次,每个轮次都包括四个步骤:
-
将64位数据块分为左右两个32位块。
-
右侧32位块作为输入,经过扩展、异或、置换等操作生成一个48位的数据块。这个48位的数据块被称为"轮密钥",它是根据加密算法的主密钥生成的子密钥。
-
将左侧32位块和轮密钥进行异或运算,结果作为新的右侧32位块。
-
将右侧32位块与原来的左侧32位块进行连接,生成一个新的64位数据块,作为下一轮的输入。
-
-
末置换(FP置换):在最后一个轮次完成后,将经过加密的数据块进行置换和重新排列,得到加密后的64位密文。
算法原理:
-
PC1(密钥置换选择 1) :将 64 位原始密钥去除 8 位校验位,得到 56 位有效密钥,并调整位顺序。
-
PC2(密钥置换选择 2) :将 56 位密钥进一步置换为 48 位,生成每轮的子密钥。
-
IP(初始置换) :对 64 位明文分组进行初始位重排,打破明文原始位顺序。
-
IP_INV(逆初始置换) :与 IP 互为逆作,用于加密最后一步,还原位顺序。
-
E(扩展置换) :将 32 位数据扩展为 48 位,使数据长度与子密钥长度匹配
-
P(P 盒置换) :对 S 盒输出的 32 位数据进行位重排
-
S_BOXES(S 盒) :8 个 4×16 的非线性替代盒,将 6 位输入转换为 4 位输出
对称性数学验证(以 第 2 轮为例)
以 2 轮 Feistel 迭代为例,可直观验证解密的正确性:
-
加密过程:(加密输出)。
-
解密过程(输入,子密钥顺序):第 1 轮解密(用):,(异或抵消轮函数)。第 2 轮解密(用):,(最终还原)。
通过数学推导可见,反向使用子密钥可完全还原原始数据,证明了 DES 加解密的对称性。
二、DES 算法的弱密钥与安全性
- 弱密钥(Weak Keys)
DES 存在 4 个弱密钥,其特点是 "加密与解密等价"(),且 "加密两次还原明文"(),核心原因是弱密钥生成的 16 轮子密钥完全相同。4 个弱密钥(64 位,十六进制):
-
0000000000000000 -
FFFFFFFFFFFFFFFF -
00000000FFFFFFFFFFFFFFFF -
FFFFFFFFFFFFFFFF00000000
- 半弱密钥(Semi-weak Keys)
半弱密钥成对存在(共 6 对),特点是 "用 K1 加密后再用 K2 加密,还原明文"(),核心原因是两对密钥生成的子密钥互为补集。经典半弱密钥对(十六进制):
-
0101010101010101 与 FEFEFEFEFEFEFEFE -
1F1F1F1F0E0E0E0E 与 E0E0E0E0F1F1F1F1 -
01FE01FE01FE01FE 与 FE01FE01FE01FE01 -
1FE01FE00EF10EF1 与 E01FE01FF10EF10E -
01E001E001F101F1 与 E001E001F101F101 -
1FFE1FFE0EFE0EFE 与 FE1FFE1FFE0EFE0E
三、DES算法代码实现
"""
请使用编程语言实现对称加密算法DES(语言不限)
要求:
论述DES算法的原理及实现过程
请给出DES算法弱密钥,并通过程序验证弱密钥的危害
编程语言不限
"""
import sys
from typing import List, Tuple
# DES常量定义
# 密钥置换选择1矩阵
PC1 = [
57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4
]
# 密钥置换选择2矩阵
PC2 = [
14, 17, 11, 24, 1, 5, 3, 28,
15, 6, 21, 10, 23, 19, 12, 4,
26, 8, 16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55, 30, 40,
51, 45, 33, 48, 44, 49, 39, 56,
34, 53, 46, 42, 50, 36, 29, 32
]
# 加密扩展置换矩阵
E = [
32, 1, 2, 3, 4, 5, 4, 5,
6, 7, 8, 9, 8, 9, 10, 11,
12, 13, 12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21, 20, 21,
22, 23, 24, 25, 24, 25, 26, 27,
28, 29, 28, 29, 30, 31, 32, 1
]
# P盒置换矩阵
P = [
16, 7, 20, 21, 29, 12, 28, 17,
1, 15, 23, 26, 5, 18, 31, 10,
2, 8, 24, 14, 32, 27, 3, 9,
19, 13, 30, 6, 22, 11, 4, 25
]
# S盒置换矩阵
S_BOXES = [
# S1
[
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]
],
# S2
[
[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
[3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
[0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]
],
# S3
[
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
[1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]
],
# S4
[
[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
[3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14]
],
# S5
[
[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
[4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]
],
# S6
[
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
[9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
[4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]
],
# S7
[
[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
[1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
[6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]
],
# S8
[
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
[1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
[7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
[2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]
]
]
# 初始置换矩阵
IP = [
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7
]
# 初始置换逆矩阵
IP_INV = [
40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25
]
# 循环左移位数
SHIFT_SCHEDULE = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
# 根据置换表对数据块进行置换
def permute(block: int, table: List[int], n: int) -> int:
"""根据置换表对数据块进行置换"""
result = 0
for i, pos in enumerate(table):
bit = (block >> (n - pos)) & 1
result |= (bit << (len(table) - 1 - i))
return result
def generate_subkeys(key: int) -> List[int]:
"""从64位密钥生成16个48位子密钥"""
# 密钥置换1 (PC1),丢弃8个奇偶校验位
key_56 = permute(key, PC1, 64)
# 分为C0和D0
C = (key_56 >> 28) & 0x0FFFFFFF
D = key_56 & 0x0FFFFFFF
subkeys = []
for i in range(16):
# 循环左移
shift = SHIFT_SCHEDULE[i]
C = ((C << shift) | (C >> (28 - shift))) & 0x0FFFFFFF
D = ((D << shift) | (D >> (28 - shift))) & 0x0FFFFFFF
# 合并并应用PC2置换
CD = (C << 28) | D
subkey = permute(CD, PC2, 56)
subkeys.append(subkey)
return subkeys
def feistel(R: int, subkey: int) -> int:
"""Feistel函数"""
# 扩展置换
expanded = permute(R, E, 32)
# 与子密钥异或
xored = expanded ^ subkey
# S盒替代
s_output = 0
for i in range(8):
block = (xored >> (42 - i * 6)) & 0x3F
# row = ((block >> 5) << 1) | (block & 0x01)
# col = (block >> 1) & 0x0F
row = ((block & 0x20) >> 4) | (block & 0x01)
col = (block >> 1) & 0x0F
val = S_BOXES[i][row][col]
s_output |= (val << (28 - i * 4))
# P盒置换
return permute(s_output, P, 32)
def des_block(block: int, subkeys: List[int], encrypt: bool = True) -> int:
"""加密或解密单个64位数据块"""
# 初始置换
block = permute(block, IP, 64)
# 分为左右两部分
L = (block >> 32) & 0xFFFFFFFF
R = block & 0xFFFFFFFF
# 16轮Feistel网络
for i in range(16):
round_key = subkeys[i] if encrypt else subkeys[15 - i]
new_L = R
new_R = L ^ feistel(R, round_key)
L, R = new_L, new_R
# 合并左右部分
combined = (R << 32) | L
# 逆初始置换
return permute(combined, IP_INV, 64)
def pkcs7_pad(data: bytes, block_size: int = 8) -> bytes:
"""PKCS#7填充"""
pad_len = block_size - (len(data) % block_size)
return data + bytes([pad_len] * pad_len)
def pkcs7_unpad(data: bytes) -> bytes:
"""去除PKCS#7填充"""
pad_len = data[-1]
if pad_len < 1 or pad_len > 8:
raise ValueError("Invalid padding")
for b in data[-pad_len:]:
if b != pad_len:
raise ValueError("Invalid padding")
return data[:-pad_len]
# 将8字节转换为64位整数
def bytes_to_block(b: bytes) -> int:
"""将8字节转换为64位整数"""
return int.from_bytes(b, byteorder='big')
def block_to_bytes(block: int) -> bytes:
"""将64位整数转换为8字节"""
return block.to_bytes(8, byteorder='big')
def des_encrypt(key: bytes, plaintext: bytes) -> bytes:
"""DES加密函数"""
if len(key) != 8:
raise ValueError("Key must be 8 bytes (64 bits)")
key_int = bytes_to_block(key)
subkeys = generate_subkeys(key_int)
# 填充明文
padded = pkcs7_pad(plaintext)
ciphertext = []
for i in range(0, len(padded), 8):
block = bytes_to_block(padded[i:i + 8])
encrypted = des_block(block, subkeys, encrypt=True)
ciphertext.append(block_to_bytes(encrypted))
return b''.join(ciphertext)
def des_decrypt(key: bytes, ciphertext: bytes) -> bytes:
"""DES解密函数"""
if len(key) != 8:
raise ValueError("Key must be 8 bytes (64 bits)")
if len(ciphertext) % 8 != 0:
raise ValueError("Ciphertext length must be multiple of 8")
key_int = bytes_to_block(key)
subkeys = generate_subkeys(key_int)
plaintext = []
for i in range(0, len(ciphertext), 8):
block = bytes_to_block(ciphertext[i:i + 8])
decrypted = des_block(block, subkeys, encrypt=False)
plaintext.append(block_to_bytes(decrypted))
# 去除填充
return pkcs7_unpad(b''.join(plaintext))
def test_des():
"""测试DES加密解密功能"""
key = b'22922922'
plaintext = b'This is a test message for DES encryption.'
ciphertext = des_encrypt(key, plaintext)
decrypted = des_decrypt(key, ciphertext)
print("明文:", plaintext)
print("密钥:", key)
print("密文:", ciphertext.hex())
print("解密:", decrypted)
assert decrypted == plaintext, "Encryption/decryption failed"
def test_weak_keys():
"""测试DES弱密钥和半弱密钥"""
# 弱密钥(Weak Keys)
weak_keys = [
b'\x01\x01\x01\x01\x01\x01\x01\x01',
b'\xFE\xFE\xFE\xFE\xFE\xFE\xFE\xFE',
b'\xE0\xE0\xE0\xE0\xF1\xF1\xF1\xF1',
b'\x1F\x1F\x1F\x1F\x0E\x0E\x0E\x0E'
]
# 半弱密钥对(Semi-weak Key Pairs)
semiweak_pairs = [
(b'\x01\xFE\x01\xFE\x01\xFE\x01\xFE', b'\xFE\x01\xFE\x01\xFE\x01\xFE\x01'),
(b'\x1F\xE0\x1F\xE0\x0E\xF1\x0E\xF1', b'\xE0\x1F\xE0\x1F\xF1\x0E\xF1\x0E'),
(b'\x01\xE0\x01\xE0\x01\xF1\x01\xF1', b'\xE0\x01\xE0\x01\xF1\x01\xF1\x01'),
(b'\x1F\xFE\x1F\xFE\x0E\xFE\x0E\xFE', b'\xFE\x1F\xFE\x1F\xFE\x0E\xFE\x0E'),
(b'\x01\x1F\x01\x1F\x01\x0E\x01\x0E', b'\x1F\x01\x1F\x01\x0E\x01\x0E\x01'),
(b'\xE0\xFE\xE0\xFE\xF1\xFE\xF1\xFE', b'\xFE\xE0\xFE\xE0\xFE\xF1\xFE\xF1')
]
# 使用正好8字节的明文
plaintext_block = b'12345678'
print(f"\n弱密钥测试明文块: {plaintext_block.decode()}")
# ==== 测试弱密钥 ====
print("===== 弱密钥测试 =====")
for i, key in enumerate(weak_keys):
key_int = bytes_to_block(key)
subkeys = generate_subkeys(key_int)
block = bytes_to_block(plaintext_block)
encrypted = des_block(block, subkeys, encrypt=True)
double_encrypted = des_block(encrypted, subkeys, encrypt=True)
double_encrypted_bytes = block_to_bytes(double_encrypted)
print(f"弱密钥 #{i+1}: {key.hex()}")
if double_encrypted_bytes == plaintext_block:
print("✅ 弱密钥特性成立: 加密两次等于明文")
else:
print("❌ 弱密钥特性不成立")
# 验证解密
decrypted = des_block(encrypted, subkeys, encrypt=False)
if block_to_bytes(decrypted) == plaintext_block:
print("✅ 解密正确")
else:
print("❌ 解密失败")
print("\n===== 半弱密钥测试 =====")
for i, (key1, key2) in enumerate(semiweak_pairs):
key1_int = bytes_to_block(key1)
key2_int = bytes_to_block(key2)
subkeys1 = generate_subkeys(key1_int)
subkeys2 = generate_subkeys(key2_int)
block = bytes_to_block(plaintext_block)
# 半弱密钥特性测试:E_{K2}(E_{K1}(P)) = P
encrypted1 = des_block(block, subkeys1, encrypt=True) # K1加密
encrypted2 = des_block(encrypted1, subkeys2, encrypt=True) # K2加密
print(f"半弱密钥对 #{i + 1}:\n K1: {key1.hex()}\n K2: {key2.hex()}")
if block_to_bytes(encrypted2) == block_to_bytes(block):
print("✅ 半弱密钥特性成立: E_{K2}(E_{K1}(P)) = P")
else:
print("❌ 半弱密钥特性不成立: E_{K2}(E_{K1}(P)) != P")
if __name__ == "__main__":
test_des()
test_weak_keys()
