【MATLAB例程】基于USBL和DVL的线性回归误差补偿，对USBL和DVL导航数据进行相互补偿，提高定位精度，附代码下载链接

本文所展示的程序通过线性回归（Linear Regression）和基于方差的最优加权融合 的方法，对水下常用的两种导航传感器------**超短基线定位系统（USBL）和多普勒计程仪（DVL）**的测量数据进行相互补偿和优化，以提高水下定位的精度。

文章目录

程序要点
运行结果
MATLAB源代码

程序要点

程序旨在通过线性回归（Linear Regression）和加权融合 的方法，对水下常用的两种导航传感器------**超短基线定位系统（USBL）和多普勒计程仪（DVL）**的测量数据进行相互补偿和优化，以显著提高水下定位的精度。

主要功能点：

真实轨迹生成与传感器数据模拟：
- 模拟一条圆形加直线的复杂真实轨迹，作为真值（Ground Truth）。
- 根据传感器特性，分别生成带有误差的USBL和DVL测量数据。
- USBL误差模型 ：包含较大的随机噪声、系统偏差 和尺度误差（模拟声学多径和传感器安装误差）。
- DVL误差模型 ：包含随机噪声、累积漂移 （积分误差）和尺度误差。
数据补偿：
- USBL补偿 ：利用DVL数据（经过平滑处理以减少噪声）作为参考，通过线性回归模型校正USBL的系统偏差 和尺度误差。
- DVL补偿 ：利用USBL数据（经过强滤波以减少噪声）作为参考，通过拟合并去除DVL数据的线性累积漂移，然后进行微调。
卡尔曼滤波式融合（最优加权）：
- 在补偿后的USBL和DVL数据的基础上，通过计算各自的方差（不确定度） ，采用基于方差的最优加权方法进行融合，以得到最终的优化定位结果。
结果分析与可视化：
- 计算并打印原始数据、补偿后数据 和融合结果 的均值、标准差、RMSE、95%分位数等详细的定位误差统计特性。
- 计算USBL、DVL和融合结果相较于原始数据的误差改善率。
- 提供多组图表进行直观对比：
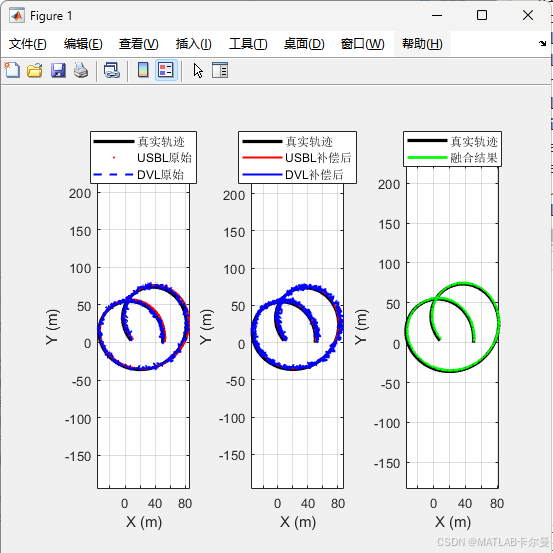
  - 原始轨迹、补偿后轨迹和融合轨迹的对比图。
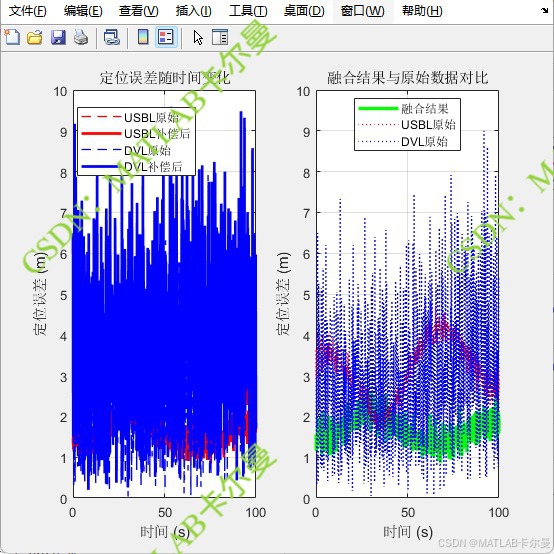
  - 定位误差随时间变化的曲线图。
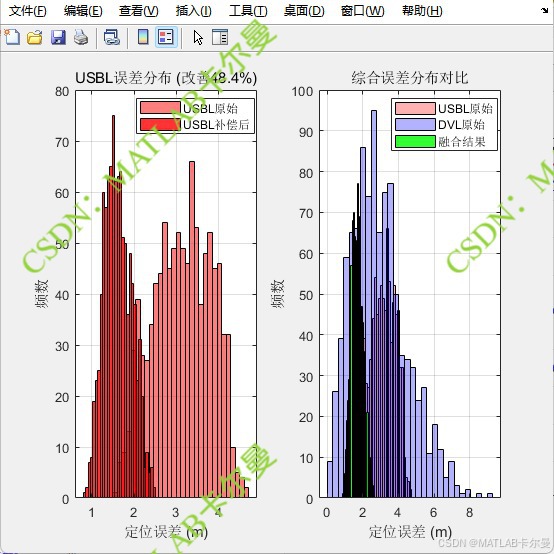
  - 误差分布的直方图。
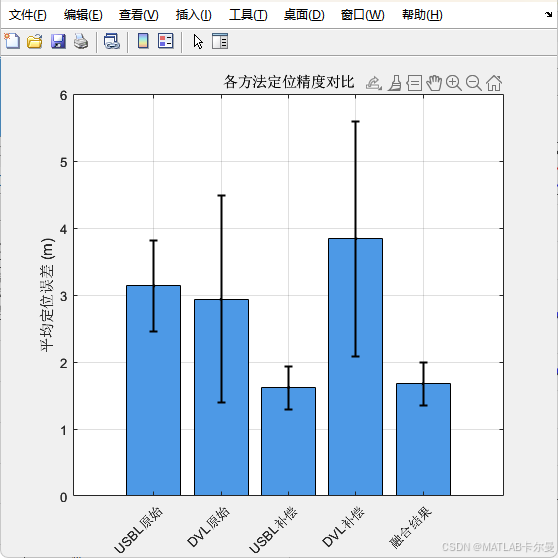
  - 各方法平均定位误差的柱状图。

适用场景：

水下潜水器（如AUV/ROV）的后处理导航 或实时导航算法验证。特别是在水下环境复杂，USBL易受多径影响（噪声大、有偏差），而DVL易产生累积漂移的场景下，用于提高系统的整体定位精度。

运行结果

轨迹对比：

误差对比：

误差分布情况：

误差均值与标准差图像：

MATLAB源代码

完整代码如下：

matlab 复制代码

%% USBL和DVL数据线性回归补偿程序
% 功能：对USBL和DVL导航数据进行相互补偿，提高定位精度
% 作者: matlabfilter
% 2025-10-12/Ver1

clear; close all; clc;
rng(0);
%%  参数设置
dt = 0.1;           % 采样时间间隔 (s)
t_total = 100;      % 总时间 (s)
t = 0:dt:t_total;   % 时间向量
N = length(t);      % 数据点数

%% 生成真实轨迹（圆形+直线）
omega = 0.1;        % 角速度
radius = 50;        % 圆半径
x_true = radius * cos(omega * t) + 0.5 * t;
y_true = radius * sin(omega * t) + 0.3 * t;

%% 生成USBL和DVL测量数据（符合实际传感器特性）
% USBL误差模型：较大随机噪声 + 系统偏差（受声学多径影响）
usbl_noise_scale = 0.2;

完整代码的下载链接：
https://download.csdn.net/download/callmeup/92114650

或前往专栏查看更多完整代码（粘贴到MATLAB空脚本中即可直接运行）：
https://blog.csdn.net/callmeup/article/details/153126168?spm=1011.2415.3001.5331

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者