近年来，大型语言模型（LLM）在数学推理、代码生成等复杂任务上取得了显著进展，其中强化学习（RL）的后训练（Post-Training）扮演了关键角色。然而，RL训练过程对数据批处理（batching）和提示（prompt）选择策略极为敏感，传统方法通常依赖高成本的生成采样（rollouts）或历史奖励字典，导致训练效率低下且容易偏离当前策略。
-
论文：Prompt Curriculum Learning for Efficient LLM Post-Training
本文提出了一种名为Prompt Curriculum Learning (PCL) 的轻量级强化学习算法，旨在通过动态选择"中等难度"的提示，显著提升LLM后训练的样本效率与收敛速度。PCL的核心创新在于引入一个在线学习的价值模型（value model），仅通过单次前向传播即可预测提示的难度，避免了传统方法中昂贵的多轮生成采样。论文通过系统性的实验验证了PCL在多个数学推理基准（如MATH、DeepScaleR）上的优越性，为高效RL训练提供了新的方法论。
研究动机与关键发现
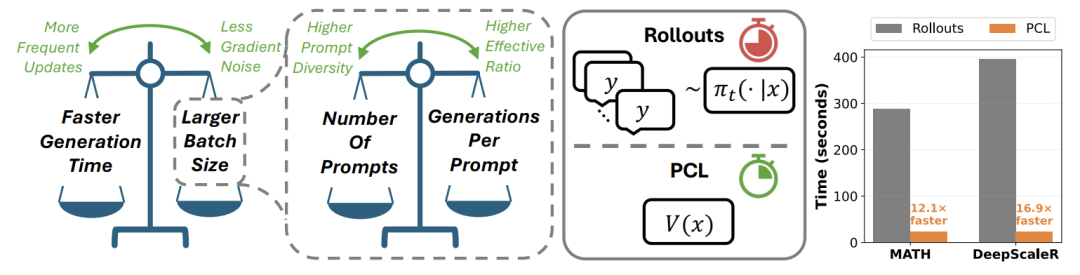
在RL训练中，如何选择"合适"的提示一直是个难题。太简单的提示无法提供有效的学习信号，太难的提示则可能导致梯度消失。论文首先通过大量实验（耗费约10万A100 GPU小时）揭示了两个关键现象：
- 批量大小（Batch Size）存在最优值：
-
当批量较小时，生成速度快但梯度噪声大；当批量过大时，生成时间线性增长，更新频率下降。
-
最优批量大小位于生成时间从亚线性增长转为线性增长的过渡点（约8K），此时能在梯度质量与更新频率间取得最佳平衡。
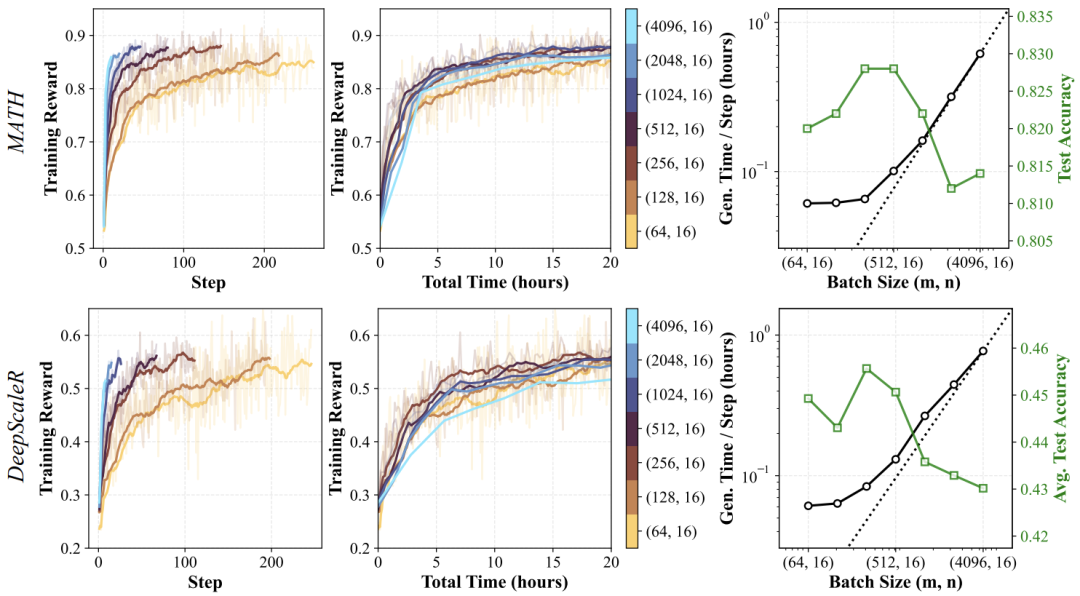不同批量配置下训练奖励随步骤与时间的变化，以及生成时间与测试准确率的关系
- 中等难度提示（p(x)≈0.5）最具学习价值：
-
当模型在某个提示上的正确率约为50%时，其梯度范数（gradient norm）和有效比率（effective ratio）最高，即大多数样本能贡献非零梯度信号。
-
相比之下，过于简单或困难的提示会导致梯度信号微弱，浪费计算资源。
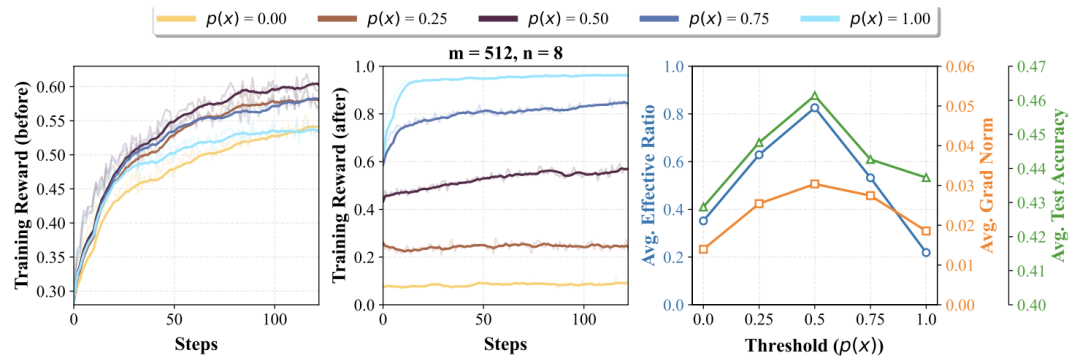
上图显示，当p(x)=0.5时，即使每个提示的生成数（n）较小，有效比率与测试准确率仍显著高于其他难度级别。
这些发现为PCL的设计提供了理论基础：通过聚焦中等难度提示，能以更少的样本实现更高效的训练。
PCL方法详解
PCL的核心理念是使用一个轻量级的价值模型（value model）来动态筛选中等难度的提示，避免传统方法中昂贵的多轮生成采样或离策略（off-policy）问题。其算法流程如下：
-
候选提示采样：每步从数据集中采样km个候选提示（k为超参数，默认4）。
-
难度预测：对每个提示x，通过价值模型V(x)预测其期望奖励（即估计p_π(x)）。
-
提示选择：选择预测值最接近目标阈值τ（默认0.5）的m个提示，构成当前批次。
-
策略更新：对每个选中提示生成n个响应，使用GRPO目标更新策略。
-
价值模型更新：利用生成的实际奖励，通过最小化预测误差更新价值模型：
该公式是价值模型的损失函数，目标是让预测值V(x)逼近实际的平均奖励。
关键设计优势：
-
效率高：价值模型仅需单次前向传播，远快于多轮生成（速度提升12-16倍）。
-
同策略（on-policy）：始终基于当前策略筛选提示，避免历史数据偏差。
-
自适应课程：随着策略改进，价值模型自动调整难度选择，实现渐进式学习。
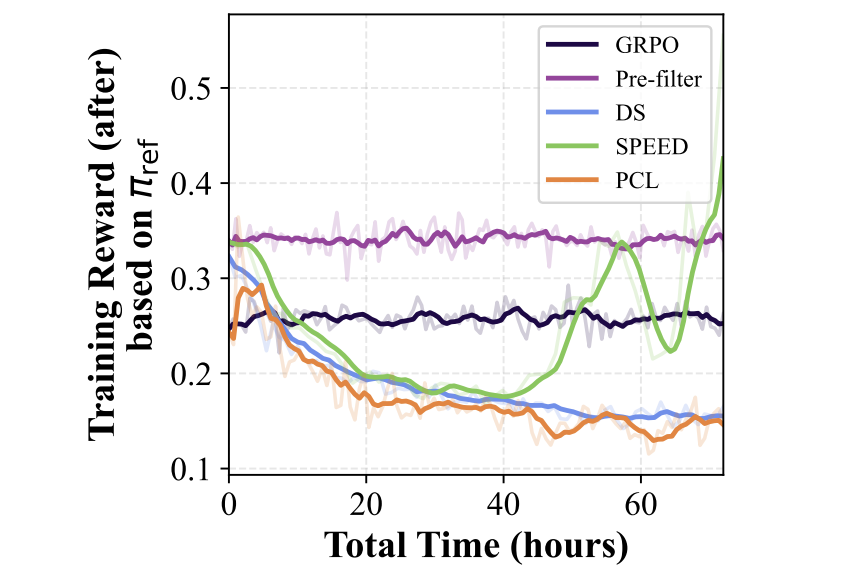
上图显示，尽管PCL的阈值τ固定为0.5，但随着训练进行，所选提示的实际难度逐渐增加，体现了"课程学习"的动态适应性。
实验设计与结果分析
论文在多个模型（Qwen3-1.7B/4B/8B-base, Llama3.2-3B-it）和数据集（MATH、DeepScaleR等）上验证PCL，并与五种基线方法对比：
-
GRPO：无提示过滤的标准方法。
-
Pre-filter：基于初始策略的静态过滤。
-
DS：动态采样，依赖多轮生成估计难度。
-
SPEED：DS的改进版，减少生成数但引入离策略问题。
-
GRESO：基于历史奖励字典的方法。
主要结果：
-
性能领先：在MATH上，PCL在所有模型上取得最高准确率（如Qwen3-8B达88.2%）；在DeepScaleR上平均准确率排名第一或第二。
-
时间效率：PCL在达到相同性能时，训练时间显著低于DS、SPEED等方法。
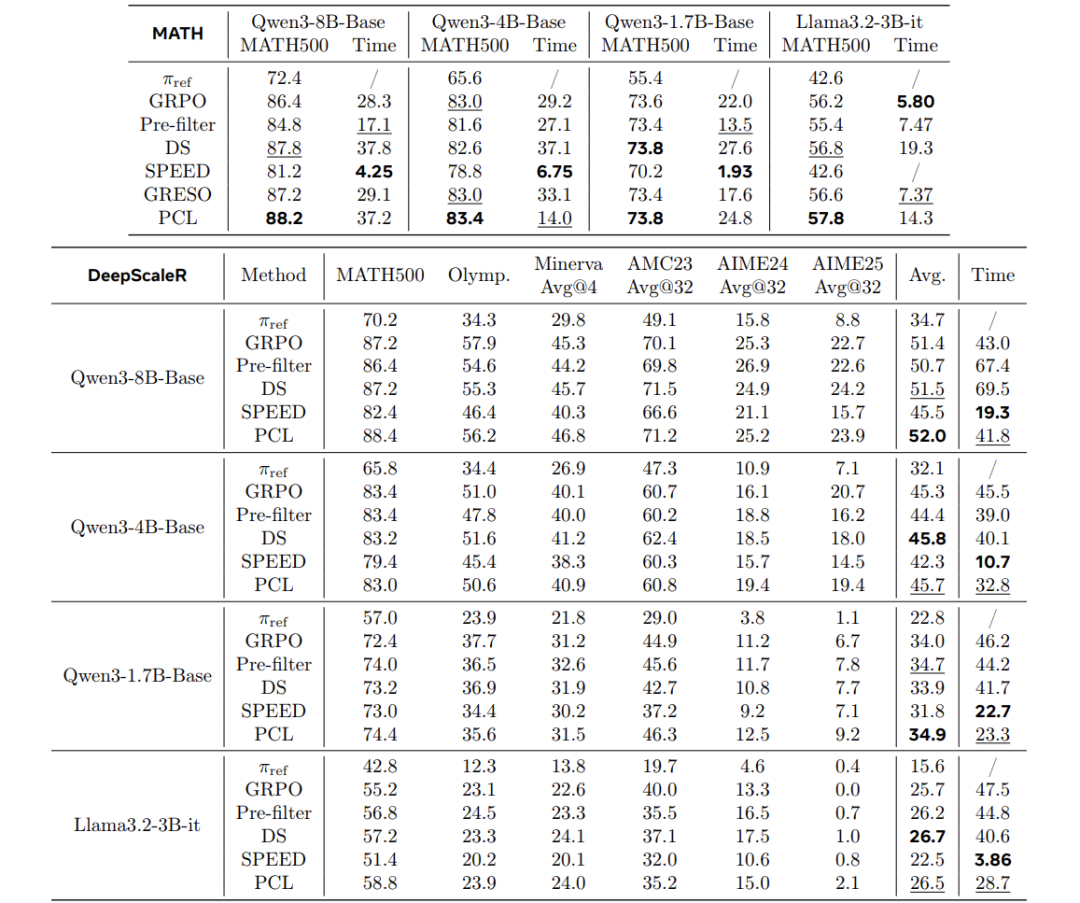各方法在MATH和DeepScaleR上的准确率与训练时间
深入分析：
-
有效比率与生成时间：PCL在保持高有效比率的同时，生成时间远低于DS和SPEED（见图6）。
-
价值模型准确性：PCL的价值模型预测精度相当于使用3个rollouts的估计，但速度快12.1-16.9倍。
-
阈值鲁棒性：当τ=0.5时，价值模型的预测精度最高，且与无过滤基线相当。
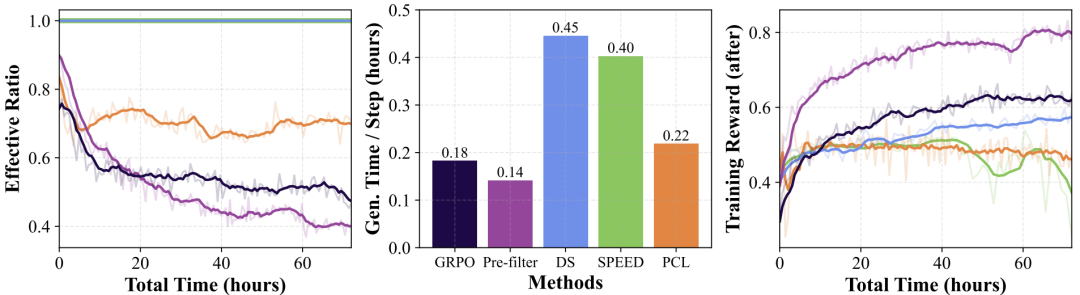图6
图6显示PCL的有效比率始终高于GRPO和Pre-filter，而生成时间低于DS和SPEED。
讨论与局限性
方法扩展性：
-
PCL可自然扩展至非二元奖励任务，只需调整价值模型的输出范围和阈值τ。
-
在数学推理等结构性强的任务中，提示级泛化假设成立，但在其他领域需进一步验证。
局限性：
-
纯粹同策略设置：未利用离线数据或回放缓冲区，可能限制泛化能力。
-
同步训练架构：未适配异步RL系统，未来需研究如何处理策略滞后问题。
-
有限上下文长度：实验最大长度为4096令牌，长上下文下的批量优化仍需探索。
-
短训练周期：实验仅运行2-3天，长期收敛行为未知。
结论
本文提出了Prompt Curriculum Learning (PCL) ，一种通过价值模型动态选择中等难度提示的高效RL算法。其核心贡献包括：
-
系统揭示了批量大小与提示难度对RL训练的关键影响。
-
设计了轻量级价值模型，避免了传统方法中的高成本rollouts与离策略问题。
-
在多个基准上验证了PCL在性能与效率上的优越性，为LLM后训练提供了新的解决方案。
PCL不仅提升了RL训练的样本效率，也为课程学习在LLM中的应用开辟了新路径。未来工作可探索其在更长上下文、异步训练及多模态任务中的潜力。
