Information
- Authors: Taoyang Qin, Ke-Jia CHEN, Zheng Liu
- Affiliations: Nanjing University of Posts and Telecommunications
Abstract
- 针对问题:图中存在重复的特征值,限制谱域GNN的能力
- 解决: 高维 sheaf Laplacian Matrix------对图的拓扑信息进行编码,同时提高不同特征值数量的上界
- Sheaf Laplacian Matrix 由 Normalized Graph Laplacian 的 block form 进行扰动获取
- 理论分析了添加 Pertubed Sheaf Laplacian(PSL) 之后的谱域 GNN 的表达能力
- 确立了特征值的 perturbation bounds
- 基于节点分类任务测试了模型能力
1. Introduction
- 此前工作多在设计线性变化解决特征值重复的问题,本文从 non-linear 的情景出发
2. Preliminaries
2.1 Spectral GNNs
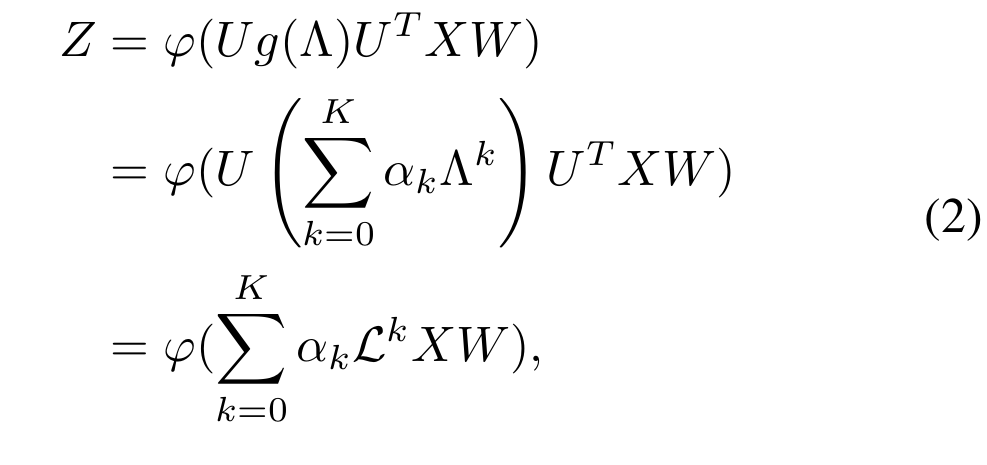
若 φ \varphi φ 为线性/非线性函数,对应的 GNN 也相应被称为 线性/非线性 spectral GNNs
2.2 Theory of Cellular Sheaves
Definition 2.1
无向图 G = ( V , E ) G=(V,E) G=(V,E) 上的 cellular sheaf ( G , F ) (G, \mathcal{F}) (G,F)定义为:
- 向量空间 F ( v ) \mathcal{F}(v) F(v): 对应每个节点
- 向量空间 F ( e ) \mathcal{F}(e) F(e): 对应每条边
- 线性映射 向量空间 F v ⊴ e \mathcal{F}_{v \unlhd e} Fv⊴e:对应每个邻接的节点-边对 v ⊴ e v\unlhd e v⊴e,将 F ( v ) \mathcal{F}(v) F(v) 的向量映射到 F ( e ) \mathcal{F}(e) F(e)
节点和边对应的向量空间称为 stalks,线性映射称为 restriction maps,这里令所有的stalks均为 R d \mathbb{R}^d Rd,restricion maps 均为正交映射; F v ⊴ e \mathcal{F}{v \unlhd e} Fv⊴e 和 F v ⊴ e T \mathcal{F}{v \unlhd e}^T Fv⊴eT 分别表示从 node/edge stalk 到 edge/node stalk 的映射,则有 F u ⊴ ( v , u ) T F v ⊴ ( v , u ) \mathcal{F}{u \unlhd (v,u)}^T\mathcal{F}{v \unlhd (v,u)} Fu⊴(v,u)TFv⊴(v,u)表示从 F v \mathcal{F}{v} Fv 到 F u \mathcal{F}{u} Fu 的映射
Definition 2.2
无向图 G G G 上的单个 sheaf 对应的 sheaf Laplacian matrix 是一个块矩阵 L F \mathcal{L}_{\mathcal{F}} LF
- 对角块为 L F , v v = ∑ v ⊴ e F v ⊴ e T F v ⊴ e \mathcal{L}{\mathcal{F},vv} = \sum{v\unlhd e} \mathcal{F}{v \unlhd e}^T\mathcal{F}{v \unlhd e} LF,vv=∑v⊴eFv⊴eTFv⊴e
- 非对角块为 L F , v u = − F v ⊴ e T F u ⊴ e \mathcal{L}{\mathcal{F},vu} =- \mathcal{F}{v \unlhd e}^T\mathcal{F}_{u \unlhd e} LF,vu=−Fv⊴eTFu⊴e
半正定矩阵,当 restriction maps 为 identity maps 时, sheaf Laplacian Matrix 即为 graph Laplacian matrix 的块形式
Definition 2.3
sheaf Laplacian matrxi 的 normalized form 为 L F ‾ = D − 1 / 2 L F D − 1 / 2 , D v = L F , v v \overline{\mathcal{L}{\mathcal{F}}}=D^{-1/2}\mathcal{L}{\mathcal{F}}D^{-1/2}, D_v=\mathcal{L}_{\mathcal{F},vv} LF=D−1/2LFD−1/2,Dv=LF,vv ,sheaf Laplacian matrix 的对角阵为 D = d i a g ( D 1 , . . . , D n ) D=diag(D_1,...,D_n) D=diag(D1,...,Dn)
3. Motivation
3.1 Limited Predictive Ability
Lemma 3.1.
若图拉普拉斯矩阵只有 k k k 个不同的特征值,线性谱域GNNs最多只能生成 k k k 个不同的 filter coefficients,因此最多只能生成最多 k k k 个不同元素的一维预测结果
Theorem 3.2.
若图拉普拉斯矩阵只有 k k k 个不同的特征值,若非线性实值函数 σ \sigma σ 满足 x ≠ 0 x \neq 0 x=0 则 σ ( x ) ≠ 0 \sigma(x)\neq 0 σ(x)=0,那么非线性谱域 GNNs最多只能生成 k k k 个不同的 filter coefficients,因此最多只能生成最多 k k k 个不同元素的一维预测结果
即便添加了非线性的激活函数,仍然无法提升预测能力
3.2 Loss of Frequency Components
若特征值存在重复,且对应的 filter function g ( λ ) g(\lambda) g(λ) 选取不佳的话,会将某些特征值对应的值设为0,造成对应的多个频率信号一起丢失
一个小例子:很多数据集中均会出现特征值 1 的重复,因此使用 GCN ( g ( λ ) = 1 − λ g(\lambda)=1-\lambda g(λ)=1−λ)时,如果不添加 self-loop,效果会差很多,添加之后特征值分布发生变化,丢失的 frequency component 会减少,进而提升模型表现
3.3 Restricted Frequency Processing Capability
重复的特征值会导致谱域 GNNs 的 g ( λ i ) g(\lambda_i) g(λi)出现重复,因此对不同的 X i ^ \hat{X_i} Xi^ 和 \\hat{X_j} 的处理也会变得一样,缺乏区分性
3.4 Why Perturbed Sheaf Laplacian
Sheaf Laplacian:提供更大的特征值取值范围,仍然保持半正定且在 [0,2] 区间内
Pertubed Sheaf Laplacian(PSL):
- restriction map 设为 identity matrix 的轻微修改
- 提高特征值的多样性
- 更接近图拉普拉斯矩阵,保留拓扑结构信息
4. Method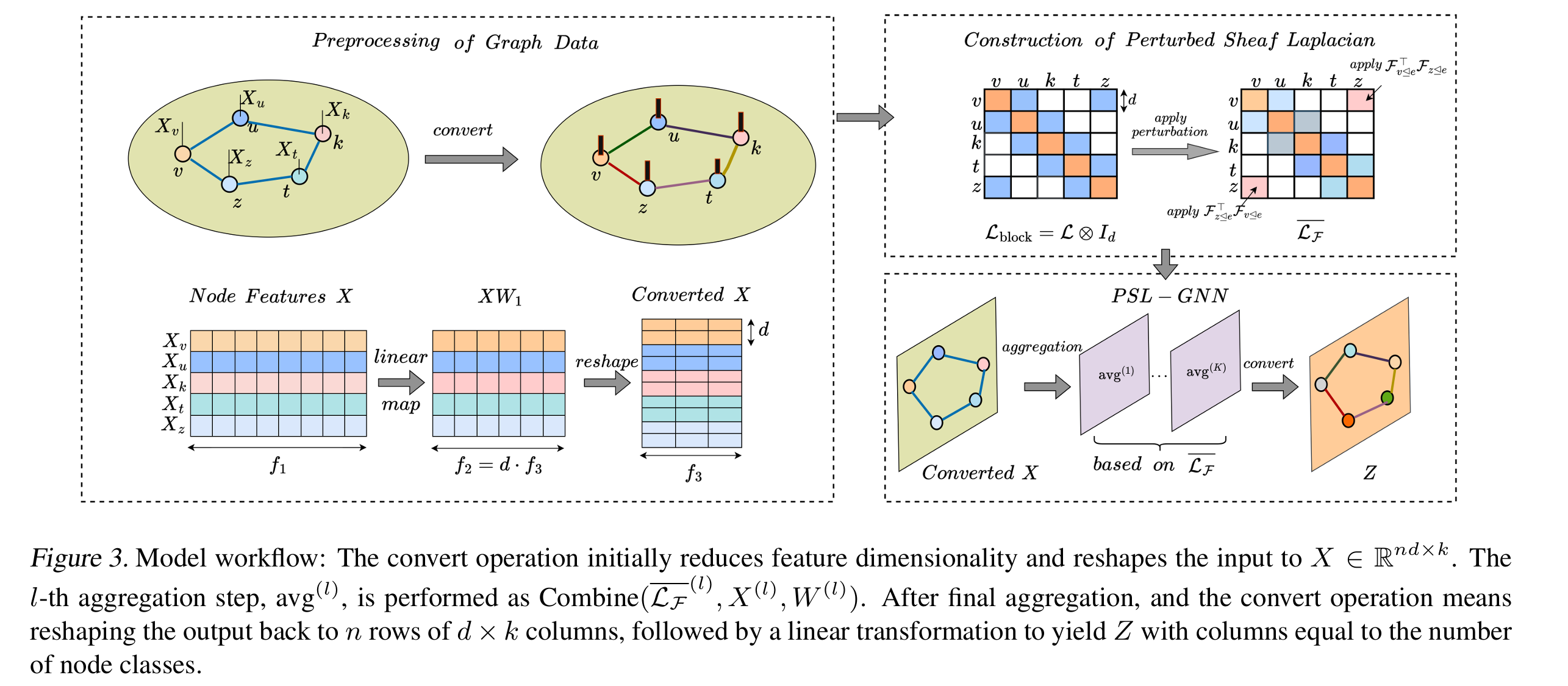
4.1 Preprocessing of Graph Data
将初始输入的图 X 0 ∈ R n × f 1 X_0\in \mathbb{R}^{n\times f_1} X0∈Rn×f1 转换成 sheaf Laplacian matrix L F ‾ ∈ R n d × n d \overline{\mathcal{L}_{\mathcal{F}}} \in \mathbb{R}^{nd\times nd} LF∈Rnd×nd:
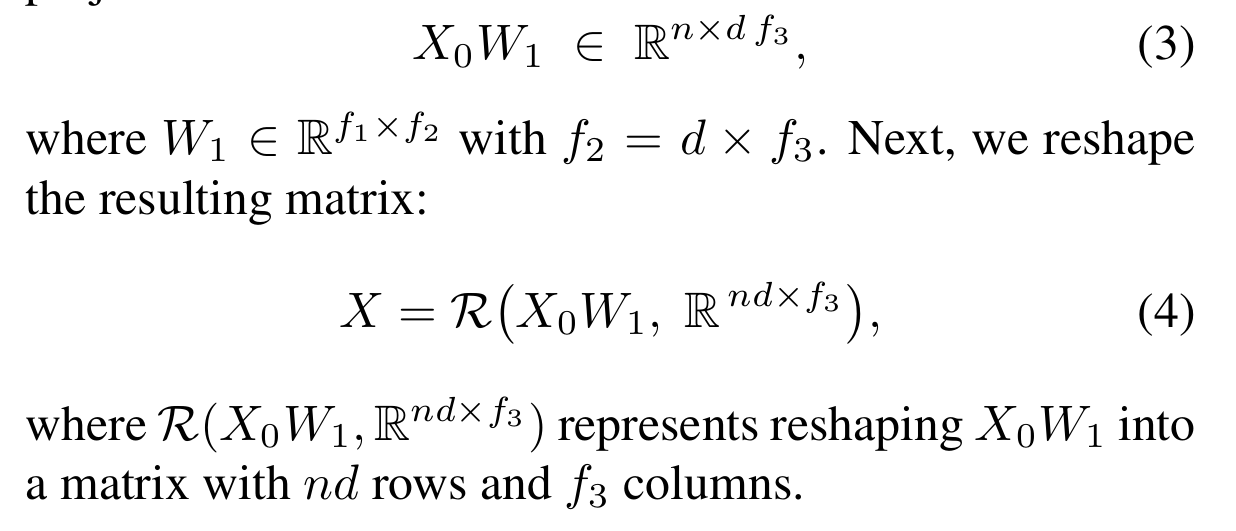
4.2 Construction of Perturbed Sheaf Laplacian
当restriction map不是 identity map 时, L F ‾ \overline{\mathcal{L}{\mathcal{F}}} LF 可视为对块形式的图拉普拉斯矩阵进行扰动之后的结果,对于每一个块 L b l o c k , i j \mathcal{L}{block,ij} Lblock,ij,施加相应的扰动矩阵 Q i j = F i ⊴ e T F j ⊴ e Q_{ij}=\mathcal{F}{i \unlhd e}^T\mathcal{F}{j \unlhd e} Qij=Fi⊴eTFj⊴e 即可得到 L F ‾ \overline{\mathcal{L}_{\mathcal{F}}} LF
Theorem 4.1
记 P = L F ‾ − L b l o c k P=\overline{\mathcal{L}{\mathcal{F}}} - \mathcal{L}{block} P=LF−Lblock 为 L b l o c k \mathcal{L}{block} Lblock对应的 perturbation matrix, ϕ = min i , j ; i ≠ j ∣ λ i − λ j ∣ , λ i \phi = \min{i,j;i\neq j}|\lambda_i - \lambda_j|,\lambda_i ϕ=mini,j;i=j∣λi−λj∣,λi 为 L b l o c k \mathcal{L}_{block} Lblock的特征值。则有,若 ∣ ∣ P ∣ ∣ 2 < ϕ 2 ||P||_2 < \frac{\phi}{2} ∣∣P∣∣2<2ϕ,则特征值的重复度会下降
也就是说,扰动只应当设的小一点,这里设为 F i ⊴ ( i , j ) = I − 2 u i j u i j T ∣ ∣ u i j ∣ ∣ 2 \mathcal{F}{i\unlhd (i,j)} = I-2\frac{u{ij}u_{ij}^T}{||u_{ij}||^2} Fi⊴(i,j)=I−2∣∣uij∣∣2uijuijT------Householder变换, u i j u_{ij} uij范围为 [ η / 10 , η ] , η [\eta/10, \eta], \eta [η/10,η],η 为足够小的值
4.3 PSL-GNN: Perturbed Sheaf Laplacian-Based GNN
理论上来讲,本方法可以与任意谱域GNN结合,这里以 GCN和 GPRGNN为例
4.3.1 PSL-GCN
即将 g ( Δ ) = I − Δ g(\Delta) = I-\Delta g(Δ)=I−Δ 改为 g ( Δ F ) = I − Δ F g(\Delta_{\mathcal{F}}) = I-\Delta_{\mathcal{F}} g(ΔF)=I−ΔF
最后一层处理完后添加 reshape 模块:
4.3.2 PSL-GPR
GPRGNN: Z = ∑ k = 0 K α k ( I − L ) k X 0 Z=\sum_{k=0}^K \alpha_k(I-\mathcal{L})^kX_0 Z=∑k=0Kαk(I−L)kX0
PSL-GPR: Y = ∑ k = 0 K α k ( I − L F ‾ ) k X Y=\sum_{k=0}^K \alpha_k(I-\overline{\mathcal{L}_{\mathcal{F}}})^kX Y=∑k=0Kαk(I−LF)kX
同样经过 reshape 和映射得到最终结果:
5. Theoretical Analysis
5.1 Expressiveness of PSL-GNN
Proposition 5.1
L b l o c k = L ⊗ I ∈ R n d × n d \mathcal{L}_{block} = \mathcal{L}\otimes I \in \mathbb{R}^{nd\times nd} Lblock=L⊗I∈Rnd×nd 的不同特征值数量和 L \mathcal{L} L相同,对应的GNN的能力也相同
Corollary 5.2-5.4
PSL-GNN 有更强的一维预测能力/丢失的频率信息更少/处理 frequency components 的能力更强
5.2 Perturbation Bounds of Eigenvalues
 perturbation 越小,特征值的变化也就越小,对于原图的结构信息的保持越好
perturbation 越小,特征值的变化也就越小,对于原图的结构信息的保持越好
6. Experiment
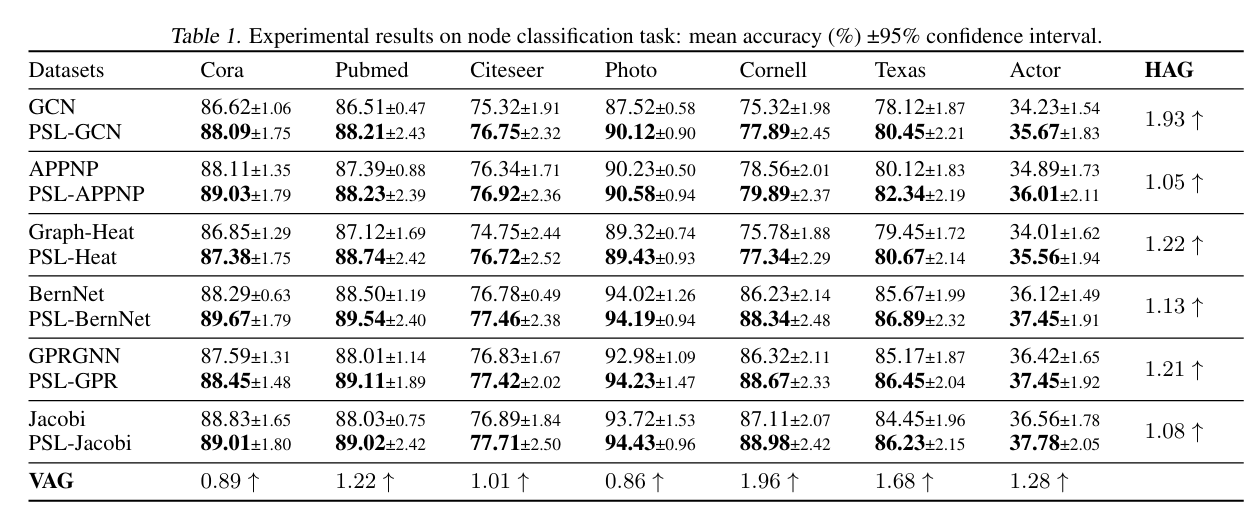
6.1 Evaluation on Real-World Datasets
1, Metrics:
-
VAG(Vertical Average Gain)

-
HAG(Horizontal Average Gain)
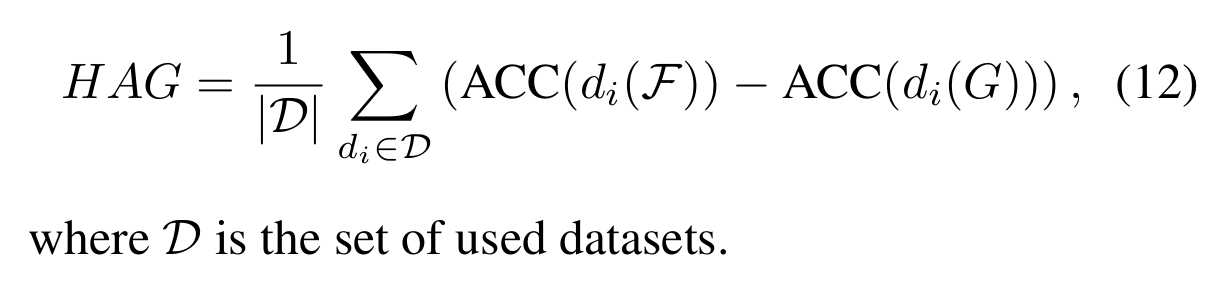
6.2 Ablation Study
Perturbed Sheaf Laplacian Matrix vs. General Sheaf Laplacian Matrix(GSL:不做任何限制地在整个正交空间里生成) vs. Normalized Graph Laplacian Matrix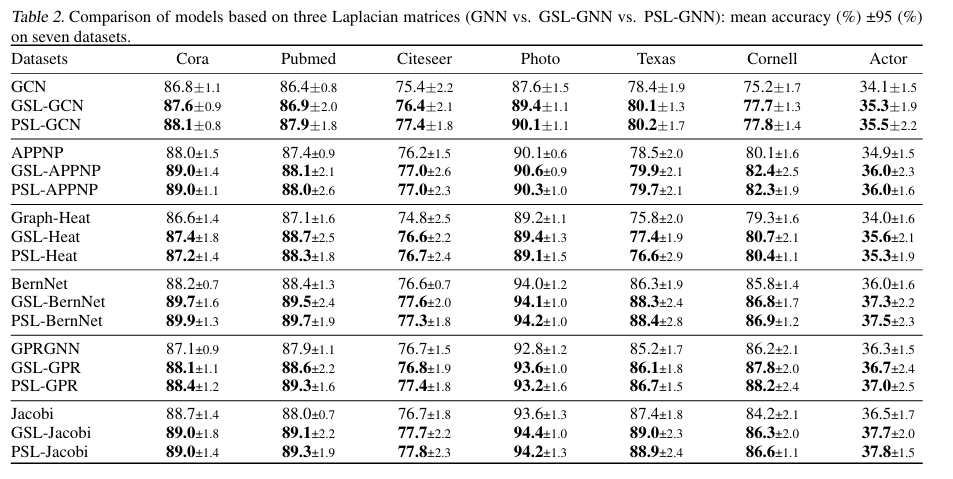
PSL-GNN 和 GSL-GNN的表现相当,说明二者学习到的结构趋于一致
6.3 The Number of Distinct Eigenvalues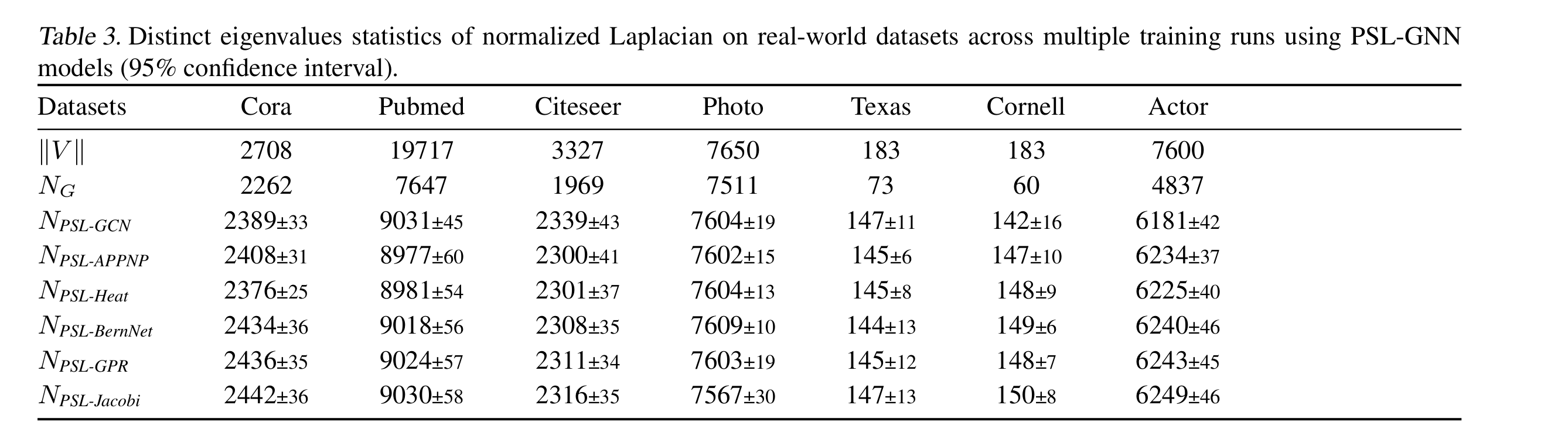
Pubmed 使用PSL之后的特征值数目仍然很少啊,但是效果竟然还可以