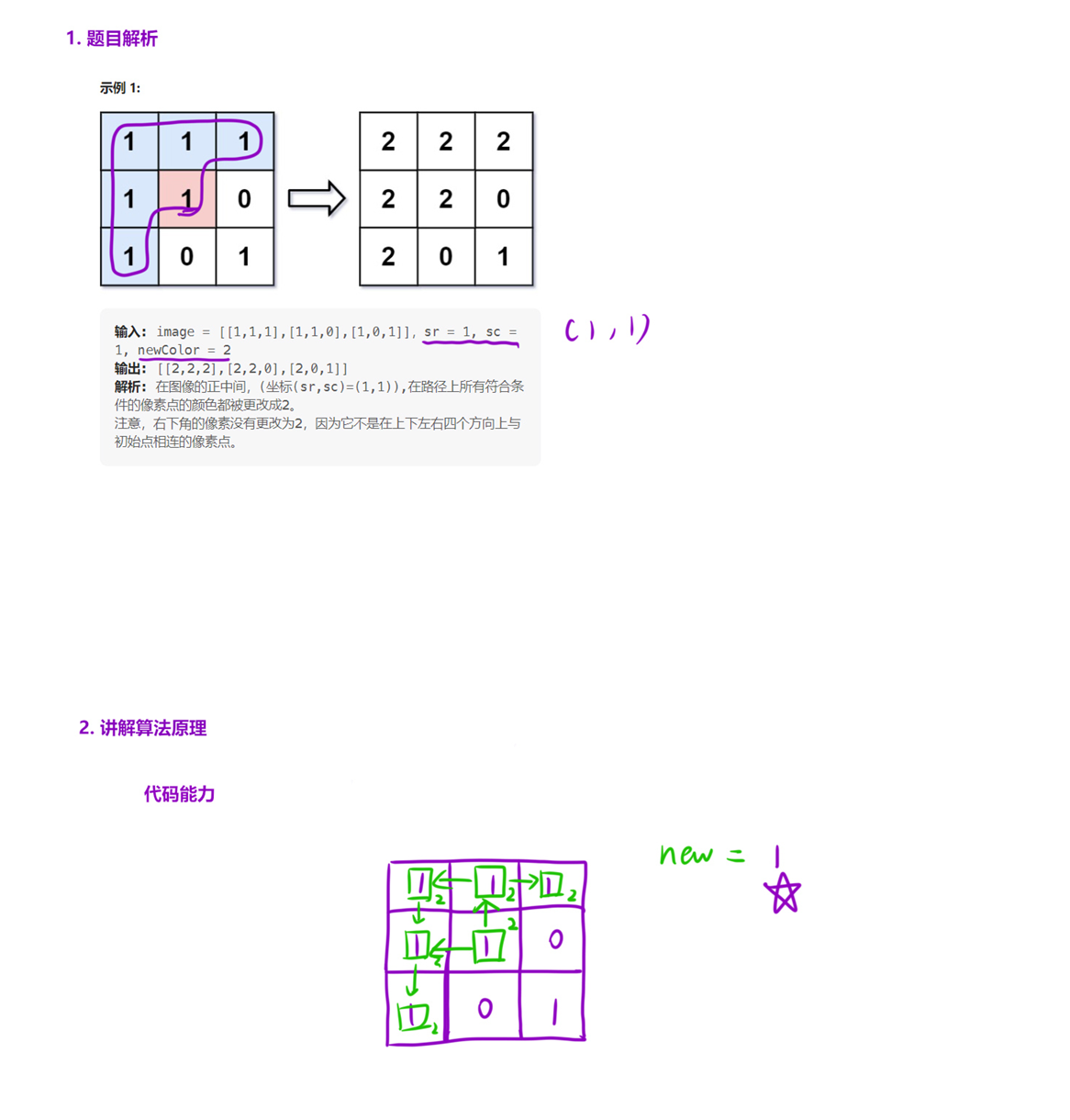
Flood Fill
一、先明确:Flood Fill 算法是什么?
Flood Fill(洪水填充算法)是一种区域填充算法 ,核心功能是:从指定的 "起始点" 出发,将与起始点 "连通且满足相同条件"(如颜色、数值相同)的所有像素 / 单元格,替换为目标值(如新颜色、新标记)。而 "DFS 实现" 是其最经典的方式之一 ------ 利用深度优先搜索(Depth-First Search,递归或栈模拟) 的 "先深后广" 特性,优先探索当前点的某一方向(如上下左右),直到走到 "边界" 或 "不满足条件的点",再回溯探索其他方向,最终遍历所有连通区域。
二、Flood Fill(DFS)的核心原理:3 个关键逻辑
1. 前提条件
要实现算法,需明确 3 个核心要素:
起始点 (x, y):填充的 "起点"(如鼠标点击的像素位置、矩阵中指定单元格);
连通规则:判断 "两点是否连通" 的标准,常用两种:
- 4 连通:只允许上下左右 4 个方向相邻(如 "十字形" 连通);
- 8 连通:允许上下左右 + 斜向共 8 个方向相邻(如 "米字形" 连通,适用于更复杂的区域);
8 个方向(上下左右 + 四个对角线方向)的向量表示如下,只需在原有 4 方向基础上补充斜向偏移即可:
cpp
// 8个方向的x偏移(dx)和y偏移(dy)
int dx[8] = {1, -1, 0, 0, 1, 1, -1, -1}; // 依次对应:下、上、右、左、右下、右上、左下、左上
int dy[8] = {0, 0, 1, -1, 1, -1, 1, -1};(dx[0], dy[0]) = (1, 0)→ 向下(x+1,y 不变)(dx[1], dy[1]) = (-1, 0)→ 向上(x-1,y 不变)(dx[2], dy[2]) = (0, 1)→ 向右(x 不变,y+1)(dx[3], dy[3]) = (0, -1)→ 向左(x 不变,y-1)(dx[4], dy[4]) = (1, 1)→ 向右下(x+1,y+1)(dx[5], dy[5]) = (1, -1)→ 向左下(x+1,y-1)(dx[6], dy[6]) = (-1, 1)→ 向右上(x-1,y+1)(dx[7], dy[7]) = (-1, -1)→ 向左上(x-1,y-1)
遍历逻辑与 4 方向一致,通过循环遍历这 8 个偏移量即可覆盖所有相邻点:
cpp
for (int i = 0; i < 8; i++) {
int new_x = x + dx[i];
int new_y = y + dy[i];
// 对(new_x, new_y)执行边界检查、填充等操作
}匹配条件:判断 "是否需要填充" 的规则(如 "当前单元格颜色 == 起始点颜色""当前数值 == 目标数值")。
2. DFS 实现的核心逻辑:"递归探索 + 回溯"
DFS 的本质是 "一条路走到头,走不通再回头换路",对应到 Flood Fill 中,就是:从起始点出发,先 "标记并填充" 当前点,再递归探索当前点的某一方向邻居(如先向上走),直到邻居不满足 "连通 + 匹配条件"(比如出界、颜色不同),再回溯到上一个点,探索下一个方向(如向上走不通,再向下),直到所有连通点都被填充。
用一句话总结:"填当前点 → 递归填邻居 → 邻居填完回溯",本质是通过递归栈维护 "待探索的路径"。
三、Flood Fill(DFS)的具体步骤(以 4 连通、矩阵颜色填充为例)
假设场景:一个 m×n 的像素矩阵,每个单元格存颜色值,要求从 (startX, startY) 出发,将所有 "4 连通且颜色 = 起始颜色" 的单元格,改为目标颜色。
步骤拆解:
-
边界与合法性检查 :若当前点
(x, y)超出矩阵范围(x<0或x>=m或y<0或y>=n),或当前点颜色≠起始颜色(说明不是要填充的区域),或当前点已被填充(避免重复递归),则直接 "返回"(终止当前递归分支)。 -
填充当前点 :将当前点
(x, y)的颜色改为目标颜色(完成 "填充",同时标记为 "已处理",避免重复探索)。 -
DFS 递归探索 4 个方向 :分别对当前点的 "上、下、左、右"4 个邻居点,重复执行步骤 1-3(递归调用自身)。例:当前点
(x,y),递归探索(x-1,y)(上)、(x+1,y)(下)、(x,y-1)(左)、(x,y+1)(右)。 -
递归终止:所有连通的 "待填充点" 都被处理后,递归栈逐层返回,算法结束。
四、关键注意点:避免 "死循环" 与 "重复递归"
DFS 实现时最容易出现的问题是 "递归栈溢出" 或 "重复处理",核心解决方式:
- 填充即标记:一旦填充当前点(改为目标颜色),就等同于 "标记为已处理"------ 后续递归检查时,因 "当前颜色≠起始颜色",会直接返回,避免重复递归;
- 优先检查边界:每次递归先判断 "是否出界、是否需要填充",不满足则立即返回,减少无效递归;
- 非递归实现(栈模拟):若矩阵过大,递归可能触发栈溢出,可改用 "栈" 模拟 DFS 流程(将待探索的点压入栈,弹出时处理并压入邻居,逻辑与递归一致)。
五、适用场景
Flood Fill(DFS)是非常实用的基础算法,常见应用包括:
- 图像编辑:画图软件的 "油漆桶工具"(填充相同颜色区域);
- 游戏开发:扫雷(标记连通的空白区域)、迷宫求解(探索连通路径)、消除类游戏(判断同色方块是否连通);
- 矩阵处理:标记二维数组中连通的相同数值区域(如地图中标记同一地块)。
通过以上拆解,能清晰看到:Flood Fill 的核心是 "区域连通性判断",而 DFS 是实现这一过程的 "遍历工具"------ 通过 "深度优先" 的探索方式,高效覆盖所有连通区域,完成填充任务。
题目练习
733. 图像渲染 - 力扣(LeetCode)
算法思路
可以利用 「深搜」 或者 「宽搜」,遍历到与该点相连的所有「像素相同的点」,然后将其修改成指定的像素即可。
递归函数设计
参数:
a. 原始矩阵;
b. 当前所在的位置;
c. 需要修改成的颜色。
函数体:
a. 先将该位置的颜色改成指定颜色(因为我们的判断,保证每次进入递归的位置都是需要修改的位置);
b. 遍历四个方向上的位置:
- 如果当前位置合法,并且与初试颜色相同,就递归进去。
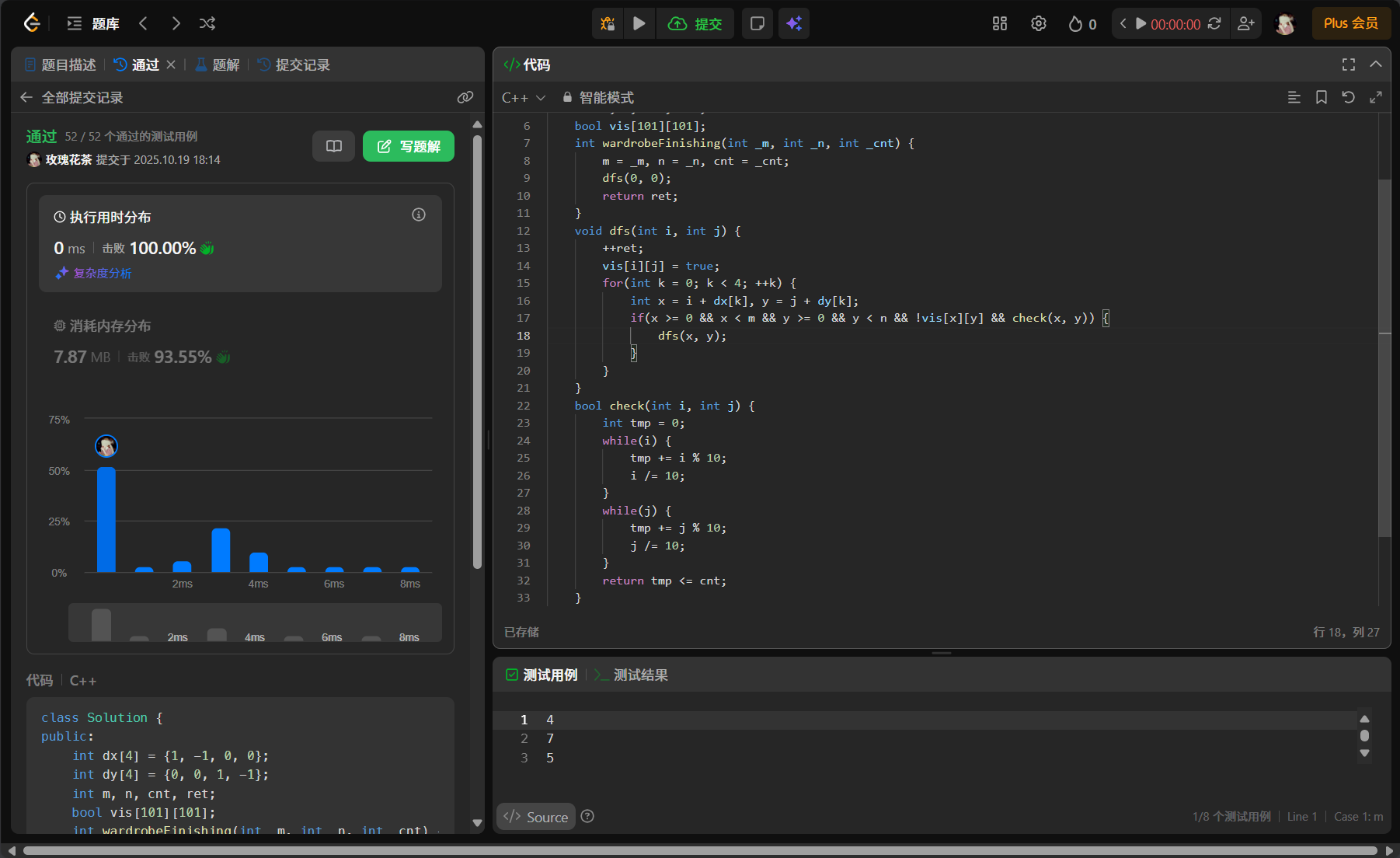
cpp
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
int color, m, n, dist;
vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int _color) {
if(image[sr][sc] == _color) return image;
dist = image[sr][sc], color = _color, m = image.size(), n = image[0].size();
dfs(image, sr, sc);
return image;
}
void dfs(vector<vector<int>>& image, int i, int j) {
image[i][j] = color;
for(int k = 0; k < 4; ++k) {
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == dist) {
dfs(image, x, y);
}
}
}
};
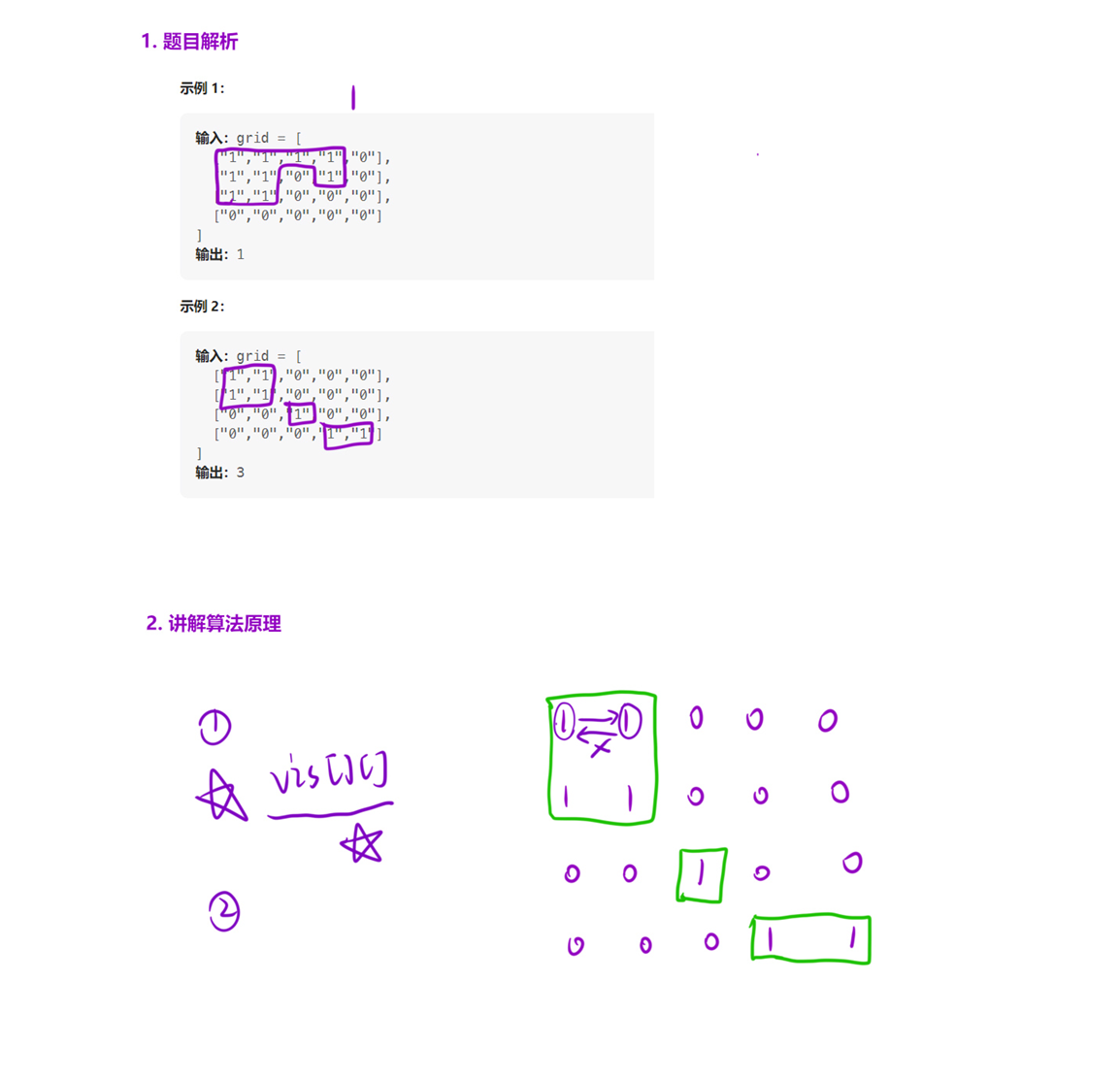
200. 岛屿数量 - 力扣(LeetCode)
算法思路
遍历整个矩阵,每次找到 「一块陆地」 的时候:
-
说明找到 「一个岛屿」 ,记录到最终结果
ret里面; -
并且将这个陆地相连的所有陆地,也就是这块 「岛屿」 ,全部 「变成海洋」 。这样的话,我们下次遍历到这块岛屿的时候,它 「已经是海洋」 了,不会影响最终结果。
-
其中 「变成海洋」 的操作,可以利用 「深搜」 和 「宽搜」 解决,其实就是 733. 图像渲染 这道题~
这样,当我们遍历完全部的矩阵的时候,ret 存的就是最终结果。
解法(dfs)
算法流程
-
初始化
ret = 0,记录目前找到的岛屿数量; -
双重循环遍历二维网格,每当遇到一块陆地,标记这是一个新的岛屿,然后将这块陆地相连的陆地全部变成海洋。
递归函数的设计
把当前格子标记为水;
向上、下、左、右四格递归寻找陆地,只有在下标位置合理的情况下,才会进入递归:
a. 下一个位置的坐标合理;
b. 并且下一个位置是陆地。
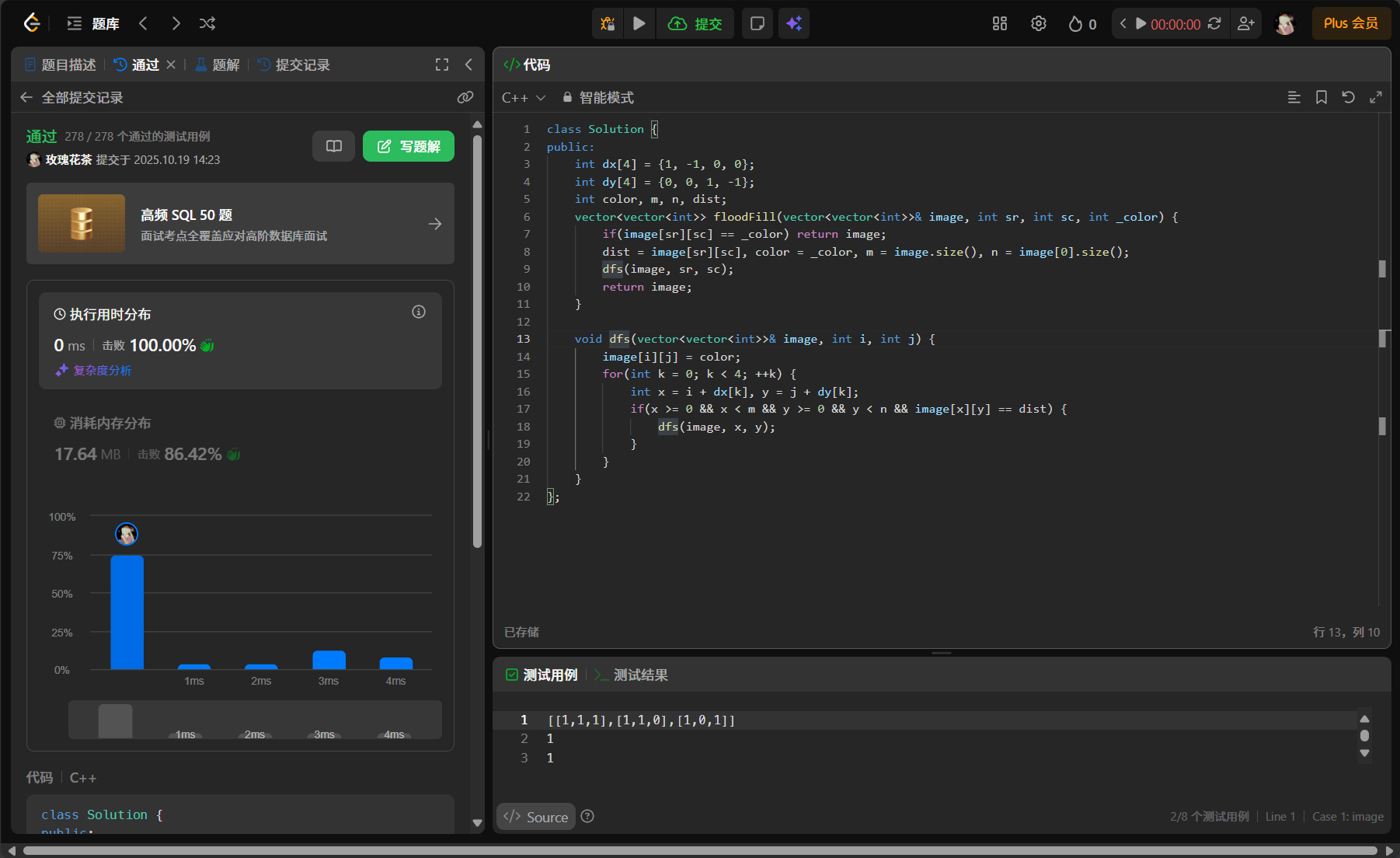
cpp
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0 ,0 ,1, -1};
bool vis[301][301];
int ret, m, n;
int numIslands(vector<vector<char>>& grid) {
m = grid.size(), n = grid[0].size();
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(grid[i][j] == '1' && !vis[i][j]) {
++ret;
dfs(grid, i, j);
}
return ret;
}
void dfs(vector<vector<char>>& grid, int i, int j) {
vis[i][j] = true;
for(int k = 0; k < 4; ++k) {
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] == '1') {
dfs(grid, x, y);
}
}
}
};
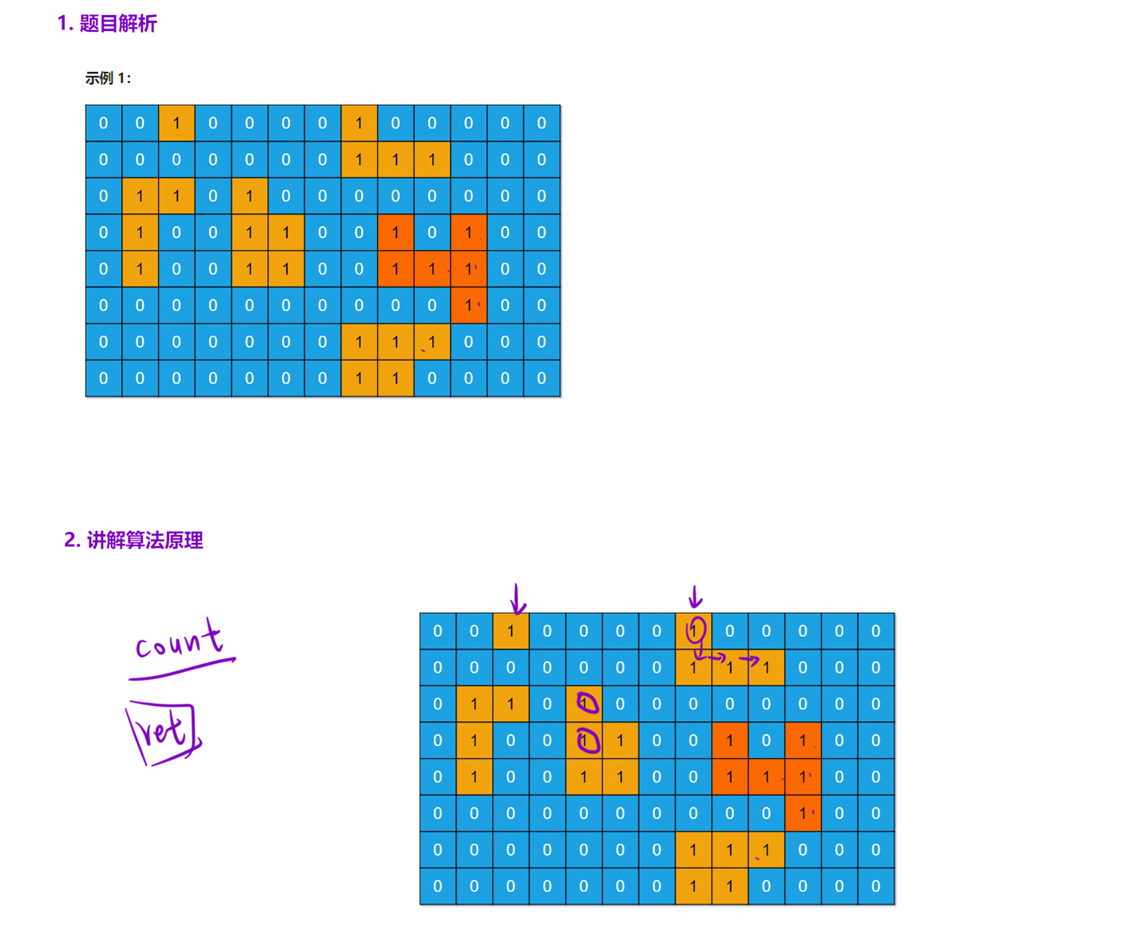
695. 岛屿的最大面积 - 力扣(LeetCode)
算法思路
遍历整个矩阵,每当遇到一块土地的时候,就用 「深搜」 或者 「宽搜」 将与这块土地相连的 「整个岛屿」 的面积计算出来。
然后在搜索得到的 「所有的岛屿面积」 求一个 「最大值」 即可。
在搜索过程中,为了 「防止搜到重复的土地」:
-
可以开一个同等规模的 「布尔数组」,标记一下这个位置是否已经被访问过;
-
也可以将原始矩阵的
1修改成0,但是这样操作会修改原始矩阵。
解法(深搜 dfs)
算法流程
主函数内:
a. 遍历整个数组,发现一块没有遍历到的土地之后,就用 dfs,将与这块土地相连的岛屿的面积求出来;
b. 然后将面积更新到最终结果 ret 中。
深搜函数 dfs 中:
a. 能够进到 dfs 函数中,说明是一个没遍历到的位置;
b. 标记一下已经遍历过,设置一个变量 S = 1(当前这个位置的面积为 1),记录最终的面积;
c. 上下左右遍历四个位置:
- 如果找到一块没有遍历到的土地,就将与这块土地相连的岛屿面积累加到
S上;
d. 循环结束后,S 中存的就是整块岛屿的面积,返回即可。
cpp
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
bool vis[51][51];
int m, n;
int maxAreaOfIsland(vector<vector<int>>& grid) {
m = grid.size(), n = grid[0].size();
int ret = 0;
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j) {
if(grid[i][j] == 1 && !vis[i][j]) ret = max(ret, dfs(grid, i, j));
}
return ret;
}
int dfs(vector<vector<int>>& grid, int i, int j) {
vis[i][j] = true;
int count = 1;
for(int k = 0; k < 4; ++k) {
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] == 1) {
count += dfs(grid, x, y);
}
}
return count;
}
};
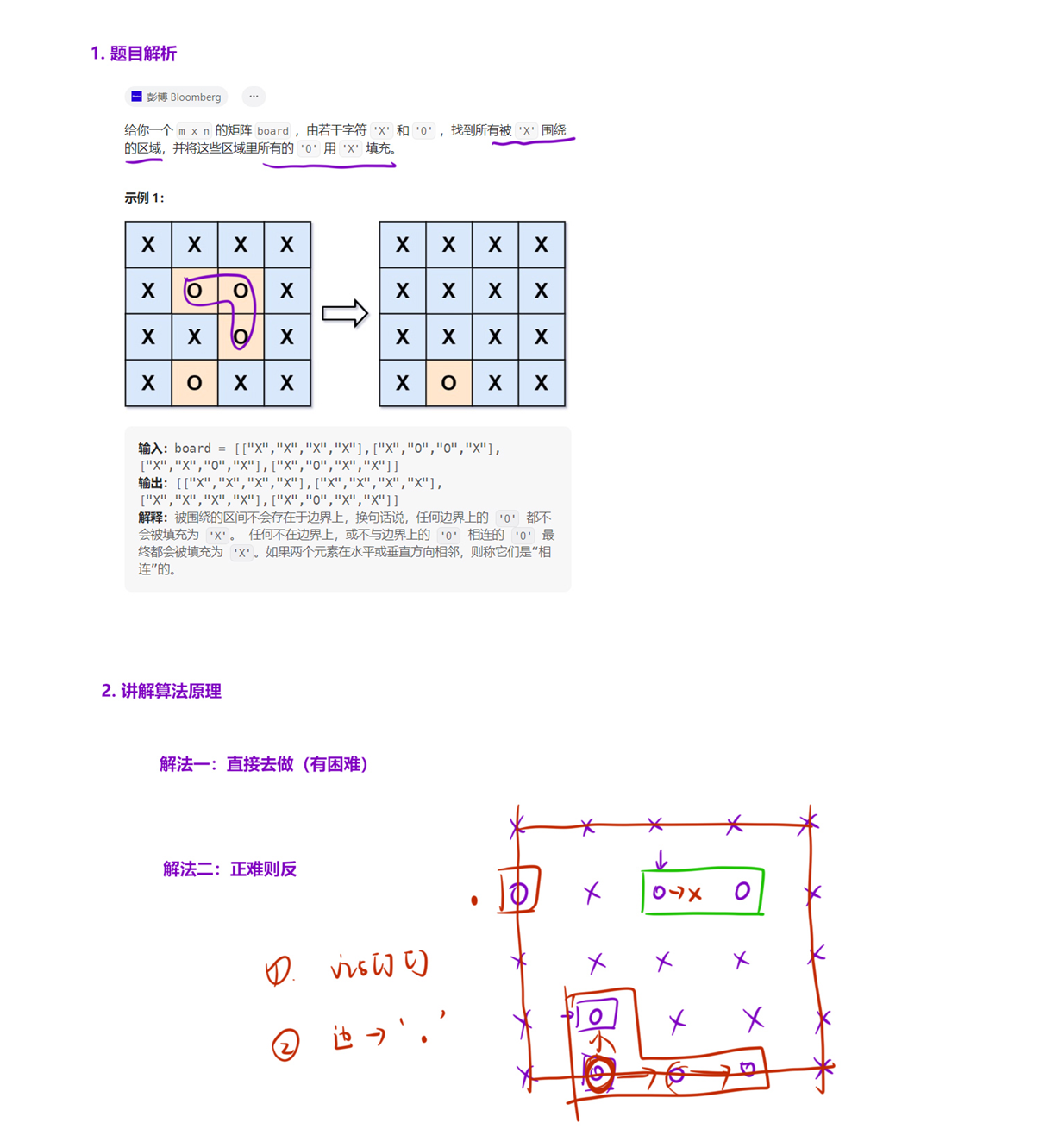
130. 被围绕的区域 - 力扣(LeetCode)
解法
算法思路
正难则反。
可以先利用 dfs 将与边缘相连的 '0' 区域做上标记,然后重新遍历矩阵,将没有标记过的 '0' 修改成 'X' 即可。
cpp
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
bool vis[201][201];
int m, n;
void solve(vector<vector<char>>& board) {
m = board.size(), n = board[0].size();
for(int i = 0; i < m; ++i) {
if(board[i][0] == 'O' && !vis[i][0]) dfs(board, i, 0);
if(board[i][n - 1] == 'O' && !vis[i][n - 1]) dfs(board, i, n - 1);
}
for(int j = 0; j < n; ++j) {
if(board[0][j] == 'O' && !vis[0][j]) dfs(board, 0, j);
if(board[m - 1][j] == 'O' && !vis[m - 1][j]) dfs(board, m - 1, j);
}
for(int i = 1; i < m - 1; ++i)
for(int j = 1; j < n - 1; ++j)
if(!vis[i][j] && board[i][j] == 'O') board[i][j] = 'X';
}
void dfs(vector<vector<char>>& board, int i, int j) {
vis[i][j] = true;
for(int k = 0; k < 4; ++k) {
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && board[x][y] == 'O') {
dfs(board, x, y);
}
}
}
};
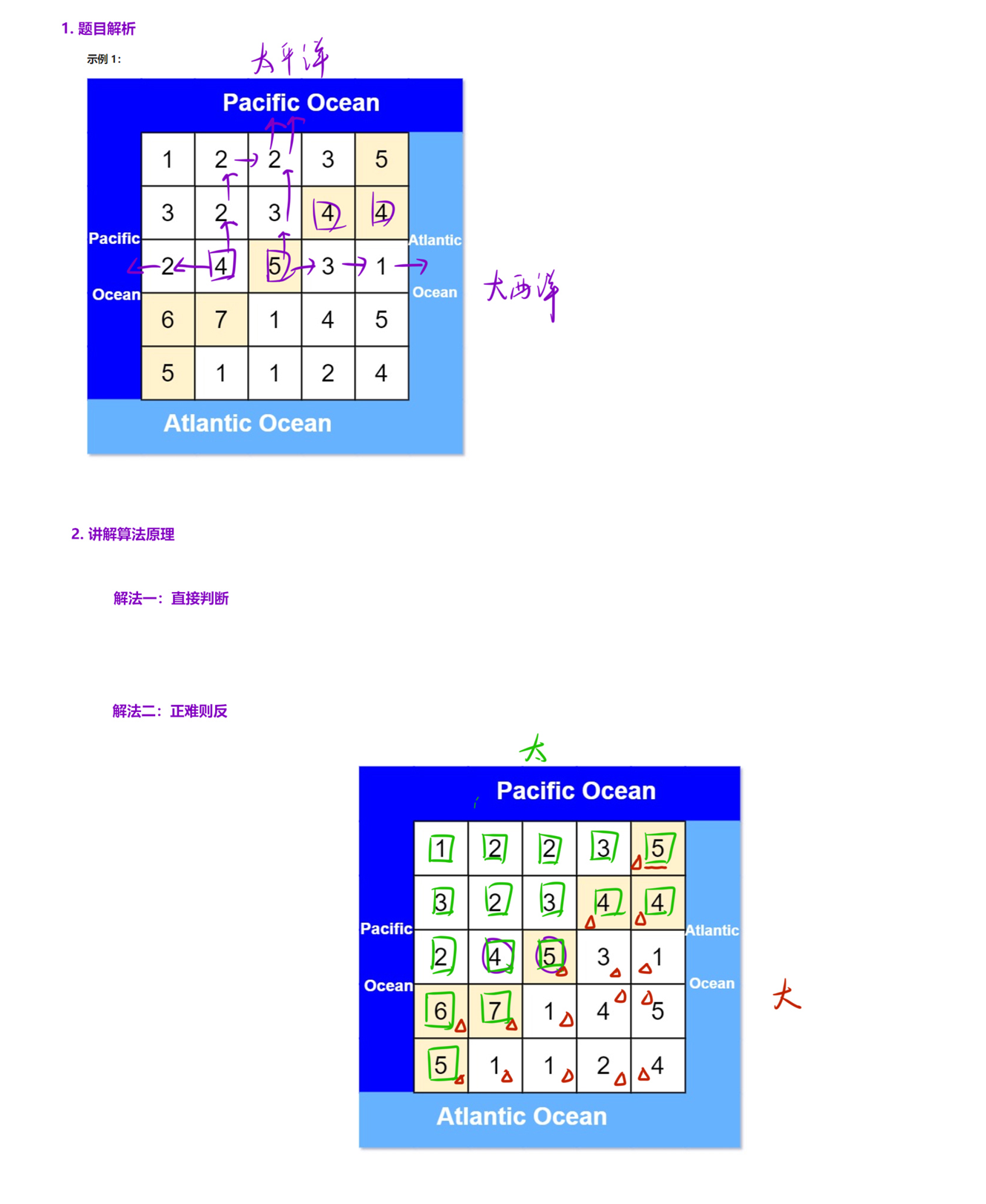
417. 太平洋大西洋水流问题 - 力扣(LeetCode)
解法
算法思路
正难则反。
如果直接去判断某一个位置是否既能到大西洋也能到太平洋,会重复遍历很多路径。
我们反着来,从大西洋沿岸开始反向 dfs ,这样就能找出那些点可以流向大西洋;同理,从太平洋沿岸也反向 dfs,这样就能找出那些点可以流向太平洋。那么,被标记两次的点,就是我们要找的结果。
cpp
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
int m, n;
vector<vector<int>> pacificAtlantic(vector<vector<int>>& heights) {
m = heights.size(), n = heights[0].size();
vector<vector<int>> pac(m, vector<int>(n));
auto atl = pac;
for(int i = 0; i < m; ++i) {
if(!pac[i][0]) dfs(heights, i, 0, pac);
if(!atl[i][n - 1])dfs(heights, i, n - 1, atl);
}
for(int j = 0; j < n; ++j) {
if(!pac[0][j]) dfs(heights, 0, j, pac);
if(!atl[m - 1][j])dfs(heights, m - 1, j, atl);
}
vector<vector<int>> ret;
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j)
if(pac[i][j] && atl[i][j]) ret.push_back({i, j});
return ret;
}
void dfs(vector<vector<int>>& heights, int i, int j, vector<vector<int>>& path) {
path[i][j] = true;
for(int k = 0; k < 4; ++k) {
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !path[x][y] && heights[x][y] >= heights[i][j]) {
dfs(heights, x, y, path);
}
}
}
};
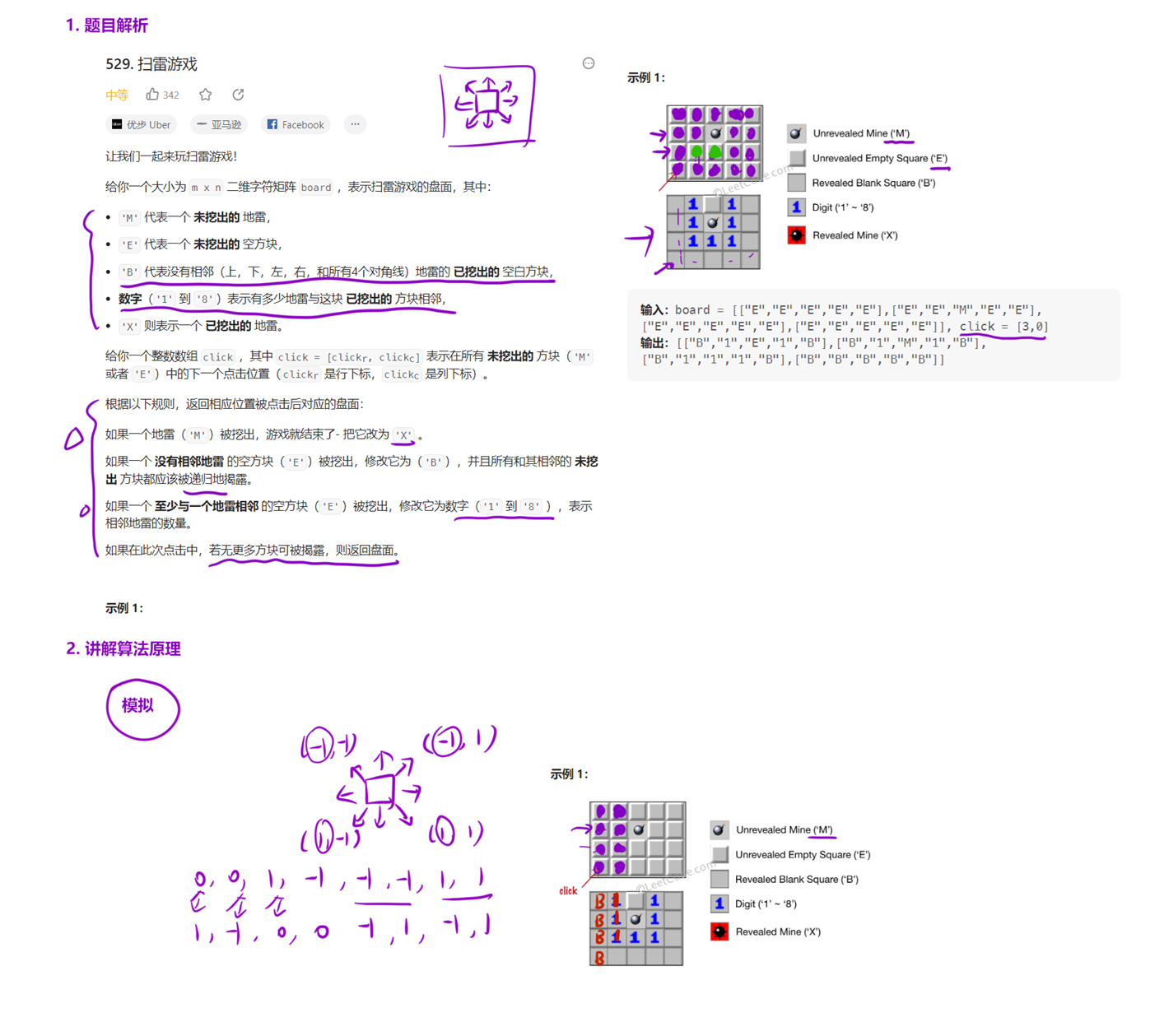
529. 扫雷游戏 - 力扣(LeetCode)
解法
算法思路
模拟类型的 dfs 题目。
首先要搞懂题目要求,也就是游戏规则。
从题目所给的点击位置开始,根据游戏规则,来一次 dfs 即可。
cpp
class Solution {
public:
int dx[8] = {1, -1, 0, 0, 1, 1, -1, -1};
int dy[8] = {0, 0, 1, -1, 1, -1, 1, -1};
int m, n;
vector<vector<char>> updateBoard(vector<vector<char>>& board, vector<int>& click) {
m = board.size(), n = board[0].size();
int x = click[0], y = click[1];
if(board[x][y] == 'M') {
board[x][y] = 'X';
return board;
}
dfs(board, x, y);
return board;
}
void dfs(vector<vector<char>>& board, int i, int j) {
int count = 0;
for(int k = 0; k < 8; ++k) {
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'M') ++count;
}
if(count) {
board[i][j] = count + '0';
return;
}
else {
board[i][j] = 'B';
for(int k = 0; k < 8; ++k) {
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'E') dfs(board, x, y);
}
}
}
};
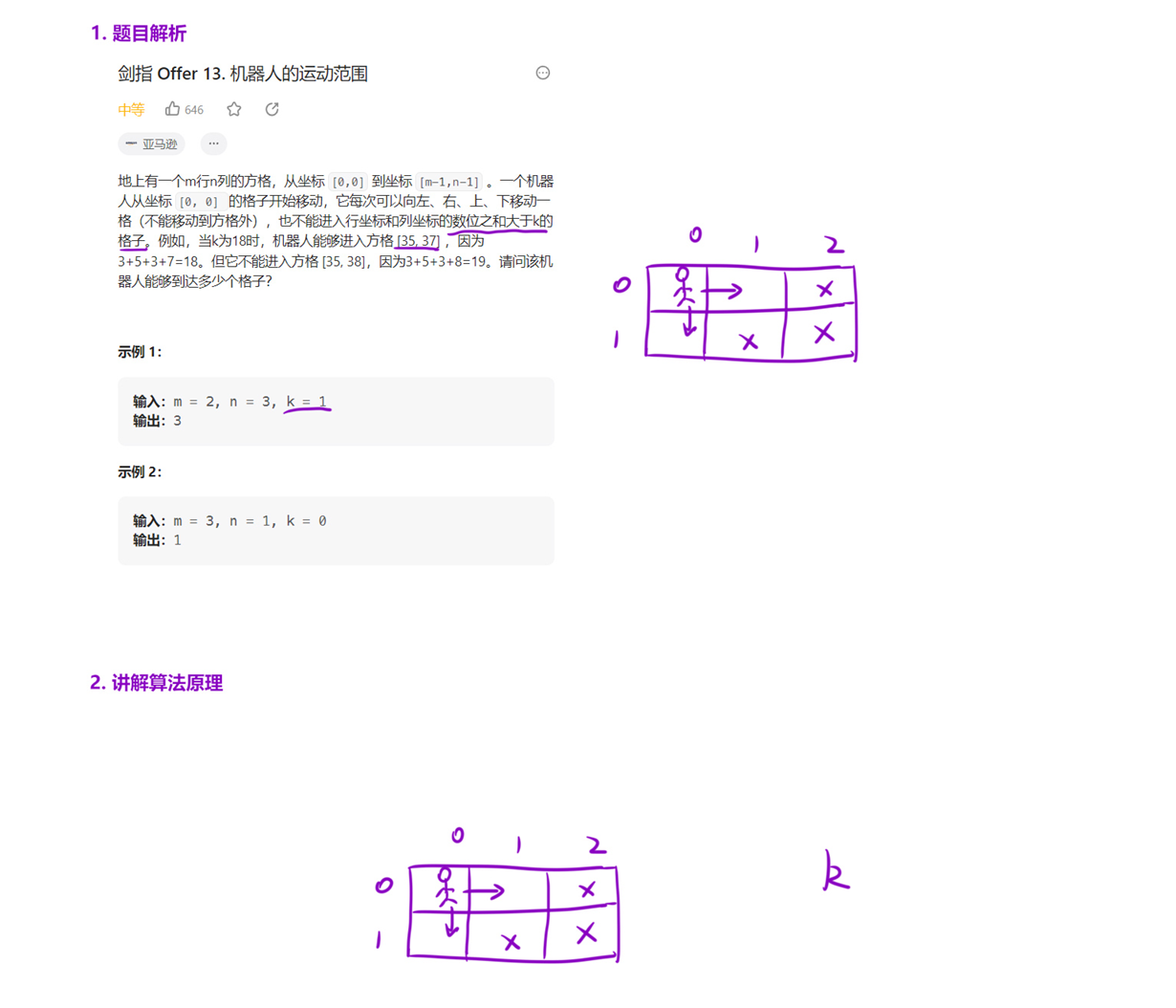
LCR 130. 衣橱整理 - 力扣(LeetCode)
算法思路
这是一道非常典型的 「搜索」 类问题。
我们可以通过 「深搜」 或者 「宽搜」 ,从 [0, 0] 点出发,按照题目的 「规则」 一直往 [m - 1, n - 1] 位置走。
同时,设置一个全局变量。每次走到一个合法位置,就将全局变量加一。当我们把所有能走到的路都走完之后,全局变量里面存的就是最终答案。
解法(dfs)
算法流程
递归函数设计:
a. 参数:当前所在的位置 [i, j],行走的边界 [m, n],坐标数位之和的边界 k;
b. 递归出口:
- i.
[i, j]的坐标不合法,也就是已经超出能走的范围; - ii.
[i, j]位置已经走过了(因此我们需要创建一个全局变量bool st[101][101],来标记当前位置是否走过); - iii.
[i, j]坐标的数位之和大于k;上述情况的任何一种都是递归出口。
c. 函数体内部:
- i. 如果这个坐标是合法的,就将全局变量
ret++; - ii. 然后标记一下
[i, j]位置已经遍历过; - iii. 然后去
[i, j]位置的上下左右四个方向去看看。
辅助函数:
a. 检测坐标 [i, j] 是否合法;
b. 计算出 i, j 的数位之和,然后与 k 作比较即可。
主函数 :调用递归函数,从 [0, 0] 点出发。
辅助的全局变量:
a. 二维数组 bool st[101][101]:标记 [i, j] 位置是否已经遍历过;
b. 变量 ret:记录一共到达多少个合法的位置。
c. 上下左右的四个坐标变换。
cpp
class Solution {
public:
int dx[4] = {1, -1, 0, 0};
int dy[4] = {0, 0, 1, -1};
int m, n, cnt, ret;
bool vis[101][101];
int wardrobeFinishing(int _m, int _n, int _cnt) {
m = _m, n = _n, cnt = _cnt;
dfs(0, 0);
return ret;
}
void dfs(int i, int j) {
++ret;
vis[i][j] = true;
for(int k = 0; k < 4; ++k) {
int x = i + dx[k], y = j + dy[k];
if(x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && check(x, y)) {
dfs(x, y);
}
}
}
bool check(int i, int j) {
int tmp = 0;
while(i) {
tmp += i % 10;
i /= 10;
}
while(j) {
tmp += j % 10;
j /= 10;
}
return tmp <= cnt;
}
};