hot 100 （1）—— 两数之和（哈希）

一、常规暴力解法（两层for循环）

java 复制代码

class Solution {
    public int[] twoSum(int[] nums, int target) {
        for(int i=0;i<nums.length;i++){
            for(int j=i+1;j<nums.length;j++){
                if(nums[i] + nums[j] == target){
                    return new int[]{i,j};
                }
            }
        }
        return new int[]{};
    }
}

代码功能解释

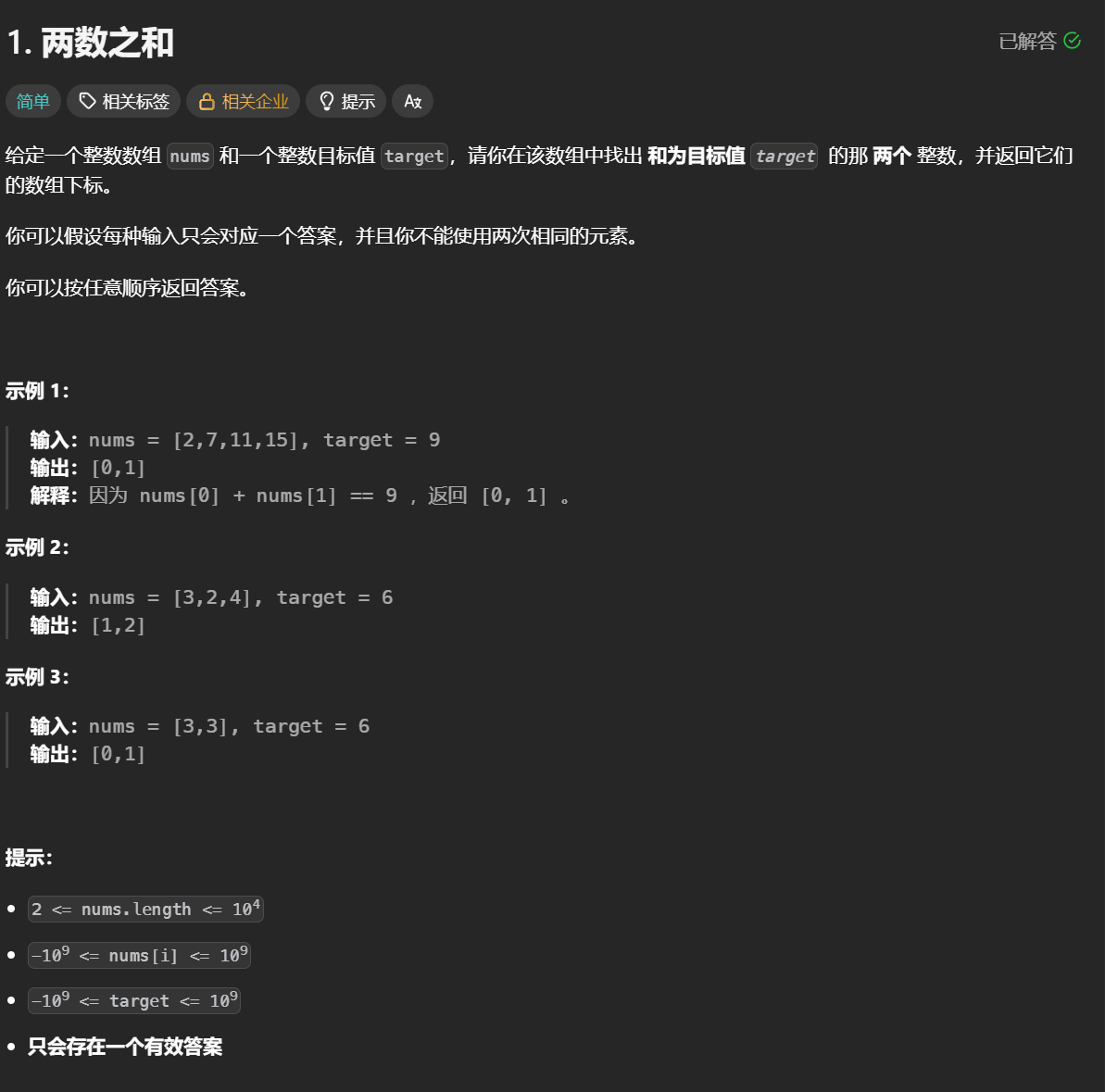
这段Java代码实现了两数之和问题的解法：给定一个整数数组nums和一个目标值target，找到数组中两个数相加等于target的索引，并返回这两个索引（题目默认有且只有一个有效答案）。

核心逻辑是通过两层循环遍历数组：

• 外层循环（i）从数组第一个元素开始，依次取每个元素作为"基准元素"；

• 内层循环（j）从i+1开始，遍历"基准元素"之后的所有元素，检查两者之和是否等于target；

• 若满足条件，直接返回包含i和j的数组；若遍历结束未找到，返回空数组（实际题目场景下不会触发）。

时间复杂度

• 复杂度级别：O(n²)（n为数组nums的长度）。

• 原因：外层循环执行n次，内层循环针对每个i分别执行n-1、n-2...1次，整体执行次数约为n(n-1)/2，属于平方级别的时间开销，数据量增大时效率会显著下降。

空间复杂度

• 复杂度级别：O(1)（常数级）。

• 原因：算法仅使用了i、j两个循环变量，未额外创建与数组长度n相关的存储结构（如数组、哈希表等），占用的内存空间不随输入数据量变化。

二、最优解法（HashMap）

java 复制代码

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i=0;i<nums.length;i++){
            if(map.containsKey(target - nums[i])){
                return new int[]{map.get(target - nums[i]),i};
            }
            map.put(nums[i],i);
        }
        return new int[]{};
    }
}

代码功能解释

这段Java代码是两数之和的优化解法，核心思路是用哈希表（HashMap）存储已遍历元素，实现"一次遍历找答案"，步骤如下：

◦ 初始化HashMap，键存数组元素值，值存该元素的原始索引；

◦ 遍历数组（索引i从0开始）：

计算"目标补数"：target - nums $i$ （即与当前元素相加等于target的数）；
检查哈希表中是否存在该"补数"：若存在，直接返回 $补数的索引, 当前索引i$ （补数先存入，索引更小）；
若不存在，将当前元素nums $i$ 和其索引i存入哈希表，继续遍历；

◦ 题目默认有唯一解，遍历结束前必返回结果，末尾空数组仅为语法补充。

时间复杂度

• 复杂度级别：O(n)（n为数组nums的长度）。

• 原因：仅需遍历数组一次，哈希表的containsKey和put操作均为O(1) 平均时间复杂度，整体无嵌套循环，时间开销随数组长度线性增长。

空间复杂度

• 复杂度级别：O(n)（线性级）。

• 原因：最坏情况下（如答案在数组末尾），需将数组中n-1个元素存入哈希表，哈希表占用空间随数组长度线性增长，故为O(n)。

三、额外解法（二维数组dp + 双指针）

java 复制代码

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int n = nums.length;
        int[][] dp = new int[n][2];
        for(int i=0;i<n;i++){
            dp[i][0] = nums[i];
            dp[i][1] = i;
        }
        Arrays.sort(dp, (a,b) -> a[0] - b[0]);//一定要排序！！！,并且要先填充dp再排序！！！
        int left = 0;
        int right = nums.length - 1;
        while(left < right){
            int sum = dp[left][0] + dp[right][0];
            if(sum == target){
                return new int[]{dp[left][1],dp[right][1]};
            }else if(sum < target){
                left++;
            }else{
                right--;
            }
        }
        return new int[]{};
    }
}

代码功能解释

这段Java代码同样解决两数之和问题，核心思路是"先排序，再双指针"，步骤如下：

保存原始索引：创建二维数组dp（每行存 $数组元素值, 元素原始索引$ ），避免排序后丢失原始索引（题目要求返回原始索引）；
排序数组：按dp每行的第一个元素（即原数组的数值）升序排序，这是双指针查找的前提；
双指针查找：左指针left从数组开头出发，右指针right从数组末尾出发，计算两指针指向元素的和：

◦ 若和等于target，直接返回两元素的原始索引（dp $left$ $1$ 和dp $right$ $1$ ）；

◦ 若和小于target，左指针右移（增大数值）；

◦ 若和大于target，右指针左移（减小数值）；

若遍历结束未找到（题目默认有解，此情况不触发），返回空数组。
时间复杂度

• 复杂度级别：O(n log n)（n为数组nums的长度）。

• 原因：算法耗时主要在排序步骤（Arrays.sort采用双轴快排，时间复杂度为O(n log n)），后续双指针遍历仅需O(n)，整体由排序主导，故为O(n log n)。

空间复杂度

• 复杂度级别：O(n)（线性级）。

• 原因：额外创建了二维数组dp，其长度与原数组nums一致（n行2列），占用空间随n线性增长，故为O(n)。