基于MIMO FMCW雷达的二维角度分析多径抑制技术
J. Kim, J. Jung, S. Lim and S. -C. Kim, "Multipath Suppression Using 2-D Angle Analysis Based on the MIMO FMCW Radar," in IEEE Transactions on Instrumentation and Measurement, vol. 74, pp. 1-12, 2025, Art no. 8500212, doi: 10.1109/TIM.2024.3500061.
1. 引言与研究背景
室内人体检测是实现智能家居系统的关键前提。然而,雷达传感器在室内环境中会遭受严重的多径效应影响,多径信号产生的虚假目标极大地降低了雷达系统的稳定性。本研究深入分析了传统多输入多输出(MIMO)波束形成方法使用虚拟天线阵列时在多径抑制方面的局限性,并提出了一种基于MIMO FMCW雷达的路径匹配算法。该算法利用信号路径的角度特性来识别直接路径和一阶多径对,通过分别考虑离开角(AoD)和到达角(AoA)进行二维角度分析,同时解决了大天线间距引起的角度模糊问题。
2. FMCW雷达信号模型
2.1 基本信号模型
FMCW雷达发射的线性调频信号,其瞬时频率随时间线性增加。发射的调频信号表达式为:
s(t)=exp[j2π(f0t+St22)]rect(t−Tsw/2Tsw)(1)s(t) = \exp\left[j2\pi\left(f_0t + \frac{St^2}{2}\right)\right]\text{rect}\left(\frac{t - T_{sw}/2}{T_{sw}}\right) \tag{1}s(t)=exp[j2π(f0t+2St2)]rect(Tswt−Tsw/2)(1)
其中f0f_0f0是载波频率,S=B/TswS = B/T_{sw}S=B/Tsw是时频斜率,BBB是扫频带宽,TswT_{sw}Tsw是扫频持续时间,rect(⋅)\text{rect}(\cdot)rect(⋅)是矩形函数。发射信号经过目标反射后,雷达接收到的信号是发射信号s(t)s(t)s(t)的延迟和缩放回波的叠加:
r(t)=∑k=0K−1aks(t−2Rkc)(2)r(t) = \sum_{k=0}^{K-1} a_k s\left(t - \frac{2R_k}{c}\right) \tag{2}r(t)=k=0∑K−1aks(t−c2Rk)(2)
其中KKK是往返路径数,ccc是光速,aka_kak和RkR_kRk分别是第kkk条路径对应的复振幅和距离。
接收信号经过解调处理,即调频信号与接收信号共轭混合。所得到的差拍信号,在忽略关于1/c1/c1/c的二阶项后,可以近似为:
x(t)=r∗(t)s(t)≈∑k=0K−1ak∗exp[j2π(2SRktc+2Rkλ)]⋅rect(t−Tsw/2Tsw)(3)x(t) = r^*(t)s(t) \approx \sum_{k=0}^{K-1} a_k^* \exp\left[j2\pi\left(\frac{2SR_kt}{c} + \frac{2R_k}{\lambda}\right)\right] \cdot \text{rect}\left(\frac{t - T_{sw}/2}{T_{sw}}\right) \tag{3}x(t)=r∗(t)s(t)≈k=0∑K−1ak∗exp[j2π(c2SRkt+λ2Rk)]⋅rect(Tswt−Tsw/2)(3)
其中λ=c/f0\lambda = c/f_0λ=c/f0是对应于调频信号起始频率的波长。这里假设2Rk/c≪Tsw2R_k/c \ll T_{sw}2Rk/c≪Tsw以保证发射和接收信号的时间重叠。
2.2 MIMO雷达扩展模型
对于MIMO雷达系统,假设发射和接收天线阵列是均匀线性阵列,具有NtxN_{tx}Ntx个发射天线和NrxN_{rx}Nrx个接收天线,天线间距分别为dtxd_{tx}dtx和drxd_{rx}drx。多个发射天线采用时分复用方案工作。由于信号传播路径长度的差异,天线之间会根据传播角度产生相位偏移。第(ntx)(n_{tx})(ntx)个发射天线和第(nrx)(n_{rx})(nrx)个接收天线对的差拍信号可以表示为:
x(t,ntx,nrx)≈∑k=0K−1ak∗exp[j2π(2SRktc+2Rkλ+sinϕkdtxntxλ+sinψkdrxnrxλ)]⋅rect(t−Tsw/2Tsw)(4)x(t, n_{tx}, n_{rx}) \approx \sum_{k=0}^{K-1} a_k^* \exp\left[j2\pi\left(\frac{2SR_kt}{c} + \frac{2R_k}{\lambda} + \frac{\sin\phi_k d_{tx}n_{tx}}{\lambda} + \frac{\sin\psi_k d_{rx}n_{rx}}{\lambda}\right)\right] \cdot \text{rect}\left(\frac{t - T_{sw}/2}{T_{sw}}\right) \tag{4}x(t,ntx,nrx)≈k=0∑K−1ak∗exp[j2π(c2SRkt+λ2Rk+λsinϕkdtxntx+λsinψkdrxnrx)]⋅rect(Tswt−Tsw/2)(4)
其中ϕk\phi_kϕk和ψk\psi_kψk分别是第kkk条路径的AoD和AoA,从雷达视轴逆时针测量。
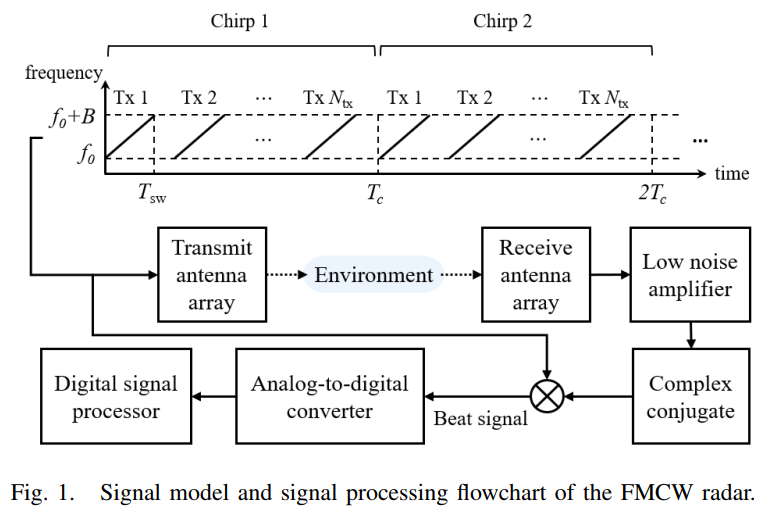
图1描述 :图1展示了FMCW雷达的信号模型和信号处理流程图。系统通过时分复用方式依次处理多个调频信号,以获得多个时刻的目标信号。差拍信号经ADC采样后输入数字信号处理器来估计目标信息。通过分析时域采样、发射天线和接收天线方向的频率分量,可以分别估计距离、AoD和AoA。包含MMM个连续调频的数据定义为一帧,它们被认为是相干的并同时处理。
3. 多径传播分析
3.1 多径信号的阶次分类
多径信号可以按阶次分类,阶次定义为额外反射的次数。通常,多径信号的功率随着阶次增加而降低,这是由于额外反射造成的功率损失。考虑到高阶多径的功率相对较低,本研究主要考虑一阶多径,忽略其他高阶多径。
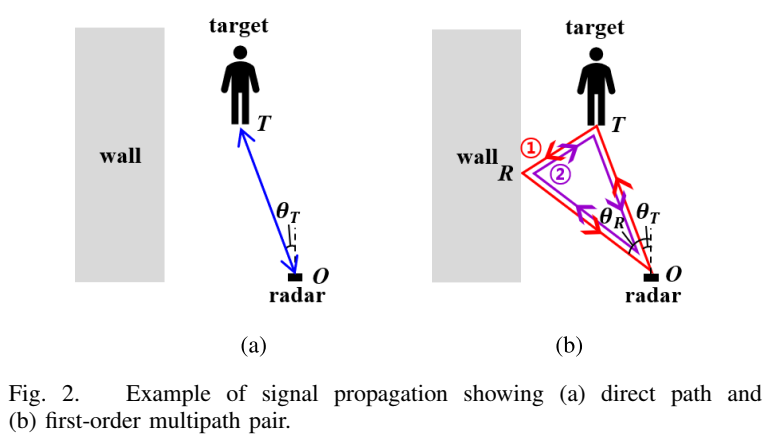
图2描述:图2展示了包含目标和墙壁的环境中的多径传播示例。图2(a)显示了直接路径,它只从目标反射一次,没有任何额外反射。由于直接路径包含准确的目标信息(如距离和角度),它被认为是期望路径。图2(b)显示了一阶多径,它们有来自墙壁的额外反射。这些多径可能产生包含不准确目标信息的虚假目标。
3.2 一阶多径的关键特性
研究发现一阶多径信号相对于直接路径信号具有两个独特的特性:
特性1:AoD和AoA不相同。一阶多径信号的AoD和AoA不相同,因为发射信号朝向第一个反射点发出,而从第二个反射点到达雷达。这种差异扭曲了角度信息,使传统角度估计方法难以应用。
特性2:多径对的存在 。由于互易性,一阶多径信号成对存在,称为多径对。每个多径对包含两个方向相反的多径信号,它们的AoD和AoA相互交换。例如在图2(b)中,红色路径的AoD为θT\theta_TθT、AoA为θR\theta_RθR,紫色路径的AoD为θR\theta_RθR、AoA为θT\theta_TθT。我们使用记号{θT,θR}\{\theta_T, \theta_R\}{θT,θR}或等价的{θR,θT}\{\theta_R, \theta_T\}{θR,θT}来表示多径对的角度。
直接路径和一阶多径对的距离可以分别表示为:
Rd=OT,Rm=OT+OR+TR2(5)R_d = OT, \quad R_m = \frac{OT + OR + TR}{2} \tag{5}Rd=OT,Rm=2OT+OR+TR(5)
其中OOO、TTT和RRR分别代表雷达、目标和额外反射点的位置,满足Rd<RmR_d < R_mRd<Rm。角度可以表示为:
θd=θT,θm={θT,θR}(6)\theta_d = \theta_T, \quad \theta_m = \{\theta_T, \theta_R\} \tag{6}θd=θT,θm={θT,θR}(6)
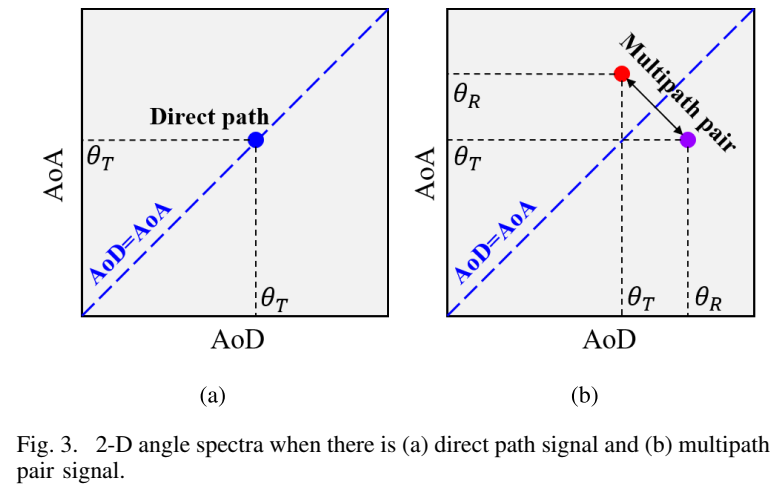
图3描述:图3展示了存在直接路径信号和多径对信号时的二维角度谱。图3(a)中,直接路径信号出现在代表相同AoD和AoA的对角线上。图3(b)中,多径对关于对角线对称出现,因为多径对中包含的两个信号具有交换的AoD和AoA。因此,通过分析二维角度谱中的角度特性,可以识别直接路径和多径对。
4. 传统角度估计方法及其局限性
4.1 MVDR波束形成实现
MVDR方法通过调整指向期望方向的波束形成向量,同时自适应地抑制来自其他方向的干扰信号。获得指向角度θ\thetaθ的波束形成向量wθ\mathbf{w}_\thetawθ的优化问题为:
minwθwθHRwθ,s.t. wθHa(θ)=1(7)\min_{\mathbf{w}\theta} \mathbf{w}\theta^H \mathbf{R}\mathbf{w}\theta, \quad \text{s.t. } \mathbf{w}\theta^H \mathbf{a}(\theta) = 1 \tag{7}wθminwθHRwθ,s.t. wθHa(θ)=1(7)
其中R=E[xxH]\mathbf{R} = E[\mathbf{x}\mathbf{x}^H]R=E[xxH]是信号协方差矩阵,x∈CN×1\mathbf{x} \in \mathbb{C}^{N \times 1}x∈CN×1是天线阵列的采样信号向量,NNN是天线数,a(θ)=[1,exp(j2πdsinθ/λ),...,exp(j2π(N−1)dsinθ/λ)]T\mathbf{a}(\theta) = [1, \exp(j2\pi d\sin\theta/\lambda), \ldots, \exp(j2\pi(N-1)d\sin\theta/\lambda)]^Ta(θ)=[1,exp(j2πdsinθ/λ),...,exp(j2π(N−1)dsinθ/λ)]T是指向角度θ\thetaθ的阵列导向向量。
协方差矩阵R\mathbf{R}R通常使用空间平滑的集合平均来近似为样本协方差矩阵:
R≈12Nsp(XXH+JX∗XTJ)(8)\mathbf{R} \approx \frac{1}{2N_{sp}}\left(\mathbf{XX}^H + \mathbf{JX}^*\mathbf{X}^T\mathbf{J}\right) \tag{8}R≈2Nsp1(XXH+JX∗XTJ)(8)
最优波束形成向量wθ,opt\mathbf{w}_{\theta,opt}wθ,opt和相应的角度谱P(θ)P(\theta)P(θ)为:
wθ,opt=R−1a(θ)aH(θ)R−1a(θ)(9)\mathbf{w}_{\theta,opt} = \frac{\mathbf{R}^{-1}\mathbf{a}(\theta)}{\mathbf{a}^H(\theta)\mathbf{R}^{-1}\mathbf{a}(\theta)} \tag{9}wθ,opt=aH(θ)R−1a(θ)R−1a(θ)(9)
P(θ)=wθ,optHRwθ,opt=1aH(θ)R−1a(θ)(10)P(\theta) = \mathbf{w}{\theta,opt}^H\mathbf{R}\mathbf{w}{\theta,opt} = \frac{1}{\mathbf{a}^H(\theta)\mathbf{R}^{-1}\mathbf{a}(\theta)} \tag{10}P(θ)=wθ,optHRwθ,opt=aH(θ)R−1a(θ)1(10)
对于MIMO天线阵列,使用虚拟天线阵列的概念,Ntx×NrxN_{tx} \times N_{rx}Ntx×Nrx MIMO天线阵列转换为虚拟的1×NtxNrx1 \times N_{tx}N_{rx}1×NtxNrx单输入多输出天线阵列。虚拟天线阵列的导向向量表示为av(θ)=atx(θ)⊗arx(θ)\mathbf{a}v(\theta) = \mathbf{a}{tx}(\theta) \otimes \mathbf{a}_{rx}(\theta)av(θ)=atx(θ)⊗arx(θ),相应的角度谱为:
Pv(θ)=1avH(θ)R−1av(θ)(11)P_v(\theta) = \frac{1}{\mathbf{a}_v^H(\theta)\mathbf{R}^{-1}\mathbf{a}_v(\theta)} \tag{11}Pv(θ)=avH(θ)R−1av(θ)1(11)
4.2 多径抑制的失效案例分析
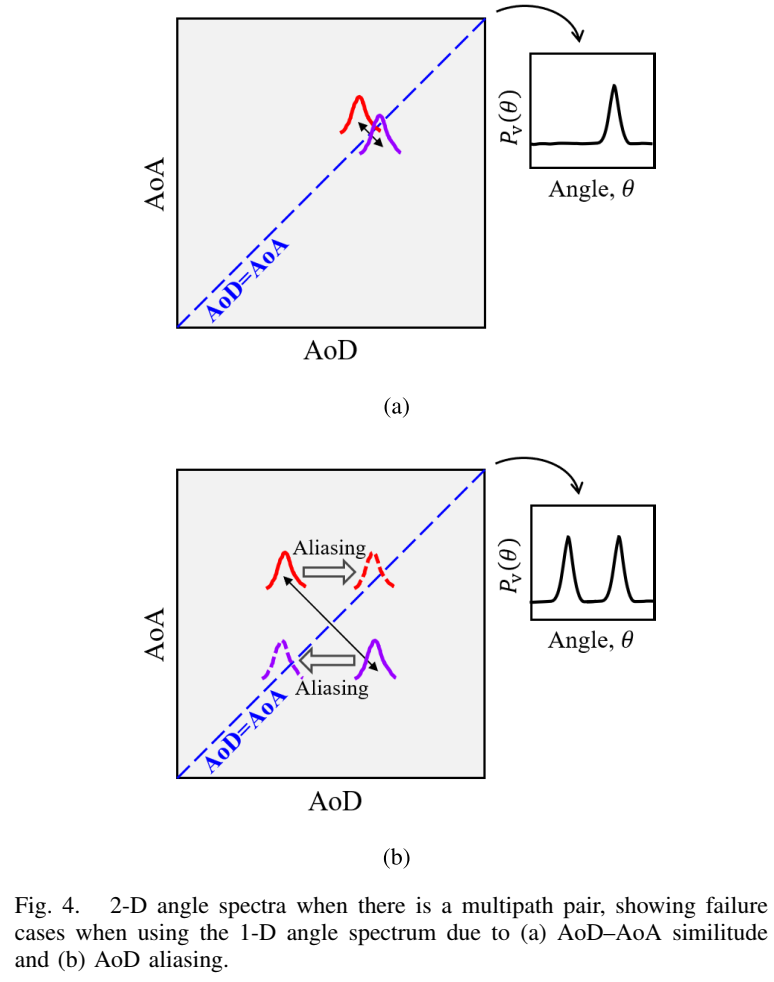
图4描述 :图4展示了使用一维角度谱时的两种不同失效案例。假设存在多径对{θ1,θ2}\{\theta_1, \theta_2\}{θ1,θ2}。图4(a)显示了当θ1\theta_1θ1和θ2\theta_2θ2之间的差异不够大时的AoD-AoA相似情况,多径信号无法被完全抑制。图4(b)显示了由于AoD混叠导致的失效情况,当θ1\theta_1θ1和θ2\theta_2θ2是彼此的模糊角度时,多径信号无法被抑制。
当天线间距为Gλ/2G\lambda/2Gλ/2(GGG为正整数)时,在−90°-90°−90°到90°90°90°之间存在GGG个无法区分的模糊角度:
θg=arcsin[mod(sinθ0+2gG+1,2)−1],g=1,...,G−1(12)\theta_g = \arcsin\left[\text{mod}\left(\sin\theta_0 + \frac{2g}{G} + 1, 2\right) - 1\right], \quad g = 1, \ldots, G-1 \tag{12}θg=arcsin[mod(sinθ0+G2g+1,2)−1],g=1,...,G−1(12)
当θ1\theta_1θ1和θ2\theta_2θ2是模糊的AoD时,发射天线阵列的导向向量变得相同,即atx(θ1)=atx(θ2)\mathbf{a}{tx}(\theta_1) = \mathbf{a}{tx}(\theta_2)atx(θ1)=atx(θ2)。此时多径对{θ1,θ2}\{\theta_1, \theta_2\}{θ1,θ2}的基向量变得与两个直接路径θ1\theta_1θ1和θ2\theta_2θ2的基向量之和相同:
atx(θ1)⊗arx(θ2)+atx(θ2)⊗arx(θ1)=atx(θ2)⊗arx(θ2)+atx(θ1)⊗arx(θ1)(13)\mathbf{a}{tx}(\theta_1) \otimes \mathbf{a}{rx}(\theta_2) + \mathbf{a}{tx}(\theta_2) \otimes \mathbf{a}{rx}(\theta_1) = \mathbf{a}{tx}(\theta_2) \otimes \mathbf{a}{rx}(\theta_2) + \mathbf{a}{tx}(\theta_1) \otimes \mathbf{a}{rx}(\theta_1) \tag{13}atx(θ1)⊗arx(θ2)+atx(θ2)⊗arx(θ1)=atx(θ2)⊗arx(θ2)+atx(θ1)⊗arx(θ1)(13)
5. 提出的多径抑制方法
5.1 路径匹配算法原理
路径匹配算法利用二维导向向量a(ϕ,ψ)=atx(ϕ)⊗arx(ψ)\mathbf{a}(\phi, \psi) = \mathbf{a}{tx}(\phi) \otimes \mathbf{a}{rx}(\psi)a(ϕ,ψ)=atx(ϕ)⊗arx(ψ),其中ϕ\phiϕ和ψ\psiψ分别代表AoD和AoA。二维角度谱表示为:
P(ϕ,ψ)=1aH(ϕ,ψ)R−1a(ϕ,ψ)(16)P(\phi, \psi) = \frac{1}{\mathbf{a}^H(\phi, \psi)\mathbf{R}^{-1}\mathbf{a}(\phi, \psi)} \tag{16}P(ϕ,ψ)=aH(ϕ,ψ)R−1a(ϕ,ψ)1(16)
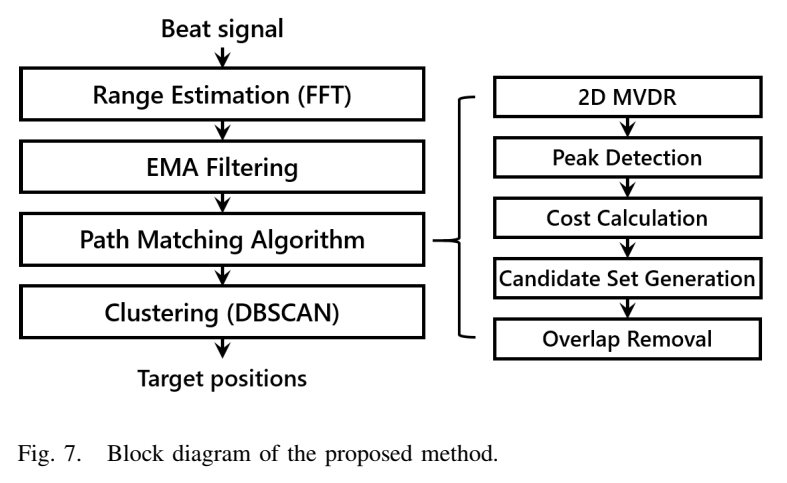
图7描述:图7展示了提出方法的框图。在通过FFT估计距离后,应用指数移动平均(EMA)滤波进行杂波抑制。然后对每个距离单元应用提出的路径匹配算法来检测直接路径并抑制多径。使用DBSCAN算法对检测到的直接路径位置进行聚类以获得最终目标位置。
5.2 EMA滤波实现
为了去除静态背景物体(如周围墙壁和地面)反射的杂波信号,应用EMA滤波。第iii帧的杂波图C(i)\mathbf{C}^{(i)}C(i)和去杂波数据xˉ(i)\bar{\mathbf{x}}^{(i)}xˉ(i)通过以下方式获得:
C(i)={x(i),i=0αC(i−1)+(1−α)x(i),i=1,2,...(14)\mathbf{C}^{(i)} = \begin{cases} \mathbf{x}^{(i)}, & i = 0 \\ \alpha\mathbf{C}^{(i-1)} + (1-\alpha)\mathbf{x}^{(i)}, & i = 1, 2, \ldots \end{cases} \tag{14}C(i)={x(i),αC(i−1)+(1−α)x(i),i=0i=1,2,...(14)
xˉ(i)=x(i)−C(i)(15)\bar{\mathbf{x}}^{(i)} = \mathbf{x}^{(i)} - \mathbf{C}^{(i)} \tag{15}xˉ(i)=x(i)−C(i)(15)
其中α\alphaα是[0,1][0, 1][0,1]范围内的常数。当α\alphaα接近零时,算法更重视近期数据,杂波图更新快;当α\alphaα接近1时,算法更重视历史数据,杂波图更新慢。
5.3 路径匹配算法详细步骤
算法的核心是定义两个代价函数来衡量峰值作为直接路径或多径对的可能性。
直接路径检测 :第lll个峰值作为直接路径的代价函数定义为:
fd(l)=mingfd′(l,g),s.t. g∈[0,1,...,G−1](18)f_d(l) = \min_g f'_d(l, g), \quad \text{s.t. } g \in [0, 1, \ldots, G-1] \tag{18}fd(l)=gminfd′(l,g),s.t. g∈[0,1,...,G−1](18)
其中:
fd′(l,g)=∣AoD[l,g]−AoA[l]∣(19)f'_d(l, g) = |\text{AoD}[l, g] - \text{AoA}[l]| \tag{19}fd′(l,g)=∣AoD[l,g]−AoA[l]∣(19)
它计算第lll个峰值的GGG个可能AoD中的最小代价。当代价小于预定阈值fthrf_{thr}fthr时,第lll条路径被认为是候选直接路径并包含在集合Sd\mathcal{S}_dSd中。
多径对检测 :第lll和lˉ\bar{l}lˉ个峰值(l>lˉl > \bar{l}l>lˉ)作为多径对的代价函数定义为:
fm(l,lˉ)=min(g,gˉ)fm′(l,lˉ,g,gˉ),s.t. g,gˉ∈[0,1,...,G−1](20)f_m(l, \bar{l}) = \min_{(g,\bar{g})} f'_m(l, \bar{l}, g, \bar{g}), \quad \text{s.t. } g, \bar{g} \in [0, 1, \ldots, G-1] \tag{20}fm(l,lˉ)=(g,gˉ)minfm′(l,lˉ,g,gˉ),s.t. g,gˉ∈[0,1,...,G−1](20)
其中:
fm′(l,lˉ,g,gˉ)=12(∣AoD[l,g]−AoA[lˉ]∣+∣AoD[lˉ,gˉ]−AoA[l]∣)(21)f'_m(l, \bar{l}, g, \bar{g}) = \frac{1}{2}\left(|\text{AoD}[l, g] - \text{AoA}[\bar{l}]| + |\text{AoD}[\bar{l}, \bar{g}] - \text{AoA}[l]|\right) \tag{21}fm′(l,lˉ,g,gˉ)=21(∣AoD[l,g]−AoA[lˉ]∣+∣AoD[lˉ,gˉ]−AoA[l]∣)(21)
6. 实验结果与分析
6.1 实验设置
表1 - FMCW雷达规格:
- 载波频率:f0=60f_0 = 60f0=60 GHz
- 调频斜率:S=40S = 40S=40 MHz/μs
- 采样频率:fs=3f_s = 3fs=3 MHz
- 每个调频的采样数:L=256L = 256L=256
- 每帧调频数:M=32M = 32M=32
- 调频扫描时间:Tsw=100T_{sw} = 100Tsw=100 μs
- 调频时间:Tc=200T_c = 200Tc=200 μs
- 帧时间:Tf=50T_f = 50Tf=50 ms
- 发射天线数:Ntx=3N_{tx} = 3Ntx=3
- 接收天线数:Nrx=4N_{rx} = 4Nrx=4
- 发射天线间距:dtx=λd_{tx} = \lambdadtx=λ
- 接收天线间距:drx=λ/2d_{rx} = \lambda/2drx=λ/2
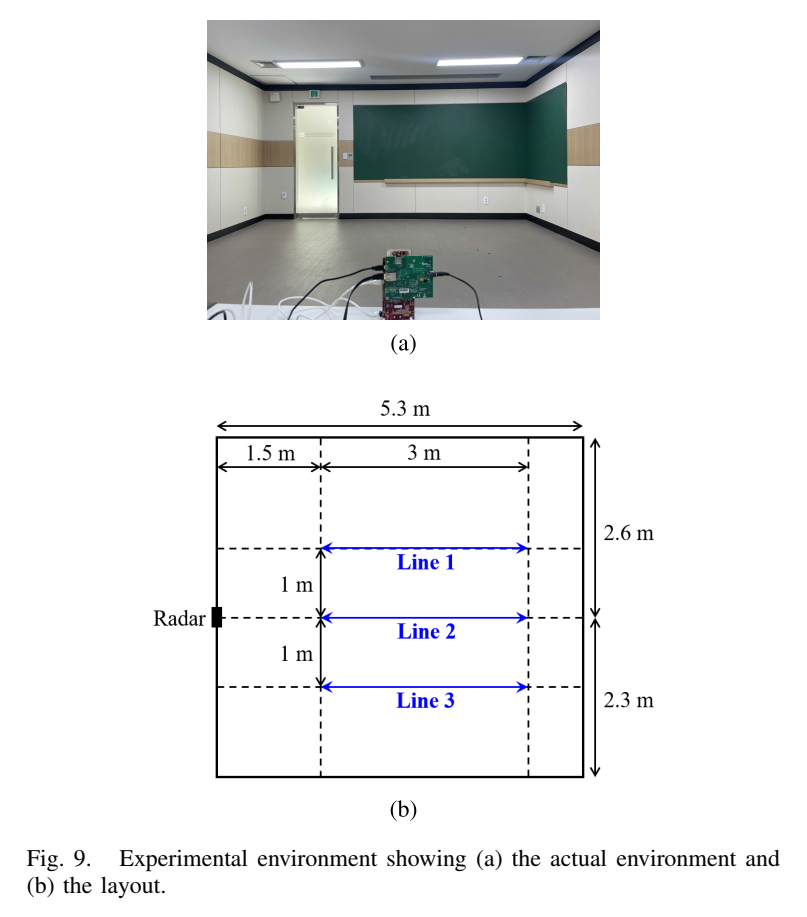
图9描述:图9展示了实验环境,这是一个宽4.9米、深5.3米的典型室内环境。测量期间,人体目标沿图9(b)中表示的线路行走。雷达位于房间一侧,三条测试路线(线1、线2、线3)平行于雷达布置。
6.2 单目标检测结果
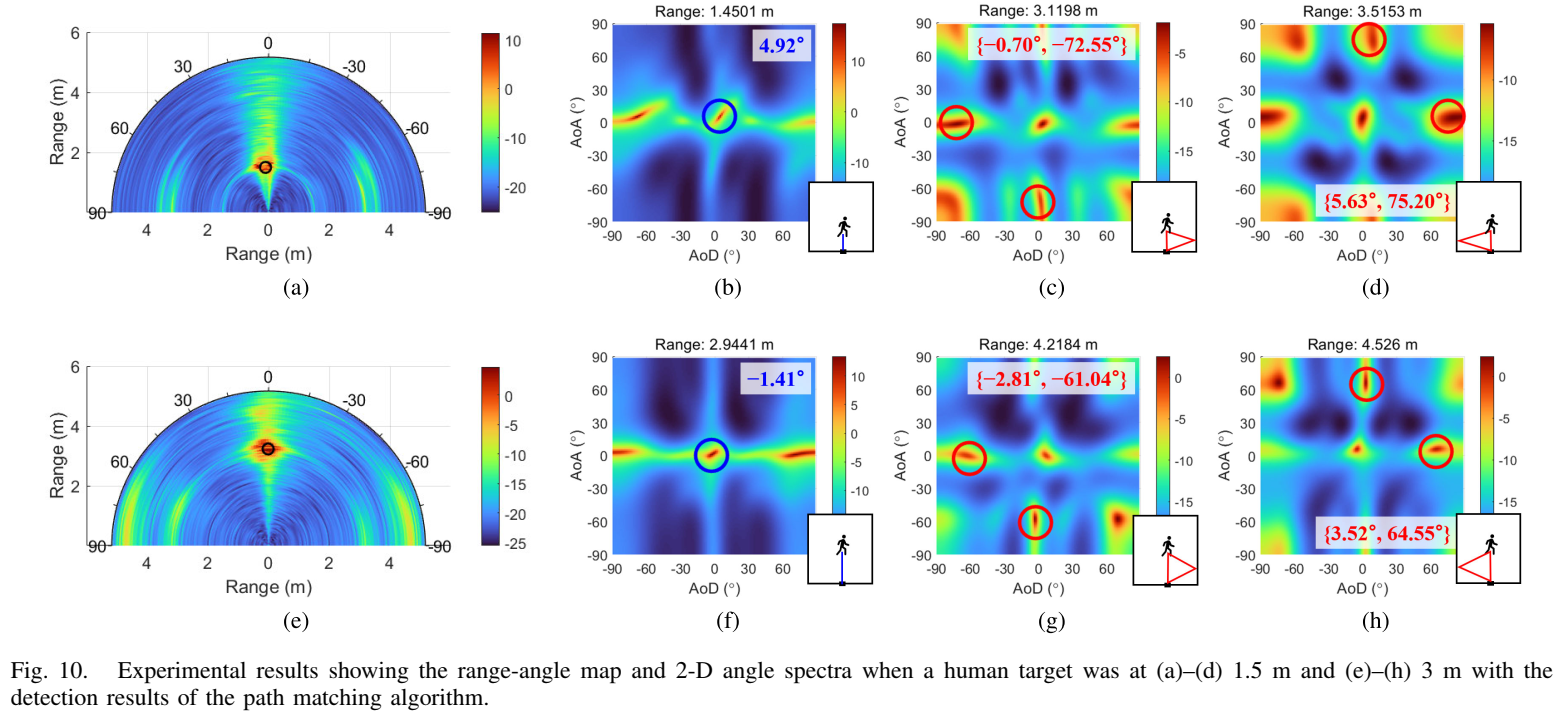
图10描述:图10展示了当人体目标沿线2行走时的实验结果。图10(a)-(d)显示了目标位于1.5米处的数据,图10(e)-(h)显示了目标位于3米处的数据。每组包含距离-角度图和三个二维角度谱。蓝色圆圈表示检测到的直接路径,红色圆圈表示检测到的多径对。
当目标在1.5米处时,直接路径在4.92°被检测到,一阶多径对在{−0.70°,−72.55°}\{-0.70°, -72.55°\}{−0.70°,−72.55°}和{5.63°,75.20°}\{5.63°, 75.20°\}{5.63°,75.20°}被检测到。这些多径对对应于从左侧或右侧墙壁反射的信号路径。当目标在3米处时,直接路径在-1.41°被检测到,多径对在{−2.81°,−61.04°}\{-2.81°, -61.04°\}{−2.81°,−61.04°}和{3.52°,64.55°}\{3.52°, 64.55°\}{3.52°,64.55°}被检测到。
6.3 双目标检测结果
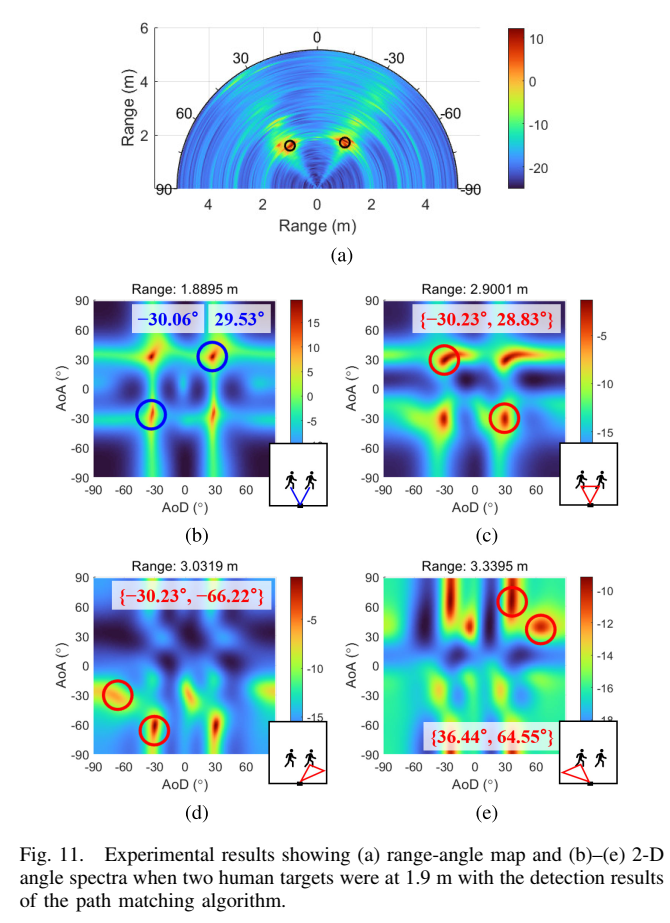
图11描述 :图11展示了两个人体目标分别沿线1和线3行走时的实验结果。图11(a)是距离-角度图,图11(b)-(e)是二维角度谱和检测结果。两个人体目标的直接路径分别在-30.06°和29.53°被检测到。此外,检测到了在两个人体目标之间反射的一阶多径对{−30.23°,28.83°}\{-30.23°, 28.83°\}{−30.23°,28.83°},以及从两侧墙壁反射的多径对{−30.23°,−66.22°}\{-30.23°, -66.22°\}{−30.23°,−66.22°}和{36.44°,64.55°}\{36.44°, 64.55°\}{36.44°,64.55°}。
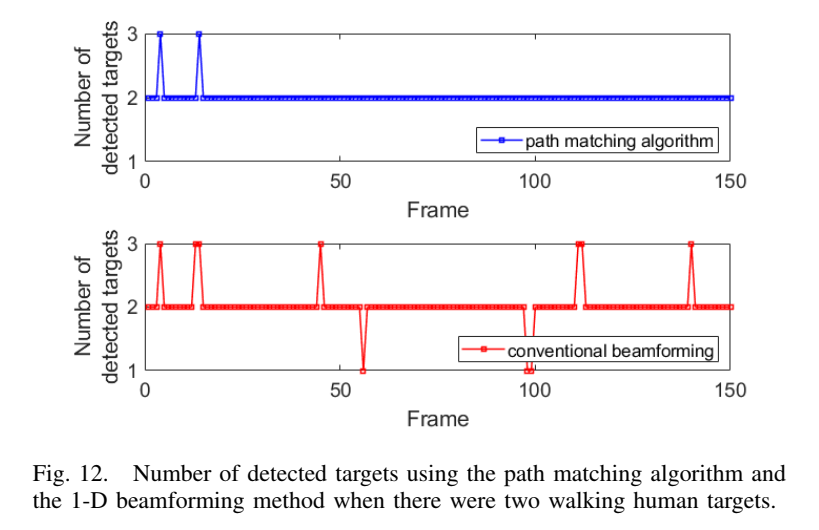
图12描述:图12显示了当两个人体目标行走时150帧期间检测到的目标数量。路径匹配算法(蓝色)相比传统波束形成方法(红色)实现了更稳定的检测性能,虚假目标和漏检目标更少。
6.4 统计性能评估
性能评估使用多目标跟踪准确度(MOTA)指标:
MOTA=1−∑i=0Nf−1(gi+mi+mmei)∑i=0Nf−1hi(24)\text{MOTA} = 1 - \frac{\sum_{i=0}^{N_f-1}(g_i + m_i + mme_i)}{\sum_{i=0}^{N_f-1}h_i} \tag{24}MOTA=1−∑i=0Nf−1hi∑i=0Nf−1(gi+mi+mmei)(24)
其中NfN_fNf是帧数,hih_ihi是第iii帧中的真实人体目标数,gig_igi、mim_imi和mmeimme_immei分别是第iii帧中的虚假目标、漏检目标和错配目标数。
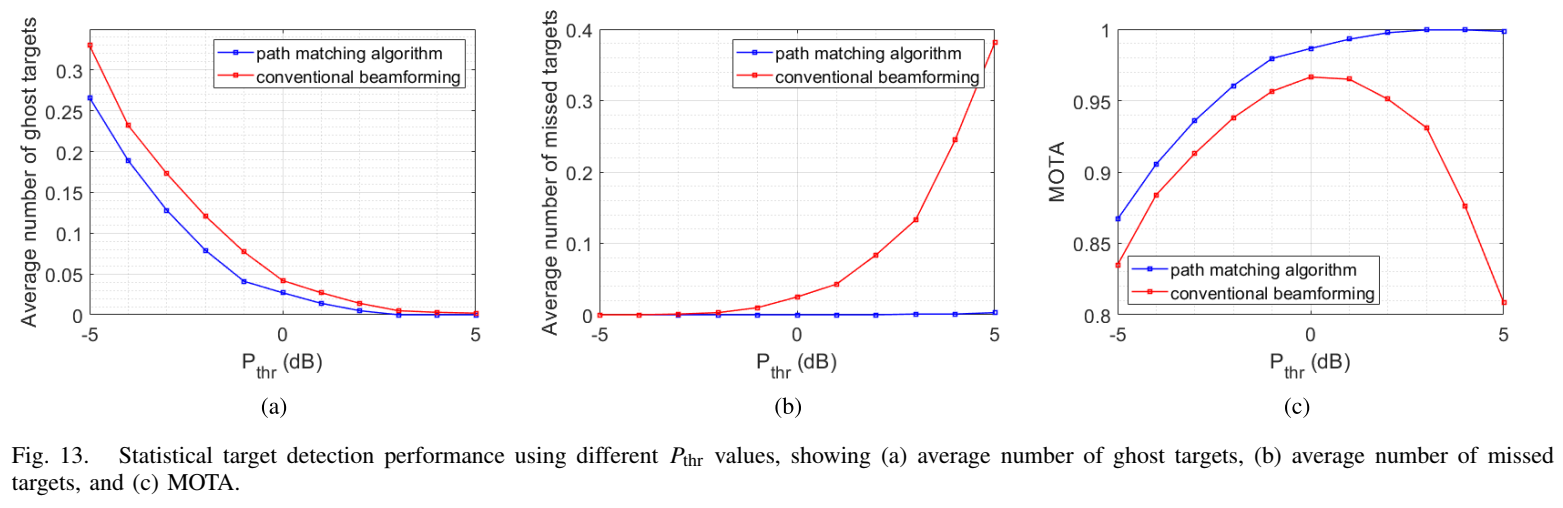
图13描述 :图13显示了不同PthrP_{thr}Pthr值下的统计目标检测性能。当PthrP_{thr}Pthr从-5 dB变化到5 dB时,路径匹配算法在所有PthrP_{thr}Pthr值下都比传统波束形成产生更少的平均虚假目标数。路径匹配算法的平均漏检目标数几乎为零,而传统波束形成存在显著的漏检。当Pthr=4P_{thr} = 4Pthr=4 dB时,路径匹配算法实现了MOTA = 1.000。
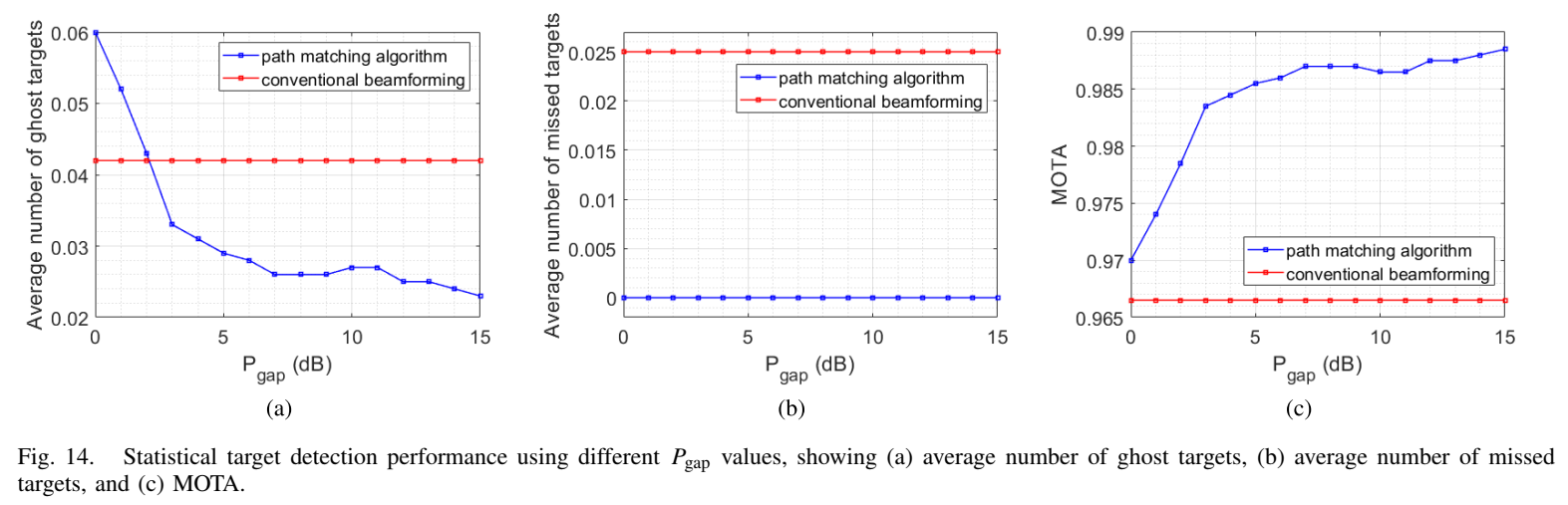
图14描述 :图14显示了不同PgapP_{gap}Pgap值(0到15 dB)下的性能。当Pgap>2P_{gap} > 2Pgap>2 dB时,路径匹配算法成功检测和抑制多径对,导致虚假目标数少于传统波束形成。PgapP_{gap}Pgap应设置为足够大的值以确保有效的多径抑制性能。
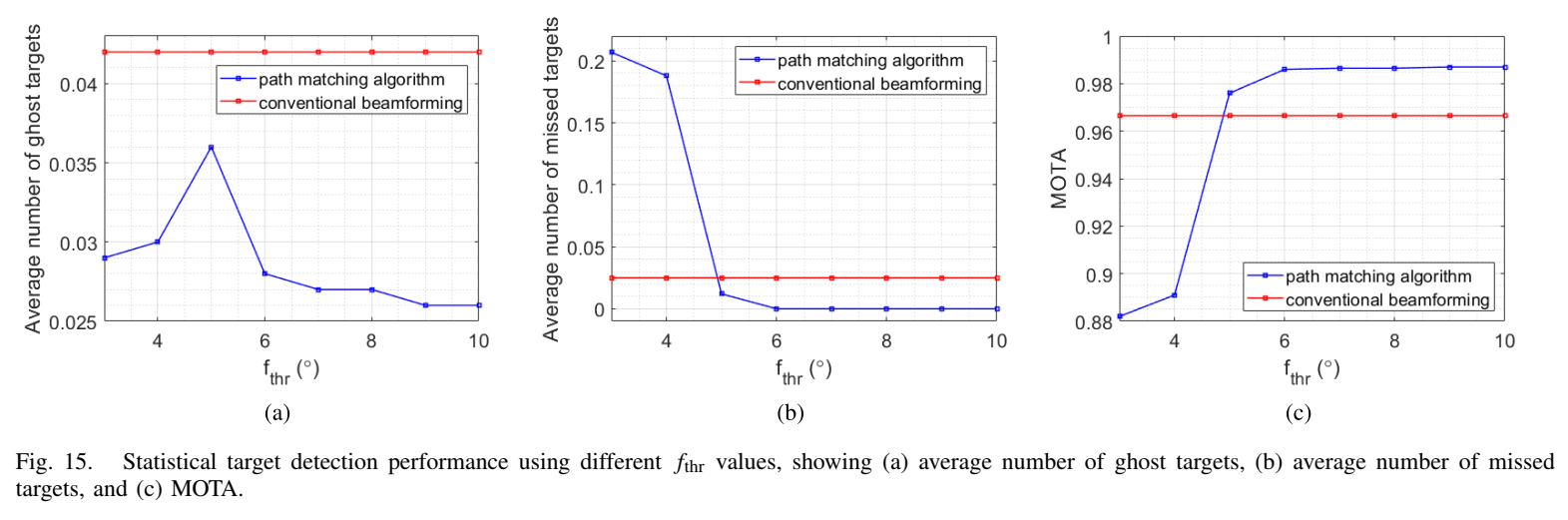
图15描述 :图15显示了不同fthrf_{thr}fthr值(3°到10°)下的性能。路径匹配算法在所有fthrf_{thr}fthr值下都产生更少的虚假目标。当fthr≥5°f_{thr} \geq 5°fthr≥5°时,路径匹配算法的漏检目标更少。fthrf_{thr}fthr应适当选择以容忍考虑硬件和噪声特性的角度失准。
附录:数学推导
A. 虚拟天线阵列的角度谱推导
对于Ntx×NrxN_{tx} \times N_{rx}Ntx×Nrx的MIMO天线阵列,虚拟天线阵列的概念基于发射和接收天线阵列导向向量的Kronecker积。设发射天线阵列的导向向量为:
atx(ϕ)=[1,ej2πdtxsinϕ/λ,...,ej2π(Ntx−1)dtxsinϕ/λ]T\mathbf{a}{tx}(\phi) = [1, e^{j2\pi d{tx}\sin\phi/\lambda}, \ldots, e^{j2\pi(N_{tx}-1)d_{tx}\sin\phi/\lambda}]^Tatx(ϕ)=[1,ej2πdtxsinϕ/λ,...,ej2π(Ntx−1)dtxsinϕ/λ]T
接收天线阵列的导向向量为:
arx(ψ)=[1,ej2πdrxsinψ/λ,...,ej2π(Nrx−1)drxsinψ/λ]T\mathbf{a}{rx}(\psi) = [1, e^{j2\pi d{rx}\sin\psi/\lambda}, \ldots, e^{j2\pi(N_{rx}-1)d_{rx}\sin\psi/\lambda}]^Tarx(ψ)=[1,ej2πdrxsinψ/λ,...,ej2π(Nrx−1)drxsinψ/λ]T
虚拟天线阵列的导向向量通过Kronecker积获得:
av(θ)=atx(θ)⊗arx(θ)\mathbf{a}v(\theta) = \mathbf{a}{tx}(\theta) \otimes \mathbf{a}_{rx}(\theta)av(θ)=atx(θ)⊗arx(θ)
展开后得到长度为NtxNrxN_{tx}N_{rx}NtxNrx的向量:
av(θ)=[atx,0arx,0,atx,0arx,1,...,atx,0arx,Nrx−1,atx,1arx,0,...,atx,Ntx−1arx,Nrx−1]T\mathbf{a}v(\theta) = [a{tx,0}a_{rx,0}, a_{tx,0}a_{rx,1}, \ldots, a_{tx,0}a_{rx,N_{rx}-1}, a_{tx,1}a_{rx,0}, \ldots, a_{tx,N_{tx}-1}a_{rx,N_{rx}-1}]^Tav(θ)=[atx,0arx,0,atx,0arx,1,...,atx,0arx,Nrx−1,atx,1arx,0,...,atx,Ntx−1arx,Nrx−1]T
B. 角度模糊性的数学分析
当天线间距大于λ/2\lambda/2λ/2时,会产生角度模糊。对于间距为d=Gλ/2d = G\lambda/2d=Gλ/2的天线阵列,导向向量的第nnn个元素为:
an(θ)=exp(j2πnGλ2sinθλ)=exp(jπnGsinθ)a_n(\theta) = \exp\left(j2\pi n \frac{G\lambda}{2} \frac{\sin\theta}{\lambda}\right) = \exp(j\pi nG\sin\theta)an(θ)=exp(j2πn2Gλλsinθ)=exp(jπnGsinθ)
由于复指数的2π2\pi2π周期性,当两个角度θ1\theta_1θ1和θ2\theta_2θ2满足:
nGsinθ1=nGsinθ2+2πmnG\sin\theta_1 = nG\sin\theta_2 + 2\pi mnGsinθ1=nGsinθ2+2πm
对于某个整数mmm时,它们产生相同的导向向量元素。这导致:
sinθ2=sinθ1+2mnG\sin\theta_2 = \sin\theta_1 + \frac{2m}{nG}sinθ2=sinθ1+nG2m
对于所有n=1,2,...,N−1n = 1, 2, \ldots, N-1n=1,2,...,N−1,要使上式成立,需要:
sinθ2=sinθ1+2gG\sin\theta_2 = \sin\theta_1 + \frac{2g}{G}sinθ2=sinθ1+G2g
其中ggg是整数。考虑到∣sinθ∣≤1|\sin\theta| \leq 1∣sinθ∣≤1的约束,模糊角度为:
θg=arcsin[mod(sinθ0+2gG+1,2)−1]\theta_g = \arcsin\left[\text{mod}\left(\sin\theta_0 + \frac{2g}{G} + 1, 2\right) - 1\right]θg=arcsin[mod(sinθ0+G2g+1,2)−1]
C. 代价函数的几何解释
直接路径的代价函数fd(l)f_d(l)fd(l)测量二维角度谱中峰值到对角线ϕ=ψ\phi = \psiϕ=ψ的距离。在理想情况下,直接路径应该满足ϕ=ψ\phi = \psiϕ=ψ,因此代价函数:
fd(l)=ming∣AoD[l,g]−AoA[l]∣f_d(l) = \min_g |\text{AoD}[l,g] - \text{AoA}[l]|fd(l)=gmin∣AoD[l,g]−AoA[l]∣
几何上表示峰值到对角线的垂直距离。
对于多径对,两个峰值应该关于对角线镜像对称。设两个峰值的坐标为(ϕ1,ψ1)(\phi_1, \psi_1)(ϕ1,ψ1)和(ϕ2,ψ2)(\phi_2, \psi_2)(ϕ2,ψ2),镜像条件要求:
ϕ1=ψ2,ψ1=ϕ2\phi_1 = \psi_2, \quad \psi_1 = \phi_2ϕ1=ψ2,ψ1=ϕ2
因此多径对的代价函数:
fm(l,lˉ)=12(∣ϕl−ψlˉ∣+∣ϕlˉ−ψl∣)f_m(l, \bar{l}) = \frac{1}{2}(|\phi_l - \psi_{\bar{l}}| + |\phi_{\bar{l}} - \psi_l|)fm(l,lˉ)=21(∣ϕl−ψlˉ∣+∣ϕlˉ−ψl∣)
测量两个峰值偏离理想镜像位置的程度。
D. 协方差矩阵估计与空间平滑
协方差矩阵R=E[xxH]\mathbf{R} = E[\mathbf{x}\mathbf{x}^H]R=E[xxH]在实际中通过样本协方差矩阵估计。为了去相关相干信号源,采用空间平滑技术。将NNN元天线阵列划分为NspN_{sp}Nsp个重叠的子阵列,第kkk个子阵列的数据向量为:
xk=[xk,xk+1,...,xk+L−1]T\mathbf{x}k = [x_k, x{k+1}, \ldots, x_{k+L-1}]^Txk=[xk,xk+1,...,xk+L−1]T
其中L=N−Nsp+1L = N - N_{sp} + 1L=N−Nsp+1是子阵列大小。前向空间平滑的协方差矩阵为:
Rf=1Nsp∑k=0Nsp−1xkxkH\mathbf{R}f = \frac{1}{N{sp}}\sum_{k=0}^{N_{sp}-1}\mathbf{x}_k\mathbf{x}_k^HRf=Nsp1k=0∑Nsp−1xkxkH
前向-后向空间平滑结合了前向和后向子阵列:
R=12(Rf+JRf∗J)\mathbf{R} = \frac{1}{2}(\mathbf{R}_f + \mathbf{JR}_f^*\mathbf{J})R=21(Rf+JRf∗J)
其中J\mathbf{J}J是反对角矩阵,其反对角元素为1。这种技术能够有效去相关相干信号,提高角度估计性能。