前言:
**SCI精读是一项高投入、高回报的科研投资。 它初期看似缓慢,但从长远看,它是构建你深厚学术功底、敏锐科研嗅觉和强大创新能力的唯一捷径。将精读养成习惯,它最终会从一项"任务"变成一种能带给你巨大成就感和乐趣的"能力",介于此,本Up主开设sci领读课程,旨在让小伙伴们在快乐中快速具备论文写作能力!**本专栏为视频课程中的文章翻译!
用于密集目标检测的焦点损失
Tsung-Yi Lin、Priya Goyal、Ross Girshick、Kaiming He、Piotr Dollár
Facebook人工智能研究院(FAIR)
公式与图表先导
文中核心公式定义如下:
- 交叉熵(Cross Entropy, CE)损失: C E ( p t ) = − log ( p t ) CE(p_t) = -\log(p_t) CE(pt)=−log(pt)
- 焦点损失(Focal Loss, FL): F L ( p t ) = − ( 1 − p t ) γ log ( p t ) FL(p_t) = -(1-p_t)^\gamma \log(p_t) FL(pt)=−(1−pt)γlog(pt)
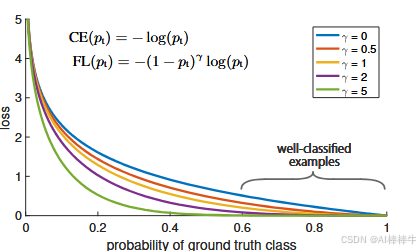
图1 焦点损失曲线示意
图注 :我们提出一种名为"焦点损失(Focal Loss)"的新型损失函数,它在标准交叉熵准则中引入因子 ( 1 − p i ) γ (1-p_i)^\gamma (1−pi)γ。当 γ > 0 \gamma>0 γ>0时,会降低分类良好样本( p t > 0.5 p_t>0.5 pt>0.5)的相对损失权重,从而将训练焦点更多放在难分、误分类样本上。正如后续实验所验证的,在存在大量易分背景样本的场景下,该焦点损失能够支持训练高精度的密集目标检测器。
图2 COCO test-dev数据集上的速度-精度权衡
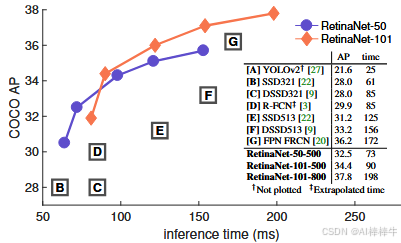
图注:COCO test-dev数据集上的速度(毫秒)与精度(AP)对比。在焦点损失的支持下,我们提出的简单单阶段检测器"视网膜网络(RetinaNet)"性能超过了所有现有单阶段和两阶段检测器,包括文献[20]中报道的最优Faster R-CNN系统[28]。图中展示了基于ResNet-50-FPN(蓝色圆形)和ResNet-101-FPN(橙色菱形)的RetinaNet变体,涵盖5种输入尺度(400-800像素)。若忽略低精度区间(AP<25),RetinaNet构成了当前所有检测器的"性能上包络线";其改进变体(未绘图)的AP可达40.8。详细结果见第5节。
摘要
迄今为止,精度最高的目标检测器基于由R-CNN(区域卷积神经网络)推广的两阶段方法 :先生成稀疏的候选目标位置,再对这些位置进行分类。相比之下,单阶段检测器 通过在图像上规则、密集地采样候选目标位置实现检测,理论上具备更快的速度和更简洁的结构,但精度始终落后于两阶段检测器。本文探究了这一差距的根源,发现:密集检测器训练过程中存在的极端前景-背景类别不平衡是核心原因。
为解决该类别不平衡问题,我们对标准交叉熵损失进行"重塑",降低分类良好样本的损失权重。我们提出的焦点损失 能将训练聚焦于稀疏的难分样本,避免大量易分负样本在训练中"主导"模型。为验证该损失的有效性,我们设计并训练了一款简单的密集检测器------视网膜网络(RetinaNet) 。实验结果表明:结合焦点损失训练的RetinaNet,既能达到现有单阶段检测器的速度,又能超越所有已有的最先进两阶段检测器的精度。代码开源地址:https://github.com/facebookresearch/Detectron。
1. 引言
当前最先进的目标检测器均基于"候选区域驱动机制"的两阶段框架。正如R-CNN框架[11]所推广的,第一阶段生成稀疏的候选目标位置,第二阶段通过卷积神经网络将每个候选位置分类为"前景类别"或"背景"。经过一系列技术改进[10,28,20,14],该两阶段框架在具有挑战性的COCO基准数据集[21]上始终保持最高精度。
尽管两阶段检测器性能优异,但一个关键问题亟待解答:简单的单阶段检测器能否达到相近精度?单阶段检测器通过对"目标位置、尺度、宽高比"进行规则、密集的采样实现检测。近年来,YOLO[26,27]、SSD(单次多框检测器)[22,9]等单阶段检测器取得了不错的进展,速度更快,但精度仍比最先进的两阶段方法低10%-40%(相对值)。
本文进一步突破这一局限:我们提出的单阶段目标检测器,首次在COCO数据集的AP(平均精度)指标上,达到了复杂两阶段检测器(如基于Faster R-CNN[28]的特征金字塔网络(FPN)[20]或掩码R-CNN(Mask R-CNN)[14]变体)的水平。为实现这一目标,我们明确了"训练过程中的类别不平衡"是阻碍单阶段检测器达到最高精度的主要障碍,并提出一种新的损失函数消除该障碍。
R-CNN类两阶段检测器通过"两阶段级联"和"采样策略"解决类别不平衡问题:
- 候选区域生成阶段(如选择性搜索[35]、边缘框(EdgeBoxes)[39]、DeepMask[24,25]、区域候选网络(RPN)[28])快速将候选目标位置从海量可能中筛选至少量(如1-2k个),过滤掉大部分背景样本;
- 第二分类阶段通过"固定前景-背景比例(如1:3)"或"在线难样本挖掘(OHEM)[31]"等采样策略,维持前景与背景的平衡。
相比之下,单阶段检测器需处理图像上规则采样的大量候选位置------实际中通常需枚举约10万个位置,覆盖所有空间位置、尺度和宽高比。尽管可采用类似的采样策略,但训练过程仍会被"易分背景样本"主导,效率极低。这种低效是目标检测中的经典问题,传统上通过"自举(bootstrapping)[33,29]"或"难样本挖掘[37,8,31]"等技术缓解。
本文提出一种新的损失函数,作为解决类别不平衡问题的更优方案。该损失函数是"动态缩放的交叉熵损失":当模型对正确类别的置信度越高时,缩放因子越趋近于0(见图1)。直观来看,该缩放因子能在训练中自动降低易分样本的贡献,快速将模型注意力聚焦于难分样本。实验表明,我们提出的焦点损失能支持训练高精度单阶段检测器,其性能显著优于基于"采样策略"或"难样本挖掘"的现有单阶段检测器训练方法。最后需说明:焦点损失的具体形式并非唯一关键,我们将证明其他变体也能实现相近效果。
为验证焦点损失的有效性,我们设计了一款简单的单阶段目标检测器------RetinaNet(视网膜网络) ,其命名源于对输入图像中目标位置的"密集采样"特性。该检测器融合了"网络内高效特征金字塔"和"锚框(anchor boxes)"设计,借鉴了[22,6,28,20]中的多项最新技术。RetinaNet兼具效率与精度:基于ResNet-101-FPN骨干网络的最优模型,在COCO test-dev数据集上的AP达39.1,同时推理速度为5帧/秒(fps),性能超过了所有已发表的单阶段和两阶段检测器的单模型结果(见图2)。
2. 相关工作
2.1 经典目标检测器
"滑动窗口范式"(在密集图像网格上应用分类器)具有悠久历史:LeCun等人[19,36]最早将卷积神经网络用于手写数字识别,开启了该范式的成功实践;Viola和Jones[37]提出"提升目标检测器"用于人脸检测,推动此类模型的广泛应用;方向梯度直方图(HOG)[4]和积分通道特征[5]的提出,为行人检测提供了有效方法;可变形部件模型(DPMs)[8]将密集检测器扩展到更通用的目标类别,曾在多年内保持PASCAL数据集[7]的最优性能。尽管滑动窗口是经典计算机视觉中的主流检测范式,但随着深度学习[18]的复兴,下文中的"两阶段检测器"迅速主导了目标检测领域。
2.2 两阶段检测器
现代目标检测的主流范式是"两阶段方法":
- 第一阶段生成稀疏的候选区域(需包含所有目标,同时过滤大部分负样本),如选择性搜索[35];
- 第二阶段将候选区域分类为"前景类别"或"背景"。
R-CNN[11]将第二阶段分类器升级为卷积网络,大幅提升精度,开启了现代目标检测时代。此后,R-CNN在速度[15,10]和"学习式候选区域生成"[6,24,28]方面不断优化:区域候选网络(RPN)将"候选区域生成"与"第二阶段分类"整合到单一卷积网络中,形成Faster R-CNN框架[28]。该框架还衍生出众多扩展版本[20,31,32,16,14]。
2.3 单阶段检测器
OverFeat[30]是最早基于深度网络的现代单阶段检测器之一。近年来,SSD[22,9]和YOLO[26,27]重新激发了对单阶段方法的关注:这些检测器以"速度优化"为目标,但精度始终落后于两阶段方法------SSD的AP比两阶段方法低10%-20%,YOLO则更侧重"极端速度-精度权衡"(见图2)。
近期研究[17]表明:通过降低输入图像分辨率和候选区域数量,两阶段检测器可实现快速推理;但即便给予更大的计算预算,单阶段方法的精度仍落后。相比之下,本文的目标是验证:单阶段检测器能否在"速度与两阶段方法相当或更快"的前提下,达到甚至超越两阶段方法的精度。
RetinaNet的设计与现有密集检测器有诸多相似之处,尤其借鉴了RPN[28]的"锚框"概念,以及SSD[22]和FPN[20]的"特征金字塔"思想。需强调的是:该简单检测器之所以能达到最优性能,并非依赖网络设计创新,而是源于我们提出的新型损失函数。
2.4 类别不平衡问题
无论是经典单阶段检测器(如提升检测器[37,5]、DPMs[8]),还是现代方法(如SSD[22]),训练过程中均面临严重的类别不平衡:每幅图像需评估10⁴-10⁵个候选位置,但仅少数位置包含目标。这种不平衡会导致两个问题:
- 训练效率低:大部分易分负样本无法提供有效学习信号;
- 模型退化:大量易分负样本的累积损失会"主导"训练过程。
传统解决方案是"难负样本挖掘"[33,37,8,31,22](训练中仅采样难分样本)或更复杂的"采样/重加权策略"[2]。相比之下,我们提出的焦点损失能自然应对单阶段检测器的类别不平衡问题,支持在"不采样"的情况下高效训练所有样本,且不会出现"易分负样本主导损失和梯度"的现象。
2.5 鲁棒估计
学界对"鲁棒损失函数"(如胡贝尔损失(Huber loss)[13])的研究较多,这类函数通过降低"大误差样本(难样本)"的损失权重来减少异常值影响。与之相反,焦点损失的目标并非处理异常值,而是通过降低"内点(易分样本)"的损失权重来解决类别不平衡------本质上,焦点损失与鲁棒损失的作用相反:它将训练聚焦于稀疏的难样本。
3. 焦点损失
焦点损失旨在解决"单阶段目标检测训练中的极端前景-背景类别不平衡"问题(如类别比例1:1000)。我们从二分类交叉熵损失出发,逐步推导焦点损失的定义。
3.1 交叉熵损失(基础)
二分类交叉熵(CE)损失定义为:
C E ( p , y ) = { − log ( p ) 若 y = 1 − log ( 1 − p ) 否则 (1) CE(p,y)=\begin{cases} -\log(p) & \text{若 } y=1 \\ -\log(1-p) & \text{否则} \end{cases} \tag{1} CE(p,y)={−log(p)−log(1−p)若 y=1否则(1)
其中:
- y ∈ { ± 1 } y \in \{±1\} y∈{±1} 表示真实类别(1为前景,-1为背景);
- p ∈ [ 0 , 1 ] p \in [0,1] p∈[0,1] 表示模型对" y = 1 y=1 y=1类"的估计概率。
为简化符号,定义 p t p_t pt:
p t = { p 若 y = 1 1 − p 否则 p_t=\begin{cases} p & \text{若 } y=1 \\ 1-p & \text{否则} \end{cases} pt={p1−p若 y=1否则
则交叉熵损失可重写为: C E ( p , y ) = C E ( p t ) = − log ( p t ) CE(p,y)=CE(p_t)=-\log(p_t) CE(p,y)=CE(pt)=−log(pt)。
如第1节图1所示,交叉熵损失的蓝色(上方)曲线具有一个显著特性:即使是易分样本( p t ≫ 0.5 p_t \gg 0.5 pt≫0.5),也会产生"不可忽视的损失值"。当大量易分样本的损失累积时,会"淹没"少数前景样本的损失信号。
3.2 平衡交叉熵
解决类别不平衡的常用方法是引入"权重因子":对"1类"(前景)赋予权重 α ∈ [ 0 , 1 ] \alpha \in [0,1] α∈[0,1],对"-1类"(背景)赋予权重 1 − α 1-\alpha 1−α。实际应用中, α \alpha α可通过"类别频率的倒数"设定,或作为超参数通过交叉验证优化。
为简化符号,类比 p t p_t pt定义 α t \alpha_t αt(对"1类"取 α \alpha α,对"-1类"取 1 − α 1-\alpha 1−α),则平衡交叉熵损失 可表示为:
C E ( p t ) = − α t log ( p t ) (3) CE(p_t) = -\alpha_t \log(p_t) \tag{3} CE(pt)=−αtlog(pt)(3)
该损失是交叉熵的简单扩展,将作为后续焦点损失的实验基线。
3.3 焦点损失定义
实验表明:密集检测器训练中的"极端类别不平衡"会彻底"主导"交叉熵损失------易分负样本的损失占比极高,且主导梯度更新。尽管 α \alpha α能平衡前景与背景的损失权重,但无法区分"易分样本"与"难分样本"。为此,我们提出对损失函数进行"重塑",通过降低易分样本的权重,将训练焦点集中在难分负样本上。
更正式地,我们在交叉熵损失中引入调制因子 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ ( γ ≥ 0 \gamma ≥0 γ≥0为可调节的"聚焦参数"),由此定义焦点损失 :
F L ( p t ) = − ( 1 − p t ) γ log ( p t ) (4) FL(p_t) = -(1-p_t)^\gamma \log(p_t) \tag{4} FL(pt)=−(1−pt)γlog(pt)(4)
焦点损失的核心特性(见图1)
- 难分样本损失无衰减 :当样本被误分类( p t p_t pt较小时),调制因子 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ接近1,损失与交叉熵基本一致;当样本分类置信度提升( p t → 1 p_t \to 1 pt→1),调制因子趋近于0,易分样本的损失被大幅降低。
- 聚焦强度可调节 :聚焦参数 γ \gamma γ能平滑调节"易分样本损失的衰减速率":
- 当 γ = 0 \gamma=0 γ=0时,焦点损失退化为交叉熵损失;
- 随着 γ \gamma γ增大,调制因子的"衰减效应"增强(实验中发现 γ = 2 \gamma=2 γ=2时效果最优)。
直观理解
调制因子的核心作用是"降低易分样本的损失贡献,并扩大'低损失样本'的覆盖范围"。例如,当 γ = 2 \gamma=2 γ=2时:
- 对于 p t = 0.9 p_t=0.9 pt=0.9的易分样本,其损失仅为交叉熵损失的 1 % 1\% 1%( ( 1 − 0.9 ) 2 = 0.01 (1-0.9)^2=0.01 (1−0.9)2=0.01);
- 对于 p t ≈ 0.968 p_t≈0.968 pt≈0.968的易分样本,其损失仅为交叉熵损失的 0.1 % 0.1\% 0.1%( ( 1 − 0.968 ) 2 ≈ 0.001 (1-0.968)^2≈0.001 (1−0.968)2≈0.001)。
与此同时,误分类样本(如 p t ≤ 0.5 p_t≤0.5 pt≤0.5)的损失衰减幅度最大不超过4倍(当 p t = 0.5 p_t=0.5 pt=0.5时, ( 1 − 0.5 ) 2 = 0.25 (1-0.5)^2=0.25 (1−0.5)2=0.25),这使得"修正误分类样本"的重要性显著提升。
实际应用:α-平衡焦点损失
在实际实验中,我们采用"α-平衡"版本的焦点损失,能进一步提升精度:
F L ( p t ) = − α t ( 1 − p t ) γ log ( p t ) (5) FL(p_t) = -\alpha_t (1-p_t)^\gamma \log(p_t) \tag{5} FL(pt)=−αt(1−pt)γlog(pt)(5)
此外,损失层的实现中,我们将"计算 p p p的sigmoid操作"与"损失计算"整合,以提升数值稳定性。
(注:焦点损失可直接扩展到多分类场景,效果良好;为简化表述,本文聚焦二分类损失。)
3.4 类别不平衡与模型初始化
二分类模型默认初始化时,对" y = 1 y=1 y=1"和" y = − 1 y=-1 y=−1"的输出概率相等(均为0.5)。在类别不平衡场景下,这种初始化会导致"多数类(背景)的损失主导总损失",引发训练初期的不稳定性。
为解决该问题,我们引入"模型初始化先验概率":对"少数类(前景)"的初始估计概率 p p p设定一个较小的先验值 π \pi π(如 π = 0.01 \pi=0.01 π=0.01)。需强调的是,这是"模型初始化的调整"(见4.1节),而非损失函数的修改。实验表明,该策略能显著提升"交叉熵损失"和"焦点损失"在极端类别不平衡场景下的训练稳定性。
3.5 类别不平衡与两阶段检测器
两阶段检测器通常直接使用交叉熵损失,无需α-平衡或焦点损失,其通过两种机制解决类别不平衡:
- 两阶段级联:候选区域生成机制[35,24,28]将"海量可能的目标位置"筛选至1-2k个候选区域,且这些候选区域大概率对应真实目标,从而过滤掉绝大多数易分负样本;
- 有偏小批量采样:第二阶段训练时,通过"有偏采样"构建小批量样本(如前景-背景比例1:3),该比例相当于"隐含的α-平衡因子",通过采样实现类别平衡。
我们提出的焦点损失,本质是通过"损失函数设计",直接在单阶段检测系统中实现上述两阶段机制的效果。
4. 视网膜网络(RetinaNet)检测器
RetinaNet是一个"统一的单网络结构",由"骨干网络"和"两个任务特定子网络"组成:
- 骨干网络:对整幅输入图像计算卷积特征图,采用"现成的卷积网络"实现;
- 分类子网络:基于骨干网络的输出,执行卷积式目标分类;
- 回归子网络:基于骨干网络的输出,执行卷积式边界框回归。
两个子网络的设计简洁,专为"单阶段密集检测"优化(见图3)。实验表明,该检测器的多数设计参数对"精确值不敏感",下文将详细介绍各组件。
4.1 特征金字塔网络(FPN)骨干
RetinaNet采用文献[20]提出的特征金字塔网络(Feature Pyramid Network, FPN) 作为骨干网络。简言之,FPN在标准卷积网络基础上,增加"自上而下路径"和"横向连接",能从"单一分辨率输入图像"中高效构建"丰富的多尺度特征金字塔"(见图3(a)-(b))。金字塔的每个层级可用于检测不同尺度的目标。
FPN能显著提升全卷积网络(FCN)[23]的多尺度预测能力,这一点已在RPN[28]、DeepMask风格候选区域[24]及Fast R-CNN[10]、Mask R-CNN[14]等两阶段检测器中得到验证。
FPN的具体实现(基于ResNet)
遵循文献[20],我们在ResNet架构[16]基础上构建FPN,生成 P 3 P_3 P3至 P 7 P_7 P7的金字塔层级( l l l表示层级, P l P_l Pl的分辨率为输入图像的 1 / 2 l 1/2^l 1/2l)。所有金字塔层级均包含256个通道( C = 256 C=256 C=256),实现细节基本遵循[20],仅做少量调整以平衡速度与精度:
- 为降低计算量,未使用高分辨率层级 P 2 P_2 P2;
- P 6 P_6 P6通过对 C 5 C_5 C5(ResNet的第5个残差阶段输出)执行"3×3步长为2的卷积"生成(而非下采样);
- 增加 P 7 P_7 P7层级:对 P 6 P_6 P6先执行ReLU激活,再执行"3×3步长为2的卷积",以提升大目标检测精度。
初步实验表明:仅使用ResNet最后一层特征的检测器AP极低,因此FPN骨干网络对RetinaNet至关重要。
4.2 锚框(Anchors)
RetinaNet采用与文献[20]中RPN变体相似的"平移不变锚框",具体设计如下:
- 尺度覆盖 :金字塔层级 P 3 P_3 P3至 P 7 P_7 P7对应的锚框面积分别为 3 2 2 32^2 322至 51 2 2 512^2 5122(像素),覆盖32-813像素的目标尺度范围(相对于输入图像);
- 宽高比与尺度密度 :每个层级采用3种宽高比{1:2, 1:1, 2:1};为提升尺度覆盖密度,每个层级额外增加"原尺度的 2 0 2^0 20、 2 1 / 3 2^{1/3} 21/3、 2 2 / 3 2^{2/3} 22/3倍"3种尺度,最终每个层级包含9个锚框( A = 9 A=9 A=9)。
锚框与真实框的匹配规则
每个锚框需分配:
- 分类目标 :长度为 K K K(目标类别数)的独热向量(若锚框匹配真实框,则对应类别位置为1,其余为0;若为背景则全为0);
- 回归目标:4维向量(锚框与匹配真实框的偏移量)。
匹配规则基于"交并比(IoU)",并针对多分类场景调整:
- 若锚框与某真实框的IoU≥0.5:匹配该真实框,标记为"前景";
- 若锚框与所有真实框的IoU∈[0, 0.4):标记为"背景";
- 若IoU∈[0.4, 0.5):不参与训练(忽略)。
每个锚框最多匹配一个真实框;若未匹配任何真实框且不属于"忽略区间",则视为背景。
4.3 分类子网络
分类子网络的目标是:对每个空间位置的 A A A个锚框,预测其属于 K K K个目标类别的概率。该子网络是"附加在每个FPN层级上的小型全卷积网络(FCN)",且所有金字塔层级共享子网络参数。
网络结构(见图3©)
输入:某FPN层级的 C C C通道特征图( C = 256 C=256 C=256);
流程:4层"3×3卷积+ReLU激活"(每层均为256个滤波器)→ 1层"3×3卷积"( K × A K×A K×A个滤波器)→ sigmoid激活;
输出:每个空间位置对应 K × A K×A K×A个二值预测(即每个锚框的 K K K个类别概率)。
与RPN[28]相比,该分类子网络的差异在于:层数更深、仅使用3×3卷积、与回归子网络参数不共享------实验表明这些设计对精度提升更关键。
4.4 边界框回归子网络
回归子网络与分类子网络并行,附加在每个FPN层级上,目标是"预测每个锚框到匹配真实框的偏移量"。其结构与分类子网络基本一致,仅输出层不同:
- 输出层为"3×3卷积"( 4 × A 4×A 4×A个滤波器),无激活函数(线性输出);
- 每个空间位置对应 4 × A 4×A 4×A个回归值(即每个锚框的4维偏移量,采用R-CNN[11]的标准边界框参数化方式)。
需注意:该回归子网络是"类别无关的(class-agnostic)"------无需为每个类别单独设计回归器,参数更少且精度相当。分类子网络与回归子网络虽结构相似,但参数完全独立。
4.5 推理与训练细节
推理流程
RetinaNet是"端到端全卷积网络"(含ResNet-FPN骨干、分类子网络、回归子网络,见图3),推理仅需将图像输入网络并执行前向传播,具体步骤:
- 为提升速度,对每个FPN层级,仅保留"置信度≥0.05"的预测框,且每个层级最多保留1000个高得分预测框;
- 合并所有层级的预测框,执行"非极大值抑制(NMS)"(阈值0.5),得到最终检测结果。
焦点损失的训练配置
- 核心参数 :实验发现 γ = 2 \gamma=2 γ=2效果最优,且RetinaNet对 γ ∈ [ 0.5 , 5 ] \gamma \in [0.5,5] γ∈[0.5,5]的鲁棒性较好; α \alpha α需与 γ \gamma γ协同选择( γ \gamma γ增大时 α \alpha α需略减小, γ = 2 \gamma=2 γ=2时 α = 0.25 \alpha=0.25 α=0.25最优)。
- 损失计算范围:训练时,焦点损失应用于所有约10万个锚框(区别于RPN的"启发式采样"或SSD/OHEM的"难样本挖掘"------仅选择256个锚框)。
- 损失归一化:图像的总焦点损失通过"分配到真实框的锚框数量"归一化(而非总锚框数量),因为大量易分负样本在焦点损失下的贡献可忽略不计。
模型初始化
RetinaNet支持ResNet-50-FPN和ResNet-101-FPN两种骨干网络,初始化规则如下:
- 基础ResNet-50/101模型:使用在ImageNet1k数据集上预训练的权重[16];
- FPN新增层:按文献[20]的方式初始化;
- 子网络新增层:除分类子网络的最终卷积层外,其余卷积层均采用"偏置 b = 0 b=0 b=0、权重高斯分布( σ = 0.01 \sigma=0.01 σ=0.01)"初始化;
- 分类子网络最终卷积层:偏置初始化为 b = − log ( ( 1 − π ) / π ) b=-\log((1-\pi)/\pi) b=−log((1−π)/π)( π = 0.01 \pi=0.01 π=0.01),确保训练初期每个锚框的"前景类别置信度"约为 π \pi π,避免大量背景锚框在训练初期产生不稳定的大损失。
优化策略
- 优化器:随机梯度下降(SGD);
- 分布式训练:8块GPU同步训练,总批量大小16(每块GPU处理2幅图像);
- 训练迭代:共9万次迭代,初始学习率0.01,6万次和8万次迭代时分别除以10;
- 数据增强:仅使用"水平图像翻转"(无其他增强);
- 正则化:权重衰减0.0001,动量0.9;
- 总损失:焦点损失(分类)+ 标准平滑L1损失(回归)[10];
- 训练时间:表1e中模型的训练时间为10-35小时。
图3 RetinaNet网络架构
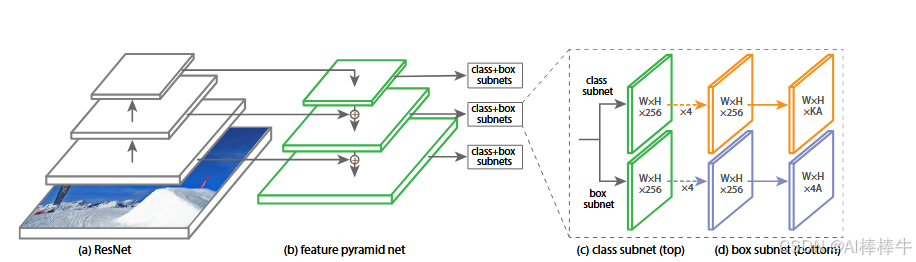
为ResNet骨干网络,(b)为特征金字塔网络(FPN),©为分类子网络(上方),(d)为边界框回归子网络(下方),标注包含"W×H×256""W×H×KA""W×H×4A"等特征图维度信息)
图注:单阶段RetinaNet网络架构以"残差网络(ResNet)[16]"为基础(a),通过"特征金字塔网络(FPN)[20]"生成丰富的多尺度卷积特征金字塔(b)。在该骨干网络之上,RetinaNet附加两个子网络:一个用于锚框分类(c),一个用于锚框到真实框的回归(d)。该网络设计刻意保持简洁,以便本文聚焦于"新型焦点损失"------正是该损失消除了"单阶段检测器与Faster R-CNN(带FPN)[20]等最先进两阶段检测器"的精度差距,同时保持更快的速度。
5. 实验
实验基于COCO目标检测基准数据集[21]的"边界框检测任务",数据集划分与评估方式如下:
- 训练集:trainval35k(合并COCO的8万幅train图像和4万幅val图像中的3.5万幅随机子集);
- 消融实验评估集:minival(val图像中剩余的5千幅,用于超参数调优和消融分析);
- 主结果评估集:test-dev(无公开标签,需通过COCO评估服务器获取AP结果)。
除非特别说明,所有消融实验均采用"ResNet-50-FPN骨干网络"和"600像素输入尺度(训练与测试)"。
5.1 密集检测的训练优化分析
5.1.1 网络初始化的影响
初始尝试使用"标准交叉熵损失+默认初始化"训练RetinaNet时,网络迅速发散;而仅调整"分类子网络最终层的偏置初始化"( π = 0.01 \pi=0.01 π=0.01),即可实现有效学习------基于ResNet-50的模型在COCO数据集上的AP达30.2。实验表明, π \pi π的具体值对结果影响较小,后续实验统一使用 π = 0.01 \pi=0.01 π=0.01。
5.1.2 平衡交叉熵的效果
表1a展示了"α-平衡交叉熵损失"在不同 α \alpha α值下的性能。当 α = 0.75 \alpha=0.75 α=0.75时,模型AP达31.1,较默认交叉熵( α = 0.5 \alpha=0.5 α=0.5时AP=30.2)提升0.9个百分点,验证了"类别平衡"对精度的增益。
5.1.3 焦点损失的效果
表1b展示了焦点损失在不同 γ \gamma γ值下的性能(每个 γ \gamma γ均匹配最优 α \alpha α):
- 当 γ = 0 \gamma=0 γ=0时,焦点损失退化为平衡交叉熵(AP=31.1);
- 随着 γ \gamma γ增大,AP逐步提升, γ = 2 \gamma=2 γ=2时达到最优(AP=34.0),较平衡交叉熵提升2.9个百分点;
- 当 γ > 2 \gamma>2 γ>2(如 γ = 5 \gamma=5 γ=5)时,AP略有下降(32.2),但仍高于平衡交叉熵。
此外, α \alpha α与 γ \gamma γ的协同关系表明: γ \gamma γ增大时, α \alpha α需适当减小(如 γ = 0 \gamma=0 γ=0时 α = 0.75 \alpha=0.75 α=0.75, γ = 2 \gamma=2 γ=2时 α = 0.25 \alpha=0.25 α=0.25)------因为易分负样本的损失已被大幅衰减,无需通过高 α \alpha α过度强调前景样本。
5.1.4 焦点损失的机理分析(图4)
为深入理解焦点损失,我们对"收敛模型"的损失分布进行统计:选取基于ResNet-101、600像素输入、 γ = 2 \gamma=2 γ=2训练的RetinaNet模型(AP=36.0),在大量随机图像上采样约 1 0 7 10^7 107个负样本和 1 0 5 10^5 105个正样本,计算不同 γ \gamma γ值下的"归一化损失累积分布函数(CDF)"。
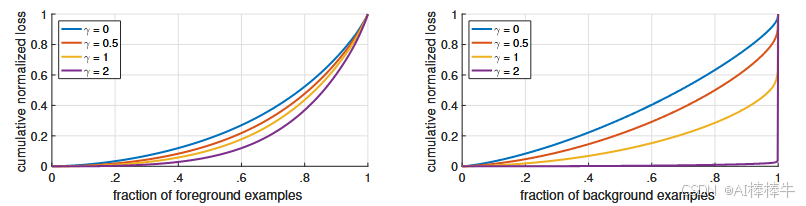
图注 :收敛模型在不同 γ \gamma γ值下,正样本和负样本的归一化损失累积分布函数。 γ \gamma γ对正样本损失分布的影响较小;但对负样本, γ \gamma γ增大时,损失会高度集中在难分样本上,几乎将所有注意力从易分负样本上转移开。
分析结论:
- 正样本 :不同 γ \gamma γ值下的损失CDF曲线差异小------约20%的难分正样本贡献了50%的正样本总损失, γ \gamma γ增大仅轻微增强这种集中性;
- 负样本 : γ \gamma γ的影响极具戏剧性------ γ = 0 \gamma=0 γ=0时,负样本与正样本的损失分布相似; γ = 2 \gamma=2 γ=2时,绝大多数负样本损失来自"极少数难分负样本",实现了对易分负样本的有效"过滤"。
5.1.5 与在线难样本挖掘(OHEM)的对比
在线难样本挖掘(OHEM)[31]的核心思想是:通过"损失得分筛选"和"NMS去重",仅保留高损失难分样本构建训练小批量;SSD[22]中还衍生出"1:3前景-背景比例约束"的OHEM变体(OHEM 1:3)。
表1d对比了焦点损失与OHEM的性能(基于ResNet-101-FPN):
- OHEM的最优性能为32.8 AP(无比例约束、批量大小128、NMS阈值0.5);
- 焦点损失的性能为36.0 AP,较OHEM最优结果高出3.2个AP,证明焦点损失在"处理密集检测类别不平衡"上更高效。
(注:我们尝试了多种OHEM参数组合,均未超过33 AP,进一步验证焦点损失的优越性。)
5.1.6 hinge损失的尝试
早期实验中,我们尝试使用"hinge损失"(对 p t p_t pt超过阈值的样本设为0损失),但训练极不稳定,未获得有效结果(详细结果见附录)。
5.2 模型架构设计分析
5.2.1 锚框密度的影响
锚框密度(每个空间位置的锚框数量)是单阶段检测器的关键设计因素(两阶段检测器可通过区域池化处理任意位置/尺度/宽高比的框)。表1c展示了"尺度数量(#sc)"和"宽高比数量(#ar)"对AP的影响(基于ResNet-50):
- 仅使用1个正方形锚框(#sc=1、#ar=1)时,AP达30.3,证明RetinaNet的基础设计有效性;
- 当使用2-3个尺度+3个宽高比时,AP提升至34.0-34.2;
- 锚框数量超过9(如#sc=4、#ar=3)时,性能饱和(AP=33.8),无进一步增益。
该结果表明:单阶段检测器通过"9个锚框/位置"即可实现与两阶段检测器相近的"目标覆盖能力",过多锚框仅增加计算量而无精度收益。
5.2.2 速度与精度的权衡(表1e、图2)
表1e展示了"骨干网络深度"和"输入图像尺度"对RetinaNet速度与精度的影响(测试于COCO test-dev):
- 骨干网络深度:相同尺度下,ResNet-101-FPN比ResNet-50-FPN的AP高1.5-2.5个百分点(如800像素尺度下,37.8 AP vs 35.7 AP),但推理时间增加约20-30毫秒;
- 输入尺度:相同骨干网络下,尺度从400像素增至800像素,AP提升5-6个百分点(如ResNet-101下,31.9 AP vs 37.8 AP),但推理时间增加1倍以上;
- 最优权衡点:ResNet-101-600(600像素尺度)的AP达36.0,推理时间122毫秒,与ResNet-101-FPN Faster R-CNN[20]的精度相当(36.2 AP),但速度快于后者(172毫秒,均基于Nvidia M40 GPU)。
图2的"速度-精度曲线"进一步验证:RetinaNet构成了当前所有检测器的"上包络线"(低精度区间除外),在相同速度下精度最高,或相同精度下速度最快。
5.3 与最先进方法的对比(表2)
表2展示了RetinaNet-101-800(800像素尺度,采用尺度抖动增强,训练时间延长1.5倍)在COCO test-dev上的性能,与现有单阶段和两阶段方法对比:
- 单阶段方法:RetinaNet的AP达39.1,较最接近的DSSD[9](33.2 AP)高出5.9个百分点,且速度更快;
- 两阶段方法:RetinaNet较基于Inception-ResNet-v2-TDM的Faster R-CNN[32](36.8 AP)高出2.3个百分点;
- 进一步优化:采用ResNeXt32x8d-101-FPN[38]作为骨干网络时,RetinaNet的AP进一步提升至40.8,突破COCO数据集40 AP大关。
表1 消融实验结果
(a) CE损失(γ=0)下α的变化对性能的影响
| α | 平均精度(AP) | IoU=0.5时AP(AP50) | IoU=0.75时AP(AP75) |
|---|---|---|---|
| 0.10 | 0.0 | 0.0 | 0.0 |
| 0.25 | 10.8 | 16.0 | 11.7 |
| 0.50 | 30.2 | 46.7 | 32.8 |
| 0.75 | 31.1 | 49.4 | 33.0 |
| 0.90 | 30.8 | 49.7 | 32.3 |
| 0.99 | 28.7 | 47.4 | 29.9 |
| 0.999 | 25.1 | 41.7 | 26.1 |
(b) FL(最优α)下γ的变化对性能的影响
| γ | α | 平均精度(AP) | IoU=0.5时AP(AP50) | IoU=0.75时AP(AP75) |
|---|---|---|---|---|
| 0 | 0.75 | 31.1 | 49.4 | 33.0 |
| 0.1 | 0.75 | 31.4 | 49.9 | 33.1 |
| 0.2 | 0.75 | 31.9 | 50.7 | 33.4 |
| 0.5 | 0.50 | 32.9 | 51.7 | 35.2 |
| 1.0 | 0.25 | 33.7 | 52.0 | 36.2 |
| 2.0 | 0.25 | 34.0 | 52.5 | 36.5 |
| 5.0 | 0.25 | 32.2 | 49.6 | 34.8 |
© 锚框尺度与宽高比数量对性能的影响
| 尺度数量(#sc) | 宽高比数量(#ar) | 平均精度(AP) | IoU=0.5时AP(AP50) | IoU=0.75时AP(AP75) |
|---|---|---|---|---|
| 1 | 1 | 30.3 | 49.0 | 31.8 |
| 2 | 1 | 31.9 | 50.0 | 34.0 |
| 3 | 1 | 31.8 | 49.4 | 33.7 |
| 1 | 3 | 32.4 | 52.3 | 33.9 |
| 2 | 3 | 34.2 | 53.1 | 36.5 |
| 3 | 3 | 34.0 | 52.5 | 36.5 |
| 4 | 3 | 33.8 | 52.1 | 36.2 |
(d) FL与OHEM基线的性能对比(ResNet-101-FPN)
| 方法 | 批量大小 | NMS阈值 | 平均精度(AP) | IoU=0.5时AP(AP50) | IoU=0.75时AP(AP75) |
|---|---|---|---|---|---|
| OHEM | 128 | 0.7 | 31.1 | 47.2 | 33.2 |
| OHEM | 256 | 0.7 | 31.8 | 48.8 | 33.9 |
| OHEM | 512 | 0.7 | 30.6 | 47.0 | 32.6 |
| OHEM | 128 | 0.5 | 32.8 | 50.3 | 35.1 |
| OHEM | 256 | 0.5 | 31.0 | 47.4 | 33.0 |
| OHEM | 512 | 0.5 | 27.6 | 42.0 | 29.2 |
| OHEM 1:3 | 128 | 0.5 | 31.1 | 47.2 | 33.2 |
| OHEM 1:3 | 256 | 0.5 | 28.3 | 42.4 | 30.3 |
| OHEM 1:3 | 512 | 0.5 | 24.0 | 35.5 | 25.8 |
| FL(本文) | - | - | 36.0 | 54.9 | 38.7 |
(e) RetinaNet的精度-速度权衡(COCO test-dev)
| 骨干网络深度 | 输入尺度(像素) | 平均精度(AP) | IoU=0.5时AP(AP50) | IoU=0.75时AP(AP75) | 小目标AP(APS) | 中目标AP(APM) | 大目标AP(APL) | 推理时间(ms) |
|---|---|---|---|---|---|---|---|---|
| ResNet-50 | 400 | 30.5 | 47.8 | 32.7 | 11.2 | 33.8 | 46.1 | 64 |
| ResNet-50 | 500 | 32.5 | 50.9 | 34.8 | 13.9 | 35.8 | 46.7 | 72 |
| ResNet-50 | 600 | 34.3 | 53.2 | 36.9 | 16.2 | 37.4 | 47.4 | 98 |
| ResNet-50 | 700 | 35.1 | 54.2 | 37.7 | 18.0 | 39.3 | 46.4 | 121 |
| ResNet-50 | 800 | 35.7 | 55.0 | 38.5 | 18.9 | 38.9 | 46.3 | 153 |
| ResNet-101 | 400 | 31.9 | 49.5 | 34.1 | 11.6 | 35.8 | 48.5 | 81 |
| ResNet-101 | 500 | 34.4 | 53.1 | 36.8 | 14.7 | 38.5 | 49.1 | 90 |
| ResNet-101 | 600 | 36.0 | 55.2 | 38.7 | 17.4 | 39.6 | 49.7 | 122 |
| ResNet-101 | 700 | 37.1 | 56.6 | 39.8 | 19.1 | 40.6 | 49.4 | 154 |
| ResNet-101 | 800 | 37.8 | 57.5 | 40.8 | 20.2 | 41.1 | 49.2 | 198 |
表2 COCO test-dev单模型目标检测结果(边界框AP)与最先进方法对比
| 方法 | 平均精度(AP) | IoU=0.5时AP(AP50) | IoU=0.75时AP(AP75) | 小目标AP(APS) | 中目标AP(APM) | 大目标AP(APL) |
|---|---|---|---|---|---|---|
| Inception-ResNet-v2 [34] | 34.7 | 55.5 | 36.7 | 13.5 | 38.1 | 52.0 |
| Inception-ResNet-v2-TDM [32] | 36.8 | 57.7 | 39.2 | 16.2 | 39.8 | 52.1 |
| DarkNet-19 [27] | 21.6 | 44.0 | 19.2 | 5.0 | 22.4 | 35.5 |
| ResNet-101-SSD [22] | 31.2 | 50.4 | 33.3 | 10.2 | 34.5 | 49.8 |
| ResNet-101-DSSD [9] | 33.2 | 53.3 | 35.2 | 13.0 | 35.4 | 51.1 |
| RetinaNet-101-FPN(本文) | 39.1 | 59.1 | 42.3 | 21.8 | 42.7 | 50.2 |
| RetinaNet-ResNeXt-101-FPN(本文) | 40.8 | 61.1 | 44.1 | 24.1 | 44.2 | 51.2 |
注:本文RetinaNet-101-800模型采用"尺度抖动"增强,训练时间为表1e中同模型的1.5倍,性能超越所有单阶段和两阶段方法。详细速度
6. 结论
本文指出,类别不平衡 是阻碍单阶段目标检测器超越最先进两阶段方法的核心障碍。为解决这一问题,我们提出焦点损失------通过在交叉熵损失中引入调制因子,将学习焦点集中在难分负样本上。该方法简洁且高效:我们设计了一款全卷积单阶段检测器(RetinaNet),并通过大量实验验证其在精度和速度上均达到最先进水平。源代码已开源至:https://github.com/facebookresearch/Detectron [12]。
附录A:焦点损失变体
焦点损失的具体形式并非唯一关键。本节将介绍一种具有相似性质的焦点损失变体(FL*),其性能与原始焦点损失(FL)相当,同时能进一步揭示焦点损失的核心特性。
A.1 焦点损失变体的定义
首先,我们将交叉熵(CE)和焦点损失(FL)改写为另一种形式,引入变量 x t x_t xt:
x t = y ⋅ x (6) x_t = y \cdot x \tag{6} xt=y⋅x(6)
其中, y ∈ { ± 1 } y \in \{±1\} y∈{±1}为真实类别(与前文一致), x x x为模型输出的logit值。此时, p t = σ ( x t ) p_t = \sigma(x_t) pt=σ(xt)( σ \sigma σ为sigmoid函数),与前文 p t p_t pt的定义兼容;当 x t > 0 x_t > 0 xt>0时,样本被正确分类( p t > 0.5 p_t > 0.5 pt>0.5)。
基于 x t x_t xt,我们定义焦点损失变体FL *,引入两个参数 γ \gamma γ(控制损失曲线陡峭度)和 β \beta β(控制损失曲线偏移量):
- 修正概率 p t ∗ p_t^* pt∗:
p t ∗ = σ ( γ ⋅ x t + β ) (7) p_t^* = \sigma(\gamma \cdot x_t + \beta) \tag{7} pt∗=σ(γ⋅xt+β)(7) - FL*损失:
F L ∗ = − log ( p t ∗ ) γ (8) FL^* = -\frac{\log(p_t^*)}{\gamma} \tag{8} FL∗=−γlog(pt∗)(8)
A.2 FL*的特性(图5)
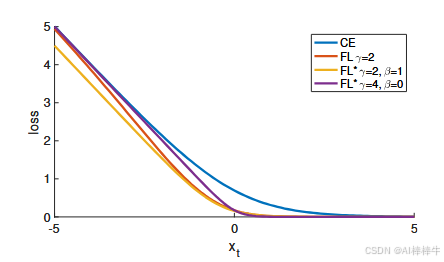
",包含CE、FL(γ=2)、FL*(γ=2, β=1)、FL*(γ=4, β=0)四条曲线)
图注 :不同损失函数随 x t = y ⋅ x x_t = y \cdot x xt=y⋅x的变化曲线。原始焦点损失(FL)与变体(FL*)均能降低"分类良好样本( x t > 0 x_t > 0 xt>0)"的相对损失。
如图5所示,FL*与原始FL具有相似特性:通过 γ \gamma γ和 β \beta β的调节,能有效降低易分样本( x t > 0 x_t > 0 xt>0)的损失权重,同时保留难分样本的损失信号。
A.3 FL*的性能验证(表3)
我们在RetinaNet-50-600模型上进行实验,使用与原始FL完全相同的训练设置,仅将损失函数替换为FL*,结果如表3所示:
| 损失函数 | γ | β | 平均精度(AP) | IoU=0.5时AP(AP50) | IoU=0.75时AP(AP75) |
|---|---|---|---|---|---|
| CE | --- | --- | 31.1 | 49.4 | 33.0 |
| FL(原文) | 2.0 | --- | 34.0 | 52.5 | 36.5 |
| FL* | 2.0 | 1.0 | 33.8 | 52.7 | 36.3 |
| FL* | 4.0 | 0.0 | 33.9 | 51.8 | 36.4 |
表3 FL与FL*及CE的性能对比(选定参数)
实验表明,FL的AP(33.8-33.9)与原始FL(34.0)几乎持平,证明FL 是原始FL的有效替代方案。进一步实验(图7)显示,多种 γ \gamma γ和 β \beta β组合均能实现AP>33.5的有效性能(图中蓝色曲线标注),核心要求是"损失函数需降低分类良好样本( x t > 0 x_t > 0 xt>0)的权重"。
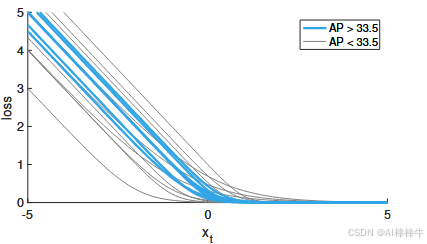
图7 FL*不同参数设置的有效性
",曲线按"AP>33.5(蓝色)"和"AP<33.5(非蓝色)"分类,展示不同 γ \gamma γ和 β \beta β下的FL 曲线)
图注 :FL*在不同 γ \gamma γ和 β \beta β设置下的有效性。曲线颜色标注:有效设置(模型收敛且AP>33.5)为蓝色,无效设置为其他颜色。实验中为简化操作,统一使用 α = 0.25 \alpha=0.25 α=0.25。可见,能降低"分类良好样本( x t > 0 x_t > 0 xt>0)"权重的损失函数均能实现有效性能。
A.4 通用结论
任何具有"降低易分样本损失权重、聚焦难分样本"特性的损失函数,均有望在密集目标检测中实现与FL/FL*相当的效果。
附录B:损失函数的导数
为方便参考,本节给出CE、FL、FL*三种损失函数对 x x x的导数( x x x为模型输出的logit值):
-
交叉熵(CE)的导数:
d C E d x = y ⋅ ( p t − 1 ) \frac{d\ CE}{d\ x} = y \cdot (p_t - 1) d xd CE=y⋅(pt−1) -
焦点损失(FL)的导数:
d F L d x = y ⋅ ( 1 − p t ) γ ⋅ ( γ ⋅ p t ⋅ log ( p t ) + p t − 1 ) \frac{d\ FL}{d\ x} = y \cdot (1-p_t)^\gamma \cdot (\gamma \cdot p_t \cdot \log(p_t) + p_t - 1) d xd FL=y⋅(1−pt)γ⋅(γ⋅pt⋅log(pt)+pt−1) -
焦点损失变体(FL*)的导数:
d F L ∗ d x = y ⋅ ( p t ∗ − 1 ) \frac{d\ FL^*}{d\ x} = y \cdot (p_t^* - 1) d xd FL∗=y⋅(pt∗−1)
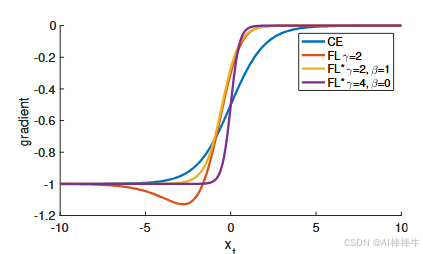
导数特性(图6)
",包含CE、FL(γ=2)、FL*(γ=2, β=1)、FL*(γ=4, β=0)四条导数曲线)
图注 :图5中各损失函数对 x x x的导数曲线。所有损失函数在"高置信度预测"时导数趋近于-1或0;但与CE不同,FL和FL*的有效设置在 x t > 0 x_t > 0 xt>0(正确分类)时,导数迅速减小,避免易分样本主导梯度更新。
参考文献
略