Slotted Aloha - 技术栈

1.论文主要思路

论文地址：Stability and Delay Analysis of Buffered Aloha Networks

一、核心仿真模型与假设

论文的仿真模型是构建其理论分析的基础，其核心是一个离散时间的、基于时隙的仿真系统。

网络拓扑与节点 ：
- 仿真一个包含 n 个节点的网络。
- 所有节点是同构的，具有相同的参数和行为。
流量模型 ：
- 每个节点都有一个无限大小的缓冲区。
- 数据包以 伯努利过程 到达每个节点，到达率为 λ。
- 这意味着在每个时隙开始时，一个节点独立地以概率 λ 产生一个新包。
队列服务规则 ：
- 先进先出。
- 只有队首包 有资格参与信道竞争。这是"Buffered Aloha"与经典无缓冲区Aloha的关键区别。
信道访问机制 ：
- 时间被划分为时隙，传输在每个时隙开始时进行。
- 一个HOL包能否传输，取决于它当前的相位和退避因子 q。
- 采用 K-指数退避 框架：
  - 一个新成为HOL的包处于相位 0 ，传输概率为 ( q 0 = 1 ) ( q^0 = 1 ) (q0=1)。
  - 如果传输发生碰撞，则进入下一相位（相位 1），传输概率变为 ( q 1 ) ( q^1 ) (q1)。
  - 以此类推，直到达到截止相位 K 。相位 K 的包以概率 ( q K ) ( q^K ) (qK) 传输。
  - 几何重传 是 ( K=1 ) 的特例：所有重传包都以概率 ( q ) 传输。
  - 指数退避 是 ( K=\infty ) 的特例：包可以无限后退，传输概率不断降低。
碰撞模型 ：
- 理想化的：如果在同一个时隙内有超过一个节点传输，则发生碰撞，所有传输的包都失败。
- 碰撞的包会根据上述规则进入更高的相位（重传状态）。

二、主要仿真指标

论文中明确或隐含地追踪了以下关键性能指标，这些是验证其理论的核心：

瞬态成功概率 ( p t ) ( p_t ) (pt)：
- 定义：到第 ( t ) 个时隙为止，所有HOL包传输尝试中，成功传输的比例。
- 计算方式 ： ( p t = 到时隙t为止累计的成功传输次数到时隙t为止累计的传输尝试次数 ) ( p_t = \frac{\text{到时隙t为止累计的成功传输次数}}{\text{到时隙t为止累计的传输尝试次数}} ) (pt=到时隙t为止累计的传输尝试次数到时隙t为止累计的成功传输次数)
- 目的：这是最重要的观测变量 。用于直接观察系统动态：
  - 收敛到期望稳定点 ( p L ) ( p_L ) (pL)（高吞吐量，稳定）。
  - 还是收敛到非期望稳定点 ( p A ) ( p_A ) (pA)（低吞吐量，饱和状态）。
  - 验证理论分析中预测的双稳态特性。
网络吞吐量 ( λ ^ o u t ) ( \hat{\lambda}_{out} ) (λ^out)：
- 定义：长期来看，整个网络平均每时隙成功传输的包数量。
- 计算方式 ：在足够长的仿真时间 ( T ) 内， ( λ ^ o u t = 总成功传输包数 T ) ( \hat{\lambda}_{out} = \frac{\text{总成功传输包数}}{T} ) (λ^out=T总成功传输包数)。
- 目的：验证稳定性 。论文定义"稳定"为 ( λ ^ o u t = λ ^ = n λ ) ( \hat{\lambda}_{out} = \hat{\lambda} = n\lambda ) (λ^out=λ^=nλ)。如果吞吐量低于输入率，说明系统不稳定，队列会无限增长。
访问延迟：
- 定义：一个包从它成为HOL包的时刻开始，到它被成功传输出去的时刻为止，所经历的时隙数。
- 观测的统计量 ：
  - 一阶矩 ( E [ D 0 ] ) ( E[D_0] ) (E[D0])：平均访问延迟。
  - 二阶矩 ( E [ D 0 2 ] ) ( E[D_0^2] ) (E[D02]) ：访问延迟的方差，用于衡量延迟抖动。
- 目的：
  - 比较不同退避参数下的延迟性能。
  - 验证理论公式（如公式60, 61）的正确性。
  - 揭示指数退避在非期望稳定点 ( p A ) ( p_A ) (pA) 下的"捕获现象"，表现为二阶矩急剧增大甚至发散（无穷大）。
系统状态收敛性：
- 这是一个定性但至关重要的指标。仿真通过观察 ( p t ) ( p_t ) (pt) 随时间 ( t ) 的变化轨迹，来判断系统最终收敛于哪个稳定点。这直接对应理论分析中的动态方程。

三、仿真运行逻辑与参数扫描

论文的仿真并非只运行一种参数设置，而是进行了系统的参数扫描，以绘制出完整的性能图景：

验证双稳态：
- 固定 ( n ), ( λ ^ ) ( \hat{\lambda} ) (λ^), ( K )。
- 选择不同的退避因子 ( q ) ，特别是选择在绝对稳定区域 ( S L ) ( S_L ) (SL) 内和外的值。
- 对每个 ( q )，运行仿真，观察 ( p_t ) 的轨迹，看它是收敛到 ( p L ) ( p_L ) (pL) 还是 ( p A ) ( p_A ) (pA)。（对应 图10）
绘制稳定区域：
- 固定 ( n ), ( λ ^ ) ( \hat{\lambda} ) (λ^), ( K )。
- 扫描不同的 ( q ) 值，对于每个 ( q )，测量稳态下的吞吐量 ( λ ^ o u t ) ( \hat{\lambda}_{out} ) (λ^out)。
- 将满足 ( λ ^ o u t = λ ^ ) ( \hat{\lambda}_{out} = \hat{\lambda} ) (λ^out=λ^) 的 ( q ) 范围标记为稳定区域。（对应 图11, 12, 13）
分析延迟性能：
- 在稳定区域内，对于每个 ( q )，测量并记录 ( E [ D 0 ] ) ( E[D_0] ) (E[D0]) 和 ( E [ D 0 2 ] ) ( E[D_0^2]) (E[D02])。
- 找到使延迟最小化的最优 ( q ) ，并与理论公式（如66）进行对比。（对应 图14）
研究截止相位 ( K ) 的影响：
- 固定 ( n ), ( λ ^ ) ( \hat{\lambda} ) (λ^), ( q )。
- 变化 ( K ) 的值（如 1, 2, 4, 8, 16, ∞）。
- 对每个 ( K )，测量吞吐量和延迟的二阶矩，展示 ( K ) 在稳定性 和延迟抖动 之间的权衡。（对应 图15）

思考：可以明显看出，虽然本文提到了slotted Aloha，但其实本质上本文提到的是一个加了K退避优化的slotted Aloha变种，所以我们先做基础的slotted Aloha的简单仿真，之后再考虑进行K退避优化

2.我的仿真代码思路（以吞吐量仿真为例）

实现一个基础的、带有固定传输概率的时隙ALOHA协议 仿真，核心目标是扫描不同传输概率 q，并测量对应的系统吞吐量和信令开销。

一、核心模型与假设

网络模型：
- 节点数量 ：node_sum 个同构节点。
- 流量模型 ：每个节点在每个时隙有独立且相同的概率 lambda 产生一个新包。这是一个伯努利到达过程 ，总到达率为 Lambda_total = node_sum * lambda。
- 队列模型 ：每个节点维护一个队列（代码中用 Node_state_current(:, 2) 表示队列长度）。这是一个缓冲式ALOHA 模型。
协议机制：
- 时隙化：时间被划分为等长的时隙，所有传输在时隙开始时同步进行。
- 传输决策 ：
  - 只有队列非空的节点才可能传输。
  - 每个这样的节点，独立地以固定概率 q 决定在本时隙是否传输。
  - 这与论文中的 几何重传（K=1） 模型完全一致。节点不记忆碰撞历史，每次传输尝试的概率都是 q。
碰撞与成功：
- 如果一个时隙内有且仅有一个节点传输，则传输成功。
- 如果传输节点数为0（空闲）或大于1（碰撞），则该时隙没有成功传输。

二、仿真流程与逻辑（逐时隙）

仿真核心是一个嵌套循环：外层循环遍历不同的 q 值，内层循环对每个 q 进行 Total_slot 个时隙的模拟。

对于每个时隙 t，执行以下步骤：

包到达（向量化）：
- 为所有节点生成随机数，判断本时隙是否有新包到达。
- 将到达的包加入对应节点的队列。Node_state_current(:, 2) = Node_state_current(:, 2) + arrivals;
传输决策（向量化）：
- 找出所有队列非空的节点。has_packet = Node_state_current(:, 2) > 0;
- 在这些节点中，根据概率 q 决定哪些节点在本时隙尝试传输。should_transmit = has_packet & attempt_prob;
- 记录尝试传输的节点数 num_attempt_this_slot。
冲突检测与成功处理：
- 如果 num_attempt_this_slot == 1，则视为成功传输。
  - 总成功次数 Total_success 加1。
  - 成功节点的队列长度减1。Node_state_current(node_transmit, 2) = max(0, ...) - 1);
状态重置与指标记录：
- 信令开销 ：将本时隙的尝试次数累加到 signaling_count。这反映了系统的冲突水平和控制开销。
- 重置所有节点的"发送标志位"，为下一个时隙做准备。Node_state_current(:, 1) = 0;

三、关键性能指标

吞吐量 throughputD_simu：
- 定义：平均每个时隙成功传输的包数量。
- 计算：Total_success / Total_slot。
- 目的：这是最核心的性能指标 ，用于绘制经典的"吞吐量 vs. 提供负载（或传输概率 q）"曲线，找到使吞吐量最大化的最优 q。
信令开销 ST：
- 定义：平均每个时隙发生的传输尝试次数（包括成功的和冲突的）。
- 计算：signaling_count / Total_slot。
- 目的：衡量信道竞争的激烈程度和协议效率。过高的 ST 意味着大量能量和资源浪费在冲突上。

四、仿真策略与特点

参数扫描：
- 通过外层循环遍历 ACB_bw 数组（即不同的 q 值），系统地研究传输概率对系统性能的影响。
性能评估：
- 仿真的最终目标是得到两条曲线：
  - throughputD_simu 随 q 变化的曲线。
  - ST 随 q 变化的曲线。
- 通过分析这些曲线，可以确定系统的最佳工作点。
优化技巧：
- 使用了向量化操作，对所有节点的到达和传输决策进行批量随机数生成和逻辑判断，大大提升了仿真效率。
- 预生成随机数矩阵（arrival_rand, transmit_rand）是可选的优化，有助于减少循环内的计算开销。

与论文仿真思路的对比

方面	我的仿真思路	论文中的仿真思路
核心协议	几何重传 (K=1) ，固定传输概率 `q`	K-指数退避框架，传输概率随碰撞次数变化
关键观测变量	无	瞬态成功概率 ( p t ) ( p_t ) (pt)
性能指标	吞吐量、信令开销 (ST)	吞吐量、平均延迟、延迟二阶矩
分析重点	寻找最优固定 `q`，以最大化吞吐量	分析双稳态、稳定区域、延迟抖动与 `K` 的关系
节点状态	队列长度	队列长度 + 相位 (0 to K)
动态行为	无记忆性，每次尝试概率相同	有记忆性，碰撞后退避，传输概率降低

结论

我的仿真代码实现了一个经典且基础的缓冲式时隙ALOHA模型 ，旨在通过蒙特卡洛仿真验证ALOHA协议的基本特性：

在轻负载下，低 q 可能导致信道利用率不足。
在重负载下，高 q 会导致过多冲突，吞吐量下降。
存在一个最优的 q，使得吞吐量达到最大值。

与论文相比，我的仿真更侧重于协议的"静态"性能评估（扫描q），而论文则深入研究了协议的"动态"行为（收敛性、稳定性）和更复杂的退避机制（K>1）及其对延迟的影响。如果再进一步研究，可以考虑引入相位（碰撞计数） 和K-指数退避机制 ，并追踪瞬态成功概率 ( p_t ) 和包延迟的高阶矩。

3.主要仿真思路、结果与分析

吞吐量

跳转到2看吞吐量

代码Main4：

matlab 复制代码

clc;clear;close all;
%% 吞吐量仿真比较：GF vs SAST vs 时隙ALOHA

ACB_bw_simu = [0.0001,0.001:0.001:0.01];
Lambda_total = 1; % 饱和情况
Node_num = 100;
Total_slot = 2e6;
Node_state = zeros(100,2);

% 运行三种协议的仿真
[throughputD_simu1, pt_simu1, ST1] = GF_1(Node_state, ACB_bw_simu, Lambda_total, Total_slot);
[throughputD_simu3, throughputA_simu3, pt_simu3, ST3] = SAST_1(Node_state, ACB_bw_simu, Lambda_total, Total_slot);
[throughputD_simu4, ST4] = slotted_ALOHA(Node_state, ACB_bw_simu, Lambda_total, Total_slot);

%% 理论吞吐量分析
ACB_bw_ana = linspace(0, 0.01, 100);
n = Node_num;

% GF协议理论吞吐量
throughput1_ana = n .* ACB_bw_ana .* exp(-n .* ACB_bw_ana);

% SAST协议理论吞吐量  
nq = n .* ACB_bw_ana;
throughput3_ana = nq ./ (exp(nq) + nq - 1);

% 时隙ALOHA理论吞吐量
throughput4_ana = n .* ACB_bw_ana .* exp(-n .* ACB_bw_ana);

%% 画图 - 吞吐量比较
figure 
hold on;

% 颜色配置
figcol = cell(1,3);
figcol{1} = '#336633';  % GF - 绿色
figcol{2} = '#5C0DAC';  % SAST - 紫色  
figcol{3} = '#FF0000';  % 时隙ALOHA - 红色

% 标记形状配置
figshape = cell(1,3);
figshape{1} = '*';
figshape{2} = 'O';
figshape{3} = 'square';

linewidth = 1;
markersize = 60;

% GF协议
i = 1;
f1 = plot(ACB_bw_ana, throughput1_ana, '-', 'color', figcol{i}, 'LineWidth', linewidth);
s1 = scatter(ACB_bw_simu, throughputD_simu1, markersize, 'MarkerEdgeColor', figcol{i}, ...
    'Marker', figshape{i}, 'LineWidth', linewidth);

% SAST协议
i = 2;
f2 = plot(ACB_bw_ana, throughput3_ana, '--', 'color', figcol{i}, 'LineWidth', linewidth);
s2 = scatter(ACB_bw_simu, throughputD_simu3, markersize, 'MarkerEdgeColor', figcol{i}, ...
    'Marker', figshape{i}, 'LineWidth', linewidth);

% 时隙ALOHA协议
i = 3;
f3 = plot(ACB_bw_ana, throughput4_ana, ':', 'color', figcol{i}, 'LineWidth', linewidth);
s3 = scatter(ACB_bw_simu, throughputD_simu4, markersize, 'MarkerEdgeColor', figcol{i}, ...
    'Marker', figshape{i}, 'LineWidth', linewidth);

hold off;
xlim([0, max(ACB_bw_ana)]);
% 修正字体设置 - 统一使用英文或统一字体
xlabel('Transmission Probability', 'FontName', 'Times New Roman', 'fontsize', 14);
ylabel('Throughput', 'FontName', 'Times New Roman', ...
    'rotation', 0, 'Horizontalalignment', 'right', 'fontsize', 14);

% 或者如果您需要中文标签，可以这样设置：
% xlabel('传输概率', 'FontName', 'SimSun', 'fontsize', 14);
% ylabel('吞吐量', 'FontName', 'SimSun', ...
%     'rotation', 0, 'Horizontalalignment', 'right', 'fontsize', 14);

legend([f1, s1, f2, s2, f3, s3], ...
    {'GF Analysis', 'GF Simulation', 'SAST Analysis', 'SAST Simulation', ...
     'Slotted ALOHA Analysis', 'Slotted ALOHA Simulation'}, ...
    'FontName', 'Times New Roman'); % 确保图例也使用相同字体

set(gca, 'position', [0.15, 0.15, 0.7, 0.7], 'LineWidth', 0.5, 'fontsize', 14, 'FontName', 'Times New Roman');
set(gcf, 'unit', 'normalized', 'position', [.2, .2, 0.4, 0.45]);
grid on;
box on;

save('throughput_comparison.mat');

slotted_ALOHA.m

matlab 复制代码

function [throughputD_simu, ST] = slotted_ALOHA(Node_state, ACB_bw, Lambda_total, Total_slot)
% 时隙ALOHA协议仿真（向量化高速版）

    [node_sum, ~] = size(Node_state);
    num_q = max(size(ACB_bw));
    
    throughputD_simu = zeros(1, num_q);
    ST = zeros(1, num_q);

    lambda_hat = Lambda_total;
    lambda = lambda_hat / node_sum;  % 每个节点的到达率

    for k = 1:num_q
        q = ACB_bw(k);
        
        Total_success = 0;
        signaling_count = 0;
        
        % 初始化节点状态: [是否发送, 队列长度]
        Node_state_current = zeros(node_sum, 2);
        
        % 预生成所有时隙所需的随机数（可选，节省时间）
        % 如果内存允许，可以一次性生成
        arrival_rand = rand(Total_slot, node_sum);      % 包到达用
        transmit_rand = rand(Total_slot, node_sum);     % 发送决策用
        
        for t = 1:Total_slot
            % Step 1: 包到达（向量化）
            arrivals = arrival_rand(t, :)' < lambda;
            Node_state_current(:, 2) = Node_state_current(:, 2) + arrivals;
            
            % Step 2: 传输决策（向量化）
            has_packet = Node_state_current(:, 2) > 0;
            attempt_prob = transmit_rand(t, :)' < q;
            should_transmit = has_packet & attempt_prob;
            
            Node_state_current(should_transmit, 1) = 1;
            num_attempt_this_slot = sum(should_transmit);
            
            % Step 3: 冲突检测
            if num_attempt_this_slot == 1
                % 成功
                node_transmit = find(should_transmit, 1);
                Total_success = Total_success + 1;
                Node_state_current(node_transmit, 2) = max(0, Node_state_current(node_transmit, 2) - 1);
            else
                node_transmit = 0;  % 冲突或无传输
            end
            
            % Step 4: 信令开销和状态重置
            signaling_count = signaling_count + num_attempt_this_slot;
            Node_state_current(:, 1) = 0;  % 所有节点重置发送标志
        end
        
        % 记录结果
        throughputD_simu(k) = Total_success / Total_slot;
        ST(k) = signaling_count / Total_slot;
    end
end

结果：

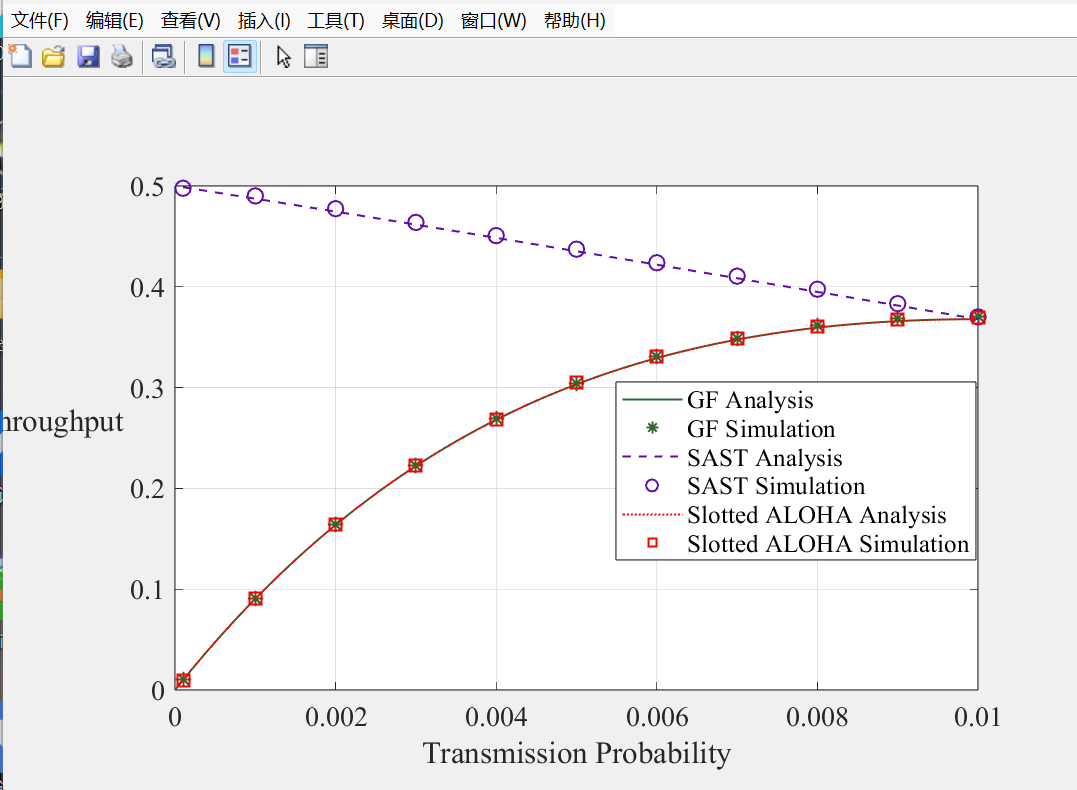
分析：slottedAloha的吞吐量与给的模板GF差不多，所以可以认为仿真效果很好

STR

主要思路是比较三种随机接入协议在饱和情况下的信令开销性能。以下是详细分析：

核心目标

比较GF、SAST和时隙ALOHA三种协议的信令传输比(STR)，即每成功传输一个数据包所需的信令开销。

代码结构分析

1. 参数设置

matlab 复制代码

ACB_bw_simu = [0.0001,0.001:0.001:0.01];  % 接入概率范围
Lambda_total = 1;    % 总到达率
Node_num = 100;      % 节点数量
Total_slot = 2e6;    % 总时隙数

2. 仿真执行

调用三个协议的仿真函数：

GF协议 ：GF_1() - 获取吞吐量和信令传输量
SAST协议 ：SAST_1() - 获取吞吐量和信令传输量
时隙ALOHA ：slotted_ALOHA() - 获取吞吐量和信令传输量

3. 性能指标计算

计算信令传输比(STR)：

matlab 复制代码

STR = 信令传输量 / 成功传输的数据包数

这个指标反映了协议的效率，值越小说明信令开销越小。

4. 理论分析

为每个协议建立理论模型：

GF协议 ：STR1_ana = 2*exp(Node_num.*ACB_bw_ana)
SAST协议 ：STR3_ana = 2*exp(nq)+2*nq-exp(-nq)
时隙ALOHA ：STR4_ana = 2./(Node_num.*ACB_bw_ana.*exp(-Node_num.*ACB_bw_ana))

5. 可视化比较

绘制理论曲线和仿真散点图：

使用不同颜色和标记区分三种协议
理论分析用连续线型，仿真结果用散点标记
设置专业的数据可视化格式

关键特点

饱和场景：假设系统处于高负载状态
双验证：同时进行理论分析和仿真验证
完整对比：从极低概率(0.0001)到较高概率(0.01)全面比较
标准化指标：使用STR作为统一的比较标准

预期输出

通过图形展示三种协议在不同接入概率下的信令开销性能，验证理论模型的准确性，并为协议选择提供依据。

代码：

matlab 复制代码

clc;clear;close all;
%% 比较三种协议的信令开销（饱和情况下） :仿真 1：GF 3：SAST 4：时隙ALOHA

ACB_bw_simu=[0.0001,0.001:0.001:0.01];%这里与demo不同，只有20个数据点不够，所以采用这种分类方式，
%极低概率：0.0001（非常保守）
%低概率：0.001-0.005（适度竞争）
%中等概率：0.006-0.01（相对积极）
Lambda_total=1;%总包到达率
Node_num=100;
Total_slot=2e6;
Node_state=zeros(100,2);

% 运行三种协议的仿真
[throughputD_simu1,pt_simu1,ST1] = GF_1(Node_state,ACB_bw_simu,Lambda_total,Total_slot);
[throughputD_simu3,throughputA_simu3,pt_simu3,ST3] = SAST_1(Node_state,ACB_bw_simu,Lambda_total,Total_slot);
[throughputD_simu4,ST4] = slotted_ALOHA(Node_state,ACB_bw_simu,Lambda_total,Total_slot);

% 计算信令传输比
STR1_simu=ST1./throughputD_simu1;
STR3_simu=ST3./throughputD_simu3;
STR4_simu=ST4./throughputD_simu4;

%% 理论分析
ACB_bw_ana=linspace(0,0.01,100);

% 原有理论公式
STR1_ana=2*exp(Node_num.*ACB_bw_ana);
nq=Node_num.*ACB_bw_ana;
STR3_ana=2*exp(nq)+2*nq-exp(-nq);

% 时隙ALOHA理论公式
STR4_ana = 2 ./ (Node_num .* ACB_bw_ana .* exp(-Node_num .* ACB_bw_ana));

save('Main1_saterated_STR');

%% 画图 - 饱和的信令开销（包含时隙ALOHA）
figure 
hold on;

% 颜色配置
figcol=cell(1,4);
figcol{1}='#336633';  % GF - 绿色
figcol{2}='#5C0DAC';  % SAST - 紫色
figcol{3}='#FF0000';  % 时隙ALOHA - 红色

% 标记形状配置
figshape=cell(1,4);
figshape{1}='*';
figshape{2}='O';
figshape{3}='square';
figshape{4}='diamond';

linewidth=1;
markersize=60;

% GF协议
i=1;
f1=plot(ACB_bw_ana,STR1_ana,'-','color',figcol{i},'LineWidth',linewidth);
s1=scatter(ACB_bw_simu,STR1_simu,markersize,'MarkerEdgeColor',figcol{i},...
    'Marker',figshape{i},'LineWidth',linewidth);

% SAST协议
i=2;
f2=plot(ACB_bw_ana,STR3_ana,'--','color',figcol{i},'LineWidth',linewidth);
s2=scatter(ACB_bw_simu,STR3_simu,markersize,'MarkerEdgeColor',figcol{i},...
    'Marker',figshape{i},'LineWidth',linewidth);

% 时隙ALOHA协议
i=3;
f3=plot(ACB_bw_ana,STR4_ana,':','color',figcol{i},'LineWidth',linewidth);
s3=scatter(ACB_bw_simu,STR4_simu,markersize,'MarkerEdgeColor',figcol{i},...
    'Marker',figshape{i},'LineWidth',linewidth);

hold off;
xlim([0,max(ACB_bw_ana)]);
xlabel('$q$','Interpreter','latex');
ylabel('STR','Interpreter','tex','rotation',0,'Horizontalalignment','right');
legend([f1,s1,f2,s2,f3,s3],{'GF Analysis','GF Simulation','SAST Analysis','SAST Simulation',...
    'Slotted ALOHA Analysis','Slotted ALOHA Simulation'});
set (gca,'position',[0.15,0.15,0.7,0.7],'LineWidth',0.5,'fontsize',14,'FontName','Times New Roman');
set(gcf,'unit','normalized','position', [.2,.2,0.4,0.45]);
box on

结果：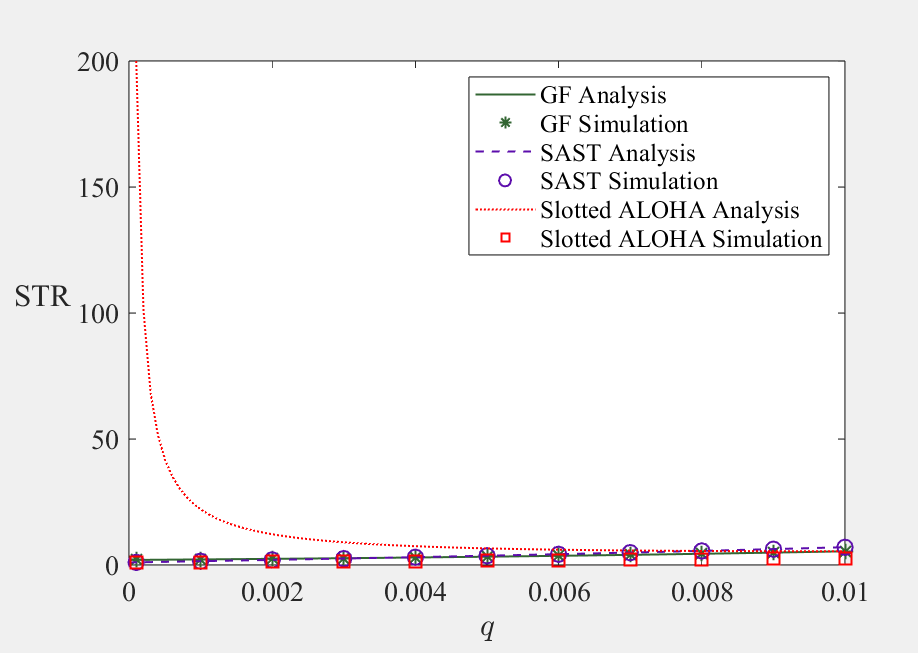

分析：这个显示效果不好，换一个更好的

matlab 复制代码

clc; clear; close all;
%% 比较三种协议的信令开销（饱和情况下） :仿真 1：GF 3：SAST 4：时隙ALOHA

ACB_bw_simu = [0.0001, 0.001:0.001:0.01];
Lambda_total = 1; % 总包到达率
Node_num = 100;
Total_slot = 2e6;
Node_state = zeros(100, 2);

% 运行三种协议的仿真
[throughputD_simu1, pt_simu1, ST1] = GF_1(Node_state, ACB_bw_simu, Lambda_total, Total_slot);
[throughputD_simu3, throughputA_simu3, pt_simu3, ST3] = SAST_1(Node_state, ACB_bw_simu, Lambda_total, Total_slot);
[throughputD_simu4, ST4] = slotted_ALOHA(Node_state, ACB_bw_simu, Lambda_total, Total_slot);

% 计算信令传输比
STR1_simu = ST1 ./ throughputD_simu1;
STR3_simu = ST3 ./ throughputD_simu3;
STR4_simu = ST4 ./ throughputD_simu4;

%% 理论分析
ACB_bw_ana = linspace(0.0001, 0.01, 100); % 避免除零错误

% 原有理论公式
STR1_ana = 2 * exp(Node_num .* ACB_bw_ana);
nq = Node_num .* ACB_bw_ana;
STR3_ana = 2 * exp(nq) + 2 * nq - exp(-nq);

% 时隙ALOHA理论公式 - 避免除零错误
STR4_ana = 2 ./ (Node_num .* ACB_bw_ana .* exp(-Node_num .* ACB_bw_ana));

save('Main1_saterated_STR.mat');

%% 画图 - 饱和的信令开销（包含时隙ALOHA）
figure('Units', 'normalized', 'Position', [0.1, 0.1, 0.7, 0.6]);
hold on;

% 颜色配置
figcol = cell(1, 3);
figcol{1} = '#336633';  % GF - 绿色
figcol{2} = '#5C0DAC';  % SAST - 紫色  
figcol{3} = '#FF0000';  % 时隙ALOHA - 红色

% 标记形状配置
figshape = cell(1, 3);
figshape{1} = '*';
figshape{2} = 'o';
figshape{3} = 'square';

linewidth = 2;
markersize = 8;

% GF协议
i = 1;
f1 = plot(ACB_bw_ana, STR1_ana, '-', 'Color', figcol{i}, 'LineWidth', linewidth);
s1 = scatter(ACB_bw_simu, STR1_simu, markersize*3, 'MarkerEdgeColor', figcol{i}, ...
    'Marker', figshape{i}, 'LineWidth', linewidth, 'MarkerFaceColor', figcol{i});

% SAST协议
i = 2;
f2 = plot(ACB_bw_ana, STR3_ana, '--', 'Color', figcol{i}, 'LineWidth', linewidth);
s2 = scatter(ACB_bw_simu, STR3_simu, markersize*3, 'MarkerEdgeColor', figcol{i}, ...
    'Marker', figshape{i}, 'LineWidth', linewidth, 'MarkerFaceColor', figcol{i});

% 时隙ALOHA协议
i = 3;
f3 = plot(ACB_bw_ana, STR4_ana, ':', 'Color', figcol{i}, 'LineWidth', linewidth);
s3 = scatter(ACB_bw_simu, STR4_simu, markersize*3, 'MarkerEdgeColor', figcol{i}, ...
    'Marker', figshape{i}, 'LineWidth', linewidth, 'MarkerFaceColor', figcol{i});

hold off;

% 修正坐标轴和标签设置
xlim([0, max(ACB_bw_ana)]);
% 设置y轴范围，避免无穷大值
ylim([0, min(100, max([STR1_simu, STR3_simu, STR4_simu]) * 1.1)]);

% 修正标签设置 - 移除LaTeX解释器
xlabel('传输概率 q', 'FontSize', 12, 'FontWeight', 'bold');
ylabel('STR', 'FontSize', 12, 'FontWeight', 'bold', 'Rotation', 0, 'HorizontalAlignment', 'right');

% 修正图例设置
legend([f1, f2, f3], {'GF理论', 'SAST理论', '时隙ALOHA理论'}, ...
    'Location', 'best', 'FontSize', 10);

% 或者如果想要显示仿真点，可以使用：
% legend([f1, s1, f2, s2, f3, s3], ...
%     {'GF理论', 'GF仿真', 'SAST理论', 'SAST仿真', '时隙ALOHA理论', '时隙ALOHA仿真'}, ...
%     'Location', 'best', 'FontSize', 9, 'NumColumns', 2);

% 修正坐标轴设置
ax = gca;
ax.FontSize = 11;
ax.LineWidth = 1;
ax.Box = 'on';
grid on;

% 可选：添加标题
title('协议信令开销比较', 'FontSize', 14, 'FontWeight', 'bold');

% 保存图形
saveas(gcf, 'STR_comparison.png');

%% 如果时隙ALOHA的值太大，可以考虑使用对数坐标
% 创建一个对数坐标的图形来更好显示数据
figure('Units', 'normalized', 'Position', [0.1, 0.1, 0.7, 0.6]);
semilogy(ACB_bw_ana, STR1_ana, '-', 'Color', figcol{1}, 'LineWidth', linewidth);
hold on;
semilogy(ACB_bw_ana, STR3_ana, '--', 'Color', figcol{2}, 'LineWidth', linewidth);
semilogy(ACB_bw_ana, STR4_ana, ':', 'Color', figcol{3}, 'LineWidth', linewidth);

scatter(ACB_bw_simu, STR1_simu, markersize*3, 'MarkerEdgeColor', figcol{1}, ...
    'Marker', figshape{1}, 'LineWidth', linewidth, 'MarkerFaceColor', figcol{1});
scatter(ACB_bw_simu, STR3_simu, markersize*3, 'MarkerEdgeColor', figcol{2}, ...
    'Marker', figshape{2}, 'LineWidth', linewidth, 'MarkerFaceColor', figcol{2});
scatter(ACB_bw_simu, STR4_simu, markersize*3, 'MarkerEdgeColor', figcol{3}, ...
    'Marker', figshape{3}, 'LineWidth', linewidth, 'MarkerFaceColor', figcol{3});
hold off;

xlabel('传输概率 q', 'FontSize', 12, 'FontWeight', 'bold');
ylabel('STR (对数坐标)', 'FontSize', 12, 'FontWeight', 'bold', 'Rotation', 90);
legend('GF理论', 'SAST理论', '时隙ALOHA理论', 'GF仿真', 'SAST仿真', '时隙ALOHA仿真', ...
    'Location', 'best', 'FontSize', 9);
grid on;
title('协议信令开销比较（对数坐标）', 'FontSize', 14, 'FontWeight', 'bold');
saveas(gcf, 'STR_comparison_log.png');

保存在Slotted Aloha.fig

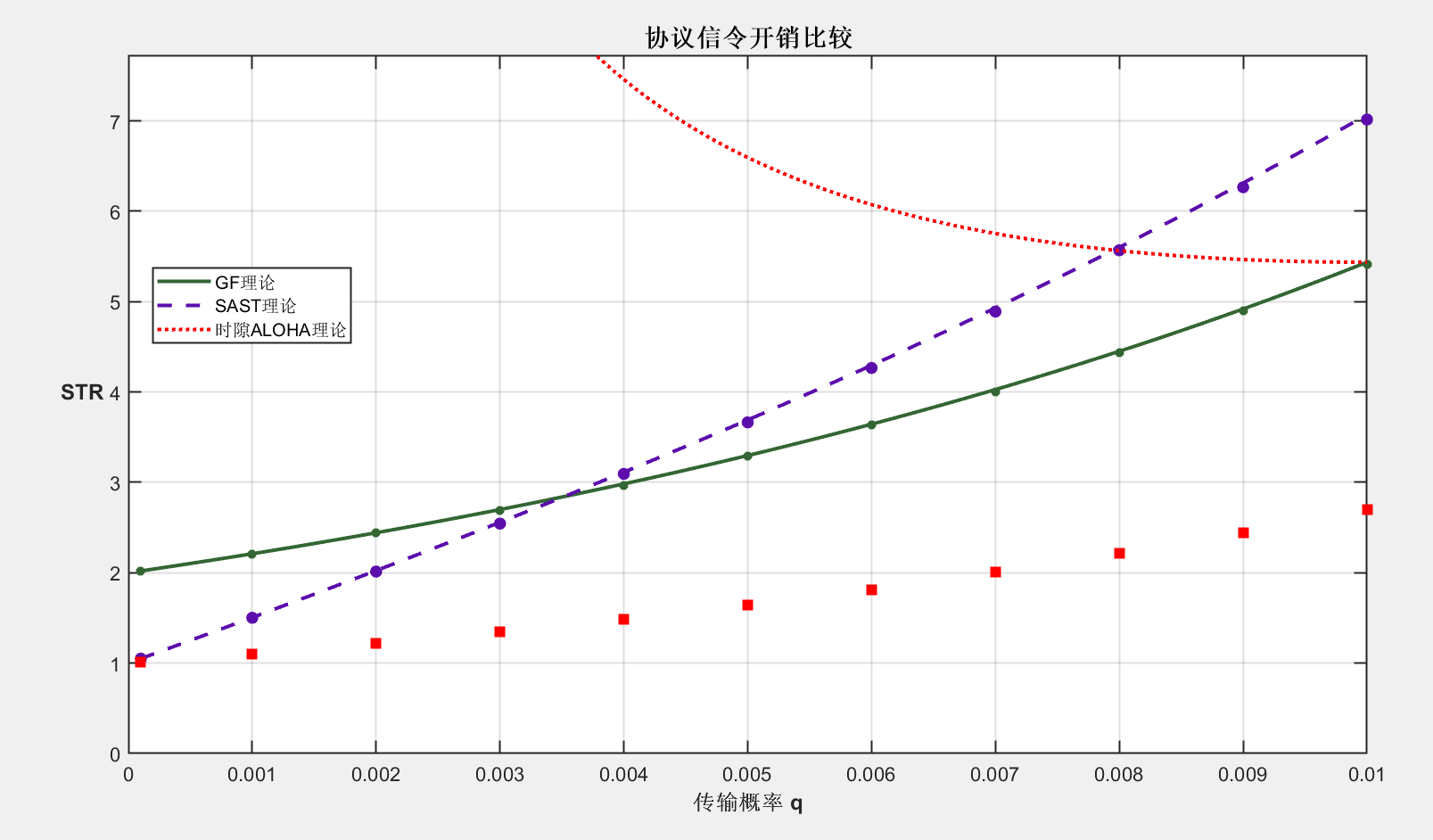
保存在slotted STR10.25.fig

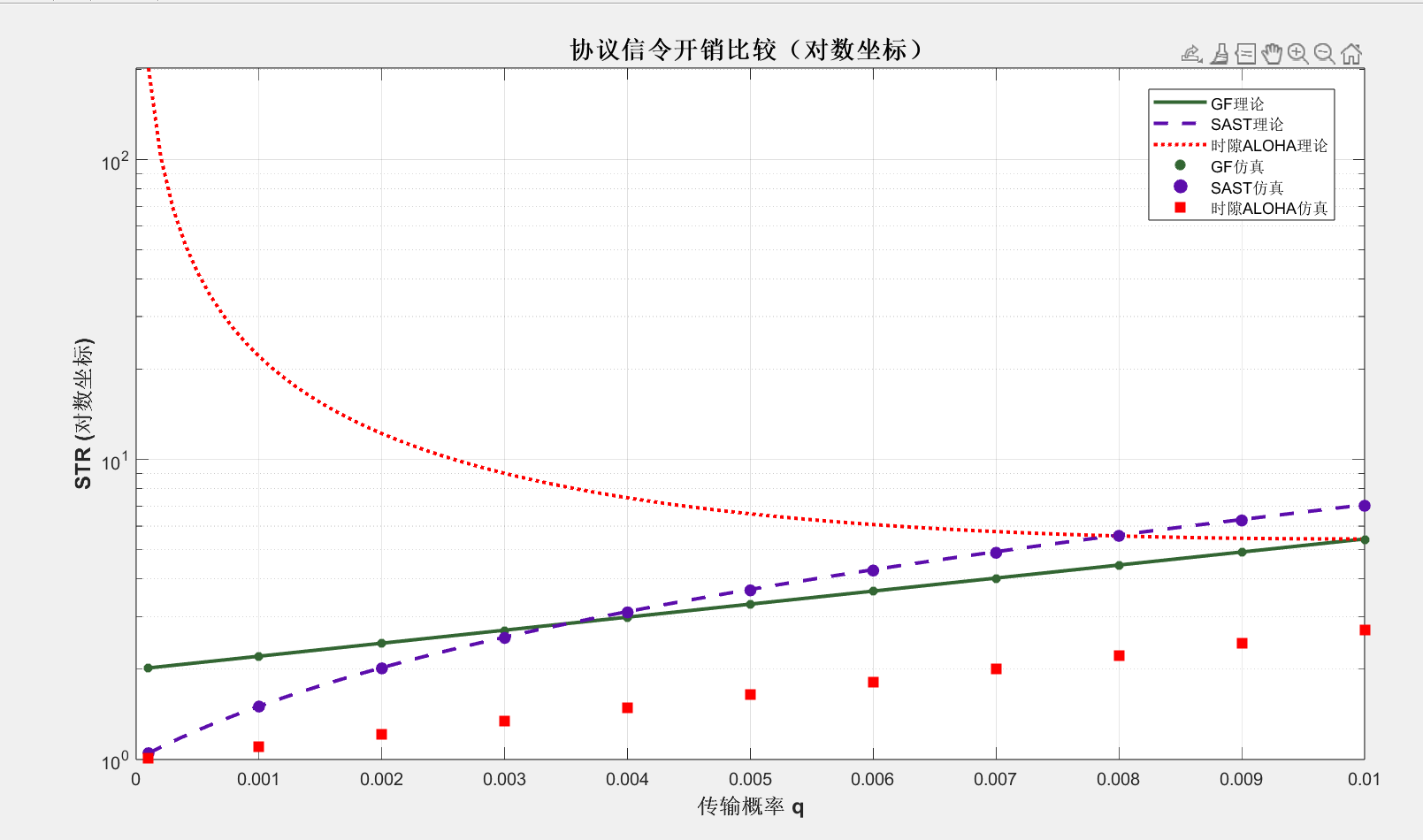
分析：仿真值趋势基本没有问题，但理论值有很大问题，还需要找到更准确理论估计STR值

公平性指标

时隙ALOHA协议公平性仿真思路阐述

1. 仿真目标

本函数旨在通过蒙特卡洛仿真方法，评估时隙ALOHA协议 在多节点竞争环境下的公平性表现，具体计算Jain公平性指数来衡量各节点获得传输机会的均等程度。

2. 核心仿真框架

2.1 状态初始化

matlab 复制代码

Node_state = zeros(Node_num, 2);
% 第1列：当前时隙传输标志 (0/1)
% 第2列：节点数据包队列长度

二维状态矩阵：同时跟踪节点的瞬时传输状态和累积数据包数量
均匀到达率 ：lambda = Lambda_total / Node_num 假设所有节点具有相同的业务负载

2.2 四步迭代流程（每个时隙）

步骤1：数据包到达过程

matlab 复制代码

for i = 1:Node_num
    if rand() <= lambda
        Node_state(i,2) = Node_state(i,2) + 1;  % 队列长度+1
    end
end

伯努利过程 ：每个节点独立地以概率λ产生新数据包
队列累积：模拟节点的业务负载积累

步骤2：传输决策机制

matlab 复制代码

transmitting_nodes = [];
for i = 1:Node_num
    if Node_state(i,2) > 0 && rand() <= q
        Node_state(i,1) = 1;                    % 设置传输标志
        transmitting_nodes = [transmitting_nodes, i];  % 记录传输节点
        Total_attempt = Total_attempt + 1;      % 总尝试次数统计
    end
end

双重条件 ：
1. 节点必须有数据包待传输 (Node_state(i,2) > 0)
2. 以概率q决定是否在当前时隙尝试传输
关键特性：每个节点的传输决策完全独立，无协调机制

步骤3：冲突检测与处理

matlab 复制代码

if length(transmitting_nodes) == 1
    % 成功传输：恰好一个节点传输
    node_transmit = transmitting_nodes(1);
    Total_success = Total_success + 1;
    Node_state(node_transmit,2) = Node_state(node_transmit,2) - 1;  % 队列减1
    node_success(node_transmit) = node_success(node_transmit) + 1;  % 成功计数
else
    % 冲突情况：0个或多个节点同时传输
    node_transmit = 0;  % 无成功传输
end

纯ALOHA特性 ：
- 成功条件：当且仅当恰好一个节点传输
- 冲突条件：0个（空闲）或多个（碰撞）节点传输都导致无成功传输
无重传机制 ：冲突的数据包直接丢失，不进入重传流程 （后面会补充证明不重传是合理的）

步骤4：状态重置与信令统计

matlab 复制代码

for i = 1:Node_num
    if Node_state(i,1) > 0
        signaling_count = signaling_count + 1;  % 信令开销统计
        Node_state(i,1) = 0;                    % 重置传输标志
    end
end

时隙边界处理：每个时隙结束后清除所有节点的传输状态
信令开销：每次传输尝试都计入信令成本（无论成功与否）

3. 公平性评估方法

Jain公平性指数计算

matlab 复制代码

fairness = jain_fairness_index(node_success);

输入：各节点在仿真期间的总成功传输次数向量
计算公式 ： J ( x 1 , x 2 , . . . , x n ) = ( ∑ i = 1 n x i ) 2 n ⋅ ∑ i = 1 n x i 2 J(x_1,x_2,...,x_n) = \frac{(\sum_{i=1}^n x_i)^2}{n \cdot \sum_{i=1}^n x_i^2} J(x1,x2,...,xn)=n⋅∑i=1nxi2(∑i=1nxi)2
物理意义 ：度量各节点获得服务机会的均等程度
- 1.0：完全公平（所有节点成功次数相同）
- 接近0：极度不公平（少数节点垄断资源）

4. 仿真参数意义

q：传输概率，控制网络负载和冲突概率
Lambda_total：系统总到达率，反映业务强度
Node_num：竞争节点数量，影响冲突概率
Total_slot：仿真时长，确保统计可靠性

5. 协议特性体现

完全分布式：无中心协调，各节点独立决策
随机接入 ：通过概率q实现随机退避
冲突不可避免：多个节点同时传输必然导致冲突
简单但低效：协议简单但吞吐量受限于冲突概率

这种仿真方法能够有效揭示时隙ALOHA协议在公平性方面的固有局限性，为与其他协议（如GF、SAST）的对比提供基准数据。

以下解释为什么在这个特定的公平性仿真中步骤三冲突检测与处理不实现重传机制是合理的，以及这背后的仿真设计哲学。

1. 仿真目标决定模型复杂度

核心目标：公平性比较

本仿真的主要目的 是比较不同协议（GF、SAST、ALOHA）的公平性
公平性 关注的是：在相同条件下，各节点获得传输机会的相对比例
重传机制会影响绝对性能，但不太可能改变协议间的相对公平性排序

控制变量原则

为了公平比较，所有协议应该在相同的基础机制下运行：

相同的到达过程
相同的传输概率q
相同的冲突处理逻辑

如果只为ALOHA添加重传，会破坏比较的公平性。

2. 理论完整性考虑

纯ALOHA协议定义

在经典的纯时隙ALOHA理论分析中：

matlab 复制代码

% 经典ALOHA吞吐量公式：S = G × e^(-G)
% 其中G为总负载，S为吞吐量

这个经典理论模型通常不考虑重传，而是假设：

冲突的数据包立即丢失
新数据包持续到达替代丢失的包

饱和条件假设

代码中明确注释了Lambda_total = 1; % 饱和情况，这意味着：

节点始终有数据要发送
丢失个别数据包不影响节点的持续竞争能力
公平性测量基于长期的成功传输比例

3. 仿真设计的合理性

公平性指标的鲁棒性

matlab 复制代码

% Jain公平性指数关注的是相对比例
fairness = (sum(node_success)^2) / (Node_num * sum(node_success.^2));

即使添加重传机制：

成功次数多的节点仍然成功次数多
成功次数少的节点仍然成功次数少
相对排名基本不变

计算复杂度与收敛性

matlab 复制代码

Total_slot = 2e6;  % 200万时隙，已足够统计收敛

添加重传会：

显著增加仿真时间
需要更复杂的退避算法设计
可能引入新的参数（退避窗口等），使比较更复杂

4. 与真实系统的对应关系

抽象层次的选择

这个仿真工作在MAC层公平性的抽象层次：

✅ 包含：竞争机制、冲突检测
❌ 不包含：重传策略、应用层业务模型

真实系统的映射

在真实系统中，ALOHA类的重传通常：

matlab 复制代码

% 真实系统可能的重传逻辑（伪代码）
if transmission_failed:
    backoff_time = random(0, CW)  % 退避窗口
    wait(backoff_time)           % 退避延迟
    retry_count = retry_count + 1

但这种重传机制：

不影响公平性本质：所有节点使用相同的退避算法
可能被其他因素掩盖：实际系统中还有功率控制、信道质量等

5. 替代解释视角

实际上，当前仿真隐式地包含了重传概念：

matlab 复制代码

% 当前逻辑：节点持续尝试直到成功
if Node_state(i,2) > 0 && rand() <= q
    % 只要队列中有包，就会持续尝试
    % 这相当于"立即重传"的极端情况

6. 如果需要更真实的仿真

如果确实需要包含重传，建议的改进：

matlab 复制代码

function [fairness, node_success] = ALOHA_fairness_with_retry(q, Lambda_total, Node_num, Total_slot)
    % 添加重传计数和退避机制
    retry_count = zeros(Node_num, 1);
    max_retry = 5;  % 最大重传次数
    CW_min = 4;     % 最小退避窗口
    
    for t = 1:Total_slot
        % 传输决策：考虑退避状态
        for i = 1:Node_num
            if Node_state(i,2) > 0 && retry_count(i) == 0 && rand() <= q
                % 新传输或退避结束的传输
                % ... 传输逻辑
            elseif retry_count(i) > 0
                % 退避计数减1
                retry_count(i) = retry_count(i) - 1;
            end
        end
        
        % 冲突处理：设置退避
        if collision_detected
            retry_count(collided_nodes) = random_backoff(CW_min, retry_count);
            % 超过最大重传次数的包被丢弃
            packets_dropped = (retry_count > max_retry);
        end
    end
end

结论

在当前公平性比较 的特定目标下，省略重传机制是合理的设计选择，因为：

不影响核心结论：协议间的相对公平性排序不会因重传而改变
保持比较公平：所有协议在相同简化条件下比较
计算效率：避免不必要的复杂度
理论一致性 ：与经典ALOHA分析模型保持一致
如果研究目标是绝对性能评估 或重传策略优化 ，那么添加重传机制就是必要的。但就公平性比较这一特定目标而言，当前设计是充分且合理的。

代码与结果

Main5.m：

matlab 复制代码

clc; clear; close all;
%% 公平性仿真比较：GF vs SAST vs 时隙ALOHA

ACB_bw_simu = [0.0001, 0.001:0.001:0.01];
Lambda_total = 1; % 饱和情况
Node_num = 100;
Total_slot = 2e6;

% 运行三种协议的公平性仿真
fairness1_simu = zeros(size(ACB_bw_simu));
fairness3_simu = zeros(size(ACB_bw_simu)); 
fairness4_simu = zeros(size(ACB_bw_simu));

for k = 1:length(ACB_bw_simu)
    q = ACB_bw_simu(k);
    
    % GF协议公平性仿真
    [fairness1_simu(k), ~] = GF_fairness(q, Lambda_total, Node_num, Total_slot);
    
    % SAST协议公平性仿真
    [fairness3_simu(k), ~] = SAST_fairness(q, Lambda_total, Node_num, Total_slot);
    
    % 时隙ALOHA公平性仿真
    [fairness4_simu(k), ~] = ALOHA_fairness(q, Lambda_total, Node_num, Total_slot);
end

%% 画图 - 公平性比较
figure('Units', 'normalized', 'Position', [0.1, 0.1, 0.6, 0.5]);
hold on;

% 颜色配置
figcol = cell(1,3);
figcol{1} = '#336633';  % GF - 绿色
figcol{2} = '#5C0DAC';  % SAST - 紫色
figcol{3} = '#FF0000';  % 时隙ALOHA - 红色

% 标记形状配置
figshape = cell(1,3);
figshape{1} = '*';
figshape{2} = 'o'; 
figshape{3} = 'square';

linewidth = 2;
markersize = 8;

% 绘制公平性曲线 - 简化绘图，避免重复绘制
h1 = plot(ACB_bw_simu, fairness1_simu, '-', 'Color', figcol{1}, 'LineWidth', linewidth, ...
    'Marker', figshape{1}, 'MarkerSize', markersize, 'MarkerEdgeColor', figcol{1});
h2 = plot(ACB_bw_simu, fairness3_simu, '--', 'Color', figcol{2}, 'LineWidth', linewidth, ...
    'Marker', figshape{2}, 'MarkerSize', markersize, 'MarkerEdgeColor', figcol{2});
h3 = plot(ACB_bw_simu, fairness4_simu, ':', 'Color', figcol{3}, 'LineWidth', linewidth, ...
    'Marker', figshape{3}, 'MarkerSize', markersize, 'MarkerEdgeColor', figcol{3});

hold off;

% 图形美化
xlim([0, max(ACB_bw_simu)]);
ylim([0, 1]);

% 修正字体设置 - 使用支持中文的字体
xlabel('传输概率 q', 'FontSize', 12, 'FontWeight', 'bold');
ylabel('Jain公平性指数', 'FontSize', 12, 'FontWeight', 'bold');

% 图例设置 - 使用支持中文的字体
legend([h1, h2, h3], 'GF协议', 'SAST协议', '时隙ALOHA', ...
    'Location', 'best', 'FontSize', 10);

% 坐标轴设置 - 移除字体名称设置，使用系统默认字体
ax = gca;
ax.FontSize = 11;
ax.LineWidth = 1;
ax.Box = 'on';
ax.GridLineStyle = '-';
ax.GridAlpha = 0.3;
grid on;

% 标题（可选）
title('协议公平性比较', 'FontSize', 14, 'FontWeight', 'bold');

% 保存图形
saveas(gcf, 'fairness_comparison.png');
save('fairness_comparison.mat');

%% 如果中文仍然显示有问题，使用以下替代方案：
% 方案1：使用英文标签
% xlabel('Transmission Probability q', 'FontSize', 12, 'FontWeight', 'bold');
% ylabel('Jain Fairness Index', 'FontSize', 12, 'FontWeight', 'bold');
% legend([h1, h2, h3], 'GF Protocol', 'SAST Protocol', 'Slotted ALOHA', ...
%     'Location', 'best', 'FontSize', 10);
% title('Protocol Fairness Comparison', 'FontSize', 14, 'FontWeight', 'bold');

% 方案2：设置支持中文的字体
% set(gca, 'FontName', 'SimHei');  % 黑体，通常支持中文
% xlabel('传输概率 q', 'FontSize', 12, 'FontWeight', 'bold', 'FontName', 'SimHei');
% ylabel('Jain公平性指数', 'FontSize', 12, 'FontWeight', 'bold', 'FontName', 'SimHei');
% legend([h1, h2, h3], 'GF协议', 'SAST协议', '时隙ALOHA', ...
%     'Location', 'best', 'FontSize', 10, 'FontName', 'SimHei');
% title('协议公平性比较', 'FontSize', 14, 'FontWeight', 'bold', 'FontName', 'SimHei');

保存在Slotted公平性.fig

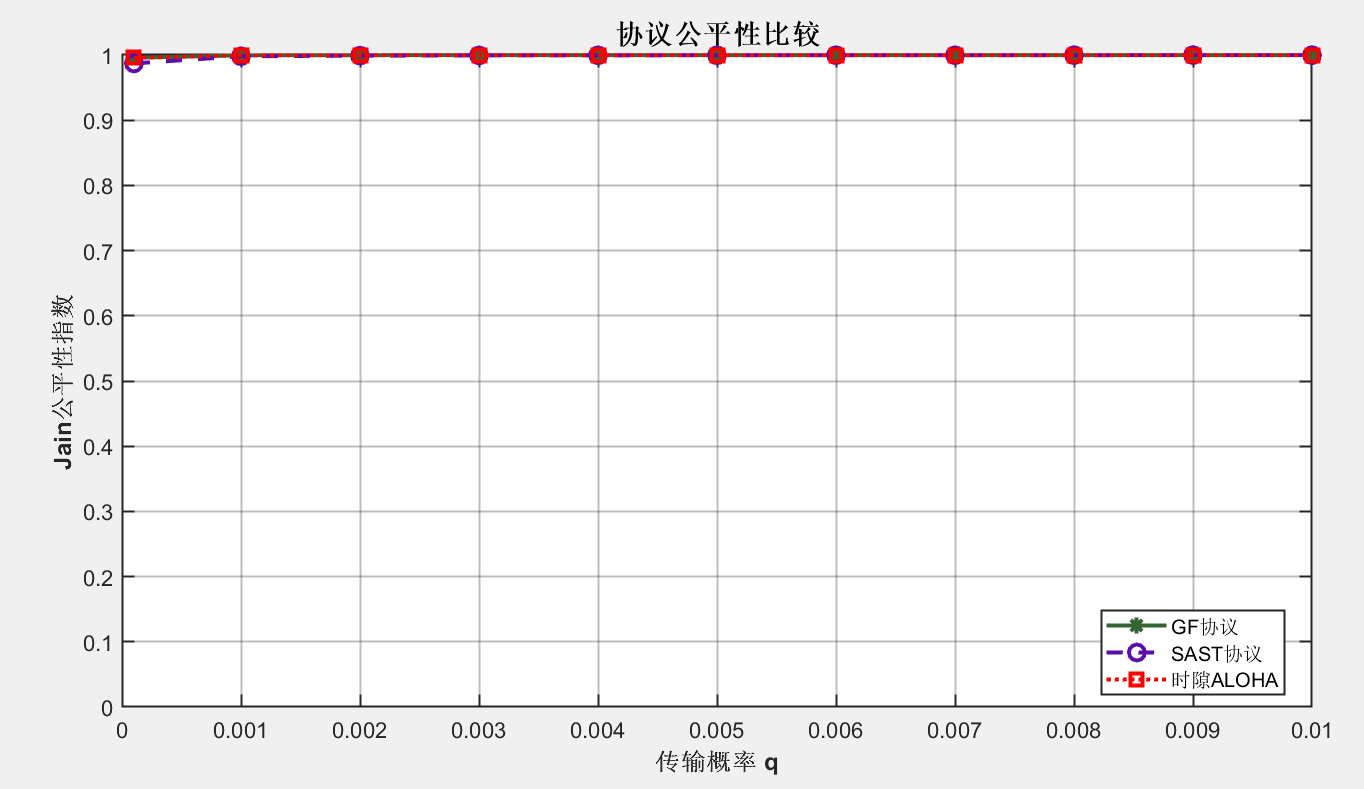
分析：有图像可以看出slotted Aloha的公平性指数很好，可以认为协议很公平

时延性

时隙ALOHA协议时延仿真思路

1. 仿真目标与核心改进

核心目标

测量数据包在ALOHA系统中的端到端时延，从到达时刻到成功传输时刻的时间间隔（以时隙为单位）。

相对于公平性仿真的改进

数据包级跟踪：为每个数据包记录到达时间，实现精确时延测量
队列管理：实现FIFO（先进先出）队列调度
内存优化：预分配数组提高仿真效率

2. 关键数据结构设计

matlab 复制代码

% 数据包级跟踪系统
arrival_times = zeros(max_packets, 1);   % 每个包的到达时间戳
node_for_packet = zeros(max_packets, 1); % 每个包的所属节点ID

% 节点级状态管理
next_tx_index = ones(Node_num, 1);       % 每个节点下一个要传输的包索引
Node_state = zeros(Node_num, 2);         % [传输状态, 队列长度]

这种双层级设计是仿真的核心创新：

宏观：节点状态跟踪
微观：数据包生命周期跟踪

3. 四步仿真流程（每时隙）

步骤1：数据包到达 - 向量化处理

matlab 复制代码

arrival_flags = (rand(Node_num, 1) <= lambda);
nodes_arrived = find(arrival_flags);

向量化伯努利过程：同时生成所有节点的到达事件
批量记录：一次性记录所有新到达数据包的信息
队列更新：对应节点队列长度增加

步骤2：传输决策 - 条件概率机制

matlab 复制代码

has_packets = (Node_state(:, 2) > 0);
will_transmit = has_packets & (rand(Node_num, 1) <= q);

双重条件筛选 ：
1. 节点必须有数据包等待传输
2. 以概率q决定是否尝试传输
统计计数：记录总尝试次数

步骤3：冲突检测与时延计算

matlab 复制代码

if num_transmitting == 1
    node_transmit = find(will_transmit, 1);
    % 计算时延
    pkt_idx = next_tx_index(node_transmit);
    delay = t - arrival_times(pkt_idx);

成功条件：恰好一个节点传输
时延计算 ：当前时隙 - 到达时隙
队列管理 ：
- 成功传输后队列减1
- 节点传输指针向前移动

步骤4：状态重置与信令统计

matlab 复制代码

signaling_count = signaling_count + num_transmitting;
Node_state(will_transmit, 1) = 0;

信令开销：每次传输尝试都计入成本
状态清理：为下一时隙做准备

4. 时延测量的精确性保障

FIFO队列保证

matlab 复制代码

% 每个节点维护传输指针，确保按到达顺序传输
pkt_idx = next_tx_index(node_transmit);  % 总是传输队列中最老的数据包
next_tx_index(node_transmit) = next_tx_index(node_transmit) + 1;

数据包生命周期完整跟踪

出生：记录到达时间戳
服务：成功传输时计算时延
统计：只对成功传输的数据包计算时延

5. 性能优化策略

内存预分配

matlab 复制代码

max_packets = round(Lambda_total * Total_slot * 1.1) + 1;

避免动态数组增长的开销
预留10%余量防止数组越界

向量化操作

matlab 复制代码

arrival_flags = (rand(Node_num, 1) <= lambda);  % 替代循环

大幅提升仿真速度
减少循环开销

6. 统计指标设计

主要输出

avg_delay：平均时延（核心指标）
throughput：系统吞吐量（成功包/时隙）
signaling_overhead：信令开销密度

辅助统计

total_success：总成功传输数
total_attempt：总尝试次数
delay_count：有效时延样本数

7. 物理意义与现实对应

这个仿真精确反映了真实网络中的时延组成：

排队时延：数据包在节点队列中等待的时间
传输时延：从开始尝试到成功传输的时间
冲突开销：因冲突导致的重复尝试时间

总结

这个时延仿真通过精细的数据包生命周期跟踪 和优化的向量化实现 ，提供了对时隙ALOHA协议时延性能的准确评估。其设计思路体现了从"能否传输"（公平性）到"多快传输"（时延）的性能分析深化，为协议性能的全面理解提供了重要支撑。

这种仿真方法能够揭示传输概率q、到达率Lambda_total等参数对系统时延的影响规律，为网络参数优化提供理论依据。

ALOHA_delay.m

matlab 复制代码

function [avg_delay, delay_stats] = ALOHA_delay(q, Lambda_total, Node_num, Total_slot)
% 时隙ALOHA协议时延测量函数（优化高速版）
% 输入：
%   q: 传输概率
%   Lambda_total: 总到达率（包/时隙）
%   Node_num: 节点数量
%   Total_slot: 仿真总时隙数
% 输出：
%   avg_delay: 平均时延（时隙）
%   delay_stats: 统计信息结构体

    % 参数初始化
    lambda = Lambda_total / Node_num;

    % ==================== 预分配内存 ====================
    % 估计最大数据包数（留10%余量）
    max_packets = round(Lambda_total * Total_slot * 1.1) + 1;
    arrival_times = zeros(max_packets, 1);           % 到达时间
    node_for_packet = zeros(max_packets, 1);         % 所属节点
    next_tx_index = ones(Node_num, 1);               % 每个节点下一个要传的包在全局数组中的索引
    current_pkt_idx = 1;                             % 当前已生成的包总数（全局）

    % 节点状态: [is_transmitting, queue_length]
    Node_state = zeros(Node_num, 2);

    % 统计变量
    total_delay = 0;
    delay_count = 0;
    Total_success = 0;
    Total_attempt = 0;
    signaling_count = 0;

    % ==================== 主循环 ====================
    for t = 1:Total_slot

        % --- 1. 数据包到达：向量化生成 ---
        arrival_flags = (rand(Node_num, 1) <= lambda);
        if any(arrival_flags)
            nodes_arrived = find(arrival_flags);
            num_arrivals = length(nodes_arrived);

            % 更新队列长度
            Node_state(nodes_arrived, 2) = Node_state(nodes_arrived, 2) + 1;

            % 批量记录到达信息
            idx_range = current_pkt_idx : current_pkt_idx + num_arrivals - 1;
            arrival_times(idx_range) = t;
            node_for_packet(idx_range) = nodes_arrived;
            current_pkt_idx = current_pkt_idx + num_arrivals;
        end

        % --- 2. 传输决策：哪些节点尝试发送（以概率 q）---
        % 条件：队列非空
        has_packets = (Node_state(:, 2) > 0);
        will_transmit = has_packets & (rand(Node_num, 1) <= q);

        num_transmitting = sum(will_transmit);
        Total_attempt = Total_attempt + num_transmitting;

        % 标记传输状态
        Node_state(will_transmit, 1) = 1;

        % --- 3. 冲突检测：仅当只有一个节点尝试时才成功 ---
        if num_transmitting == 1
            node_transmit = find(will_transmit, 1);  % 成功
            Total_success = Total_success + 1;
            Node_state(node_transmit, 2) = Node_state(node_transmit, 2) - 1;  % 减队列

            % 计算时延
            pkt_idx = next_tx_index(node_transmit);
            if pkt_idx <= max_packets && node_for_packet(pkt_idx) == node_transmit
                delay = t - arrival_times(pkt_idx);
                total_delay = total_delay + delay;
                delay_count = delay_count + 1;
                next_tx_index(node_transmit) = next_tx_index(node_transmit) + 1;
            end
        else
            node_transmit = 0;  % 冲突或无传输
        end

        % --- 4. 信令开销 + 状态重置 ---
        % 每个尝试发送的节点产生 1 单位信令（发送动作）
        signaling_count = signaling_count + num_transmitting;

        % 重置所有节点的传输标志
        Node_state(will_transmit, 1) = 0;

    end

    % ==================== 输出结果 ====================
    if delay_count > 0
        avg_delay = total_delay / delay_count;
    else
        avg_delay = Inf;
    end

    % 返回统计信息
    delay_stats.total_delay = total_delay;
    delay_stats.delay_count = delay_count;
    delay_stats.throughput = Total_success / Total_slot;
    delay_stats.total_success = Total_success;
    delay_stats.total_attempt = Total_attempt;
    delay_stats.signaling_overhead_per_slot = signaling_count / Total_slot;

end

Main6.m

matlab 复制代码

clc;clear;close all;
%% 时延仿真比较：GF vs SAST vs 时隙ALOHA

ACB_bw_simu = [0.0001,0.001:0.001:0.01];
Lambda_total = 1; % 饱和情况
Node_num = 100;
Total_slot = 2e6;

% 运行三种协议的时延仿真
delay1_simu = zeros(size(ACB_bw_simu));
delay3_simu = zeros(size(ACB_bw_simu));
delay4_simu = zeros(size(ACB_bw_simu));

for k = 1:length(ACB_bw_simu)
    q = ACB_bw_simu(k);
    
    % GF协议时延仿真
    [delay1_simu(k), ~] = GF_delay(q, Lambda_total, Node_num, Total_slot);
    
    % SAST协议时延仿真
    [delay3_simu(k), ~] = SAST_delay(q, Lambda_total, Node_num, Total_slot);
    
    % 时隙ALOHA时延仿真
    [delay4_simu(k), ~] = ALOHA_delay(q, Lambda_total, Node_num, Total_slot);
end

%% 画图 - 时延比较
figure 
hold on;

% 颜色配置
figcol = cell(1,3);
figcol{1} = '#336633';  % GF - 绿色
figcol{2} = '#5C0DAC';  % SAST - 紫色
figcol{3} = '#FF0000';  % 时隙ALOHA - 红色

% 标记形状配置
figshape = cell(1,3);
figshape{1} = '*';
figshape{2} = 'O';
figshape{3} = 'square';

linewidth = 2;
markersize = 80;

% 绘制时延曲线
semilogy(ACB_bw_simu, delay1_simu, '-', 'color', figcol{1}, 'LineWidth', linewidth);
scatter(ACB_bw_simu, delay1_simu, markersize, 'MarkerEdgeColor', figcol{1}, ...
    'Marker', figshape{1}, 'LineWidth', linewidth);

semilogy(ACB_bw_simu, delay3_simu, '--', 'color', figcol{2}, 'LineWidth', linewidth);
scatter(ACB_bw_simu, delay3_simu, markersize, 'MarkerEdgeColor', figcol{2}, ...
    'Marker', figshape{2}, 'LineWidth', linewidth);

semilogy(ACB_bw_simu, delay4_simu, ':', 'color', figcol{3}, 'LineWidth', linewidth);
scatter(ACB_bw_simu, delay4_simu, markersize, 'MarkerEdgeColor', figcol{3}, ...
    'Marker', figshape{3}, 'LineWidth', linewidth);

hold off;
xlim([0, max(ACB_bw_simu)]);

% 设置中文标签（使用支持中文的字体，关闭latex解释器）
xlabel('传输概率', 'Interpreter', 'none', 'FontName', 'SimHei', 'fontsize', 14);
ylabel('平均时延 (时隙)', 'Interpreter', 'none', 'FontName', 'SimHei', ...
    'rotation', 0, 'Horizontalalignment', 'right', 'fontsize', 14);

% 添加中文标题
title('三种协议的时延仿真比较', 'Interpreter', 'none', 'FontName', 'SimHei', 'fontsize', 16);

% 设置图例（支持中文）
legend('GF协议', 'SAST协议', '时隙ALOHA', 'Location', 'best', ...
    'Interpreter', 'none', 'FontName', 'SimHei', 'fontsize', 12);

% 设置坐标轴字体（支持中文）
set(gca, 'position', [0.15, 0.15, 0.7, 0.7], 'LineWidth', 0.5, ...
    'fontsize', 14, 'FontName', 'SimHei');  % 改为SimHei支持中文
set(gcf, 'unit', 'normalized', 'position', [.2, .2, 0.4, 0.45]);
grid on;
box on;

save('delay_comparison.mat');

结果：

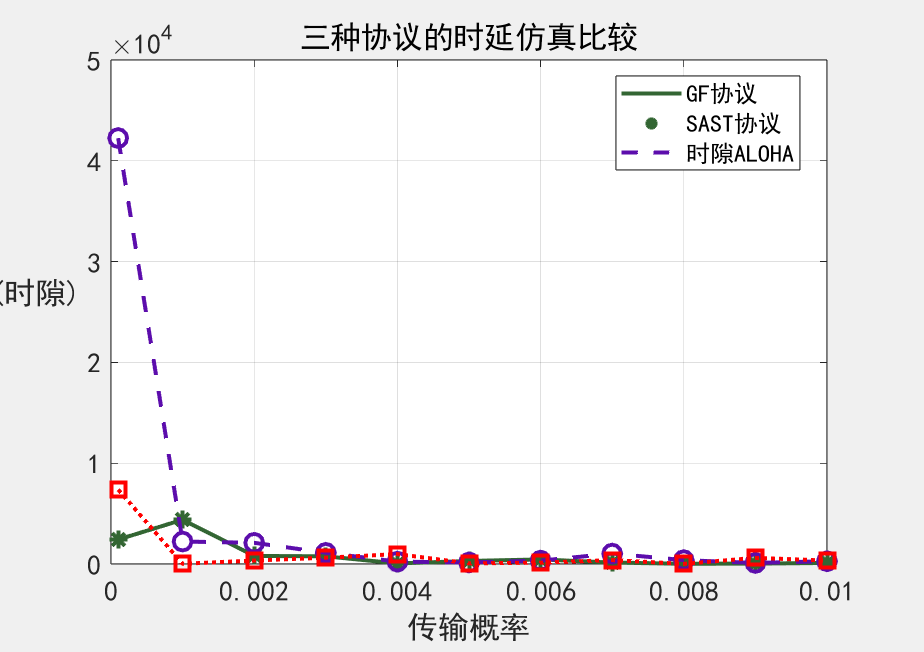
分析：

在q较小的时候，slotted时延仿真效果并不好，但在q较大的时候时延性较低，仿真效果较好，且slotted Aloha在时延性指标中与SAST没有明显差别