文章目录
- [1 概述](#1 概述)
- [2 损失函数](#2 损失函数)
- [3 API 使用](#3 API 使用)
- [4 多分类](#4 多分类)
-
- [4.1 OvO OvR](#4.1 OvO OvR)
- [4.2 Softmax 回归](#4.2 Softmax 回归)
1 概述
逻辑回归(Logistic Regression)尽管名字中含有"回归",但逻辑回归实际上是一种分类算法,用于处理二分类问题。逻辑回归通过将线性回归的输出作为输入,映射到[0,1]区间,来表示某个类别的概率。
常用的映射函数是 sigmoid 函数: 𝑓 ( 𝑥 ) = 1 1 + 𝑒 − 𝑥 𝑓(𝑥)=\frac{1}{1+𝑒^{−𝑥}} f(x)=1+e−x1,将线性回归的输出作为输入会得到 {0, 1} 的输出。
𝑃 ( 𝑦 = 1 ∣ x ) = 1 1 + e − ( w T x + b ) 𝑃(𝑦=1∣x)=\frac{1}{1+e^{-(w^Tx+b)}} P(y=1∣x)=1+e−(wTx+b)1
𝑃 ( 𝑦 = 1 ∣ x ) 𝑃(𝑦=1∣x) P(y=1∣x)表示输出为 1 类的概率,根据逻辑回归结果和阈值来确认最终预测结果,若逻辑回归结果大于阈值则输出为 1类,反之输出为 0 类。
0.5 0 0.7 0.5 0.5 0.9 0.1 1 0.6 0.6 0.1 0 \] \[ − 1 2 0.5 \] = \[ − 0.15 0.95 2.2 − 0.4 \] → s i g m o i d \[ 0.46257015 0.72111518 0.90024951 0.40131234 \] → 与阈值 0.5 比较 \[ 0 1 1 0 \] \\begin{aligned} \& \\begin{bmatrix} 0.5 \& 0 \& 0.7 \\\\ 0.5 \& 0.5 \& 0.9 \\\\ 0.1 \& 1 \& 0.6 \\\\ 0.6 \& 0.1 \& 0 \\end{bmatrix} \\begin{bmatrix} -1 \\\\ 2 \\\\ 0.5 \\end{bmatrix}=\\quad \\begin{bmatrix} -0.15 \\\\ 0.95 \\\\ 2.2 \\\\ -0.4 \\end{bmatrix}\\quad\\xrightarrow{\\mathrm{sigmoid}} \\begin{bmatrix} 0.46257015 \\\\ 0.72111518 \\\\ 0.90024951 \\\\ 0.40131234 \\end{bmatrix}\\xrightarrow{\\text{与阈值 }0.5\\text{ 比较}}\\quad \\begin{bmatrix} 0 \\\\ 1 \\\\ 1 \\\\ 0 \\end{bmatrix} \\end{aligned} 0.50.50.10.600.510.10.70.90.60 −120.5 = −0.150.952.2−0.4 sigmoid 0.462570150.721115180.900249510.40131234 与阈值 0.5 比较 0110 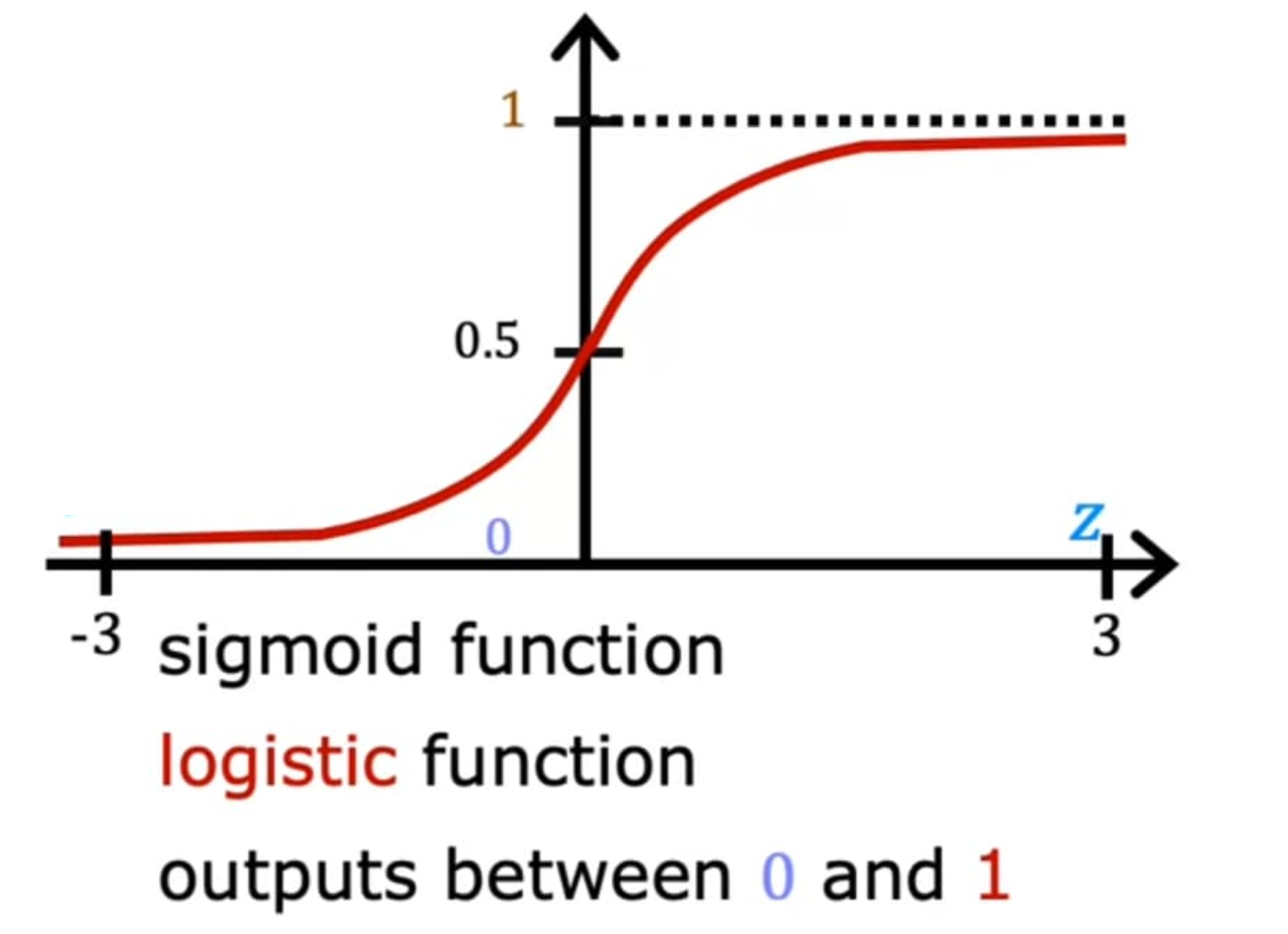 > 实际逻辑回归是一个翻译错误,Logistic 并没有回归的意思,而是来自统计学中的 log odds(对数几率),后来发明了一个词 Logit 来描述,实际应为对数几率回归,或对率回归。 ## 2 损失函数 逻辑回归的损失函数通常使用对数损失(Log Loss),也称为二元交叉熵损失(Binary Cross-Entropy Loss) , 用于衡量模型输出的概率分布与真实标签之间的差距。 逻辑回归的损失函数来源于最大似然估计(MLE)。 对数似然: log L ( y , F ( X ) ) = ∑ i = 1 n y i l o g p x i + ( 1 − y i ) l o g ( 1 − p x i ) \\log L({y,F(X)})=\\sum_{i=1}\^ny_i\\mathrm{log}\\,p_{x_i}+(1-y_i)\\mathrm{log}\\,(1-p_{x_i}) logL(y,F(X))=i=1∑nyilogpxi+(1−yi)log(1−pxi) y i y_i yi 是第 i i i 个样本的真实值(0 或 1), p x i p_{x_i} pxi 是第 i i i 个样本属于类别 1 的概率。当 y i y_i yi 为 1 时,右边消掉,当 y i y_i yi 为 0 时,左边消掉,概率越低,把握越小,则 log 值越小,当似然函数最大时,损失最小。 拟合就是求似然函数的最大值,为了方便优化,令损失函数为: L o s s = − 1 n ∑ i = 1 n y i l o g p x i + ( 1 − y i ) l o g ( 1 − p x i ) Loss=-\\frac{1}{n}\\sum_{i=1}\^ny_i\\mathrm{log}\\,p_{x_i}+(1-y_i)\\mathrm{log}\\,(1-p_{x_i}) Loss=−n1i=1∑nyilogpxi+(1−yi)log(1−pxi) 加上负号,求解损失函数的最小值即可, 1 n \\frac{1}{n} n1 则类似均方误差中的平均。 ## 3 API 使用 ```python from sklearn.linear_model import LogisticRegression model = LogisticRegression() model.fit(X_train, X_test) ``` * `penalty`:指定正则化类型,用于控制模型复杂度,防止过拟合,默认值为 `l2`。 * `C`:正则化强度的倒数,默认值为 `1.0`。较小的 `C` 值会加强正则化(更多限制模型复杂度),较大的 `C` 值会减弱正则化(更注重拟合训练数据)。 * `solver`:指定优化算法,默认值为 `lbfgs`,可选值包括: * `'lbfgs'`: 拟牛顿法(默认),仅支持 L2正则化 * `'newton-cg'`: 牛顿法,仅支持 L2正则化 * `'liblinear'`: 坐标下降法,适用于小数据集,支持 L1和 L2正则化 * `'sag'`: 随机平均梯度下降,适用于大规模数据集,仅支持 L2正则化 * `'saga'`: 改进的随机梯度下降,适用于大规模数据,支持 L1、L2和 ElasticNet正则化 * `multi_class`:指定多分类问题的处理方式,默认值为 `'auto'`,根据数据选择 `'ovr'` 或 `'multinomial'`,前者表示一对多策略,适合二分类或多分类的基础情况,后者表示多项式回归策略,适用于多分类问题,需与 `'lbfgs'`、`'sag'` 或 `'saga'` 搭配使用。 * `fit_intercept`:是否计算截距(偏置项),默认值为 `True`。 * `class_weight`:类别权重,处理类别不平衡问题,默认值为 `None`,设置为 `'balanced'`可以根据类别频率自动调整权重。 ## 4 多分类 逻辑回归通常用于二分类问题,但可以通过一对多(One-vs-Rest,OvR)、一对一(One-vs-One, OvO)以及 Softmax 回归(Multinomial Logistic Regression,多项逻辑回归)来扩展到多分类任务。 ### 4.1 OvO OvR * OvO 存储开销和测试时间大,训练时间短 * OvR 存储开销和测试时间小,训练时间长 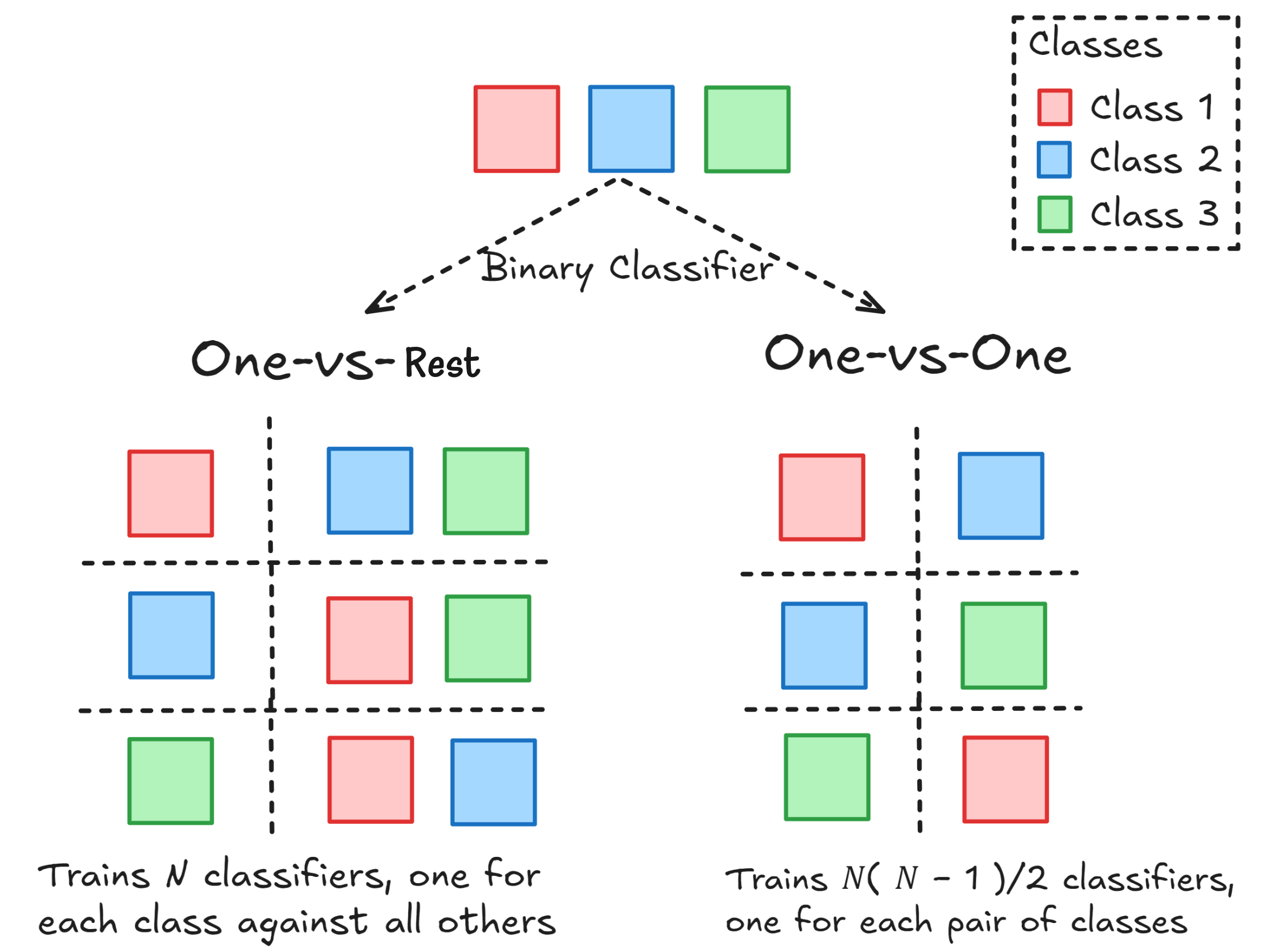 ```python from sklearn.linear_model import LogisticRegression model = LogisticRegression( multi_class='ovr' # 设置 ovr 或者 ovo ) ``` `multi_class`在后续版本中将会被废弃,取而代之的是一个新的类来实现 OvO、OvR。 ```python from sklearn.multiclass import OneVsOneClassifier, OneVsRestClassifier model1 = OneVsOneClassifier(estimator=LogisticRegression()) model2 = OneVsRestClassifier(estimator=LogisticRegression()) ``` ### 4.2 Softmax 回归 Softmax 回归(多项逻辑回归)直接扩展逻辑回归到多分类问题,使用 Softmax 函数将模型输出转化为概率分布。 对于类别 c: P ( y = c ∣ x ) = e β c T x ∑ j = 1 C e β j T x P(y=c\|x)=\\frac{e\^{\\beta_{c}\^{T}x}}{\\sum_{j=1}\^{C}e\^{\\beta_{j}\^{T}x}} P(y=c∣x)=∑j=1CeβjTxeβcTx 损失函数: L o s s = − 1 n ∑ i = 1 n ∑ c = 1 C I ( y i = c ) l o g P ( y i = c ∣ x i ) Loss=-\\frac{1}{n}\\sum_{i=1}\^{n}\\sum_{c=1}\^{C}I(y_{i}=c)\\mathrm{log}P(y_{i}=c\|x_{i}) Loss=−n1i=1∑nc=1∑CI(yi=c)logP(yi=c∣xi) 其中 𝐼 ( 𝑦 𝑖 = c ) 𝐼(𝑦_𝑖 =c) I(yi=c) 为示性函数,当 𝑦 𝑖 = c 𝑦_𝑖 =c yi=c 时值为 1,反之值为 0。 * 优点:只训练 1 个模型,计算高效,分类一致性更好。 * 缺点:计算 Softmax 需要对所有类别求指数,计算量较高。 ```python from sklearn.linear_model import LogisticRegression model = LogisticRegression(multi_class="multinomial") ``` 对于多分类问题,LogisticRegression 会自动使用 `multinomial`,因此 `multi_class` 参数可省略。整体来看,大多数情况 Softmax 更加优秀,这也是为什么要把 `multi_class` 移除。