文章目录
- 实例代码下载链接
-
- [ 顺序表实例代码](# 顺序表实例代码)
- [ 单链表表实例代码](# 单链表表实例代码)
- [ 双向链表实例代码](# 双向链表实例代码)
- 一、线性表
-
- [ 1、线性表(list):](# 1、线性表(list):)
- [ 2、线性表一般表示形式:](# 2、线性表一般表示形式:)
- [ 3、抽象数据类型线性表的定义:](# 3、抽象数据类型线性表的定义:)
- [ 顺序表和链表是指储存结构。](# 顺序表和链表是指储存结构。)
- [二、顺序表(Sequence List)](#二、顺序表(Sequence List))
-
- [ 1、简介:](# 1、简介:)
- [ 2、循序表的存储结构:](# 2、循序表的存储结构:)
- [ 3、初始化](# 3、初始化)
- [ 4、获取元素](# 4、获取元素)
- [ 5、查找元素](# 5、查找元素)
- [ 6、插入](# 6、插入)
- [ 7、删除](# 7、删除)
- [ 8、销毁,清空,检查为空](# 8、销毁,清空,检查为空)
- [ 9、顺序表的完整测试文件](# 9、顺序表的完整测试文件)
-
- [ 1)、SequenceList.h](# 1)、SequenceList.h)
- [ 2)、SequenceList.c](# 2)、SequenceList.c)
- [ 3)、main.c](# 3)、main.c)
- [ 4)、运行结果](# 4)、运行结果)
- [三、单链表(Single Linked List)](#三、单链表(Single Linked List))
-
- [ 1、单链表](# 1、单链表)
- [ 2、初始化](# 2、初始化)
- [ 3、创建链表(头插法)](# 3、创建链表(头插法))
- [ 4、创建链表(尾插法)](# 4、创建链表(尾插法))
- [ 5、获取元素](# 5、获取元素)
- [ 6、查找元素](# 6、查找元素)
- [ 7、插入元素](# 7、插入元素)
- [ 8、删除元素](# 8、删除元素)
- [ 9、总结插入和删除操作算法的不同](# 9、总结插入和删除操作算法的不同)
- [ 10、销毁链表](# 10、销毁链表)
- [ 11、单链表测试文件](# 11、单链表测试文件)
-
- [ 1)、SingleLinkedList.h](# 1)、SingleLinkedList.h)
- [ 2)、SingleLinkedList.c](# 2)、SingleLinkedList.c)
- [ 3)、main.c](# 3)、main.c)
- [ 4)、运行结果](# 4)、运行结果)
- [四、循环链表(Circular Linked List)](#四、循环链表(Circular Linked List))
-
- [ 循环链表的特点:](# 循环链表的特点:)
- [五、双向链表(Double Linked List)](#五、双向链表(Double Linked List))
-
- [ 1、数据类型](# 1、数据类型)
- [ 2、初始化](# 2、初始化)
- [ 3、创建双向链表](# 3、创建双向链表)
- [ 4、插入和删除](# 4、插入和删除)
- [ 5、双向链表测试文件](# 5、双向链表测试文件)
-
- [ 1)、DoubleLinkedList.h](# 1)、DoubleLinkedList.h)
- [ 2)、DoubleLinkedList.c](# 2)、DoubleLinkedList.c)
- [ 3)、main.c](# 3)、main.c)
- [ 4)、运行结果](# 4)、运行结果)
- 六、线性表其它操作
-
- [ 1、线性表合并](# 1、线性表合并)
- [ 2、有序表合并(并归排序的基础)](# 2、有序表合并(并归排序的基础))
- [ 3、有序链表合并](# 3、有序链表合并)
- [ 4、多项式创建 and 多项式相加](# 4、多项式创建 and 多项式相加)
实例代码下载链接
顺序表实例代码
通过网盘分享的文件:testSL.rar
链接: https://pan.baidu.com/s/108wdwJA_brTSdHKTtsSlDg?pwd=26gt 提取码: 26gt
单链表表实例代码
通过网盘分享的文件:testLL.rar
链接: https://pan.baidu.com/s/1W8hqq91IMXA7mZeMZcKEPg?pwd=vb75 提取码: vb75
双向链表实例代码
通过网盘分享的文件:testDL.rar
链接:https://pan.baidu.com/s/19lTytQF09lfH3LORM2BsaA?pwd=rs77 提取码: rs77
一、线性表
1、线性表(list):
具有相同数据类型的n(n>=0)个数的有限序列。
2、线性表一般表示形式:
L = (a1,a2,... ,ai,... ,an)
a1是第一个数据元素,称为表头元素,an是最后一个数据元素,称为表尾元素。除第一个元素外,每一个元素有且只有一个前驱。除最后一个元素外,每一个元素有且只有一个后驱。
线性表是一种逻辑结构,表示元素之间一对一的相邻关系。
3、抽象数据类型线性表的定义:
ADT List{
数据对象:D ={a;a:属于Elemset,(i=1,2...n,n≥0)}
数据关系:R={< ai.1,a¡>|a¡-1,a;属于D,(i=2,3.,n))
基本操作:
DestroyList(&L);
ListDelete(&L,i,&e);
Listlnsert(&L,i,e);
InitList(&L);
......
} ADT List
顺序表和链表是指储存结构。
二、顺序表(Sequence List)
1、简介:
线性表的顺序表示又称为顺序存储结构或者顺序映像。
顺序存储的定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。
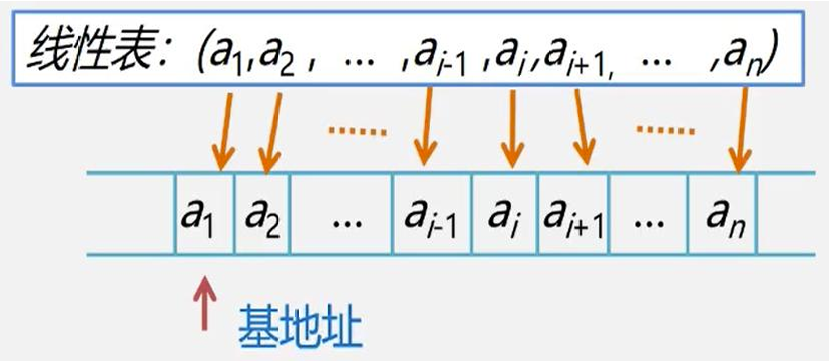
以元素在计算机内存中"物理位置相邻"来表示线性表中数据元素之间的逻辑关系。
线性表的第1个元素a1的存储位置,称作线性表的起始位置或基地址。
只要确定了存储线性表的起始位置,线性表中任一数据元素都可以随机存取,所以线性表的顺序结构是一种随机存取的存储结构。
特点:逻辑上相邻的数据元素,其物理次序也是相邻的。
2、循序表的存储结构:
c
#define SQLMAXSIZE 100
typedef int SqlElemType;
typedef struct __Sqlist {
SqlElemType *base;
int length; //当前长度
} Sqlist;3、初始化
c
Status InitSL(Sqlist *L, int length) {
L->base = (SqlElemType *)malloc(sizeof(SqlElemType) * SQLMAXSIZE);
if (!L->base)
return OVERFLOW;
L->length = 0;
for (int i = 1; i < length + 1; i++) {
SqlElemType e;
scanf(" %d", &e);
SqlInsert(L, i, e);
}
return OK;
}4、获取元素
c
Status GetElem(Sqlist *L, int position, SqlElemType *e) {
if (position < 1 || position > L->length)
return ERROR;
*e = L->base[position - 1];
return OK;
}5、查找元素
c
int LocateElem(Sqlist *L, SqlElemType e) {
for (int i = 0; i < L->length; i++) {
if (e == L->base[i])
return i + 1;
}
return 0; // 0代表查找元素不在循序表中
}
平均查找长度ASL(Average Search Length)
6、插入
c
Status SqlInsert(Sqlist *L, int position, SqlElemType e) {
if (position < 1 || position > L->length + 1)
return ERROR;
if (L->length == SQLMAXSIZE)
return OVERFLOW;
for (int i = L->length - 1; i >= position - 1; i--) { //注意需要把数组中的元素全部向右移动,需要从数组最右边的元素开始移动
L->base[i + 1] = L->base[i];
}
L->base[position - 1] = e;
L->length++;
return OK;
}7、删除
c
Status SqlDelete(Sqlist *L, int position, SqlElemType *e) {
if (position < 1 || position > L->length)
return ERROR;
for (int i = position; i < L->length; i++) {
L->base[i - 1] = L->base[i];
}
*e = L->base[position - 1];
L->length--;
return OK;
}8、销毁,清空,检查为空
c
Status SqlDelete(Sqlist *L, int position, SqlElemType *e) {
if (position < 1 || position > L->length)
return ERROR;
for (int i = position; i < L->length; i++) {
L->base[i - 1] = L->base[i];
}
*e = L->base[position - 1];
L->length--;
return OK;
}
Status SqlDestroy(Sqlist *L) {
if (!L->base)
return ERROR;
else {
free(L->base);
return OK;
}
}
void SqlClear(Sqlist *L) { L->length = 0; }
Status SqlIsEmpty(Sqlist *L) {
if (0 == L->length)
return TRUE;
else
return FALSE;
}9、顺序表的完整测试文件
1)、SequenceList.h
c
#include <stdio.h>
#include <stdlib.h>
#ifndef __SEQUENCELIST_H
#define __SEQUENCELIST_H
//函数返回状态
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
//顺序表所需结构定义
#define SQLMAXSIZE 100 //顺序表存储空间大小
typedef int SqlElemType; //顺序表存储内容
typedef struct __Sqlist { //顺序表结构
SqlElemType *base;
int length; //当前表大小;
} Sqlist;
//初始化顺序表
Status InitSL(Sqlist *L, int length);
//获取顺序表元素
Status GetElem(Sqlist *L, int position, SqlElemType *e);
//查找顺序表元素
int LocateElem(Sqlist *L, SqlElemType e);
//顺序表插入新元素
Status SqlInsert(Sqlist *L, int position, SqlElemType e);
//删除元素
Status SqlDelete(Sqlist *L, int position, SqlElemType *e);
//销毁顺序表
Status SqlDestroy(Sqlist *L);
//清空顺序表
void SqlClear(Sqlist *L);
//检查顺序表是否为空
Status SqlIsEmpty(Sqlist *L);
//合并两个顺序表
void MergeList(Sqlist *La, Sqlist *Lb);
//遍历打印顺序表
void Traverse(Sqlist *L);
//有序表合并
void MergeList_Seq(Sqlist *La, Sqlist *Lb, Sqlist *Lc);
#endif2)、SequenceList.c
c
#include "SequenceList.h"
Status InitSL(Sqlist *L, int length)
{
L->base = (SqlElemType *)malloc(sizeof(SqlElemType) * SQLMAXSIZE);
if (!L->base)
return OVERFLOW;
L->length = 0;
for (int i = 1; i < length + 1; i++)
{
SqlElemType e;
scanf(" %d", &e);
SqlInsert(L, i, e);
}
return OK;
}
Status GetElem(Sqlist *L, int position, SqlElemType *e)
{
if (position < 1 || position > L->length)
return ERROR;
*e = L->base[position - 1];
return OK;
}
//
int LocateElem(Sqlist *L, SqlElemType e)
{
for (int i = 0; i < L->length; i++)
{
if (e == L->base[i])
return i + 1;
}
return 0; // 0代表查找元素不在循序表中
}
Status SqlInsert(Sqlist *L, int position, SqlElemType e)
{
if (position < 1 || position > L->length + 1)
return ERROR;
if (L->length == SQLMAXSIZE)
return OVERFLOW;
for (int i = L->length - 1; i >= position - 1; i--)
{ // 注意需要把数组中的元素全部向右移动,需要从数组最右边的元素开始移动
L->base[i + 1] = L->base[i];
}
L->base[position - 1] = e;
L->length++;
return OK;
}
Status SqlDelete(Sqlist *L, int position, SqlElemType *e)
{
if (position < 1 || position > L->length)
return ERROR;
for (int i = position; i < L->length; i++)
{
L->base[i - 1] = L->base[i];
}
*e = L->base[position - 1];
L->length--;
return OK;
}
Status SqlDestroy(Sqlist *L)
{
if (!L->base)
return ERROR;
else
{
free(L->base);
return OK;
}
}
void SqlClear(Sqlist *L)
{
L->length = 0;
}
Status SqlIsEmpty(Sqlist *L)
{
if (0 == L->length)
return TRUE;
else
return FALSE;
}
void MergeList(Sqlist *La, Sqlist *Lb)
{
for (int i = 1; i < Lb->length + 1; i++)
{
SqlElemType e;
GetElem(Lb, i, &e);
if (!LocateElem(La, e))
{
La->base[La->length++] = e;
}
}
}
void Traverse(Sqlist *L)
{
for (int i = 0; i < L->length; i++)
{
printf("%d ", L->base[i]);
}
}
void MergeList_Seq(Sqlist *La, Sqlist *Lb, Sqlist *Lc)
{
Lc->length = La->length + Lb->length;
SqlElemType *pa = La->base, *pa_last = pa + La->length - 1;
// pa指向La->base的首地址,pa_last指向base中最后一个元素的地址,下面同理
SqlElemType *pb = Lb->base, *pb_last = pb + Lb->length - 1;
SqlElemType *pc = Lc->base;
while (pa <= pa_last && pb <= pb_last)
{
// 当pa>pa_last时说明,有集合中的元素已经全部加入到Lc中
if (*pa < *pb)
*(pc++) = *(pa++);
else
*(pc++) = *(pb++);
}
while (pa <= pa_last)
*(pc++) = *(pa++); // 判断La的元素是否全部加入Lc中,下面同理
while (pb <= pb_last)
*(pc++) = *(pb++);
}3)、main.c
c
#include "SequenceList.h"
int main(void)
{
Sqlist L;
printf("------构造一个空的线性表L------\n");
InitSL(&L, 0);
Traverse(&L); //打印结果
printf("------测试插入10个数------\n");
for(int i = 1;i <= 10; i++){
SqlInsert(&L,i,i);
}
Traverse(&L); //打印结果
printf("------在第三位之前插入0------\n");
SqlInsert(&L,3,0);
Traverse(&L); //打印结果
printf("------删除第6位的数据------\n");
SqlElemType e;
SqlDelete(&L,6,&e);
printf("删除的数据为:%d\n", e);
Traverse(&L); //打印结果
printf("------获取元素操作------\n");
GetElem(&L,5,&e);
printf("得到第5个元素:%d\n", e);
system("pause");
return 0;
}4)、运行结果
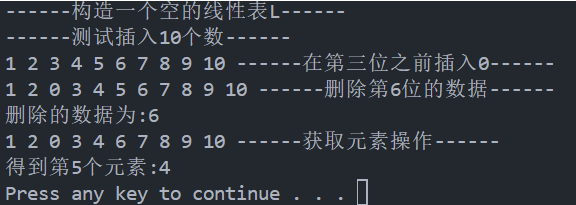
三、单链表(Single Linked List)
1、单链表
单链表由头节点(不存放数据只存放下个节点的地址)和n个节点组成。
用一组物理位置任意的存储单元来存放线性表的数据元素。
这组存储单元即可以是连续的,也可以是不连续的,甚至是零散分布在内存中的任意位置上。
链表中元素的逻辑次序和物理次序不一定相同。
每个节点分为两个域:数据域和指针域(存放下个节点的地址)。
第n个节点的指针域为NULL。
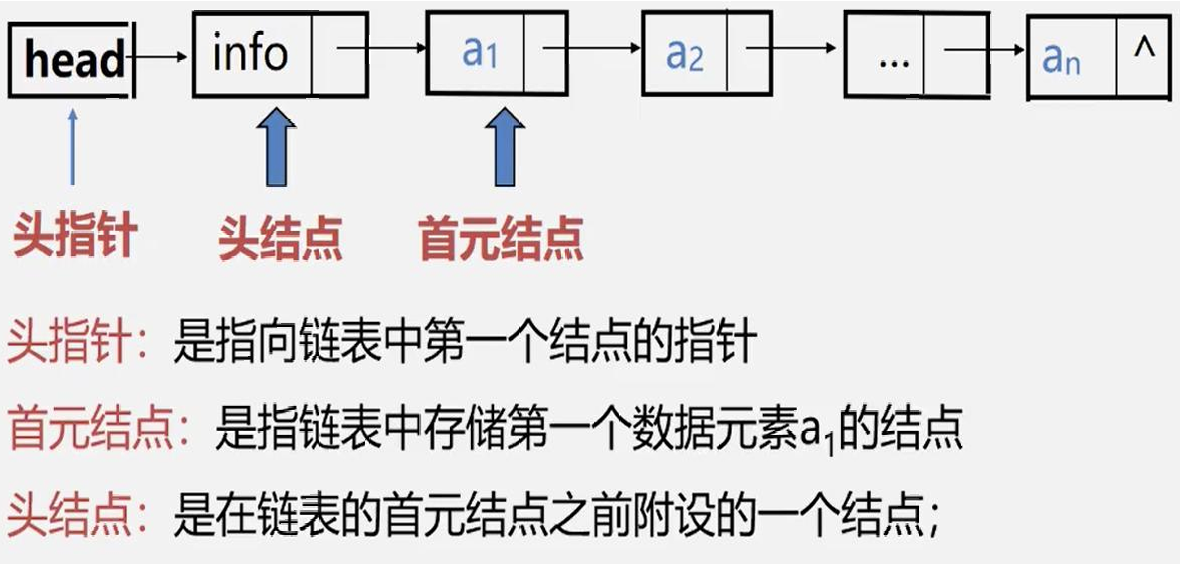
c
typedef int LlElemtype;
typedef struct __LNode {
LlElemtype data; //存放单个节点的数据
__LNode *next; //存放下个节点的地址
} LNode, *LinkList;2、初始化
c
Status InitLL(LinkList *L) // L是个二级指针
{
(*L) = (LinkList)malloc(sizeof(LNode));
(*L)->next = NULL;
return OK;
}3、创建链表(头插法)
c
void CreatLL_H(LinkList L, int n)
//用此方法创建的链表,遍历的顺序和创建的顺序相反
{
printf("Please input %d numbers:", n);
for (int i = 0; i < n; i++) {
LinkList p = (LinkList)malloc(sizeof(LNode));
int data;
scanf(" %d", &data); //%d前面的空格代表清除制表符回车等符号
p->data = data;
p->next = L->next;
L->next = p;
}
}4、创建链表(尾插法)
c
void CreatLL_R(LinkList L, int n) {
printf("Please input %d numbers:", n);
LinkList ptail;
ptail = L;
for (int i = 0; i < n; i++) {
LinkList pnew;
pnew = (LinkList)malloc(sizeof(LNode));
int data;
scanf(" %d", &data);
pnew->data = data;
pnew->next = NULL;
ptail->next = pnew;
ptail = pnew;
}
}5、获取元素
c
Status GetElem(LinkList L, int position, LlElemtype *e) {
LinkList p = L->next;
int i = 1; //使i和p的位置同步,即i代表着p在链表中的位置
if (position < 1 || !p)
return ERROR;
while (p && i < position) { //此处不可 i<=position,因为while成立时,内部会i++
p = p->next;
i++;
}
*e = p->data;
return OK;
}6、查找元素
c
LinkList LocateElem(LinkList L, LlElemtype e) {
LinkList p = L->next;
while (p && p->data != e) {
p = p->next;
}
if (!p)
return NULL; //如果p的地址为空 说明e不在链表中
return p;
}7、插入元素
想在a,b之间插入 ,需要先知道a节点的地址.
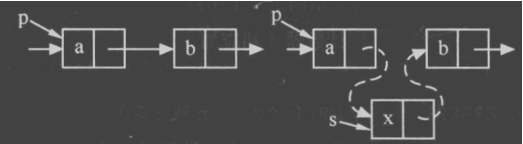
如果想要在位置 i 插入节点,则需要知道位置 i-1 节点的位置。
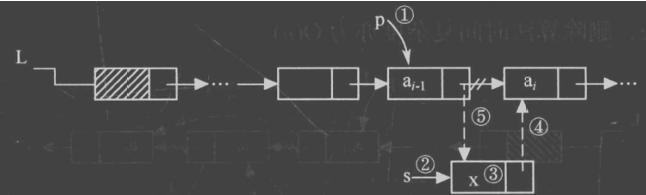
注意因为插入操作和GetElem操作不同。
要从0开始,p要从L开始。
如果从1和L开始的话,无法再位置1插入元素。
c
Status LlInsert(LinkList L, int position, LlElemtype e) {
LinkList p = L; //注意因为插入操作和GetElem操作不同
int i = 0;
// i要从0开始,p要从L开始
//如果从1和L开始的话,无法再位置1插入元素
while (p && i < position - 1) { //查找插入节点位置的前一个节点
i++;
p = p->next;
}
if (!p || i > position - 1)
return ERROR;
LinkList pnew = (LinkList)malloc(sizeof(LNode));
pnew->data = e;
pnew->next = p->next;
p->next = pnew;
return OK;
}8、删除元素
想要删除,则必须先知道的地址。
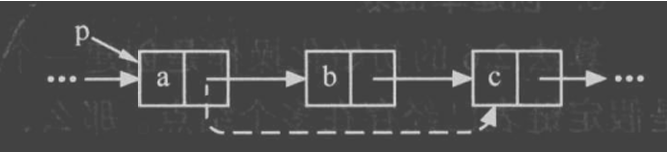
注意因为插入操作和GetElem操作不同。
要从0开始,p要从L开始。
如果从1和L开始的话,无法再位置1插入元素。
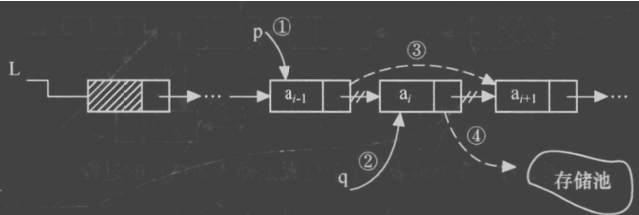
c
Status LlDelete(LinkList L, int position, LlElemtype *e) {
LinkList p = L;
int i = 0;
while (p && i < position - 1) {
//查找posision-1位置节点的地址
i++;
p = p->next;
}
if (i > position - 1 || !p || !p->next)
return ERROR;
//注意是 多增加了判断条件!(p->next) 当节点数为n,删除的位置为n+1时会返回error
LinkList pfree = p->next;
*e = pfree->data;
p->next = pfree->next; //此处可改写成 p->next = p->next->next;
free(pfree);
return OK;
}9、总结插入和删除操作算法的不同
c
while (p){
p = p->next;
}//最终p的值为NULL
while(p->next){
p = p->next;
}//最终p的值为最后一个节点的地址
//---------------------插入----------------------
//如果插入操作的position不合法,即position > n+1(n为链表长度),那么p一定会指向NULL,此时按照退出条件!p可以返回ERROR
if (!p || i>position-1) return ERROR;
//但是如果采用:
while(p->next)
//则最终会指向链表最后一个节点,即使position不合法,那么也会在最后一个节点后方插入新节点
//所以使用:
while(p)
////---------------------删除----------------------
//如果删除操作的positoin不合法,即position>链表长度,p会指向,最后一个节点的地址(position == n+1时)或是NULL(position > n+1),那么下面的代码会出错。
LinkList pfree = p->next;
//如果p指向最后一个节点,此时pfree指向NULL。如果p指向NULL,此时pfree指向非法空间(不受主程序控制),从而导致下面代码报错
*e = pfree->data;
//所以需要增加一个判断条件
if (i>position-1 || !p || !p->next) return ERROR;
//必须保证 !p 要在 !p->next的左边,即position > n+1 的情况
//这是因为如果 !p->next 在 !p 的左边,如果p指向NULL,那么NULL->next会报错10、销毁链表
c
Status LlDestroy(LinkList *L) {
if (!(*L))
return ERROR;
LinkList p = *L;
while (p) {
LinkList pfree = p; // pfree保存要释放的节点地址
p = p->next;
//此行和下行的顺序不能反
free(pfree);
pfree = NULL;
}
*L = NULL;
return OK;
}11、单链表测试文件
1)、SingleLinkedList.h
c
#include <stdio.h>
#include <stdlib.h>
#ifndef __LINKLIST_H
#define __LINKLIST_H
//函数返回状态
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int LlElemtype;
typedef struct __LNode
{
LlElemtype data; // 存放单个节点的数据
struct __LNode *next; // 存放下个节点的地址
} LNode, *LinkList;
//初始化单链表
Status InitLL(LinkList *L);
//创建链表(头插法)
void CreatLL_H(LinkList L, int n);
//创建链表(尾插法)
void CreatLL_R(LinkList L, int n);
//获取元素
Status GetElem(LinkList L, int position, LlElemtype *e);
//查找元素
LinkList LocateElem(LinkList L, LlElemtype e);
//插入元素
Status LlInsert(LinkList L, int position, LlElemtype e);
//删除元素
Status LlDelete(LinkList L, int position, LlElemtype *e);
//遍历打印单链表
void Traverse(LinkList *L);
//清空单链表
Status LlDestroy(LinkList *L);
//合并单链表
void Merge_LinkedList(LinkList *La, LinkList *Lb, LinkList *Lc);
#endif2)、SingleLinkedList.c
c
#include "SingleLinkedList.h"
Status InitLL(LinkList *L) // L是个二级指针
{
(*L) = (LinkList)malloc(sizeof(LNode));
(*L)->next = NULL;
return OK;
}
void CreatLL_H(LinkList L, int n)
// 用此方法创建的链表,遍历的顺序和创建的顺序相反
{
printf("Please input %d numbers:", n);
for (int i = 0; i < n; i++)
{
LinkList p = (LinkList)malloc(sizeof(LNode));
int data;
scanf("%d", &data); //%d前面的空格代表清除制表符回车等符号
p->data = data;
p->next = L->next;
L->next = p;
}
}
void CreatLL_R(LinkList L, int n)
{
printf("Please input %d numbers:", n);
LinkList ptail;
ptail = L;
for (int i = 0; i < n; i++)
{
LinkList pnew;
pnew = (LinkList)malloc(sizeof(LNode));
int data;
scanf(" %d", &data);
pnew->data = data;
pnew->next = NULL;
ptail->next = pnew;
ptail = pnew;
}
}
Status GetElem(LinkList L, int position, LlElemtype *e)
{
LinkList p = L->next;
int i = 1; // 使i和p的位置同步,即i代表着p在链表中的位置
if (position < 1 || !p)
return ERROR;
while (p && i < position)
{ // 此处不可 i<=position,因为while成立时,内部会i++
p = p->next;
i++;
}
*e = p->data;
return OK;
}
LinkList LocateElem(LinkList L, LlElemtype e)
{
LinkList p = L->next;
while (p && p->data != e)
{
p = p->next;
}
if (!p)
return NULL; // 如果p的地址为空 说明e不在链表中
return p;
}
Status LlInsert(LinkList L, int position, LlElemtype e)
{
LinkList p = L; // 注意因为插入操作和GetElem操作不同
int i = 0;
// i要从0开始,p要从L开始
// 如果从1和L开始的话,无法再位置1插入元素
while (p && i < position - 1)
{ // 查找插入节点位置的前一个节点
i++;
p = p->next;
}
if (!p || i > position - 1)
return ERROR;
LinkList pnew = (LinkList)malloc(sizeof(LNode));
pnew->data = e;
pnew->next = p->next;
p->next = pnew;
return OK;
}
Status LlDelete(LinkList L, int position, LlElemtype *e)
{
LinkList p = L;
int i = 0;
while (p && i < position - 1)
{
// 查找posision-1位置节点的地址
i++;
p = p->next;
}
if (i > position - 1 || !p || !p->next)
return ERROR;
// 注意是 多增加了判断条件!(p->next) 当节点数为n,删除的位置为n+1时会返回error
LinkList pfree = p->next;
*e = pfree->data;
p->next = pfree->next; // 此处可改写成 p->next = p->next->next;
free(pfree);
return OK;
}
void Traverse(LinkList *L)
{
if (!(*L))
{
printf("链表为空!");
return;
}
LinkList p = (*L)->next;
while (p)
{
printf("%d ", p->data);
p = p->next;
}
printf("\n");
}
Status LlDestroy(LinkList *L)
{
if (!(*L))
return ERROR;
LinkList p = *L;
while (p)
{
LinkList pfree = p; // pfree保存要释放的节点地址
p = p->next;
// 此行和下行的顺序不能反
free(pfree);
pfree = NULL;
}
*L = NULL;
return OK;
}
void Merge_LinkedList(LinkList *La, LinkList *Lb, LinkList *Lc)
{
*Lc = *La; // 让Lc使用La的头节点进行合并
LinkList pa = (*La)->next, pb = (*Lb)->next; // pa, pb分别表示合并时所指节点
LinkList pc = *Lc; // pc表示Lc的尾节点
while (pa && pb)
{
if (pa->data < pb->data)
{
pc->next = pa;
pc = pa;
pa = pa->next;
}
else
{
pc->next = pb;
pc = pb;
pb = pb->next;
}
}
pc->next = pa ? pa : pb;
// pc->next不需要NULL,因为合并时一定会剩下一串节点,只需指向该剩下的节点就OK
free(*Lb);
*La = *Lb = NULL;
}3)、main.c
c
#include "SingleLinkedList.h"
int main()
{
LinkList L;
//构造单链表
InitLL(&L);
printf("------测试插入10个数------\n");
for(int i = 1; i<=10;i++){
LlInsert(L,i,i);
}
Traverse(&L);
printf("------删除第5位的数据------\n");
LlElemtype elem;
LlDelete(L,5,&elem);
Traverse(&L);
printf("------清空单链表------\n");
LlDestroy(&L);
Traverse(&L);
}4)、运行结果

四、循环链表(Circular Linked List)
循环链表的特点:
最后一个节点的指针域指向头节点,整个表链形成一个环。
由此,从表中任意节点出发,可以找到其他节点。

和单链表很像,区别就是最后一个节点的next域指向头节点。
五、双向链表(Double Linked List)
有两个指针域,一个指向直接前驱,另一个指向直接后继。

1、数据类型
c
typedef int DouLElemtype;
typedef struct __DouLinkNode {
DouLElemtype data;
__DouLinkNode *prior;
__DouLinkNode *next;
} DouLinkNode, *DouLinkList;2、初始化
c
void InitDL(DouLinkList *L) {
*L = (DouLinkList)malloc(sizeof(DouLinkNode));
(*L)->next = NULL;
(*L)->prior = NULL;
}3、创建双向链表
c
void CreatDL_H(DouLinkList L, int length) {
for (int i = 0; i < length; i++) {
DouLinkList pnew = (DouLinkList)malloc(sizeof(DouLinkNode));
int data;
printf("(for %d)Please input the data:", i + 1);
scanf("%d", &data);
pnew->data = data;
pnew->next = L->next;
pnew->prior = L;
L->next = pnew;
}
}
void CreatDL_R(DouLinkList L, int length) {
DouLinkList ptail = L;
for (int i = 0; i < length; i++) {
DouLinkList pnew = (DouLinkList)malloc(sizeof(DouLinkNode));
int data;
printf("(for %d)Please input the data:", i + 1);
scanf("%d", &data);
pnew->data = data;
pnew->next = NULL;
pnew->prior = ptail;
ptail->next = pnew;
ptail = pnew;
}
}4、插入和删除
c
void DlInsert(DouLinkList L, int position, DouLElemtype e) {
int i = 0;
DouLinkList p = L;
while (p->next && i < position - 1) {
i++;
p = p->next;
}
DouLinkList pnew = (DouLinkList)malloc(sizeof(DouLinkNode));
pnew->data = e;
pnew->next = p->next;
pnew->prior = p;
p->next = pnew;
p->next->prior = pnew;
}
void DlDelete(DouLinkList L, int position, DouLElemtype *e) {
DouLinkList p = L;
int i = 0;
while (p->next && i < position - 1) {
p = p->next;
i++;
}
DouLinkList pfree = p->next;
*e = pfree->data;
p->next = p->next->next;
p->next->next->prior = p;
free(pfree);
pfree = NULL;
}5、双向链表测试文件
1)、DoubleLinkedList.h
c
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>
#ifndef __DOUBLELINKEDLIST_H
#define __DOUBLELINKEDLIST_H
//函数返回状态
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int DouLElemtype;
typedef struct __DouLinkNode
{
struct __DouLinkNode* prior;
struct __DouLinkNode* next;
DouLElemtype data;
}DouLinkNode, *DouLinkList;
//初始化
void InitDL(DouLinkList *L);
//创建双向链表
void CreatDL_H(DouLinkList L, int length) ;
void CreatDL_R(DouLinkList L, int length) ;
//插入
void DlInsert(DouLinkList L, int position, DouLElemtype e);
//删除
void DlDelete(DouLinkList L, int position, DouLElemtype *e);
//获取元素
Status GetElem(DouLinkList L, int position, DouLElemtype *e);
//查找元素
DouLinkList LocateElem(DouLinkList L, DouLElemtype e);
//清空双向链表
Status DlDestroy(DouLinkList *L);
//遍历打印双向链表
void Traverse(DouLinkList *L);
#endif2)、DoubleLinkedList.c
c
#include "DoubleLinkedList.h"
void InitDL(DouLinkList *L)
{
*L = (DouLinkList)malloc(sizeof(DouLinkNode));
(*L)->next = NULL;
(*L)->prior = NULL;
}
void CreatDL_H(DouLinkList L, int length)
{
for (int i = 0; i < length; i++)
{
DouLinkList pnew = (DouLinkList)malloc(sizeof(DouLinkNode));
int data;
printf("(for %d)Please input the data:", i + 1);
scanf("%d", &data);
pnew->data = data;
pnew->next = L->next;
pnew->prior = L;
L->next = pnew;
}
}
void CreatDL_R(DouLinkList L, int length)
{
DouLinkList ptail = L;
for (int i = 0; i < length; i++)
{
DouLinkList pnew = (DouLinkList)malloc(sizeof(DouLinkNode));
int data;
printf("(for %d)Please input the data:", i + 1);
scanf("%d", &data);
pnew->data = data;
pnew->next = NULL;
pnew->prior = ptail;
ptail->next = pnew;
ptail = pnew;
}
}
void DlInsert(DouLinkList L, int position, DouLElemtype e)
{
int i = 0;
DouLinkList p = L;
while (p->next && i < position - 1)
{
i++;
p = p->next;
}
DouLinkList pnew = (DouLinkList)malloc(sizeof(DouLinkNode));
pnew->data = e;
pnew->next = p->next;
pnew->prior = p;
p->next = pnew;
p->next->prior = pnew;
}
void DlDelete(DouLinkList L, int position, DouLElemtype *e)
{
DouLinkList p = L;
int i = 0;
while (p->next && i < position - 1)
{
p = p->next;
i++;
}
DouLinkList pfree = p->next;
*e = pfree->data;
p->next = p->next->next;
p->next->next->prior = p;
free(pfree);
pfree = NULL;
}
//获取元素
Status GetElem(DouLinkList L, int position, DouLElemtype *e)
{
DouLinkList p = L->next;
int i = 0;
if (position < 1 || !p)
return ERROR;
while (p->next && i < position - 1)
{
i++;
p = p->next;
}
*e = p->data;
return OK;
}
//查找元素
DouLinkList LocateElem(DouLinkList L, DouLElemtype e)
{
DouLinkList p = L->next;
while (p && p->data != e)
{
p = p->next;
}
if (!p)
return NULL; // 如果p的地址为空 说明e不在链表中
return p;
}
//清空双向链表
Status DlDestroy(DouLinkList *L)
{
if (!(L))
return ERROR;
DouLinkList p = *L;
while (p)
{
DouLinkList pfree = p; // pfree保存要释放的节点地址
p = p->next;
// 此行和下行的顺序不能反
free(pfree);
pfree = NULL;
}
*L = NULL;
return OK;
}
//遍历打印双向链表
void Traverse(DouLinkList *L)
{
if (!(*L))
{
printf("链表为空!");
return;
}
DouLinkList p = (*L)->next;
while (p)
{
printf("%d ", p->data);
p = p->next;
}
printf("\n");
}3)、main.c
c
#include "DoubleLinkedList.h"
int main()
{
DouLinkList L;
//构造双向链表
InitDL(&L);
printf("------测试插入10个数------\n");
for(int i = 1; i<=10;i++){
DlInsert(L,i,i);
}
Traverse(&L);
printf("------删除第5位的数据------\n");
DouLElemtype elem;
DlDelete(L,5,&elem);
Traverse(&L);
printf("------清空单链表------\n");
DlDestroy(&L);
Traverse(&L);
return 0;
}4)、运行结果
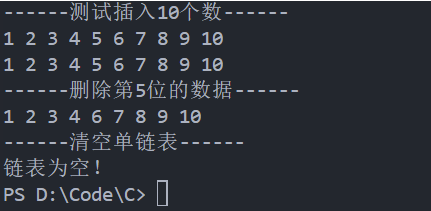
六、线性表其它操作
1、线性表合并
已知两个集合
求出合并后集合
c
void MergeList(Sqlist *La, Sqlist *Lb) {
for (int i = 1; i < Lb->length + 1; i++) {
SqlElemType e;
GetElem(Lb, i, &e);
if (!LocateElem(La, e)) {
La->base[La->length++] = e;
}
}
}
void Traverse(Sqlist *L) {
for (int i = 0; i < L->length; i++) {
printf("%d ", L->base[i]);
}
}
主程序
#include <SequenceList.h>
int main(void) {
Sqlist La, Lb;
Sqlist *pa = &La;
Sqlist *pb = &Lb;
InitSL(pa, 4);
InitSL(pb, 3);
MergeList(pa, pb);
Traverse(pa);
system("pause");
return 0;
}
/*
7 5 3 11
2 6 3
*/2、有序表合并(并归排序的基础)
c
void MergeList_Seq(Sqlist *La, Sqlist *Lb, Sqlist *Lc) {
Lc->length = La->length + Lb->length;
SqlElemType *pa = La->base, *pa_last = pa + La->length - 1;
// pa指向La->base的首地址,pa_last指向base中最后一个元素的地址,下面同理
SqlElemType *pb = Lb->base, *pb_last = pb + Lb->length - 1;
SqlElemType *pc = Lc->base;
while (pa <= pa_last && pb <= pb_last) {
//当pa>pa_last时说明,有集合中的元素已经全部加入到Lc中
if (*pa < *pb)
*(pc++) = *(pa++);
else
*(pc++) = *(pb++);
}
while (pa <= pa_last)
*(pc++) = *(pa++); //判断La的元素是否全部加入Lc中,下面同理
while (pb <= pb_last)
*(pc++) = *(pb++);
}
主程序
#include <SequenceList.h>
int main(void) {
Sqlist La, Lb, Lc;
InitSL(&La, 4);
InitSL(&Lb, 7);
InitSL(&Lc, 0);
MergeList_Seq(&La, &Lb, &Lc);
Traverse(&Lc);
system("pause");
return 0;
}
/*
3 5 8 11
2 6 8 9 11 15 20
*/3、有序链表合并
c
void Merge_LinkedList(LinkList *La, LinkList *Lb, LinkList *Lc) {
*Lc = *La; //让Lc使用La的头节点进行合并
LinkList pa = (*La)->next, pb = (*Lb)->next; // pa, pb分别表示合并时所指节点
LinkList pc = *Lc; // pc表示Lc的尾节点
while (pa && pb) {
if (pa->data < pb->data) {
pc->next = pa;
pc = pa;
pa = pa->next;
} else {
pc->next = pb;
pc = pb;
pb = pb->next;
}
}
pc->next = pa ? pa : pb;
// pc->next不需要NULL,因为合并时一定会剩下一串节点,只需指向该剩下的节点就OK
free(*Lb);
*La = *Lb = NULL;
}
主程序
#include "LinkList.h"
int main(void) {
LinkList La, Lb, Lc;
InitLL(&La), InitLL(&Lb), InitLL(&Lc);
CreatLL_R(La, 4);
CreatLL_R(Lb, 7);
Merge_LinkedList(&La, &Lb, &Lc);
Traverse(Lc);
system("pause");
return 0;
}
/*
3 5 8 11
2 6 8 9 11 15 20
*/4、多项式创建 and 多项式相加
创建一个多项式,并按照指数的高低排序
多项式结构体
c
typedef struct __PolyNode {
double coeffcient;
int exponent;
__PolyNode *next;
} PolyNode, *Polynomial; 多项式创建
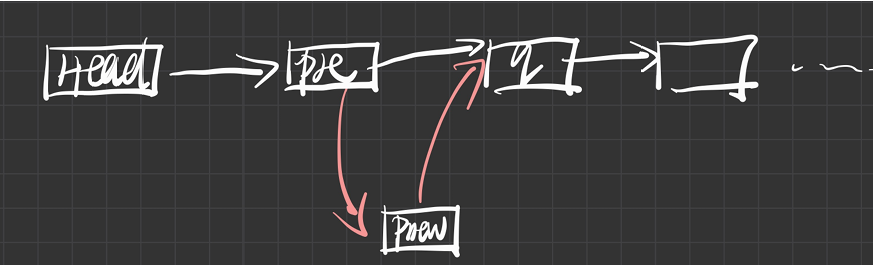
核心变量为 :
Polynomial q; Polynimial pre;
核心语句为 :
while(q && q->exponent < pnew->exponent)
c
void InitPolynomial(Polynomial *p, int length) {
*p = (Polynomial)malloc(sizeof(PolyNode)); //先初始化头节点
(*p)->next = NULL;
printf("Please input the coefficient and exponent:");
for (int i = 0; i < length; i++) {
Polynomial pnew = (Polynomial)malloc(sizeof(PolyNode));
scanf(" %lf", &(pnew->coeffcient));
scanf(" %d", &(pnew->exponent));
Polynomial q = (*p)->next; // q为指向比pew->exponent大的节点
Polynomial pre = (*p);
// pre指向q的直接前驱节点
}
}
while (q && q->exponent < pnew->exponent) { //第1次的for循环不会执行
//直到找到一个节点的exponent大于pnew->exponent,如果没找到q指向NULL
pre = q;
q = q->next;
}
pnew->next = q; //因为q->exponent > pnew->exponent
pre->next = pnew;
}
主程序
#include <stdio.h>
#include <stdlib.h>
typedef struct __PolyNode {
double coeffcient;
int exponent;
__PolyNode *next;
} PolyNode, *Polynomial;
void InitPolynomial(Polynomial *p, int length);
void Traverse(Polynomial P);
Polynomial AddPolynomial(Polynomial pa, Polynomial pb);
int main(void) {
Polynomial p1, p2, p3;
InitPolynomial(&p1, 3);
InitPolynomial(&p2, 4);
p3 = AddPolynomial(p1, p2);
Traverse(p1);
No. 19 / 99
system("pause");
return 0;
}
/*
x^6+2x^2+3x^5-2x^2+3x^5+2x^6+x^3--------------------------
intput:
1 6 2 2 3 5-2 2 3 5 2 6 1 3----------------------------
output:
(1.0x^3)+(6.0x^5)+(3.0x^6)
*/