使用稀疏采样方法减轻汽车雷达干扰
J. Bechter, F. Roos, M. Rahman and C. Waldschmidt, "Automotive radar interference mitigation using a sparse sampling approach," 2017 European Radar Conference (EURAD), Nuremberg, Germany, 2017, pp. 90-93
论文:使用稀疏采样方法的汽车雷达干扰抑制
引言与问题背景
随着高级驾驶辅助系统 (ADAS) 和自动驾驶技术的不断发展,雷达传感器已经成为不可或缺的组件。它们在雾天、雨天等恶劣天气条件下的可靠功能是其他传感器(如摄像头)无法比拟的。然而,道路上雷达传感器的数量急剧增加,也导致传感器之间相互干扰的概率显著上升。这种干扰会严重降低传感器的检测能力,在最坏的情况下甚至可能导致传感器"失明",无法检测到目标。
对于汽车领域非常常见的 FMCW(调频连续波)雷达,当传感器具有不同的调频斜率时,极有可能发生干扰。虽然这种干扰产生"幽灵目标"的概率很低,但它会在基带信号中引入宽带噪声,显著提高本底噪声,从而严重降低传感器的检测性能。在时域上,FMCW 雷达的干扰通常表现为具有非常高幅度且时间受限的伪影。检测这些干扰的方法有很多,例如功率检测器、匹配滤波器,甚至图像处理技术。在检测到干扰后,一种被广泛采用的缓解措施是简单地移除(置零)受到干扰的信号采样点。这种方法虽然能消除干扰引入的噪声基底,但它在时域信号中引入了一个"缺口"(gap)。这个缺口会在频域中产生新的伪影,从而带来新的问题。
本文的核心工作是解决这个"缺口"问题。作者没有止步于简单置零,而是提出应用一种源于压缩感知的稀疏采样信号恢复算法,对丢失样本进行重建。
干扰场景与问题描述
为分析"缺口"问题,论文构建了一个贴近实际的道路场景,如图 1 所示。
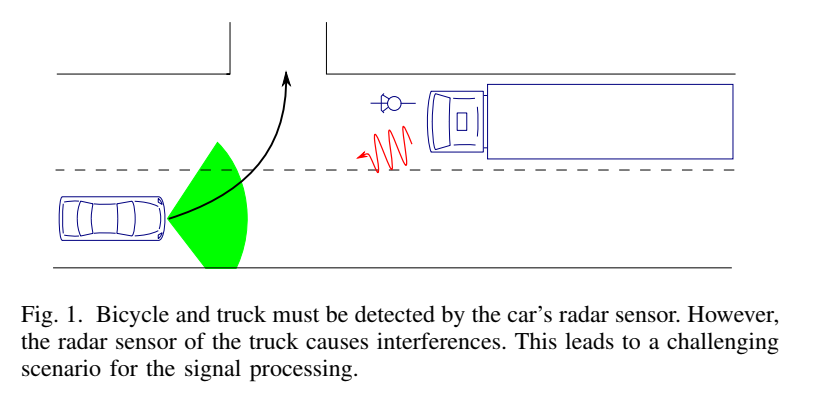
在该场景中,一辆搭载雷达的汽车正准备左转,需可靠检测对向车道驶来的卡车与自行车。卡车无法超车,因此与自行车保持相同的 5 m/s 速度。
场景与雷达参数:
-
汽车雷达 (Car): 带宽 B=500 MHzB=500~\text{MHz}B=500 MHz,斜坡持续时间 T=45 μsT=45~\mu sT=45 μs
-
卡车雷达 (Truck): 带宽 B=700 MHzB=700~\text{MHz}B=700 MHz,斜坡持续时间 T=45 μsT=45~\mu sT=45 μs
-
目标详情:
- 卡车:RCS =20 dBsm=20~\text{dBsm}=20 dBsm(强目标),距离 =19 m=19~\text{m}=19 m
- 自行车:RCS =−10 dBsm=-10~\text{dBsm}=−10 dBsm(弱目标),距离 =15 m=15~\text{m}=15 m
在没有干扰的情况下,汽车雷达本可以轻松检测到这两个目标。
干扰的数学分析与"缺口"问题
问题的关键在于:卡车雷达的调制参数与汽车雷达不同,二者的调频斜率 (B/T)(B/T)(B/T) 不同。根据 FMCW 干扰理论,这种斜率差会导致一个持续时间为 TIntT_{\mathrm{Int}}TInt 的干扰信号,该信号会扫过汽车雷达接收机带宽 BRxB_{\mathrm{Rx}}BRx(本文设为 4.4 MHz4.4~\text{MHz}4.4 MHz)。
干扰持续时间 TIntT_{\mathrm{Int}}TInt 为:
TInt=2BRx∣BTruckTTruck−BCarTCar∣=2×4.4 MHz∣700 MHz45 μs−500 MHz45 μs∣≈2 μs. T_{\mathrm{Int}} =\frac{2B_{\mathrm{Rx}}}{\left|\frac{B_{\mathrm{Truck}}}{T_{\mathrm{Truck}}}-\frac{B_{\mathrm{Car}}}{T_{\mathrm{Car}}}\right|} =\frac{2\times 4.4~\text{MHz}}{\left|\frac{700~\text{MHz}}{45~\mu s}-\frac{500~\text{MHz}}{45~\mu s}\right|} \approx 2~\mu s . TInt= TTruckBTruck−TCarBCar 2BRx= 45 μs700 MHz−45 μs500 MHz 2×4.4 MHz≈2 μs.
在采样率 fs=10 MHzf_s=10~\text{MHz}fs=10 MHz 下,这 2 μs2~\mu s2 μs 的干扰会污染一帧(T=45 μsT=45~\mu sT=45 μs)内 450450450 个总采样点中的 202020 个(2 μs×10 MHz=202~\mu s \times 10~\text{MHz}=202 μs×10 MHz=20)。
将这 20 个受干扰样本置零以抑制干扰,会在时域中人为引入一个持续时间为 TIntT_{\mathrm{Int}}TInt 的缺口。设一个幅度 A0A_0A0、频率 f0f_0f0 的纯净分量(代表一个目标)可建模为:
s(t)=A0cos(2πf0t)⋅[rect (tT)−rect (tTInt)]. s(t)=A_0\cos(2\pi f_0 t)\cdot\Bigl[\operatorname{rect}\!\Bigl(\tfrac{t}{T}\Bigr)-\operatorname{rect}\!\Bigl(\tfrac{t}{T_{\mathrm{Int}}}\Bigr)\Bigr]. s(t)=A0cos(2πf0t)⋅[rect(Tt)−rect(TIntt)].
这表示:原本完整的矩形时间窗 rect(t/T)\operatorname{rect}(t/T)rect(t/T) 被挖去一个表示"缺口"的小矩形窗 rect(t/TInt)\operatorname{rect}(t/T_{\mathrm{Int}})rect(t/TInt)。
在频域,从 s(t)s(t)s(t) 的傅里叶变换得到频谱 S(f)S(f)S(f)(下式仅写正频部分的贡献):
S(f)=A02 δ(f−f0)∗[T⋅si(πTf)−TInt⋅si(πTIntf)], S(f)=\frac{A_0}{2}\,\delta(f-f_0)\ast\bigl[T\cdot \mathrm{si}(\pi T f)-T_{\mathrm{Int}}\cdot \mathrm{si}(\pi T_{\mathrm{Int}} f)\bigr], S(f)=2A0δ(f−f0)∗[T⋅si(πTf)−TInt⋅si(πTIntf)],
其中 si(x)=sin(x)/x\mathrm{si}(x)=\sin(x)/xsi(x)=sin(x)/x。含义是:原本尖锐的 δ(f−f0)\delta(f-f_0)δ(f−f0) 需与两个 si\mathrm{si}si(sinc 型)函数卷积:
- T⋅si(πTf)T\cdot \mathrm{si}(\pi T f)T⋅si(πTf):由整段时间窗产生,主瓣窄、旁瓣低;
- −TInt⋅si(πTIntf)-T_{\mathrm{Int}}\cdot \mathrm{si}(\pi T_{\mathrm{Int}} f)−TInt⋅si(πTIntf):由"缺口"产生。由于 TInt≪TT_{\mathrm{Int}}\ll TTInt≪T,其主瓣很宽、旁瓣密而高。
两者叠加使强目标能量通过宽旁瓣扩散,产生显著伪影,淹没邻近的弱目标。
图 2 直观展示了以上效应。
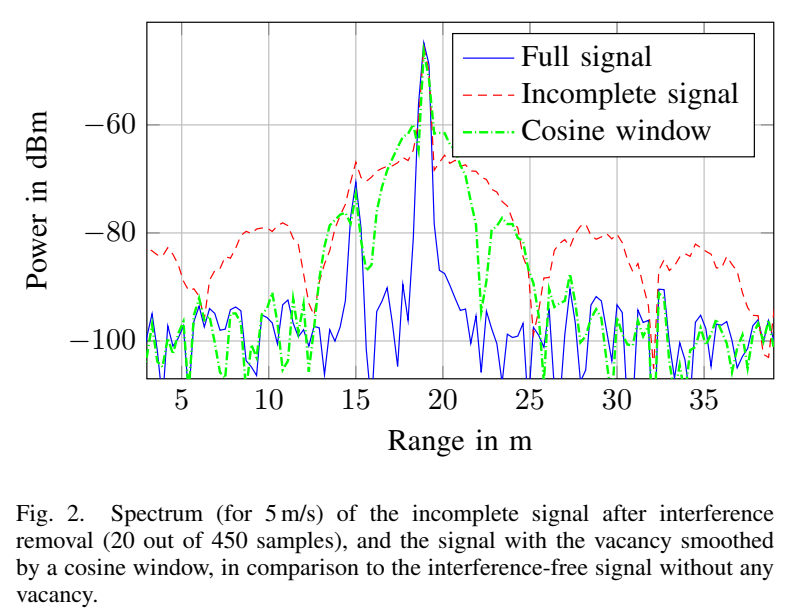
- 蓝色 (Full signal): 理想无干扰;19 m 处卡车(强峰)与 15 m 处自行车(弱峰)清晰可见。
- 红色 (Incomplete signal): 置零后强目标的能量经"缺口"引入的 si\mathrm{si}si 旁瓣扩散,在 10--18 m 与 20--30 m 出现高伪影,完全掩盖 15 m 自行车。
- 绿色 (Cosine window): 用余弦窗平滑缺口虽能降低旁瓣,但仍足以淹没自行车。
解决方案:IMAT 稀疏信号恢复
为根治"缺口"问题,论文提出 IMAT(Iterative Method with Adaptive Thresholding,带自适应阈值的迭代方法) 对丢失样本进行重建,属于稀疏信号处理/压缩感知范式。
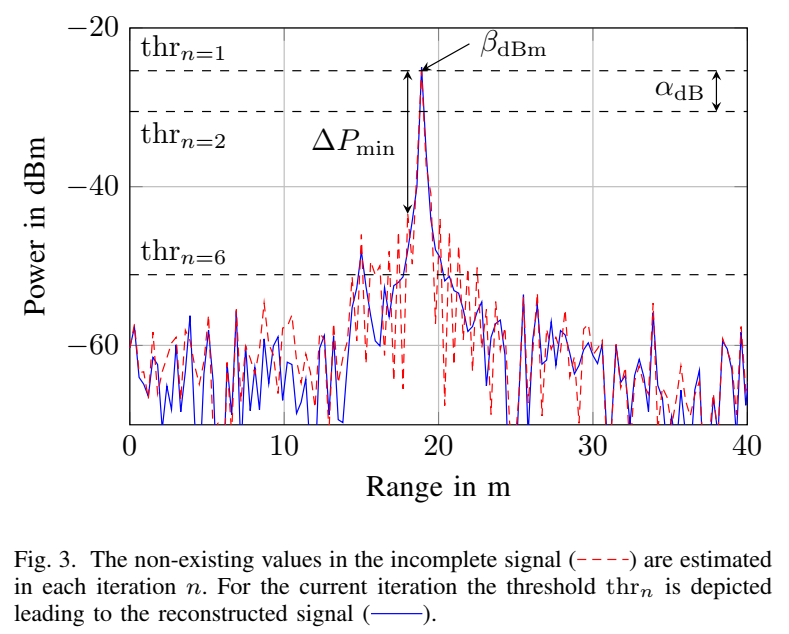
IMAT 核心步骤:
-
初始化: 从不完整信号(置零后)的频谱 Sincomplete(f)S_{\mathrm{incomplete}}(f)Sincomplete(f) 开始。
-
寻找峰值: 找到频谱最高峰值 β\betaβ(常以 dBm 表示为 βdBm\beta_{\mathrm{dBm}}βdBm)。
-
设定自适应阈值: 阈值随迭代指数下降:
thrn=β e−αn, thr_n=\beta\,e^{-\alpha n}, thrn=βe−αn,
其中 α>0\alpha>0α>0 控制下降速率。若以 dB 标度,则等价为每次迭代下降 αdB\alpha_{\mathrm{dB}}αdB。
-
频谱门限: 保留当前频谱中高于 thrnthr_nthrn 的分量,丢弃低于阈值的噪声与大部分伪影。
-
时域重建: 对保留分量做 IFFT,得近似时域 sapprox(t)s_{\mathrm{approx}}(t)sapprox(t)。
-
填补缺口: 用 sapprox(t)s_{\mathrm{approx}}(t)sapprox(t) 在缺口位置的样值回填原始时域的缺失样本。
-
迭代更新: 令 n←n+1n\leftarrow n+1n←n+1,降低阈值,重复 4--6。
自适应参数选择要点:
-
下降步长 αdB\alpha_{\mathrm{dB}}αdB: 为避免将"缺口旁瓣"误判为真信号,设定
m αdB=ΔPmin, m\,\alpha_{\mathrm{dB}}=\Delta P_{\min}, mαdB=ΔPmin,
其中 ΔPmin\Delta P_{\min}ΔPmin 为主峰与伪影之间的最小功率差,mmm 为希望跨越该差值所需的迭代数(如 m=3m=3m=3)。这样前几次仅利用最可信的强峰重建。
-
停止条件 nnn: 为防止阈值降至噪声地板之下(把噪声也"重建"进来),要求最终阈值仍高于噪声 NNN(例如留 10 dB 裕量):
n<βdBm−(N+10 dB)αdB. n<\frac{\beta_{\mathrm{dBm}}-(N+10~\text{dB})}{\alpha_{\mathrm{dB}}}. n<αdBβdBm−(N+10 dB).
(文中示例给出 αdB=5.14 dB\alpha_{\mathrm{dB}}=5.14~\text{dB}αdB=5.14 dB、βdBm=−36.3 dBm\beta_{\mathrm{dBm}}=-36.3~\text{dBm}βdBm=−36.3 dBm,最佳停止于 n=9n=9n=9。)
IMAT 算法恢复结果
通过自适应迭代,IMAT 逐步"雕琢"出真实频谱并抑制伪影。
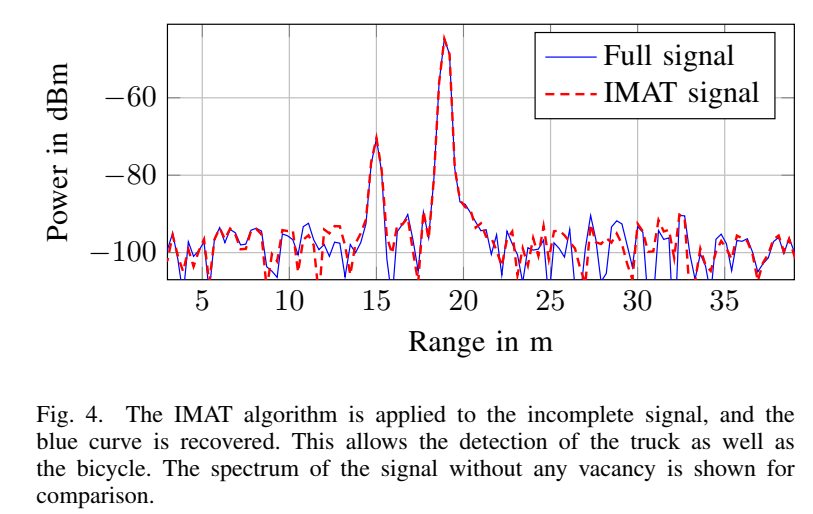
- 图 4(频谱): "IMAT signal"(红虚线)保留 19 m 卡车强峰的同时,成功从伪影中"拯救"了 15 m 自行车弱峰。
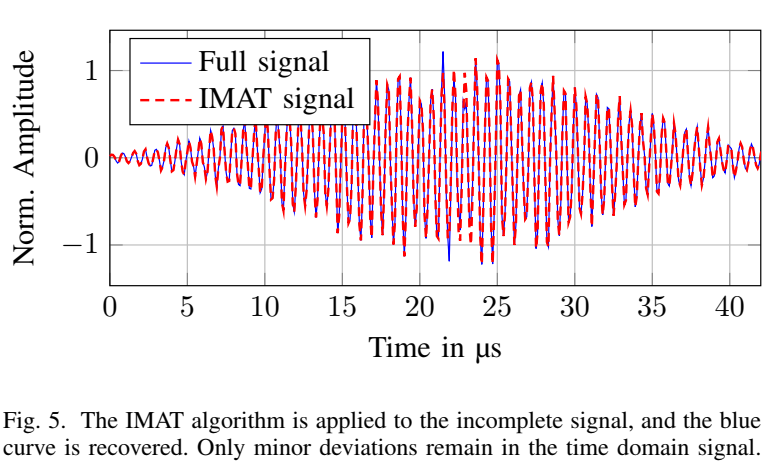
- 图 5(时域): IMAT 在缺口区域的重建波形与"Full signal"高度一致,表明高保真重构。
仿真评估与测量验证
仿真评估(Section III)
作者通过改变干扰雷达斜率,模拟不同缺口比例(10%--55%),评估自行车(弱目标)恢复后的相位均方根误差 (RMSE) Δφ\Delta\varphiΔφ(见图 6)。
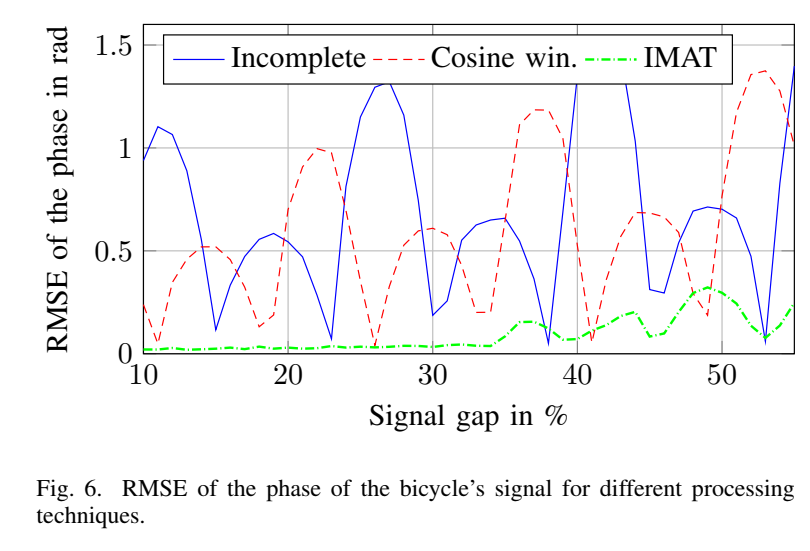
- 蓝色 (Incomplete) 与 红虚线 (Cosine win.) :相位误差大(可至 1.5 rad1.5~\text{rad}1.5 rad)且随缺口比例呈周期性起伏,因旁瓣峰/谷周期性扫过弱目标位置。
- 绿色 (IMAT) :表现显著优于前两者;在缺口达 35% 时,Δφ\Delta\varphiΔφ 仍接近 0。
文中表 III--VI 进一步量化:例如缺口 10--15% 时,IMAT 的相位误差 Δφ≈0.03 rad\Delta\varphi\approx 0.03~\text{rad}Δφ≈0.03 rad,而 Incomplete 约为 0.6 rad0.6~\text{rad}0.6 rad;幅度误差 ΔA\Delta AΔA 亦显著更小。
测量验证(Section IV)
实际测量场景包含三个近距离目标,其中一个目标(600 kHz600~\text{kHz}600 kHz 处)极弱。
-
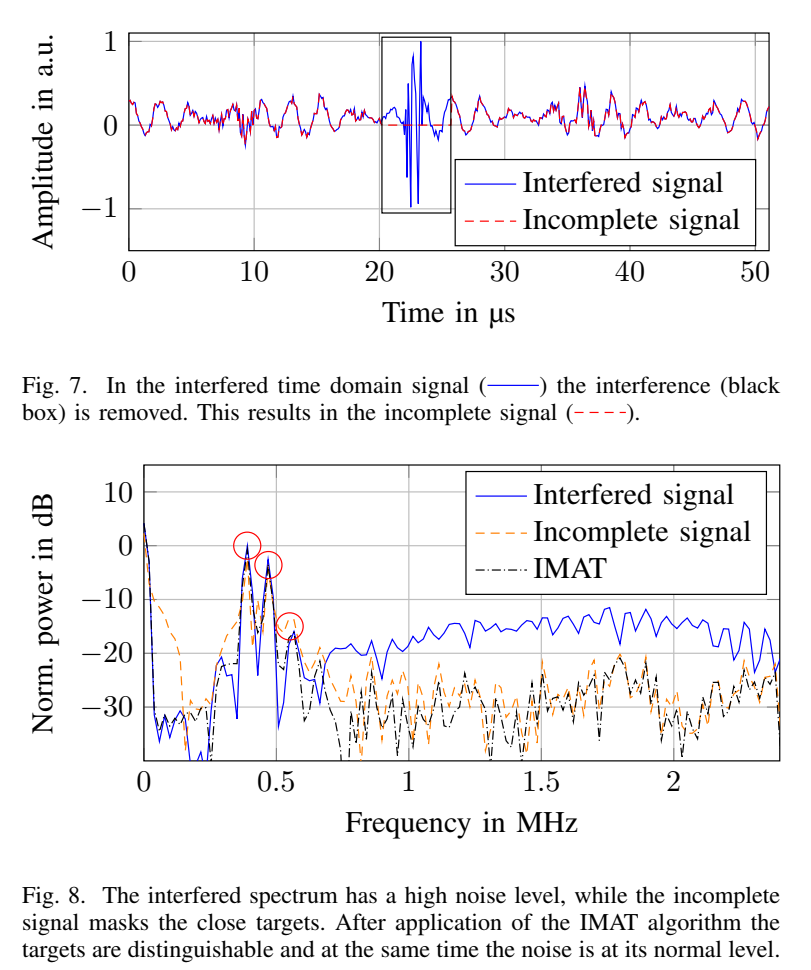
图 7: 实测干扰为高幅尖脉冲;移除后得到不完整信号(红虚线)。
-
图 8: 三种状态对比:
- 蓝色 (Interfered) :干扰将噪声地板抬高约 20 dB,所有目标被淹没;
- 黄色 (Incomplete) :置零后地板恢复,但强目标旁瓣掩盖 0.6 MHz0.6~\text{MHz}0.6 MHz 的弱目标;
- 黑色 (IMAT) :伪影被抑制且地板低,三个目标(含 0.6 MHz0.6~\text{MHz}0.6 MHz 的弱目标,红圈标出)均清晰可辨。
结论
为有效减轻雷达干扰,尤其在强目标遮挡弱目标的高动态范围场景下,单纯置零 或平滑受扰样本并不足够,因为由此引入的"缺口"会在频域产生强旁瓣伪影,掩盖弱目标。
正确做法是:对受干扰样本进行重建。
本文提出的 IMAT 稀疏采样算法 利用频域稀疏性与自适应迭代门限,能在挑战性场景下准确恢复丢失分量,显著提升检测性能,且已通过仿真与实测充分验证。
附录:关键数学推导
核心在于理解干扰持续时间与"缺口"频谱的来源。
1. 干扰持续时间 TIntT_{\mathrm{Int}}TInt(公式 1)
FMCW 干扰源于两雷达信号的混频。当两雷达调频斜率不同,其拍频 fb(t)f_b(t)fb(t) 的变化率为斜率差:
ΔS=∣STruck−SCar∣=∣BTruckTTruck−BCarTCar∣. \Delta S=\bigl|S_{\mathrm{Truck}}-S_{\mathrm{Car}}\bigr| =\left|\frac{B_{\mathrm{Truck}}}{T_{\mathrm{Truck}}}-\frac{B_{\mathrm{Car}}}{T_{\mathrm{Car}}}\right|. ΔS= STruck−SCar = TTruckBTruck−TCarBCar .
接收机 IF 带宽为 BRxB_{\mathrm{Rx}}BRx。干扰仅在 fb(t)f_b(t)fb(t) 落入通带时被接收。定义 TIntT_{\mathrm{Int}}TInt 为拍频扫过通带所需时间。若拍频从 −BRx-B_{\mathrm{Rx}}−BRx 扫到 +BRx+B_{\mathrm{Rx}}+BRx(复基带),总带宽为 2BRx2B_{\mathrm{Rx}}2BRx,故
TInt=2BRxΔS. T_{\mathrm{Int}}=\frac{2B_{\mathrm{Rx}}}{\Delta S}. TInt=ΔS2BRx.
代入数值即得约 2 μs2~\mu s2 μs。
2. "缺口"信号的频谱 S(f)S(f)S(f)(公式 3)
将时域信号视作"完整"减"缺口":
s(t)=sfull(t)−sgap(t), s(t)=s_{\mathrm{full}}(t)-s_{\mathrm{gap}}(t), s(t)=sfull(t)−sgap(t),
其中
sfull(t)=A0cos(2πf0t) rect (tT),sgap(t)=A0cos(2πf0t) rect (tTInt). s_{\mathrm{full}}(t)=A_0\cos(2\pi f_0 t)\,\operatorname{rect}\!\Bigl(\tfrac{t}{T}\Bigr),\quad s_{\mathrm{gap}}(t)=A_0\cos(2\pi f_0 t)\,\operatorname{rect}\!\Bigl(\tfrac{t}{T_{\mathrm{Int}}}\Bigr). sfull(t)=A0cos(2πf0t)rect(Tt),sgap(t)=A0cos(2πf0t)rect(TIntt).
利用卷积定理(时域相乘 ↔ 频域卷积)与
F{cos(2πf0t)}=12[δ(f−f0)+δ(f+f0)],F {rect (tτ)}=τ si(πτf), \mathcal{F}\{\cos(2\pi f_0 t)\}=\tfrac{1}{2}\bigl[\delta(f-f_0)+\delta(f+f_0)\bigr],\quad \mathcal{F}\!\left\{\operatorname{rect}\!\Bigl(\tfrac{t}{\tau}\Bigr)\right\} =\tau\,\mathrm{si}(\pi \tau f), F{cos(2πf0t)}=21[δ(f−f0)+δ(f+f0)],F{rect(τt)}=τsi(πτf),
得到
S(f)=A02[δ(f−f0)+δ(f+f0)]∗[T si(πTf)−TInt si(πTIntf)]. \begin{aligned} S(f) &=\frac{A_0}{2}\bigl[\delta(f-f_0)+\delta(f+f_0)\bigr]\ast \Bigl[T\,\mathrm{si}(\pi T f)-T_{\mathrm{Int}}\,\mathrm{si}(\pi T_{\mathrm{Int}} f)\Bigr]. \end{aligned} S(f)=2A0[δ(f−f0)+δ(f+f0)]∗[Tsi(πTf)−TIntsi(πTIntf)].
若仅关心正频部分(δ(f−f0)\delta(f-f_0)δ(f−f0) 项),可写作
S(f)∣f>0≈A02 δ(f−f0)∗[T si(πTf)−TInt si(πTIntf)]. S(f)\Big|{f>0}\approx \frac{A_0}{2}\,\delta(f-f_0)\ast \Bigl[T\,\mathrm{si}(\pi T f)-T{\mathrm{Int}}\,\mathrm{si}(\pi T_{\mathrm{Int}} f)\Bigr]. S(f) f>0≈2A0δ(f−f0)∗[Tsi(πTf)−TIntsi(πTIntf)].
注:本文统一使用 si(x)=sin(x)/x\mathrm{si}(x)=\sin(x)/xsi(x)=sin(x)/x 记号;与常见 sinc(⋅)\operatorname{sinc}(\cdot)sinc(⋅) 形式等价,差别仅在归一化约定。