“自然搞懂”深度学习系列（基于Pytorch架构）——02小试牛刀

Victory_orsh2025-10-27 15:44

Forester's Notebook

🤸‍♂️生活座右铭：勤而拂拭，莫染尘埃。 📚学习座右铭：一切烦恼来源于定义不清。 🙌留言：有任何问题欢迎交流学习，直接私信即可，一定会回！👌

"自然搞懂"深度学习（基于Pytorch架构）

文章目录

  • [Forester's Notebook](#Forester's Notebook)
    • "自然搞懂"深度学习（基于Pytorch架构）
      • [第Ⅰ章 初入茅庐](#第Ⅰ章 初入茅庐)
      • [第Ⅱ章 小试牛刀](#第Ⅱ章 小试牛刀)
        • 一、线性回归
          • [1.1 Prepare Dataset](#1.1 Prepare Dataset)
          • [1.2 Design model using class](#1.2 Design model using class)
          • [1.3 Construct loss and optimizer](#1.3 Construct loss and optimizer)
          • [1.4 Train cycle](#1.4 Train cycle)
        • 二、逻辑斯蒂回归
          • [2.1 问题讲解](#2.1 问题讲解)
          • [2.2 代码实践](#2.2 代码实践)
        • 三、DataLoader完整流程
          • [3.1 python组件间关系](#3.1 python组件间关系)
          • [3.2 Prepare Dataset](#3.2 Prepare Dataset)
          • [3.3 Design model using class](#3.3 Design model using class)
          • [3.4 Construct loss and optimizer](#3.4 Construct loss and optimizer)
          • [3.5 Train cycle](#3.5 Train cycle)
        • 四、多分类问题
          • [4.1 问题讲解](#4.1 问题讲解)
          • [4.2 代码实践](#4.2 代码实践)

第Ⅰ章 初入茅庐

第Ⅰ章 初入茅庐

第Ⅱ章 小试牛刀

在初入茅庐后，我们首先将神经网络应用到较为简单的回归、分类问题中去，综合代码实践，知行合一。

一、线性回归

第Ⅰ章中，我们就是以线性回归举例的，所以我们围绕代码进行回顾及展开。

++值得注意：本小节的四个环节（四部曲）即为深度学习标准处理流程，为保障阅读体验，各小节完整代码放于文末，参考刘二大人视频讲解++。

1.1 Prepare Dataset
python 复制代码 
# 库------类------对象------实例
import torch
# 1. Prepare Dataset
x_data = torch.Tensor([[1.0],[2.0],[3.0]])  #创建二维张量（2D Tensor）
y_data = torch.Tensor([[2.0],[4.0],[6.0]])  #3个样本，1个特征

首先，主角登场：torch包------PyTorch核心包，其主要模块如下，都将是我们之后的常驻嘉宾：

模块 作用 举例
torch 基础张量操作 torch.tensor(), torch.mean()
torch.nn 构建神经网络层与模型 nn.Linear, nn.ReLU, nn.Module
torch.optim 各种优化算法 optim.SGD, optim.Adam
torch.utils.data 数据加载工具 DataLoader, Dataset
torch.autograd 自动求导机制 loss.backward()
torch.cuda GPU 控制与计算 torch.cuda.is_available()
torchvision (扩展包) 图像数据集、模型、预处理 transforms, datasets.CIFAR10

将其尽可能联系起来：

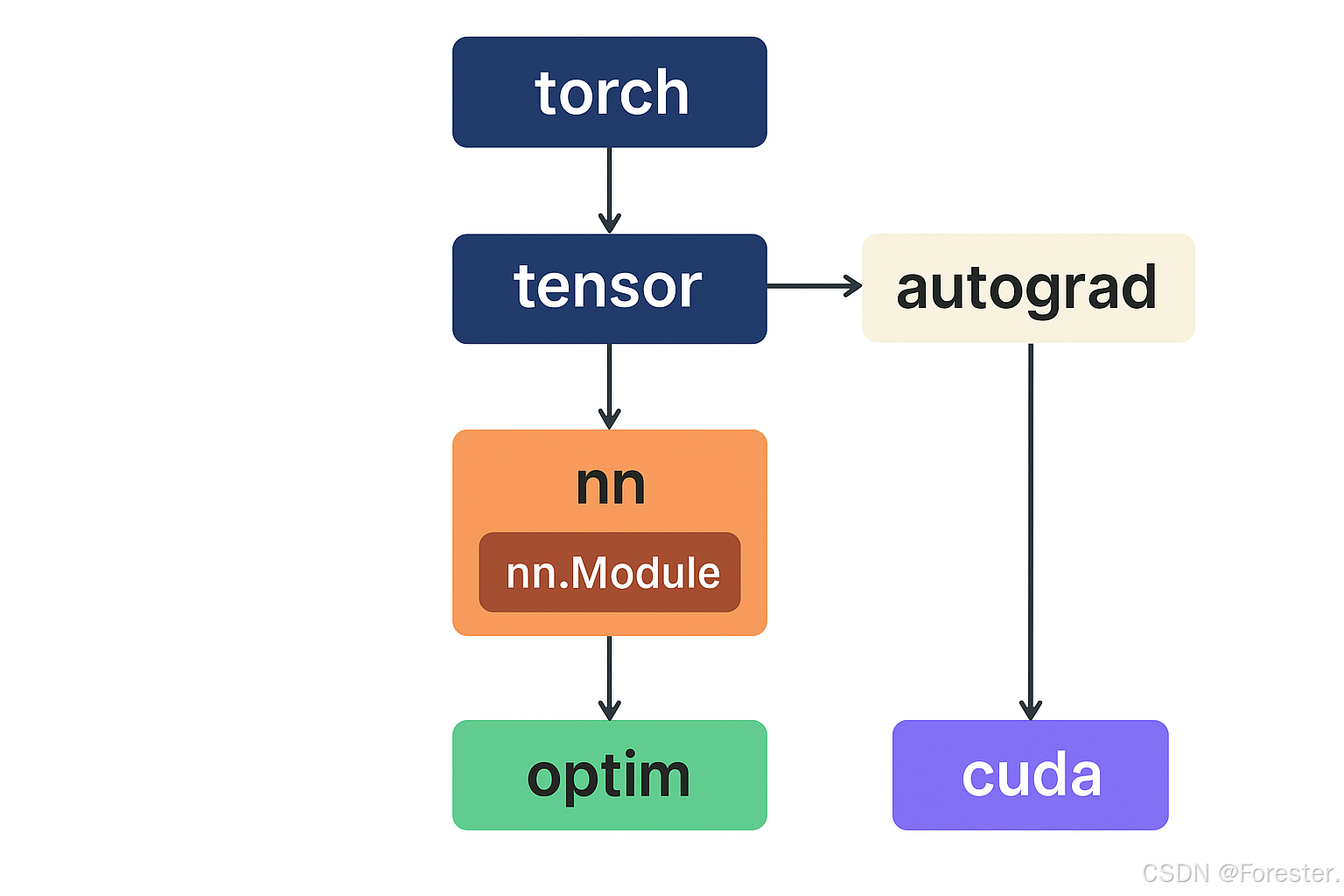
PyTorch 从 torch 模块出发，用 tensor 表示数据，autograd 实现自动求导，nn.Module 构建模型，optim 更新参数，最后通过 cuda 实现 GPU 加速。

接着，选取y=2x的3个点作为数据集，并将其转为张量------深度学习的基础单位。

Think-Help

张量（Tensor）就是多维数组，是标量、向量、矩阵的推广，有很好的数学表达性、可并行性和可求导性。

1.2 Design model using class
python 复制代码 
# 2. Design model using class
class LinearModel(torch.nn.Module):  #该类继承自Module类
    def __init__(self):  #每次创建对象时调用
        super(LinearModel,self).__init__()   #调用父类的初始化
        self.linear = torch.nn.Linear(1,1)  #装一个线性层：y=wx+b

    def forward(self,x):  #当后续执行 model(x) 时，自动调用这个 forward 函数
        y_pred = self.linear(x)  #将输入x丢进线性层
        return y_pred
model = LinearModel()

使用线性模型类搭建神经网络

首先初始化：继承父类的方法（如注册网络层、管理参数、模块嵌套支持及模型保存），然后构建你的网络层（层类、层数、每层神经元数量）；然后定义前向传播规则（得到初始计算值后如何做，通常加激活函数，返回最终预测值）；最后实例化线性模型为model。

1.3 Construct loss and optimizer
python 复制代码 
# 3. Construct loss and optimizer
criterion = torch.nn.MSELoss(reduction='sum')  #创建对象，调用MSELoss类，设置误差求和而非平均
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)  #model.parameters()寻找所有待更新参数

选择损失函数及优化器

根据问题类型选择损失函数，这里为MSE均方误差，优化器通常选择SGD。

Think-Help

损失函数的计算方式没有严格要求，但应注意：++是否取平均等操作会影响学习率的选择++ ，因为求导后1/N仍然存在，如下图：
θ : = θ − η ⋅ 1 N ∑ i = 1 N ∇ θ L ( f ( x i ; θ ) , y i ) \theta := \theta - \eta \cdot \frac{1}{N} \sum_{i=1}^{N} \nabla_\theta L(f(x_i;\theta), y_i) θ:=θ−η⋅N1i=1∑N∇θL(f(xi;θ),yi)

1.4 Train cycle
python 复制代码 
# 4. Train cycle
for epoch in range(1000):
    #前向传播
    y_pred = model(x_data)
    loss = criterion(y_pred,y_data)  #实例化对象
    print(epoch,loss.item())
    #反向传播
    optimizer.zero_grad()  #清空上一次计算的梯度（否则梯度会累加）
    loss.backward()  #自动计算每个参数的梯度
    optimizer.step()  #更新参数

进入训练周期

从这里可以明显看出该线性模型使用All（传统随机梯度下降GD，即使用一组样本进行一次参数更新），首先前向传播：计算最终预测值、损失函数并输出；然后反向传播：梯度清空、计算当前梯度、参数更新。

python 复制代码 
print("w = ",model.linear.weight.item())  #.item() 把张量里的数值提取为普通的Python数字
print("b = ",model.linear.bias.item())

x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print("y_pred = ",y_test.data)  #.data：返回张量的实际数据部分
#tensor.data 仍然是张量（Tensor），但它不再追踪梯度，也不在计算图中

最后进行测试及所需其它操作。

二、逻辑斯蒂回归
2.1 问题讲解

有趣的是，Logistics回归虽然叫回归，但实际是一种二分类方法，简单来说，它相比线性回归只增添了一个Sigmoid函数，将线性回归的输出值代入Sigmoid中实现分类。
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1

如图所示：

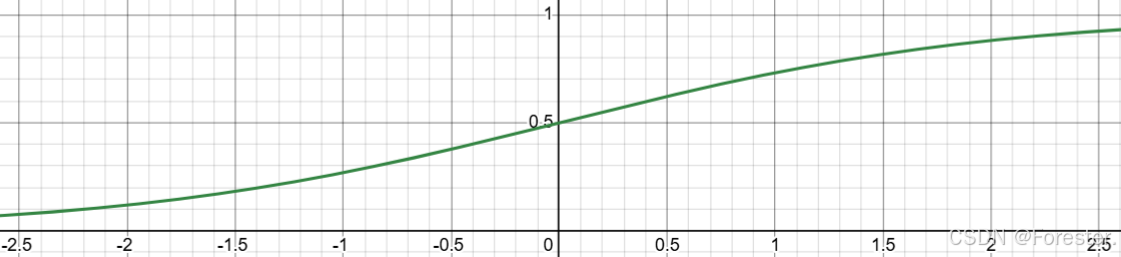
故无论线性回归输出值是什么一定能将其转为（0，1）范围之间，将连续值转化为概率值实现分类。

同时，需要一起变化的还有损失函数，最常用的二分类（y=0/1）损失函数即为BCELoss（Binary Cross Entropy Loss，二元交叉熵损失函数 ），对于单个样本：
L ( y , y ^ ) = − [ y log ⁡ ( y ^ ) + ( 1 − y ) log ⁡ ( 1 − y ^ ) ] L(y, \hat{y}) = - \left[ y \log(\hat{y}) + (1 - y) \log(1 - \hat{y}) \right] L(y,y^)=−[ylog(y^)+(1−y)log(1−y^)]

对于N个样本取平均损失：
BCE Loss = − 1 N ∑ i = 1 N [ y i log ⁡ ( y ^ i ) + ( 1 − y i ) log ⁡ ( 1 − y ^ i ) ] \text{BCE Loss} = -\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] BCE Loss=−N1i=1∑N[yilog(y^i)+(1−yi)log(1−y^i)]

Think-Help

用于记录当前模型输出的概率与真实标签的差距，为什么能做到呢？

首先要明确通常预测y值指的是预测为正类的概率值，即：
y ^ = P ( y = 1 ∣ x ) \hat{y} = P(y = 1 | x) y^=P(y=1∣x)

则：
L = − l o g ( 1 − y ^ ) , y = 0 L = − l o g ( y ^ ) , y = 1 L=-log(1-\hat{y}),y=0\\ L=-log(\hat{y}),y=1 L=−log(1−y^),y=0L=−log(y^),y=1

也就实现了预测正确的概率值越大，损失越小。

2.2 代码实践

在代码中，仅设计模型处多加一个Sigmoid函数，损失函数换为BCELoss即可。

python 复制代码 
# 1、Design model using Class
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel, self).__init__()
        self.linear = torch.nn.Linear(1,1)

    def forward(self, x):
        y_pred = torch.sigmoid(self.linear(x))  # 此处加了sigmoid函数，对初始输出值进行sigmoid处理
        return y_pred
model = LogisticRegressionModel()

# 2、Construct loss and optimizer
criterion = torch.nn.BCELoss(size_average=False)   # Key：是否取均值影响学习率设置：Loss是否乘以1/N------Loss对参数的梯度是否乘以1/N
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
三、DataLoader完整流程

在前两节我们的参数更新方法都是All（传统GD），但在第Ⅰ章我们提到了最常用的是Mini-Batch方法，如何实现呢？就要使用DataLoader。

3.1 python组件间关系

++补充一下python基本知识点------组件间的关系++

python 复制代码 
程序库 Library（比如 PyTorch）
 ├── 包 Package（torch、torch.nn、torch.utils）
 │     ├── 模块 Module（torch.nn.functional）
 │     │     ├── 类 Class（Linear, MSELoss 等）
 │     │     └── 函数 Function（sigmoid(), relu() 等）
 │     └── 子包 Subpackage（torch.utils.data）
 └── ...

在 PyTorch 中，DataLoader 属于 数据加载模块（torch.utils.data） 下的一个类（Class）。

3.2 Prepare Dataset

定义类进行完善的数据处理是个好习惯。

python 复制代码 
# 1.Prepare Dataset
class DiabetesDataset(Dataset):
    def __init__(self, filepath):
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32, skiprows=1)  # 第一行为标题列，无法转浮点型
        self.len = xy.shape[0]  # 查看第一列，即有多少个样本
        self.x_data = torch.from_numpy(xy[:, :-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])
    '''
    Think-Help
    xy------numpy数组   形状：（样本数，特征数+1）
    xy[:, :-1] 取所有样本的前N-1列，即所有特征
    xy[:, [-1]] 取所有样本的第N列，即标注值
    torch.from_numpy 即将numpy数组转为pytorch张量，共享内存（不新建，一改具改）。
    注：xy[:, -1]和xy[:, [-1]]不同，前者是一维数组，后者仍是二维矩阵。
    '''
    def __getitem__(self, index):
        return self.x_data[index], self.y_data[index]

    def __len__(self):
        return self.len
    '''
    Think-Help
    Magic Method------魔法方法，即带有双下划线的方法，
    定义：不会被直接调用，隐式自动触发
    例：执行model = LinearModel()后，自动调用__new__ and __init__
    Python 的设计哲学：Everything is an object
    '''
dataset = DiabetesDataset('./dataset/pima-indians-diabetes.csv')  #文件链接：https://github.com/Xueyouing/Study-Naturally
train_loader = DataLoader(dataset=dataset, batch_size=32, shuffle=True, num_workers=4)

注意最后一行，从传入参数也可以看出DataLoader决定mini-batch中样本数量，是否打乱及并行方式。

3.3 Design model using class
python 复制代码 
# 2.Design model using class
class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.sigmoid = torch.nn.Sigmoid()

    def forward(self, x):
        x = self.sigmoid(self.linear1(x))
        x = self.sigmoid(self.linear2(x))
        x = self.sigmoid(self.linear3(x))
        return x

model = Model() #实例化

神经网络对应形式（从第一个隐含层开始输入值都要经过激活函数Sigmoid计算）：

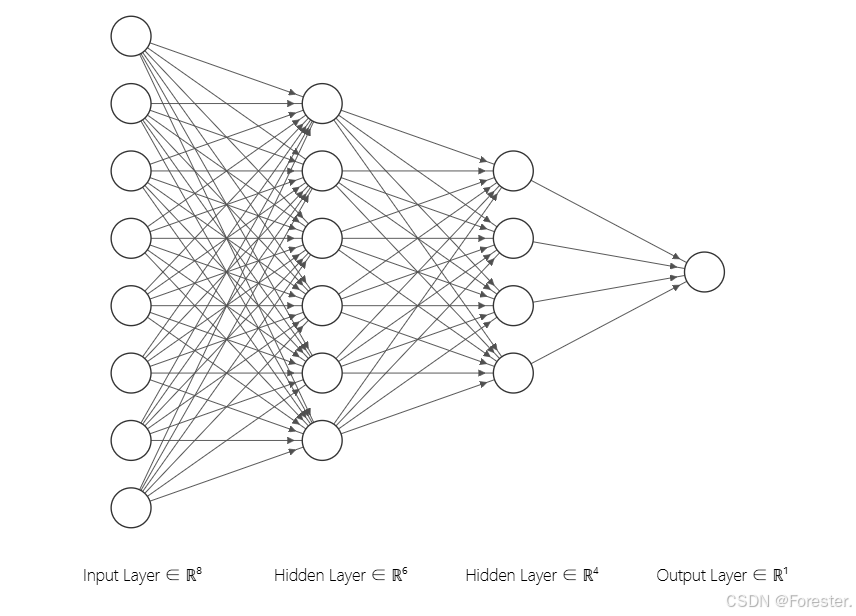
3.4 Construct loss and optimizer
python 复制代码 
# 3.Construct loss and optimizer
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

Think-Help
torch.optim.SGD 的名字虽然叫 "Stochastic Gradient Descent"，但它并不强制你一个样本一个样本地更新。

Saying again：是否使用 mini-batch（小批量样本） ， 其实是由 你怎么喂数据（DataLoader） 决定的，而不是优化器。

3.5 Train cycle
py 复制代码 
# 4.Train cycle
if __name__ == '__main__':
    for epoch in range(100):
        for i,data in enumerate(train_loader, 0):  
            inputs, labels = data
            y_pred = model(inputs)
            loss = criterion(y_pred, labels)
            print(epoch, i, loss.item())

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

'''
Think-Help
if __name__ == '__main__':当该脚本被直接执行时运行。这里是为了防止trainloader报错。
enumerate返回索引i及数据值data，其中data又分为（inputs，labels）
0指从第0批次开始。
'''

很关键的不同点，第二层循环即指代每个epoch分批量使用数据集进行参数更新。

四、多分类问题
4.1 问题讲解

对于多分类问题，自然仍先要找到适合它的损失函数。

首先要明确分类问题的两个条件：最终各类别概率值大于0；各类别概率值之和等于1。

我们可以先回顾一下二分类问题的求解过程：输出层得到一个输出值，代入Sigmoid函数得到P(y=1|x)的概率值，P(y=0|x)=1-P(y=1|x)，满足要求，损失函数可以计算。

而多分类如何满足呢？输出层不止一个结点，会得到多个输出值。

显然，仍将输出值都代入Sigmoid函数无法满足要求，而另一个函数却可以------Softmax函数：
P ( y = i ) = e z i ∑ j = 0 K − 1 e z j , i ∈ { 0 , . . . , K − 1 } P(y = i) = \frac{e^{z_i}}{\sum_{j=0}^{K-1} e^{z_j}}, i \in \{0, ..., K - 1\} P(y=i)=∑j=0K−1ezjezi,i∈{0,...,K−1}

其中z便是输出值，将全部K个值都带入，会得到一个"值都大于0且K个值和为1的分布"。

得到概率值后，如何计算损失呢？

Loss = − log ⁡ ( y ^ c ) \text{Loss} = -\log(\hat{y}_c) Loss=−log(y^c)

其中yc表示预测正确类别的概率，概率值越高，损失越小。

Think-Help

二分类和多分类的损失函数实际是一样的，都是取预测正确类别的概率进行-log()，以实现**"预测正确的概率值越高，损失越小"**。

思路讲解完毕，来看具体实现。

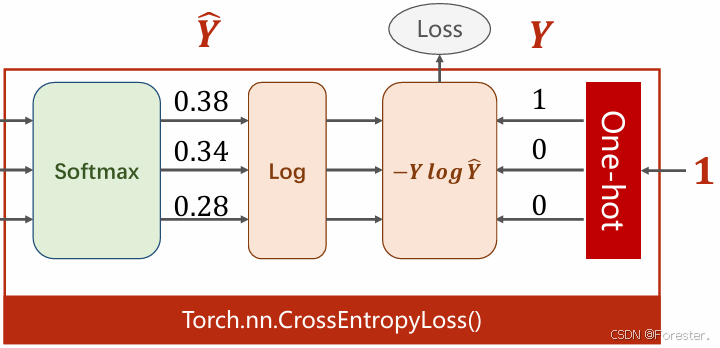
图释：输出值，经过Softmax函数得到概率值，对应乘以独热编码后，只剩下了-log(yc)一项。

整体流程叫做交叉熵损失函数（CrossEntropyLoss），而-log(yc)叫做负对数似然损失（NLLLoss，Negative Log Likelihood Loss）。

二者的关系为：CrossEntropyLoss = Softmax + NLLLoss。

Think-Help

在实际编程时，你会看到log_softmax函数，如下：

py 复制代码 
log_probs = F.log_softmax(logits, dim=1)
loss = F.nll_loss(log_probs, target)

不要惊讶，这是因为考虑到数值稳定性（不会出现 exp(大数) 或 log(接近 0) 的溢出问题），要将softmax和log共同进行：
log ⁡ ( e z i ∑ j e z j ) = z i − log ⁡ ( ∑ j e z j ) \log\left(\frac{e^{z_i}}{\sum_j e^{z_j}}\right) = z_i - \log\left(\sum_j e^{z_j}\right) log(∑jezjezi)=zi−log(j∑ezj)

而nll_loss实际只起到了取值并取负的操作。

4.2 代码实践

本节实践是经典手写数字图像MNIST数据集，要求识别0-9的多分类问题。

流程仍是四部曲，重点在于使用到了图像识别的专用工具和操作，已在代码中详细注释。

python 复制代码 
import torch
from torchvision import transforms  # 图像预处理
from torchvision import datasets  # 图像数据集加载
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

# 1.Prepare dataset
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
'''
ToTensor将图片转为张量，Normalize将其像素值转为[0, 1]区间（标准化）
(0.2307,) 是整个数据集中所有像素的 平均值（mean）；
(0.3081,) 是所有像素的 标准差（std）；
Because：神经网络更喜欢正态分布数据【加快收敛速度、防止某些特征主导模型、保持激活函数在有效区间工作等】
'''
train_dataset = datasets.MNIST(root='../L_Pytorch/dataset', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../L_Pytorch/dataset', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)

# 2.Design model using class
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)

    def forward(self, x):
        x = x.view(-1, 784)  # 获得batch_size，摊平图片维度
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x)

model = Net()

# 3.Construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 动量使收敛更快、更稳定：每次参数更新时，有 50% 的"惯性"来自上一次的梯度方向。

# 4.Train cycle
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, targets = data
        outputs = model(inputs)
        loss = criterion(outputs, targets)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:  # 下标从0开始
            print(f"[{epoch+1}, {batch_idx+1:5d}] loss: {running_loss/300:.3f}")
            running_loss = 0

def test():
    correct = 0
    total = 0
    with torch.no_grad():  # 测试无需更新参数，故不用计算梯度
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, prediction = torch.max(outputs.data, dim=1)
            '''
            Think-Help
            torch.max(tensor, dim=1)：在指定维度 dim=1 上求最大值。
            返回两个结果： 第一维是最大值；第二维是最大值所在的位置（索引 index）。
            我们取概率值最大的类别索引，只关心类别索引而不关心概率值。
            '''
            total += labels.size(0)  # labels是长度为size的一维张量，每次加上当前批次（batch）的样本数量
            correct += (prediction == labels).sum().item()
    print(f'Accuracy: {correct/total}')

if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

恭喜你！又成功小试牛刀！你已经对四部曲有了深刻印象，这是很好的基础！同时可以自己设计基础神经网络并应用到简单的回归分类任务中去！

接下来让我们学习当下最流行的神经网络架构！

  • 本文由Forester原创撰写，无偿分享，若发现侵犯版权、转卖倒卖等行为，追究其责任。

  • 为保证文体美观，各小节完整代码及PDF笔记已上传至GitHub：Xueyouing/Study-Naturally。

  • 欢迎关注，未完待续！

相关推荐
tzc_fly3 小时前
DeepSeek-OCR：上下文光学压缩
人工智能·计算机视觉·ocr
Bruce-li__3 小时前
CI/CD流水线全解析：从概念到实践，结合Python项目实战
开发语言·python·ci/cd
37手游后端团队3 小时前
构建AI会话质检平台：技术架构与实践分享
人工智能·后端
哔哩哔哩技术3 小时前
B站游戏大模型翻译实践 —— 我们如何用LLM撑起全年百万字本地化翻译任务
人工智能
longgyy3 小时前
AI 开发告别 “孤岛”：MCP + 火山引擎
人工智能·火山引擎
珊瑚礁的猪猪侠3 小时前
正则表达式入门到精通教程（Linux实操版）
linux·人工智能·正则表达式
星空的资源小屋3 小时前
MkFont，一款开源免费的字体设计工具
网络·人工智能·pdf·电脑
mir frog3 小时前
DAY44 PYTHON 预训练模型
人工智能·深度学习·机器学习
yuzhuanhei3 小时前
机器学习算法常用算法
人工智能·算法·机器学习
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04GitLab 零基础入门指南：从安装到项目管理全流程05Linux下V2Ray安装配置指南06Burp与其他安全工具联动及代理设置教程07jdk21下载、安装（Windows、Linux、macOS）08Labelme从安装到标注：零基础完整指南09HTML5 敲击乐：从零搭建交互式前端音乐项目10NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南