
本部分围绕因果识别与估计策略展开,以潜在结果框架为核心,先点明因果推断的基本难题------无法观测个体接受与不接受处理的两种潜在结果,因此聚焦估计平均处理效应(ATE)与条件平均处理效应(CATE);接着明确因果识别的关键假设(条件可忽略性、一致性、重叠性等)并梳理符号体系,再介绍两类核心估计方法(处理建模如非参数匹配、逆倾向得分加权IPW,结果建模如回归),以及能提升稳健性的双重稳健估计器,为后续结合深度学习进行因果估计做好理论铺垫。
因果识别和估计策略
因果效应的识别
本入门读物中描述的论文主要在潜在结果因果框架(Neyman-Rubin因果模型)内构建(Rubin, 1974;Imbens和Rubin, 2015)。该框架关注识别样本中每个单元i在接受处理(Y(1))或未接受处理(Y(0))时的"潜在结果"。然而,由于每个单元在现实中只能接受一种处理方案(接受处理或不接受处理),因此不可能观察到每个个体的两种潜在结果(通常称为"因果推断的基本问题")(Holland, 1986)。虽然我们因此无法识别每个单元的个体处理效应τi=Yi(1)−Yi(0),但因果推断框架允许我们概率性地估计处理组和控制组样本的平均处理效应(ATEs)和基于选定协变量的条件平均处理效应(CATE)。在该文献中,许多论文的动机是提出既能从观察数据中推断CATE,又能对处理状态未知的样本外单元预测CATE的算法。对于不熟悉因果推断的读者,框4简要介绍了因果推断,并在框5中提供了教程中使用的具体示例。
框4:因果推断基本介绍
相关性不等于因果关系,因果推断关注识别随机变量之间的因果关系。我们想对社会数据提出的许多因果问题(对于具有特征X的单元,T对Y的因果效应是什么?)可以分解为具有以下一般格式的反事实问题:"对于具有X特征的单元,如果T发生或不发生,结果Y会是什么?"
随机对照试验(RCTs,在数据科学和行业应用中也称为A/B测试)通常被认为是回答这类问题的理想方法:每个具有协变量或特征X的单元被随机分配到处理组或控制组,随后测量结果Y。但在许多情况下,收集实验数据的成本过高或不道德(例如,随机分配学生上大学或不上大学)。在这些情况下,我们可以对观察数据(例如,关于大学入学的调查数据)进行统计调整,以接近实验理想。本文描述的方法旨在主要使用非实验观察数据回答反事实问题。
至少有三种不同的因果推断学派已在社会统计学和计量经济学(Rubin, 1974;Imbens和Rubin, 2015)、流行病学(Robins, 1986, 1987;Hernán和Robins, 2020)和计算机科学(Goldszmidt和Pearl, 1996;Pearl, 2009)中引入。这些因果框架的目标是描述和纠正数据或研究设计中阻碍人们做出真正因果声明的偏差。如果这些偏差是可纠正的,并且因果效应可以用观察数据的分布唯一表示,那么我们说因果效应是可识别的(Kennedy, 2016)。只有当因果效应可识别时,我们才能使用统计工具纠正偏差并估计因果效应(例如,逆倾向得分加权、g计算、深度学习)。
本文提出的算法主要通过纠正混杂偏差来估计因果效应。粗略地说,混杂协变量/特征是指与处理和结果都相关的变量,它会误导性地表明处理对结果有因果效应,或者掩盖处理和结果之间的真实因果关系。通常,混杂因素是处理和结果的原因。作为混杂偏差的一个例子,估计上大学(处理)对成人收入(结果)的因果效应需要控制父母收入可能是大学入学和成人收入的共同原因这一事实。
框5:应用因果推断示例:婴儿健康与发展研究
为了让不熟悉因果推断的读者更具体地了解这个问题设置,考虑基于1985-1988年婴儿健康与发展研究的模拟,该研究在该文献中被广泛用作基准。在这项实验中,早产儿被随机分配到强化、高质量的儿童保育(T),随后测量他们的认知测试分数(Y)。作者还测量了许多其他协变量X,包括"妊娠并发症、儿童出生体重和胎龄、出生顺序、儿童性别、家庭构成、日托安排、医疗保健来源、家庭环境质量、父母种族和民族、母亲年龄、教育程度、智商和就业情况"(Ramey等, 1992)。ATE是强化儿童保育对所有儿童认知分数的影响,而各种CATE可能旨在更好地理解儿童保育对女性儿童、未成年母亲所生儿童或父母失业儿童的影响如何变化。
Hill(2011)通过重新模拟结果,将这些实验数据转化为观察性基准,使得协变量X在处理和结果之间引入混杂偏差。虽然模拟并未保留协变量的名称,但我们可以设想观察性研究中可能存在的一些混杂关系。例如,假设富裕(X₁)父母更有能力负担高质量儿童保育(T),但儿童保育与早产儿认知能力(Y)之间实际上仅存在弱关联。我们还知道,富裕父母更可能进行母乳喂养(X₂),而母乳喂养与更高的认知能力呈正相关(Heck等, 2006;Kramer等, 2008)。如果我们不考虑收入与儿童保育之间的相关性(X₁→T),也不考虑收入与认知能力之间的相关性(X₁→X₂→Y),那么我们的ATE/CATE估计可能存在偏差,甚至更糟的是,可能错误地将儿童保育与认知能力之间的相关性解读为因果关系。下图展示了这个示例。
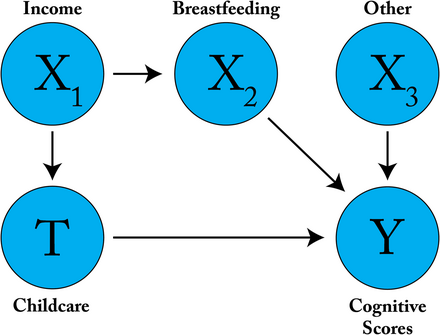
此处提出的假设性混杂偏差可通过以下方式调整:处理建模(如逆倾向得分加权、非参数深度表示学习)以阻断路径X₁→T;结果建模(如广义线性模型、深度回归)以阻断路径X₁→X₂→Y;或同时使用两种方法(见"因果效应估计"部分)。有关使用IHDP基准的代码示例,请参考教程。
ATE(平均处理效应)的定义为:
ATE=E[Y(1)−Y(0)]=1N∑i(Yi(1)−Yi(0))=1N∑iτi=E[τ] \text{ATE} = \mathbb{E}[Y(1) - Y(0)] = \frac{1}{N}\sum_{i}(Y_i(1) - Y_i(0)) = \frac{1}{N}\sum_{i}\tau_i = \mathbb{E}[\tau] ATE=E[Y(1)−Y(0)]=N1i∑(Yi(1)−Yi(0))=N1i∑τi=E[τ]
其中,Yi(1)Y_i(1)Yi(1) 和 Yi(0)Y_i(0)Yi(0) 分别表示单元 iii 接受处理和未接受处理时的潜在结果。
CATE(条件平均处理效应)的定义(符号略有简化但便于理解)为:
CATE(x)=E[Yi(1)−Yi(0)∣Xi=x]=E[τi∣Xi=x]=1N∑i∣Xi=xτi \text{CATE}(x) = \mathbb{E}[Y_i(1) - Y_i(0) \mid X_i = x] = \mathbb{E}[\tau_i \mid X_i = x] = \frac{1}{N}\sum_{i \mid X_i = x}\tau_i CATE(x)=E[Yi(1)−Yi(0)∣Xi=x]=E[τi∣Xi=x]=N1i∣Xi=x∑τi
其中,XXX 是选定的可观测协变量集合,x∈Xx \in Xx∈X 代表这些协变量的特定取值,"基于 Xi=xX_i = xXi=x 的条件"表示期望仅针对协变量 Xi=xX_i = xXi=x 的单元 iii 计算。
在本文所涉及的因果推断机器学习文献中,因果识别的主要策略是可观测选择(selection on observables)。因果识别的一大挑战在于,与处理和结果都相关的协变量可能存在混杂关系。
在存在混杂的情况下,实现因果效应识别的关键假设如下:
- 条件可忽略性/可交换性
给定协变量 XXX 时,潜在结果 Y(0)Y(0)Y(0)、Y(1)Y(1)Y(1) 与处理 TTT 条件独立,即:
Y(0),Y(1)⊥ ⊥T∣XY(0), Y(1) \perp\!\!\!\perp T \mid XY(0),Y(1)⊥⊥T∣X
条件可忽略性意味着,除观测到的协变量 XXX 外,不存在同时影响处理和结果的未观测混杂因素。此外,XXX 可包含结果的预测变量(有助于提高精度),但不应包含工具变量(会降低精度并可能放大残余偏差)或条件集合中的对撞变量[8]。
其他用于证明因果识别合理性的标准假设包括:
-
一致性/稳定单元处理值假设(SUTVA)
一致性规定,当一个单元接受处理时,其观测结果恰好等于对应的潜在结果(控制条件下的结果亦是如此)。此外,任何单元的响应不会随其他单元的处理分配而变化(即无网络效应或溢出效应),且处理的形式/水平在所有单元间均一且一致(无多种处理版本)。需注意,这是基于我们对数据生成过程的理解而提出的识别假设,与估计所选择的模型无关。其更正式的表达为:
T=t→Y=Y(T)T = t \rightarrow Y = Y(T)T=t→Y=Y(T) -
重叠性
对于所有 x∈Xx \in Xx∈X(即任何观测到的协变量取值),在由这些协变量定义的"层"内,所有处理 t∈{0,1}t \in \{0,1\}t∈{0,1} 在数据中出现的概率均非零,即:
1>p(T=t∣X=x)>01 > p(T = t \mid X = x) > 01>p(T=t∣X=x)>0 -
可逆性 (在使用神经网络进行识别与估计的交叉场景中有时会引入的额外假设)
Φ−1(Φ(X))=X\Phi^{-1}(\Phi(X)) = XΦ−1(Φ(X))=X换言之,神经网络编码的表示函数 Φ\PhiΦ 必须存在逆函数,能够从表示空间中重构出原始协变量 XXX。当使用表示学习时,这是条件可忽略性假设成立的必要条件。从实践角度看,这也意味着我们构建的表示足以捕捉所关注的因果关系。
为便于参考,我们在框6中列出了本入门读物中使用的完整符号说明。
框6:因果推断与估计的符号说明
我们使用大写字母表示一般量(如随机变量),小写字母表示单个单元的特定量(如观测变量值)。
因果识别
- 观测协变量/特征:XXX
- 潜在结果:Y(0)Y(0)Y(0) 和 Y(1)Y(1)Y(1)
- 处理:TTT
- 不可观测的个体处理效应:τi=Yi(1)−Yi(0)\tau_i = Y_i(1) - Y_i(0)τi=Yi(1)−Yi(0)
- 平均处理效应:ATE=E[Y(1)−Y(0)]=E[τ]\text{ATE} = \mathbb{E}[Y(1) - Y(0)] = \mathbb{E}[\tau]ATE=E[Y(1)−Y(0)]=E[τ]
- 条件平均处理效应:CATE(x)=E[Yi(1)−Yi(0)∣Xi=x]=E[τi∣Xi=x]\text{CATE}(x) = \mathbb{E}[Y_i(1) - Y_i(0) \mid X_i = x] = \mathbb{E}[\tau_i \mid X_i = x]CATE(x)=E[Yi(1)−Yi(0)∣Xi=x]=E[τi∣Xi=x]
深度学习估计
- 预测的潜在结果:Y^(0)\hat{Y}(0)Y^(0) 和 Y^(1)\hat{Y}(1)Y^(1)
- 结果建模函数:Y^(T)=h(X,T)\hat{Y}(T) = h(X, T)Y^(T)=h(X,T)
- 倾向得分函数:π(X,T)=P(T∣X)\pi(X, T) = P(T \mid X)π(X,T)=P(T∣X)(其中 π(X,0)=1−π(X,1)\pi(X, 0) = 1 - \pi(X, 1)π(X,0)=1−π(X,1))
- 表示函数:Φ(X)\Phi(X)Φ(X)(生成表示 ϕ\phiϕ)
- 损失函数:L(true,predicted)\mathcal{L}(\text{true}, \text{predicted})L(true,predicted)
- 损失函数缩写:MSE(均方误差)、BCE(二元交叉熵)、CCE(分类交叉熵)
- 损失超参数:λ,α,β\lambda, \alpha, \betaλ,α,β
- 单元 iii(协变量为 XiX_iXi)的估计CATE*:CATE^i=τ^i=Y^i(1)−Y^i(0)=h(Xi,1)−h(Xi,0)\hat{\text{CATE}}_i = \hat{\tau}_i = \hat{Y}_i(1) - \hat{Y}_i(0) = h(X_i, 1) - h(X_i, 0)CATE^i=τ^i=Y^i(1)−Y^i(0)=h(Xi,1)−h(Xi,0)
- 估计的ATE:ATE^=1N∑i=1Nτ^i\hat{\text{ATE}} = \frac{1}{N}\sum_{i=1}^N \hat{\tau}_iATE^=N1∑i=1Nτ^i
除ATE和CATE外,机器学习文献中还常用Hill(2011)首次提出的估计异质性效应精度(PEHE) 指标。PEHE是预测CATE的平均误差,定义为:
PEHE=1N∑i=1N(τi−τ^i)2 \text{PEHE} = \frac{1}{N}\sum_{i=1}^N (\tau_i - \hat{\tau}_i)^2 PEHE=N1i=1∑N(τi−τ^i)2
除作为具有已知反事实的模拟指标外,PEHE在该文献的泛化界构建中也具有理论意义(Shalit、Johansson和Sontag, 2017;Johansson等, 2018, 2020;Zhang、Bellot和Schaar, 2020)。
*注:我们用 τ^\hat{\tau}τ^ 表示估计的CATE,因为真正的个体处理效应无法仅通过观测协变量 XXX 来描述。
因果效应的估计
一旦确定了从可用数据中识别因果效应的策略(这可以说是因果推断中更困难且更重要的部分),就可以使用统计方法通过控制混杂偏差、选择偏差和/或测量误差来估计因果效应。估计主要有两种基本方法:处理建模 (控制协变量 XXX 与处理 TTT 之间的相关性)和结果建模 (控制协变量 XXX 与结果 YYY 之间的相关性)(图4)。下文将简要回顾三种用于消除混杂偏差的传统技术,为我们对深度学习模型的系统梳理提供铺垫。首先讨论基于回归的结果建模,然后是基于非参数匹配的处理建模,最后介绍基于IPW的处理建模,并引入双重稳健性的概念。
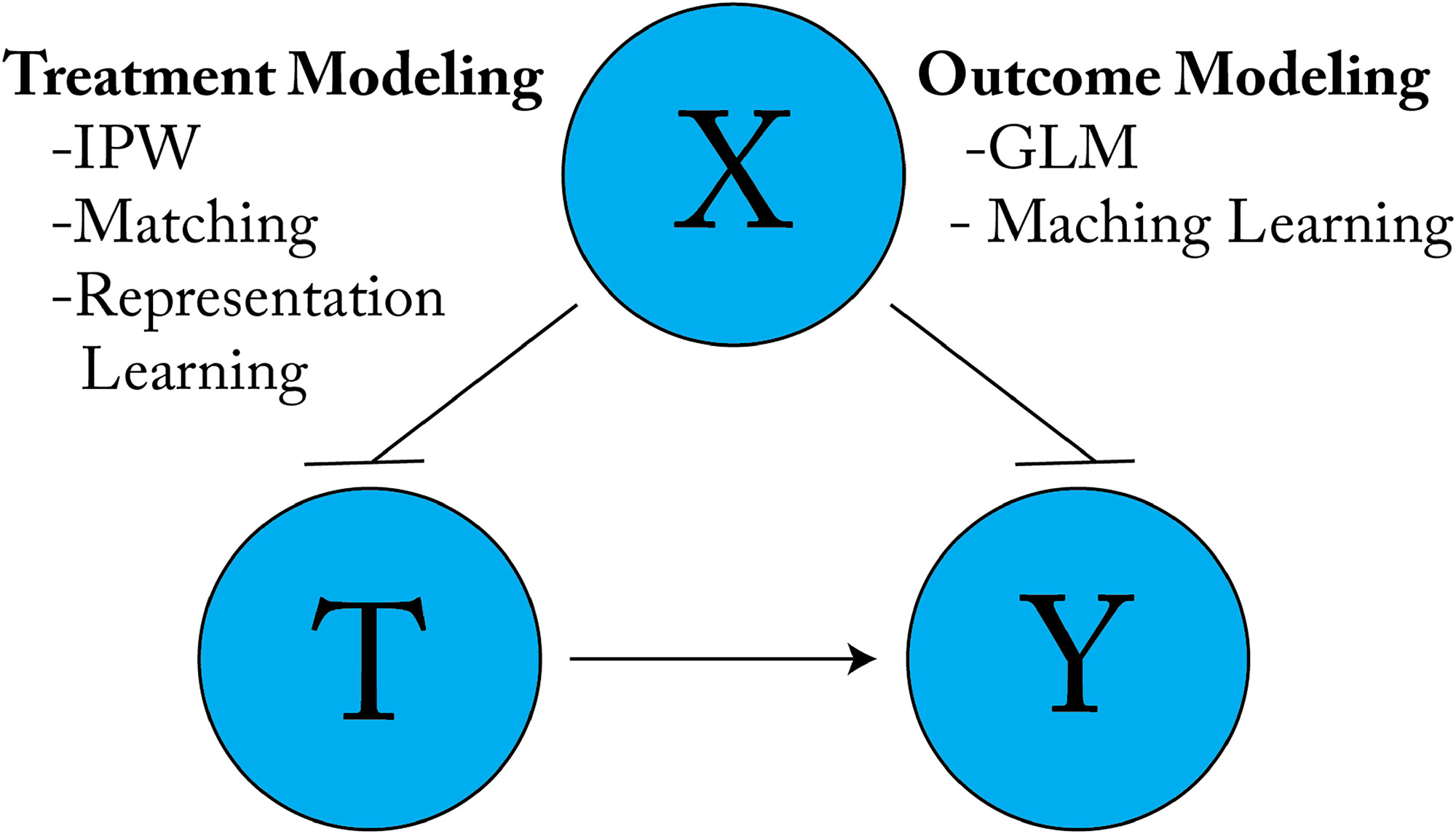
图4. 去混杂的两种基本方法。虚线箭头表示被阻断的因果路径。逆倾向得分加权、平衡和表示学习等处理建模方法,用于调整协变量 XXX 与处理 TTT 之间的关联;广义线性模型或机器学习回归器等结果建模方法,用于调整 XXX 与结果 YYY 之间的关联。
结果建模:回归
假设处理效应在协变量间恒定,或接受处理的概率在所有协变量间恒定(这两种假设均不太可能成立),则估计ATE的最简单一致方法是使用线性模型将结果对处理指示变量和协变量进行回归[9]。此时,ATE即为处理指示变量的系数。不失一般性,我们将此类结果模型(无论线性或非线性)记为 hhh:
Y^i(T)=h(Xi,T)\hat{Y}_i(T) = h(X_i, T)Y^i(T)=h(Xi,T)
在机器学习因果推断应用中广泛使用的一种更复杂的半参数结果建模方法是,利用 h(X,T)h(X, T)h(X,T) 对 Y^(1)\hat{Y}(1)Y^(1) 和 Y^(0)\hat{Y}(0)Y^(0) 进行插补,并将每个单元的CATE计算为插入估计量:
CATE^i=τ^i=Y^i(1)−Y^i(0)=h(Xi,1)−h(Xi,0)\hat{\text{CATE}}_i = \hat{\tau}_i = \hat{Y}_i(1) - \hat{Y}_i(0) = h(X_i, 1) - h(X_i, 0)CATE^i=τ^i=Y^i(1)−Y^i(0)=h(Xi,1)−h(Xi,0)
ATE的估计式为:
ATE^=1N∑i=1Nτ^i\hat{\text{ATE}} = \frac{1}{N}\sum_{i=1}^N \hat{\tau}_iATE^=N1i=1∑Nτ^i
处理建模:非参数匹配
一种常见的处理建模策略是通过匹配平衡处理组和控制组的协变量分布。匹配要求分析师选择一种距离度量,以捕捉处理单元和未处理单元在观测协变量分布上的差异(Austin, 2011)。随后可通过多种算法,为处理状态为 TTT 的单元匹配一个或多个处理状态为 1−T1-T1−T 的对应单元(Stuart, 2010)。在一对一匹配场景中,每个处理单元都有一个协变量分布完全相同的未处理对应单元,此时处理组和控制组的协变量分布完全一致。
处理建模:IPW(逆倾向得分加权)
另一种常见方法是IPW 。在IPW中,单元的权重为其接受处理的逆倾向。不失一般性,我们将倾向函数记为 π\piπ。倾向得分定义为给定协变量时接受处理的概率:
π(X,T)=P(T∣X)\pi(X, T) = P(T \mid X)π(X,T)=P(T∣X)
ATE的最简单IPW估计器为:
ATE^=1N∑i=1N[TiYiπ^(Xi,1)−(1−Ti)Yiπ^(Xi,0)](1) \hat{\text{ATE}} = \frac{1}{N}\sum_{i=1}^N \left[ \frac{T_i Y_i}{\hat{\pi}(X_i, 1)} - \frac{(1 - T_i) Y_i}{\hat{\pi}(X_i, 0)} \right] \tag{1} ATE^=N1i=1∑N[π^(Xi,1)TiYi−π^(Xi,0)(1−Ti)Yi](1)
需注意,对于任何给定单元,上述两项中仅有一项生效。此外,此处的表达式与IPW的常规表述略有不同,因为我们将 π\piπ 视为根据 TTT 的取值产生不同输出的函数(而非标量)(见框6)[10]。
IPW加权的优势在于,若倾向得分 π\piπ 设定正确,则式(1)是ATE的无偏估计器。此外,若 π\piπ 的估计具有一致性,则IPW估计器也具有一致性(Rosenbaum和Rubin, 1983;Glynn和Quinn, 2010)。
双重稳健性
由于不同模型的假设不同,将结果建模与倾向建模或匹配估计器结合以构建双重稳健估计器 的做法并不少见。例如,应用最广泛的双重稳健估计器之一是增强IPW估计器,其表达式为:
ATE^=1N∑i=1N[(Tiπ(Xi,1)−1−Tiπ(Xi,0))⏟处理建模×(Yi−h(Xi,Ti))⏟残差混杂⏟调整项+(h(Xi,1)−h(Xi,0))⏟结果建模](2) \hat{\text{ATE}} = \frac{1}{N}\sum_{i=1}^N \left[ \underbrace{\underbrace{\left( \frac{T_i}{\pi(X_i, 1)} - \frac{1 - T_i}{\pi(X_i, 0)} \right)}{\text{处理建模}} \times \underbrace{\left( Y_i - h(X_i, T_i) \right)}{\text{残差混杂}}}{\text{调整项}} + \underbrace{\left( h(X_i, 1) - h(X_i, 0) \right)}{\text{结果建模}} \right] \tag{2} ATE^=N1i=1∑N 调整项 处理建模 (π(Xi,1)Ti−π(Xi,0)1−Ti)×残差混杂 (Yi−h(Xi,Ti))+结果建模 (h(Xi,1)−h(Xi,0)) (2)
第一项是"校正后的IPW估计器"(用回归模型的残差替代原始结果),第二项是两个结果模型(分别针对处理组和控制组)的预测差值。如预期所示,若IPW估计器和回归估计器均具有一致性,则该估计器是无偏的。但更具吸引力的是,只要倾向得分 π(X,T)\pi(X,T)π(X,T) 设定正确或回归模型 hhh 估计一致,该估计器就具有一致性(Glynn和Quinn, 2010)。与单独使用任一模型(尤其是仅使用加权)相比,该模型还能提高估计效率。
双重稳健估计对于基于机器学习的因果估计尤为重要。使用简单的结果插入估计器时,偏差直接依赖于估计误差,而估计误差可能因建模策略不同而在各潜在结果间存在差异(Kennedy, 2020)。此外,基于机器学习的倾向得分估计可能严重依赖非混杂预测变量,导致出现极端权重(Schnitzer、Lok和Gruber, 2016)。更一般地,机器学习估计器无渐近线性保证,且可能收敛速度较慢,从而导致置信区间产生误导(Naimi、Mishler和Kennedy, 2021;Zivich和Breskin, 2021)。出于这些原因,若不使用双重稳健估计器,插入式机器学习估计的实证性能通常较差(Benkeser等, 2017;Kennedy, 2020;Zivich和Breskin, 2021)。
因此,机器学习因果推断文献的发展在很大程度上由半参数框架的引入所推动。半参数框架通过仅使用机器学习估计干扰参数(即潜在结果和倾向得分)来解决上述问题,这些干扰参数是ATE、CATE等因果参数的影响函数的组成部分(Chernozhukov等, 2018;Kennedy, 2016;Van der Laan和Rose, 2011)。在这类方法中,因果参数的估计仅在二阶层面依赖机器学习误差,对估计不一致具有双重稳健性,且即使机器学习模型收敛缓慢,仍能保证快速收敛和渐近有效的置信区间(Benkeser等, 2017;Kennedy, 2020;Naimi、Mishler和Kennedy, 2021;Zivich和Breskin, 2021)。下文将以最后介绍的Dragonnet算法为例,直观引入半参数理论及其在双重稳健估计中的应用(Shi、Blei和Veitch, 2019)。
我们已经厘清了因果推断的核心理论框架------从潜在结果模型下ATE与CATE的定义,到因果识别的关键假设(条件可忽略性、重叠性等),再到处理建模、结果建模及双重稳健估计器的传统策略,为后续落地深度学习做好了理论铺垫。下一部分,我们将正式进入深度因果估计的实操环节:拆解S学习器、TARNet等模型如何用神经网络实现因果推断,还会详解模型构建与参数调优的关键技巧,附上TensorFlow与PyTorch的代码演示。更多硬核实操内容,未完待续,敬请期待。

