
-- 数独求解器(基础版)
local function solve_sudoku(board)
-- 辅助函数:检查数字是否符合数独规则
local function is_valid(row, col, num)
-- 检查行是否有重复
for i = 1, 9 do
if board[row][i] == num then
return false
end
end
-- 检查列是否有重复
for i = 1, 9 do
if board[i][col] == num then
return false
end
end
-- 检查3x3宫格是否有重复
local start_row, start_col = math.floor((row - 1) / 3) * 3 + 1, math.floor((col - 1) / 3) * 3 + 1
for i = 0, 2 do
for j = 0, 2 do
if board[start_row + i][start_col + j] == num then
return false
end
end
end
return true
end
-- 辅助函数:递归回溯求解
local function backtrack(row, col)
-- 到达行尾,换行
if col > 9 then
row = row + 1
col = 1
end
-- 所有格子填完,返回成功
if row > 9 then
return true
end
-- 当前格子已有数字,跳过
if board[row][col] ~= 0 then
return backtrack(row, col + 1)
end
-- 尝试填充1-9
for num = 1, 9 do
if is_valid(row, col, num) then
board[row][col] = num -- 填充数字
if backtrack(row, col + 1) then -- 递归求解下一个格子
return true
end
board[row][col] = 0 -- 回溯:撤销填充
end
end
return false -- 无解
end
-- 从(1,1)开始求解
return backtrack(1, 1)
end
-- 打印数独棋盘
local function print_board(board)
local line = ""
for i = 1, 9 do
for j = 1, 9 do
line = line..board[i][j]..","
end
line =line.."\n"
end
print(line)
end
-- 示例数独(0表示空白格)
local sudoku0 = {
{8, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 3, 6, 0, 0, 0, 0, 0},
{0, 7, 0, 0, 9, 0, 2, 0, 0},
{0, 5, 0, 0, 0, 7, 0, 0, 0},
{0, 0, 0, 0, 4, 5, 7, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 3, 0},
{0, 0, 1, 0, 0, 0, 0, 6, 8},
{0, 0, 8, 5, 0, 0, 0, 1, 0},
{0, 9, 0, 0, 0, 0, 4, 0, 0}
}
local str=[=[000060450320009080000100007756000000203600000009080060000000000040000000037001020]=]
local str=[=[000001002000020030004500600007600050080090006100005800001004000070900003400030020]=]
local str0=[=[
000060450
320009080
000100007
756000000
203600000
009080060
000000000
040000000
037001020]=]
local sudoku = {}
for i=1,9 do
sudoku[i] = {}
for j=1,9 do
local k=(i-1)*9+j
sudoku[i][j]=tonumber(string.sub(str,k,k))
end
end
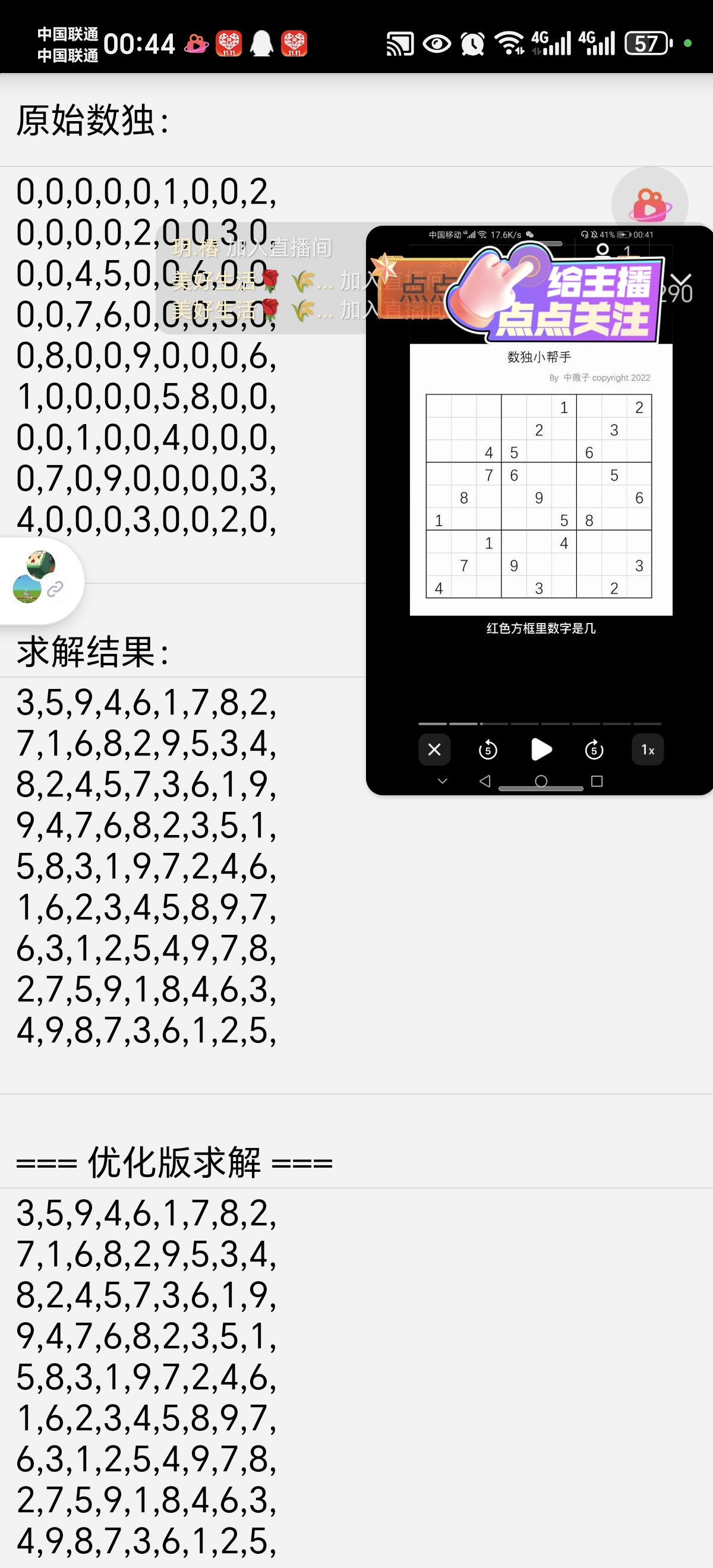
print("原始数独:")
--print(str0)
print_board(sudoku)
-- 求解数独
if solve_sudoku(sudoku) then
print("\n求解结果:")
print_board(sudoku)
else
print("无解!")
end
--[=[
代码说明:
is_valid函数:检查当前数字在行、列、3x3宫格中是否重复,符合数独规则则返回true。
backtrack函数:递归尝试填充空白格(0),若当前数字导致后续无法求解,则回溯(撤销填充)并尝试下一个数字。
print_board函数:格式化打印数独棋盘,便于查看结果。
- 优化版数独求解器(带候选数预检)
为提升效率,可预先计算每个空白格的候选数字(避免无效尝试):
--]=]
-- 数独求解器(优化版:候选数预检)
local function solve_sudoku_optimized(board)
-- 预计算每个空白格的候选数字
local candidates = {}
for i = 1, 9 do
candidates[i] = {}
for j = 1, 9 do
if board[i][j] == 0 then
candidates[i][j] = {}
for num = 1, 9 do
if is_valid(i, j, num) then
table.insert(candidates[i][j], num)
end
end
end
end
end
-- 辅助函数:递归回溯求解(使用候选数)
local function backtrack(row, col)
if col > 9 then
row, col = row + 1, 1
end
if row > 9 then
return true
end
if board[row][col] ~= 0 then
return backtrack(row, col + 1)
end
-- 获取当前格子的候选数字
local cand_list = candidates[row][col]
for _, num in ipairs(cand_list) do
board[row][col] = num
if backtrack(row, col + 1) then
return true
end
board[row][col] = 0
end
return false
end
return backtrack(1, 1)
end
-- 使用优化版求解
print("\n=== 优化版求解 ===")
if solve_sudoku_optimized(sudoku) then
print_board(sudoku)
else
print("无解!")
end
--[=[
关键点总结
回溯算法:通过递归尝试所有可能的数字,遇到冲突时回溯,是解决数独的经典方法。
规则检查:is_valid函数确保填充数字符合数独的行、列、宫格不重复规则。
优化策略:候选数预检可减少无效尝试,提升求解效率(尤其适用于高难度数独)。
--]=]