第四章决策树

决策树的核心思想是递归地选择最优特征对数据集进行划分，直到满足停止条件。整个过程可以概括为以下流程图：

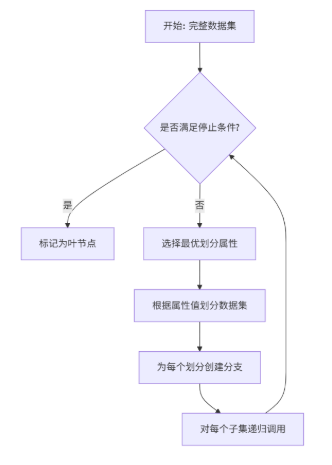
1. 决策树的生长：划分选择准则

这是决策树学习的核心，决定了树的形状和性能。

1.1 信息熵 - 纯度的度量

信息熵 是度量样本集合不确定性（纯度） 的最常用指标。熵越大，数据集越混乱。

1.2 信息增益 - ID3算法

信息增益表示使用某个属性 α 进行划分后，不确定性减少的程度。增益越大，意味着用该属性划分后"纯度提升"越大。

ID3决策树就是使用信息增益为准则来选择划分属性：

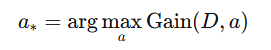
缺点：信息增益准则对可取值数目较多的属性有偏好（如"编号"属性，每个样本一个值，划分后每个子集纯度极高，信息增益最大，但这样的树没有泛化能力）。

通俗的说：

它无法区分一个特征是抓住了有意义的普遍规律 （如学习时长），还是仅仅通过唯一标识符把数据切分到最细的粒度（如学号、身份证号、编号）。

因为它盲目地崇拜"纯度"，所以会偏爱那些能把数据切得非常碎、每个子集内部极其"纯净"的特征，即使这些特征对于预测新数据毫无用处。

因此，我们需要更聪明的标准（如增益率）来惩罚那些取值过多的特征，防止决策树走上"死记硬背"的歪路。

1.3 增益率 - C4.5算法

为了克服信息增益的缺点，C4.5算法使用增益率：

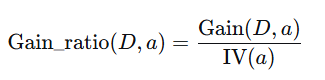
1.4 基尼指数 - CART算法

基尼值 度量了从数据集 D 中随机抽取两个样本，其类别标记不一致的概率。基尼值越小，数据集的纯度越高。

2. 决策树的剪枝：对抗过拟合

2.1 预剪枝

在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点。

评估方法 ：使用验证集准确率是否提升来判断。

优点：

降低过拟合风险
显著减少训练和测试时间开销

缺点：

基于"贪心"本质，可能欠拟合
有些分支的当前划分不能提升性能，但后续划分可能导致性能显著提高

2.2 后剪枝

先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

优点：

欠拟合风险很小
泛化性能通常优于预剪枝

缺点：

训练时间开销比未剪枝决策树和预剪枝决策树大得多

3. 连续值与缺失值处理

3.1 连续值处理 - 二分法

问题： 像"密度"、"含糖率"这种特征，值是0.697、0.774这样的数字，不像"色泽"那样是固定的几个选项。决策树该怎么问问题呢？它没法说"密度=？"。

解决方案：二分法（找一个最佳分界线）

通俗解释： 决策树会把连续值问题，变成一个 "是不是小于某个值？" 的是非题。

具体步骤（就像找最佳切割点）：

排序： 把所有西瓜的"密度"值从小到大排序。
[0.243, 0.245, 0.343, 0.360, ..., 0.774]
找候选点： 在每两个相邻的密度值之间，取一个中间值作为"候选分界线"。
候选点 = (0.243+0.245)/2, (0.245+0.343)/2, ...
评估： 决策树会挨个尝试这些候选点，看用哪个点来问问题（比如"密度 ≤ 0.381?"）能最好地把好瓜和坏瓜分开。评判标准还是我们之前说的信息增益或基尼指数。
确定问题： 假设它发现用"密度 ≤ 0.381?"这个问题来划分，信息增益最高。那么，这个点就成了决策树上的一个判断节点。

举个例子：

新来一个瓜，密度是0.5。
决策树问："密度 ≤ 0.381?"
回答是"否"，那么这个瓜就会进入"密度 > 0.381"的分支继续判断。

核心思想： 通过二分法，决策树成功地将一个连续的"大小"概念，转化成了一个简单的"是/否"问题。

3.2 缺失值处理 - 权重法

对于样本划分：

若样本在划分属性上的取值已知，则划入对应子结点，权重不变
若样本在划分属性上的取值未知，则以不同的权重划入所有子结点

问题： 现实中，数据很少是完美的。比如，某个西瓜的"根蒂"数据因为记录失误丢失了。难道就因为这一项数据缺失，我们就要扔掉整个西瓜吗？这太浪费了！

解决方案：权重分配法（让一个西瓜"分身"）

通俗解释： 一个信息不全的西瓜，它不会只属于一个分支，而是以"不同的概率"同时属于所有分支。

这需要解决两个子问题：

问题一：如何选择划分属性？（当很多瓜都有数据缺失时）

假设我们要选择用"色泽"还是"根蒂"来划分。我们不能只看那些数据完整的瓜，也要考虑有缺失的瓜。

方法：打折比较法

决策树会先只用"色泽"完整的西瓜来计算信息增益。
然后，给这个信息增益打一个折扣。折扣力度 = （具有完整"色泽"的西瓜数量 / 总西瓜数量）。
道理很简单： 一个属性再好，如果它一大半的值都缺失了，那它的实际用处也得打个折。决策树最终会选择"打折后"信息增益最高的属性。

问题二：选好属性后，如何划分那个缺失的西瓜？

这是最巧妙的部分。假设我们选择"纹理"作为划分属性，而某个西瓜的"纹理"数据缺失了。

方法：概率分身法

我们看所有纹理完整的西瓜中，分别有多少进入了"清晰"、"稍糊"、"模糊"这三个分支。比如，15个瓜，7个进入"清晰"，5个进入"稍糊"，3个进入"模糊"。
那么，这个"纹理"缺失的西瓜，就会被看作是：
- 以 7/15 的概率属于"清晰"分支
- 以 5/15 的概率属于"稍糊"分支
- 以 3/15 的概率属于"模糊"分支
在实际操作中， 就相当于把这个西瓜复制成三份，分别带入三个分支继续计算，但每份都带有一个权重（分别是7/15, 5/15, 3/15）。

举个例子：

一个"纹理"缺失的西瓜进入决策树。
它不会像其他瓜一样只走一条路，而是同时走进了三条路，只是"身份"有点不同。
在后续的判断中，这三个"分身"会各自带着自己的权重，参与后续的信息增益计算和划分。

核心思想： 不抛弃，不放弃。通过赋予权重，决策树最大限度地利用了包含缺失值的样本所提供的信息，而不是简单地将它们丢弃。

总结

问题	核心挑战	决策树的解决方案	通俗比喻
连续值	无法直接问"等于什么"	二分法，找一个最佳分界线，变成"是否小于X"的问题	给一把尺子找最佳刻度来区分大小
缺失值	不能浪费信息不全的样本	权重分配法，让样本按概率"分身"到所有分支	一个学生偏

4. 多变量决策树

传统决策树（单变量决策树）的分类边界是轴平行的。对于复杂分类边界，需要大量分段。

多变量决策树 ：非叶结点不再是仅对某个属性，而是对属性的线性组合进行测试：

这样可以产生斜的划分边界，用更复杂的单个问题替代多个简单问题，从而简化决策树。

一句话核心思想

普通决策树每次只问一个问题，而多变量决策树学会了"综合问问题"。

想象一下，你要判断一个人是不是篮球运动员。

1. 普通决策树（单变量决策树）：死板的面试官

这个面试官只会机械地一个一个问问题，并且每个问题都有非常明确的标准：

"你的身高超过2米吗？"
- 如果是，进入下一题。
- 如果否，直接淘汰。
"你的体脂率低于10%吗？"
- 如果是，进入下一题。
- 如果否，淘汰。
"你的弹跳超过70厘米吗？"
- 如果是，录用为篮球运动员。
- 如果否，淘汰。

它的特点：

问题非常直接、单一。
判断边界是横平竖直的（比如身高正好卡在2米这个死线上）。
缺点： 非常死板！可能会错过一些身高1米98，但弹跳、速度、技术都极好的天才球员。要准确判断，就需要问非常多这种死板的问题，导致决策树非常复杂。

2. 多变量决策树：聪明的资深教练

这个教练看人不是只看单一指标，他懂得综合考量。他不会问上面那些孤立的问题，而是会问一个更综合、更专业的问题：

"你的（身高 × 0.5 + 弹跳 × 0.3 + 速度 × 0.2）的总分，超过90分吗？"

你看，这个问题的高级之处在于：

它是多个特征的组合：同时考虑了身高、弹跳和速度。
它有权重：身高最重要（权重0.5），弹跳次之（0.3），速度也有贡献（0.2）。
它产生的是"斜的"判断边界：不再是"身高必须超过2米"这种硬性规定。一个身高1米95但弹跳惊人的球员，可能和一个身高2米05但弹跳一般的球员，在这个综合评分里得到一样的分数。

它的好处：

更加灵活和符合现实：很多事物的判断本就是多种因素综合作用的结果。
决策树更简洁：原本可能需要10个"死板"问题才能判断清楚的情况，现在可能2-3个"综合"问题就解决了。
性能可能更好：尤其当数据真实的分界本来就是"斜着"的时候，多变量决策树能更好地拟合这个规律。

举个西瓜的例子

普通决策树会问：
- "密度 ≤ 0.381？"
- "含糖率 ≤ 0.126？"
多变量决策树可能会问一个更厉害的问题：
- "(0.8 × 密度) + (0.044 × 含糖率) ≤ 0.313？"

这个新问题，相当于在"密度-含糖率"的坐标图里，画了一条斜的直线来区分好瓜和坏瓜，而不是画一横一竖两条线。这条斜线往往能更优雅、更准确地把两种瓜分开。

总结

类型	提问方式	比喻	优点	缺点
普通决策树	单问题："特征A达标了吗？"	死板的面试官	规则简单，易于理解	树可能很复杂，边界死板
多变量决策树	综合问题："几个特征加权组合达标了吗？"	资深的教练	树更简洁，边界灵活，能处理复杂关系	规则不易理解，训练更复杂

所以，多变量决策树可以看作是决策树的"升级版"，它通过引入简单的线性组合，让模型拥有了更强大的表达能力，用更少的问题做出更准确的决策。

第四章 决策树