【LeetCode】92. 反转链表 II

文章目录

• [92. 反转链表 II](#92. 反转链表 II)
• • 题目描述
  • [示例 1：](#示例 1：)
  • [示例 2：](#示例 2：)
  • 提示：
  • [进阶： 你可以使用一趟扫描完成反转吗？](#进阶： 你可以使用一趟扫描完成反转吗？)
  • 解题思路
  • • 问题深度分析
    • 核心思想对比
    • 算法流程图
    • 复杂度分析
    • 关键边界与陷阱
    • 方法与代码要点（Go）
    • 测试用例设计
    • 实战技巧
  • 完整题解代码

92. 反转链表 II

题目描述

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

示例 1：

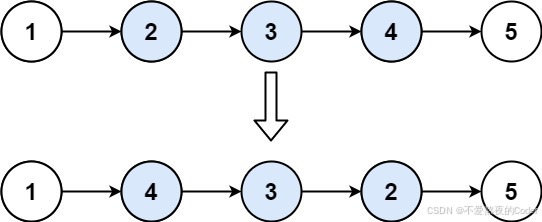
输入：head = [1,2,3,4,5], left = 2, right = 4

输出：[1,4,3,2,5]

示例 2：

输入：head = [5], left = 1, right = 1

输出：[5]

提示：

• 链表中节点数目为 n
• 1 <= n <= 500
• -500 <= Node.val <= 500
• 1 <= left <= right <= n

进阶： 你可以使用一趟扫描完成反转吗？

解题思路

问题深度分析

本题要求在单链表中仅反转[left, right]区间节点，其他部分保持原相对顺序，时间O(n)、空间O(1)的一趟扫描是最优思路。核心在于：精确定位边界、断开/接回指针、在区间内进行原地反转。

• 关键指针：pre（指向left前一个结点）、leftNode（left处结点）、rightNode（right处结点）、rightNext（right后一个结点）。
• 一趟扫描常用"头插法"在区间内原地重排；或使用常规反转再接回。

核心思想对比

• 方法一（头插法一趟扫描，最优）：固定pre，每次把leftNode后面的结点摘下，插到pre之后，实现区间内前插，O(1)空间，O(n)时间。
• 方法二（常规反转再接回）：先走到pre与rightNext，断开[left,right]，常规反转，再接回，思路直观。
• 方法三（递归：反转前N个 + 偏移）：将问题转为"反转链表前N个"子问题，向右偏移left-1次，递归优雅但实现需小心边界。
• 方法四（栈/数组辅助）：将区间内节点压栈后再弹出拼接，易写但需O(k)额外空间（k=right-left+1）。

算法流程图

主流程（以头插法为例）
哑结点dummy->head 定位pre到left前一位 leftNode=pre.next i从0到right-left-1 取出next := leftNode.next leftNode.next = next.next next.next = pre.next pre.next = next 完成, 返回dummy.next

常规反转+接回
dummy->head 找到pre与rightNode rightNext=rightNode.next 断开pre.next..rightNode子链 反转子链 pre.next=反转后的头 原leftNode.next=rightNext 返回dummy.next

递归思路（反转前N个）

graph TD A[reverseBetween(head,left,right)] --> B{left==1?} B -->|是| C[reverseN(head, right)] B -->|否| D[head.next = reverseBetween(head.next,left-1,right-1)] D --> E[返回head]

复杂度分析

• 时间复杂度：四种方法均为O(n)，n为链表长度。
• 空间复杂度：
  • 头插法与常规反转：O(1)
  • 递归：O(right-left+1) 递归栈
  • 栈法：O(right-left+1) 额外空间

关键边界与陷阱

• left==right：无需操作直接返回。
• left==1：pre为dummy，注意连接。
• 只有一个节点/空链表：直接返回。
• 区间在尾部：rightNext可能为nil，接回时谨慎。
• 指针顺序：先保存next再修改指针，避免丢链。

方法与代码要点（Go）

• 方法一：头插法一趟扫描（推荐最优）
  • 固定pre与leftNode，把leftNode后面的节点依次插到pre后面。
• 方法二：常规反转子链后接回
  • 先切出子链段，再常规反转，然后两端接回。
• 方法三：递归reverseN
  • reverseBetween(head,l,r)：若l==1，调用reverseN(head,r)；否则head.next = reverseBetween(head.next,l-1,r-1)。
• 方法四：栈辅助
  • 遍历区间压栈，随后弹栈重建区间，最后接回。

测试用例设计

• 1,2,3,4,5\], left=2, right=4 -\> \[1,4,3,2,5

• 5\], left=1, right=1 -\> \[5

• 1,2,3\], left=1, right=3 -\> \[3,2,1

• 1,2,3,4\], left=3, right=4 -\> \[1,2,4,3

• 1,2\], left=1, right=2 -\> \[2,1

• 边界：空/单节点/left==right/区间含尾部

实战技巧

• 哑结点dummy极大简化头部操作。
• 指针改动顺序：保存next -> 断开 -> 插入/反转 -> 接回。
• 模板化书写，减少出错。

完整题解代码

package main

import (
	"fmt"
)

type ListNode struct {
	Val  int
	Next *ListNode
}

// =========================== 方法一：头插法一趟扫描（最优） ===========================
func reverseBetween1(head *ListNode, left int, right int) *ListNode {
	if head == nil || left == right {
		return head
	}
	dummy := &ListNode{Next: head}
	pre := dummy
	for i := 1; i < left; i++ {
		pre = pre.Next
	}
	leftNode := pre.Next
	for i := 0; i < right-left; i++ {
		next := leftNode.Next
		leftNode.Next = next.Next
		next.Next = pre.Next
		pre.Next = next
	}
	return dummy.Next
}

// =========================== 方法二：常规反转子链后接回 ===========================
func reverseBetween2(head *ListNode, left int, right int) *ListNode {
	if head == nil || left == right {
		return head
	}
	dummy := &ListNode{Next: head}
	pre := dummy
	for i := 1; i < left; i++ {
		pre = pre.Next
	}
	rightNode := pre
	for i := 0; i < right-left+1; i++ {
		rightNode = rightNode.Next
	}
	rightNext := rightNode.Next
	// 切下子链
	leftNode := pre.Next
	rightNode.Next = nil
	// 反转子链
	revHead := reverseList(leftNode)
	// 接回
	pre.Next = revHead
	leftNode.Next = rightNext
	return dummy.Next
}

func reverseList(head *ListNode) *ListNode {
	var prev *ListNode
	for head != nil {
		next := head.Next
		head.Next = prev
		prev = head
		head = next
	}
	return prev
}

// =========================== 方法三：递归（reverseN + 偏移） ===========================
var successor *ListNode

func reverseBetween3(head *ListNode, left int, right int) *ListNode {
	if left == 1 {
		return reverseN(head, right)
	}
	head.Next = reverseBetween3(head.Next, left-1, right-1)
	return head
}

func reverseN(head *ListNode, n int) *ListNode {
	if n == 1 {
		successor = head.Next
		return head
	}
	last := reverseN(head.Next, n-1)
	head.Next.Next = head
	head.Next = successor
	return last
}

// =========================== 方法四：栈辅助 ===========================
func reverseBetween4(head *ListNode, left int, right int) *ListNode {
	if head == nil || left == right {
		return head
	}
	dummy := &ListNode{Next: head}
	pre := dummy
	for i := 1; i < left; i++ {
		pre = pre.Next
	}
	// 收集区间节点
	stack := []*ListNode{}
	node := pre.Next
	for i := left; i <= right; i++ {
		stack = append(stack, node)
		node = node.Next
	}
	rightNext := node
	// 从栈弹出重建
	for len(stack) > 0 {
		n := stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		pre.Next = n
		pre = pre.Next
	}
	pre.Next = rightNext
	return dummy.Next
}

// =========================== 工具方法与测试 ===========================
func buildList(vals []int) *ListNode {
	if len(vals) == 0 {
		return nil
	}
	head := &ListNode{Val: vals[0]}
	cur := head
	for i := 1; i < len(vals); i++ {
		cur.Next = &ListNode{Val: vals[i]}
		cur = cur.Next
	}
	return head
}

func toSlice(head *ListNode) []int {
	var res []int
	for head != nil {
		res = append(res, head.Val)
		head = head.Next
	}
	return res
}

func equalSlice(a, b []int) bool {
	if len(a) != len(b) {
		return false
	}
	for i := range a {
		if a[i] != b[i] {
			return false
		}
	}
	return true
}

func runTests(methodName string, f func(*ListNode, int, int) *ListNode) int {
	tests := []struct {
		in    []int
		l, r  int
		want  []int
		label string
	}{
		{[]int{1, 2, 3, 4, 5}, 2, 4, []int{1, 4, 3, 2, 5}, "mid range"},
		{[]int{5}, 1, 1, []int{5}, "single"},
		{[]int{1, 2, 3}, 1, 3, []int{3, 2, 1}, "all"},
		{[]int{1, 2, 3, 4}, 3, 4, []int{1, 2, 4, 3}, "tail"},
		{[]int{1, 2}, 1, 2, []int{2, 1}, "two"},
		{[]int{1, 2, 3, 4, 5}, 3, 3, []int{1, 2, 3, 4, 5}, "no-op"},
	}
	pass := 0
	for i, tc := range tests {
		head := buildList(tc.in)
		out := f(head, tc.l, tc.r)
		s := toSlice(out)
		ok := equalSlice(s, tc.want)
		status := "✅"
		if !ok {
			status = "❌"
		}
		fmt.Printf("  测试%d(%s): %s\n", i+1, tc.label, status)
		if !ok {
			fmt.Printf("    输入: %v, left=%d, right=%d\n", tc.in, tc.l, tc.r)
			fmt.Printf("    输出: %v\n", s)
			fmt.Printf("    期望: %v\n", tc.want)
		} else {
			pass++
		}
	}
	fmt.Printf("  通过: %d/%d\n\n", pass, len(tests))
	return pass
}

func main() {
	fmt.Println("=== LeetCode 92: 反转链表 II ===\n")
	methods := []struct {
		name string
		fn   func(*ListNode, int, int) *ListNode
	}{
		{"头插法一趟扫描（最优）", reverseBetween1},
		{"常规反转后接回", reverseBetween2},
		{"递归（reverseN）", reverseBetween3},
		{"栈辅助", reverseBetween4},
	}
	for _, m := range methods {
		fmt.Printf("方法：%s\n", m.name)
		runTests(m.name, m.fn)
	}
}