

🔥@晨非辰Tong: 个人主页
👀专栏:《C语言》、《数据结构与算法入门指南》
💪学习阶段:C语言、数据结构与算法初学者
⏳"人理解迭代,神理解递归。"
文章目录
引言
二叉树遍历是理解树结构操作的基础,也是算法设计核心环节。前、中与后序遍历,以不同顺序访问节点,体现了递归与迭代思想的精髓。掌握转换规律,不仅能提升对数据结构本质的理解,更能为解决复杂算法问题奠定基础。本文将通过经典题目,解析如何还原二叉树,深入剖析遍历背后的逻辑与实现方法。
获取原码》点我《!!!
知识点前瞻
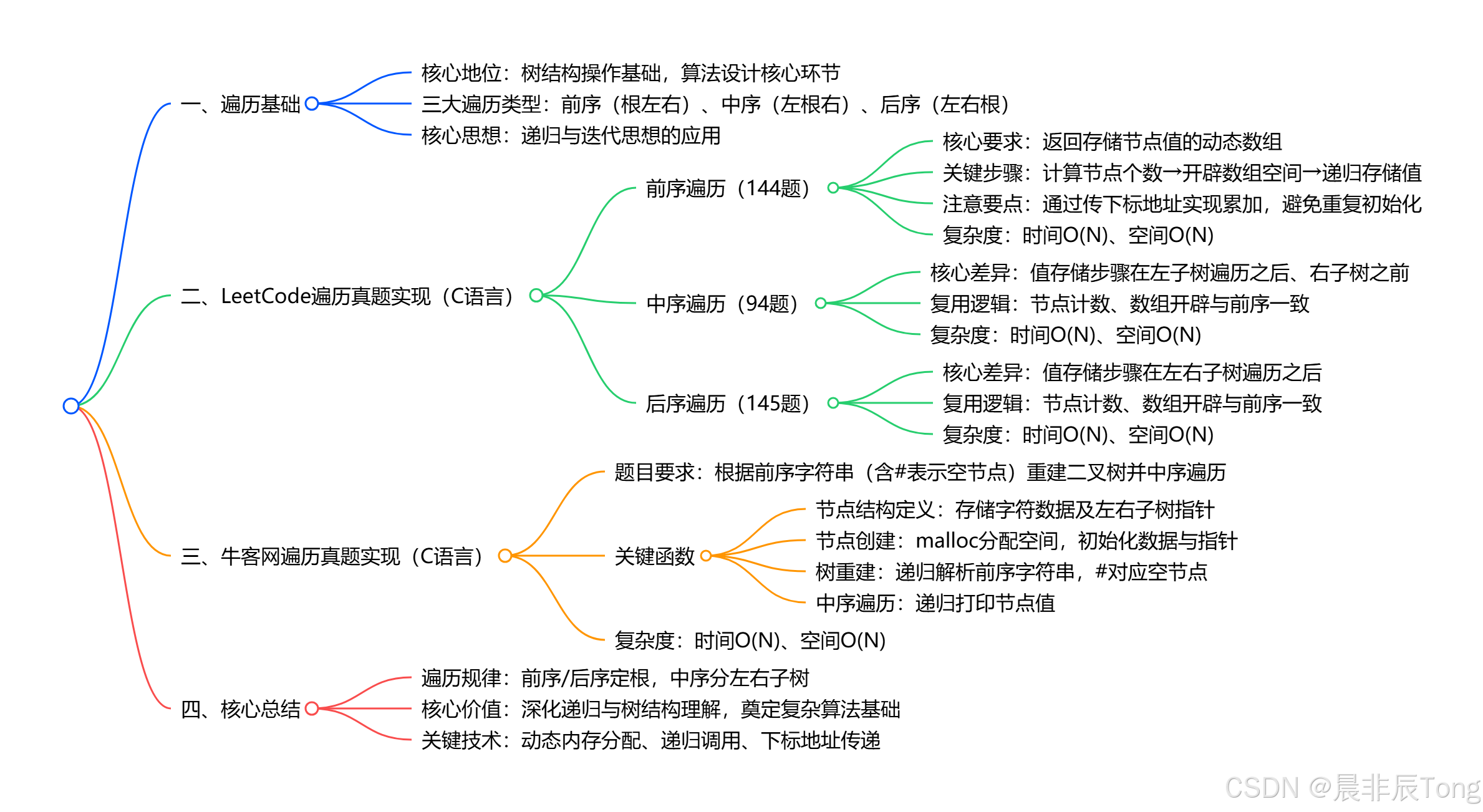
一、不一样的前序遍历
1.要求描述:

2.实现示例:
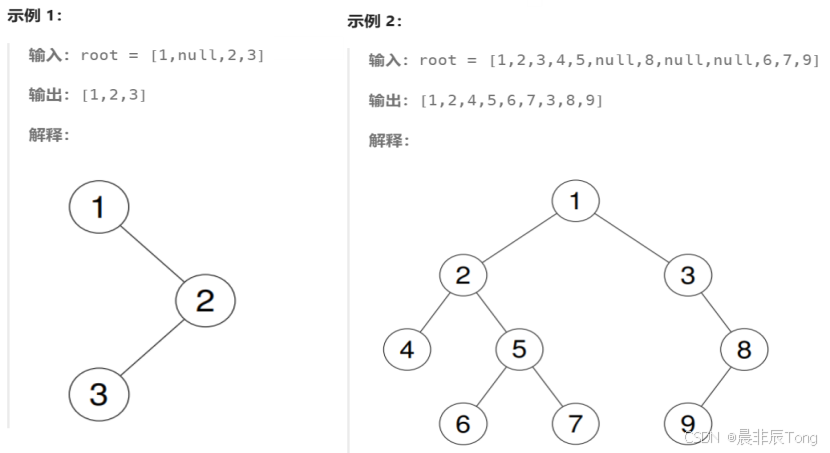
3.算法思路:
首先看平台给出的接口实现框架------>
int* preorderTraversal(struct TreeNode*root, int* returnSize),这时候再看输出示例:返回的是一个数组,那么框架应该就是来返回数组的。对于returnSize猜测是目标树的节点个数,但是输出中没有给出 ,那么要自己去实现求个数接口 。然后根据求出的节点个数去开辟数组空间(因为
Note: The returned array must be malloced, assume caller calls free().)。最后,就要实现前序遍历,但这个前序遍历与之前实现不太一样:不需要打印出节点的数值,只需要将数值存储在要返回的数组中。
复杂度:
- 时间复杂度: O(N);
- 空间复杂度: O(N);
3.1 具体代码实现
c
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//求节点个数接口
int BinaryTreeSize(struct TreeNode* root)
{
//根节点为空,树为空
if(root == NULL)
{
return 0;
}
//不为空,遍历左右子树
//实质上就是根节点个数的累加
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
//前序遍历接口
void PreOrder(struct TreeNode* root, int* arr, int* pi)
{
//空树,直接返回
if(root ==NULL)
{
return;
}
//将非空节点的值存储在要返回的数组
arr[(*pi)++] = root->val;
//遍历子树
PreOrder(root->left, arr, pi);
PreOrder(root->right, arr, pi);
}
//返回数组接口
//returnSize:树的节点个数,输入为给出,代表要自己计算
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
//调用函数求节点个数,开辟空间
*returnSize = BinaryTreeSize(root);
//开辟空间
int* arr = (int*)malloc(sizeof(int) * (*returnSize));
//前序遍历
int i = 0;
PreOrder(root, arr, &i);
return arr;
}
3.2 注意要点
- 变量
i的定义、传参 :程序中数据存放在数组中需要下标i,并没有在前序遍历接口中创建或者创建全局变量,而是通过传参(会导致i重复初始化或者累加,前面说过)。但是传的是地址 ,如果只传数值的话,在后续递归调用函数,这个i不会随着元素的增加改变.
二、不一样的中序遍历
1.要求描述:

2.实现示例

3.算法思路:
整体思路与上面的前序遍历大致相同,只需要将 arr[(*pi)++] = root->val;放在PreOrder(root->left, arr, pi); PreOrder(root->right, arr, pi);中间即可。实现左根右。
复杂度:
- 时间复杂度: O(N);
- 空间复杂度: O(N);
3.1 具体代码实现:
c
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//求节点个数接口
int BinaryTreeSize(struct TreeNode* root)
{
//根节点为空,树为空
if(root == NULL)
{
return 0;
}
//不为空,遍历左右子树
//实质上就是根节点个数的累加
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
//中序遍历
void InOrder(struct TreeNode* root, int* arr, int* pi)
{
//树为空
if(root == NULL)
{
return;
}
//树不为空
//遍历左子树
InOrder(root->left, arr, pi);
arr[(*pi)++] = root->val;
InOrder(root->right, arr, pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
//调用函数求节点个数,开辟空间
*returnSize = BinaryTreeSize(root);
//开辟空间
int* arr = (int*)malloc(sizeof(int) * (*returnSize));
//中序遍历
int i = 0;
InOrder(root, arr, &i);
return arr;
}三、不一样的后序遍历
1.要求描述:

2.实现示例:
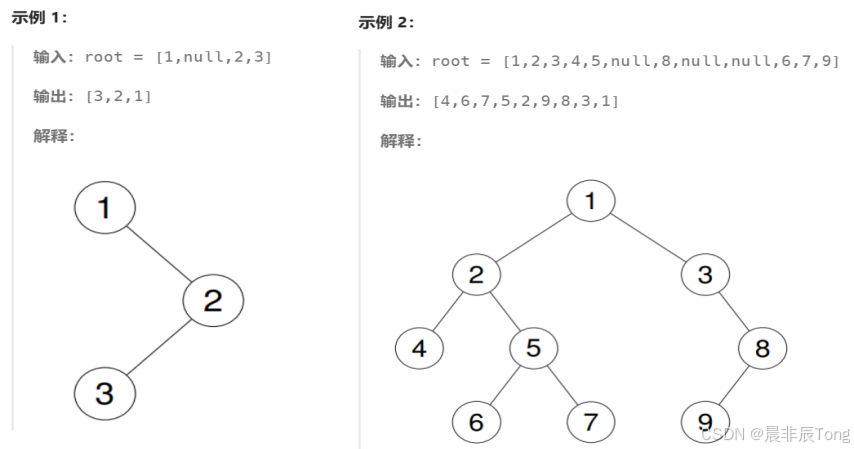
3.算法思路:
整体思路与上面的中序遍历大致相同,只需要将 arr[(*pi)++] = root->val;放在PreOrder(root->left, arr, pi); PreOrder(root->right, arr, pi);后面即可。实现左右根。
复杂度:
- 时间复杂度: O(N);
- 空间复杂度: O(N);
3.1 具体代码实现:
c
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
//求节点个数接口
int BinaryTreeSize(struct TreeNode* root)
{
//根节点为空,树为空
if(root == NULL)
{
return 0;
}
//不为空,遍历左右子树
//实质上就是根节点个数的累加
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
//后序遍历
void PostOrder(struct TreeNode* root, int* arr, int* pi)
{
//树为空
if(root == NULL)
{
return;
}
//树不为空
//遍历左子树
PostOrder(root->left, arr, pi);
PostOrder(root->right, arr, pi);
arr[(*pi)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize)
{
//调用函数求节点个数,开辟空间
*returnSize = BinaryTreeSize(root);
//开辟空间
int* arr = (int*)malloc(sizeof(int) * (*returnSize));
//后序遍历
int i = 0;
PostOrder(root, arr, &i);
return arr;
}
四、二叉树遍历
1.要求描述:

2.实现示例:
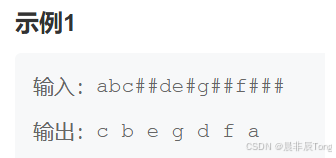
3.算法思路:
--牛客网平台全部代码都需要我们自己去实现,比较麻烦。 首先,根据描述:我们需要将用户输入的前序遍历完成的字符串存放在数组中,再根据数组来重现树的结构------>自定义创建树函数。创建树就需要知道树节点的结构,再申请节点------>定义树节点的结构、自定义创建节点函数。
上面这些函数的实现,我们前面都操作过。 然后,就是要中序遍历,这个我们也实现过。
复杂度:
- 时间复杂度:O(N) ;
- 空间复杂度:O(N);
3.1具体代码实现
c
#include <stdio.h>
#include <stdlib.h>
//定义二叉树的结构
typedef struct BinaryTreeNode
{
char data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
//根据字符创建节点
BTNode* buyNode(char ch)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
newnode->data = ch;
newnode->left = newnode->right = NULL;
return newnode;
}
//创建树
BTNode* creatTree(char* arr, int* pi)
{
//如果是空节点,返回空
if(arr[*pi] == '#')
{
(*pi)++;
return NULL;
}
//创建新节点--根左右
BTNode* root = buyNode(arr[(*pi)++]);
root->left = creatTree(arr, pi);
root->right = creatTree(arr, pi);
return root;//最终返回指向根节点的指针
}
//中序遍历
void InOrder(BTNode* root)
{
if(root == NULL)
{
return;
}
//左右根
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}
int main()
{
//读取用户输入的字符串
char arr[100];
scanf("%s", arr);
//根据字符串数组创建二叉树(前序遍历的)
int i = 0;
//接收创建树的根节点
BTNode* root = creatTree(arr, &i);
//中序遍历
InOrder(root);
return 0;
}总结
html
🍓 我是晨非辰Tong!若这篇技术干货帮你打通了学习中的卡点:
👀 【关注】跟我一起深耕技术领域,从基础到进阶,见证每一次成长
❤️ 【点赞】让优质内容被更多人看见,让知识传递更有力量
⭐ 【收藏】把核心知识点、实战技巧存好,需要时直接查、随时用
💬 【评论】分享你的经验或疑问(比如曾踩过的技术坑?),一起交流避坑
🗳️ 【投票】用你的选择助力社区内容方向,告诉大家哪个技术点最该重点拆解
技术之路难免有困惑,但同行的人会让前进更有方向~愿我们都能在自己专注的领域里,一步步靠近心中的技术目标!二叉树遍历序列的互推,核心在于把握"后序定根,中序分左右"的规律。掌握这一原理,不仅能解决序列重建问题,更能深化对递归和树结构的理解,为学习更复杂的数据结构奠定基础。