排序算法实战：从插入排序到希尔排序的实现与性能对决

云泽8082025-11-03 18:17

目录

🎬 云泽Q ：个人主页
🔥 专栏传送入口 : 《C语言》《数据结构》《C++》《Linux》

⛺️遇见安然遇见你，不负代码不负卿~

前言

大家好啊，我是云泽Q，欢迎阅读我的文章，一名热爱计算机技术的在校大学生，喜欢在课余时间做一些计算机技术的总结性文章，希望我的文章能为你解答困惑~

一、排序概念及运用

1.1 概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作

1.2 运用

购物筛选排序

院校排名

1.3 常见排序算法

以下是比较排序

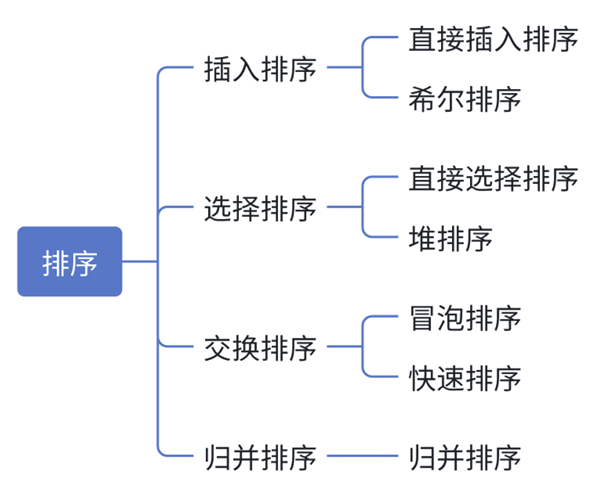
二、实现常见排序算法

c 复制代码 
int a[] = {5, 3, 9, 6, 2, 4, 7, 1, 8};

2.1 插入排序

基本思想 ：

直接插入排序是一种简单的插入排序法，其基本思想是：把待排序的记录按其关键码值得大小诸葛插入到一个已经排好序得有序序列中，直到所有得记录插入完为止，得到一个新的有序序列。

实际中我们玩扑克牌时，就用了插入排序的思想

2.1.1 直接插入排序

当插入第i（i>=1）个元素时，前面的array[0]，array[1]，...，array[i-1]已经排好序，此时用array[i]的排序码与array[i-1]，array[i-2]，...得排序码进行比较，找到插入位置即将array[i]插入，原来位置上得元素顺序后移。

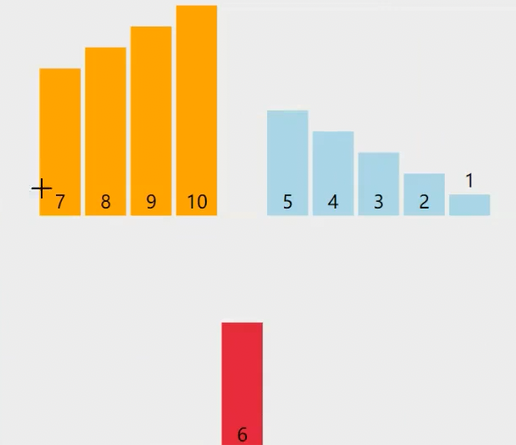
这里把6往前面插入已经排好的序列，6先与有序序列的最后一个数据10比较，若6比10小，10向后放。6继续和10前面的9比较，6比9小，9向后放，6继续和8比较，以此类推，每取到一个待排序的序列就这样一个一个的和已经排好序的序列比较

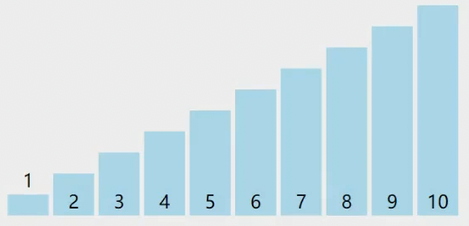
现在有一个乱序数组，将其分为排好序的记录和待排序的记录，数组中只有一个数据的时候，这个数据就是排好序的记录（这里就以3为例），剩下的就是待排序记录

首先定义一个变量end，指向已经排好序的记录中的最后一个数据，tmp指向待插入的记录

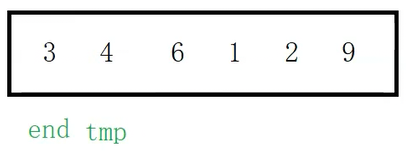
先拿tmp和end指向位置的数据比较，如果4比3小，那么4放前，3放后。这里4比3大，4就放在下标为1的位置，不用挪动

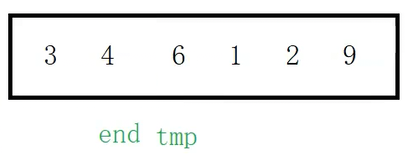
此时end加加，再次来到已经排好序的序列中的最后一个位置，tmp依旧指向待插入的记录。继续循环比较，6和end比较6大，只要待排序的记录比有序记录中的最后一个数据大，6便不用向前挪动

end接着加加，tmp来到end+1的位置，这里tmp比end小，将1保存在tmp之中，然后让end走到end+1的位置（将1覆盖）

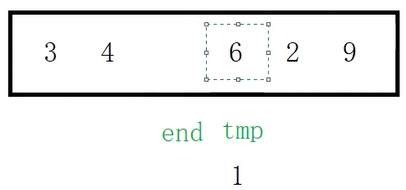
此时end减减

继续拿tmp和end比较，tmp（1）比end指向的值（4）还要小，就把end位置的值赋值给end+1的位置，end再减减

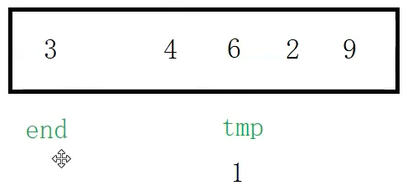
tmp继续和end指向的值比较，end的值大，把end位置的值给end+1，end再减减

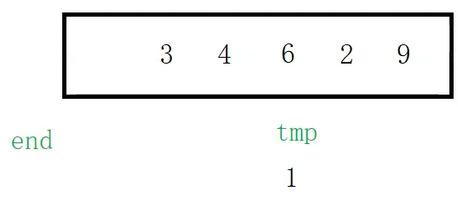
end就这样从有序序列中的最后一个记录通过减减越界了（来到下标为-1的位置），此时将tmp保存的1放到下标为0的位置，此时下标为0的位置就是end+1的位置

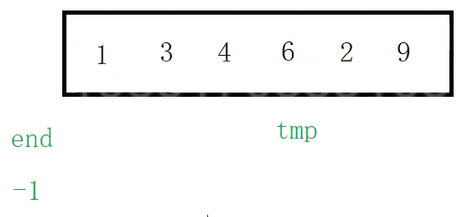
现在下一个待排序的记录是2，end继续指向有序序列中最后一个记录的位置（6）

tmp将2保存，继续拿2和end指向位置的数据比较，2和6比较，6大往后放，将end位置的数据给end+1位置，end再减减

再拿2和4比较，4大，end放到end+1的位置，end再减减来到3的位置

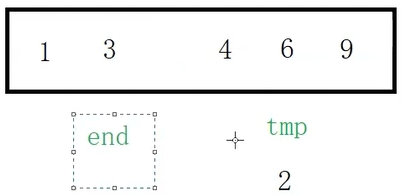
3比2大，end放到end+1的位置，end减减来到1的位置

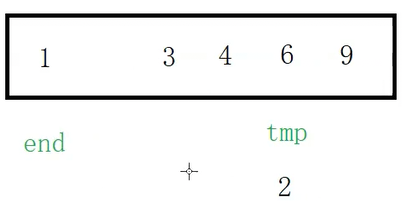
此时tmp（2）和end（1）比较，tmp大，依旧把tmp放到end+1的位置

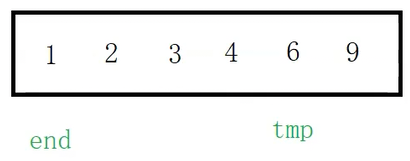
放完之后tmp向后走，end指向有序序列中的最后一个位置（6），tmp指向end的下一个位置

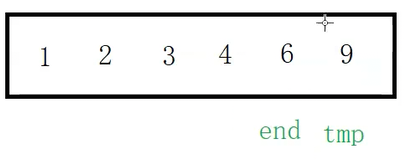
之后拿tmp和有序序列中的数据循环比较，拿tmp和end指向位置的数据比较，9比6大，这次不用将end位置的值向后覆盖，tmp位置的值依旧放到end+1的位置

以上就是直接插入排序的思想，下面是代码的实现，可以根据旁边的数组进行推导


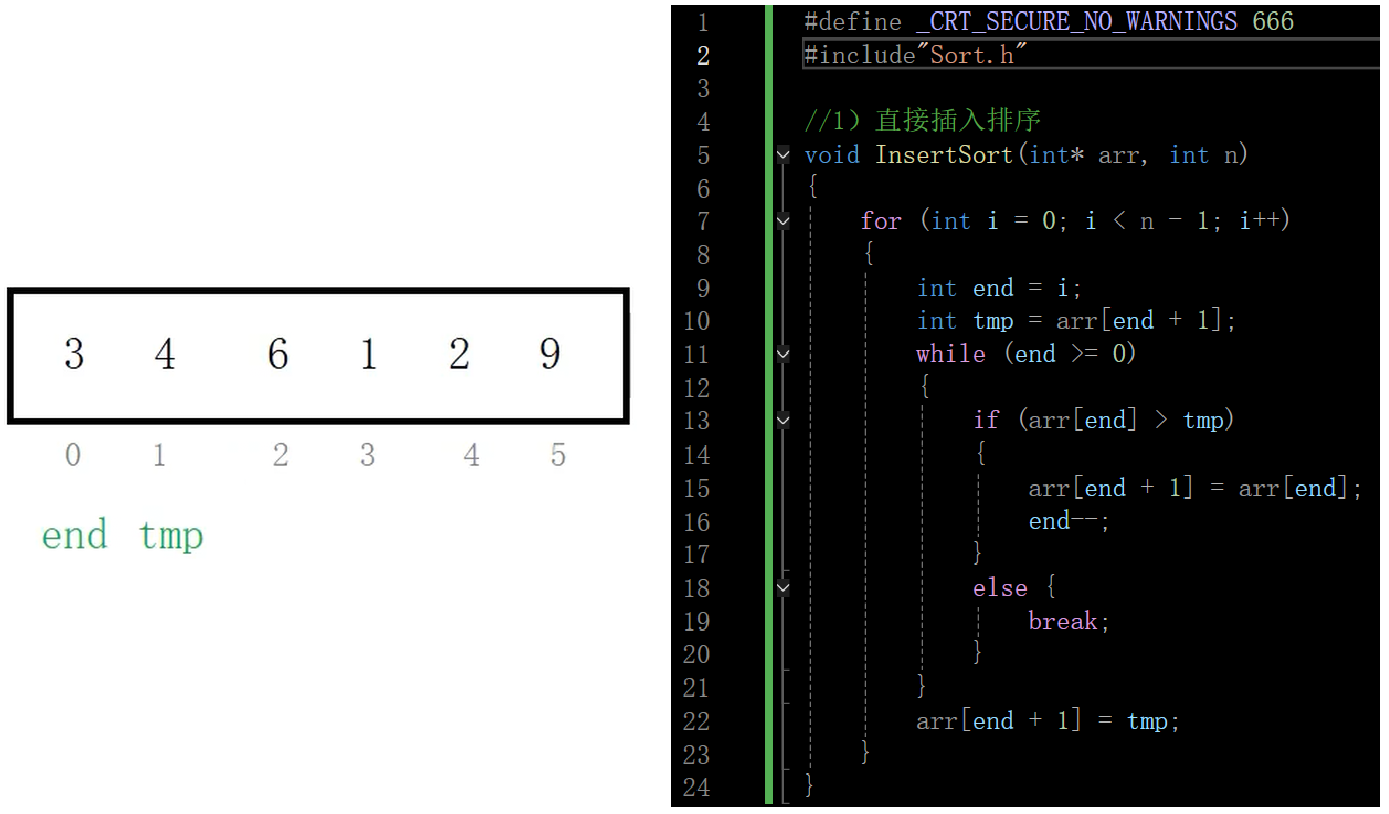
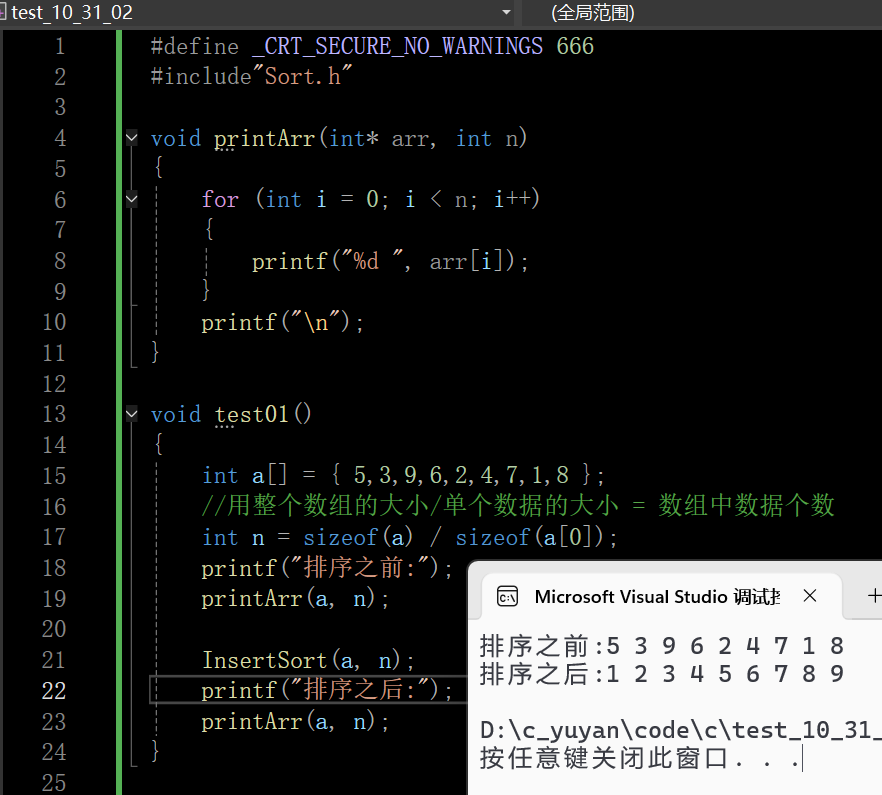
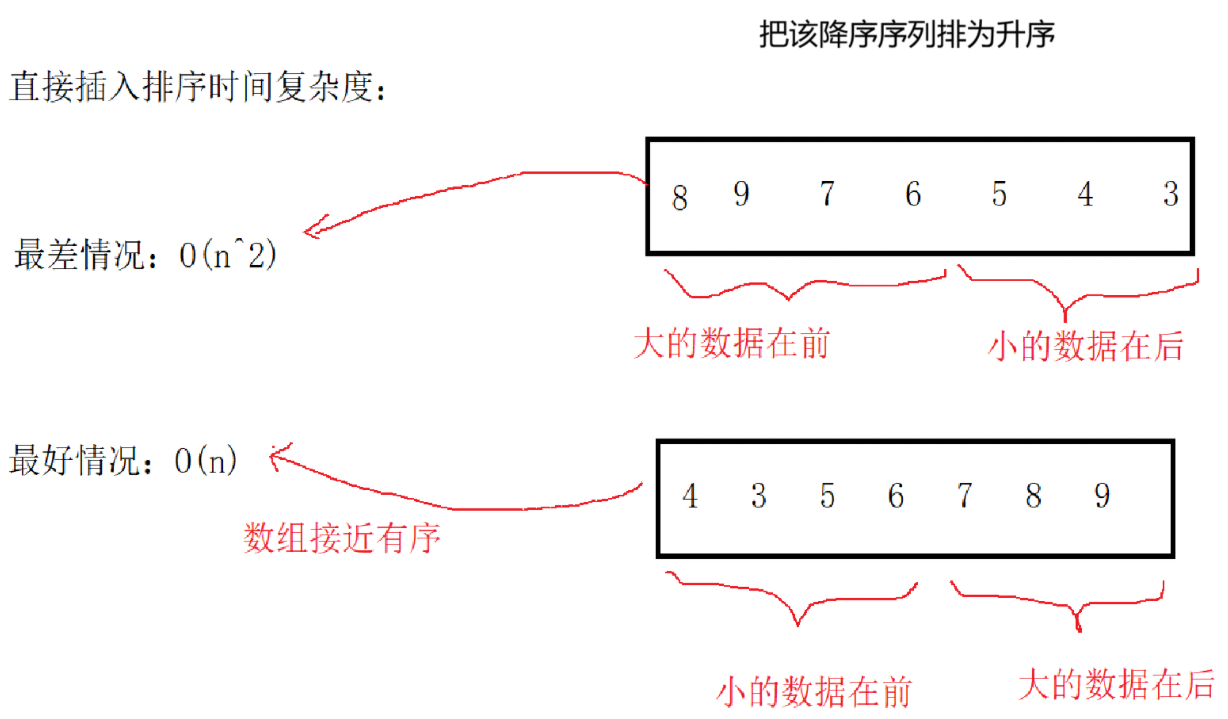
所以使用直接插入排序要根据实际情况而定，其最差的情况和冒泡排序的时间复杂度（O（n2））一样了，冒泡排序最好的情况便是数组就是有序的，不需要进行值的交换，其最好情况的时间复杂度也是O（n），不过这种情况非常少见

但是直接插入排序也不能和冒泡排序相提并论，直接插入排序是比冒泡排序要好一些的，直接插入排序最好的情况条件没有那么苛刻，只要数组接近有序就可以（小数据在前，大的数据在后）

直接插入排序的时间复杂度想要达到n2是比较困难的，很少有这种情况，即使是最差的情况也是接近n2，还有一种办法可以优化直接插入排序时间复杂度最差的情况，那就是希尔排序

2.1.2 希尔排序

希尔排序属于插入排序的一种。希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数（通常是gap = n/3+1）,把待排序文件所有记录分成各组，所有的距离相等的记录分在同一组内，并对每一组内的记录进行排序，然后gap = gap/3+1得到下一个整数，再将数组分成各组，进行插入排序，当gap=1时，就相当于直接插入排序

它是在直接插入排序算法的基础上进行改进而来的，综合来说它的效率肯定是要高于直接插入排序算法的

如图现在有一个乱序的数组，图中gap=5是指每隔5个数据为一组（第一个数据是9，第二个数据是4为一组）

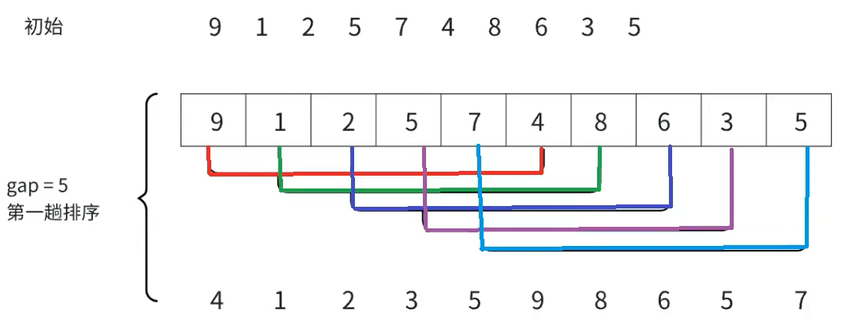
后面的组同理，每一组的数据用不同颜色的线链接，对于这样的数组，每隔gap为一组，最终划分为gap组

得到这五组之后，每一组分开排序，其中用到的排序思想都是直接插入排序

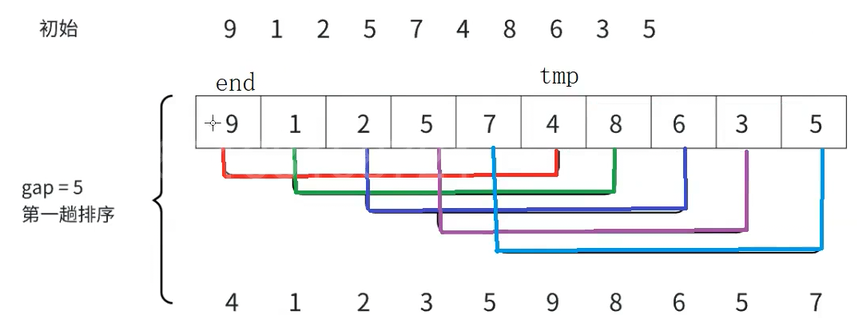
如图9和4为一组，利用直接插入排序的思想，4为tmp（待排序序列中的最后一个数据），9为end，现在把tmp往有序序列中排，此时4比9小，此时end下标为0，tmp下标为5，提前将4存起来后，将end往end+tmp位置放，之后end减减（变为-1）

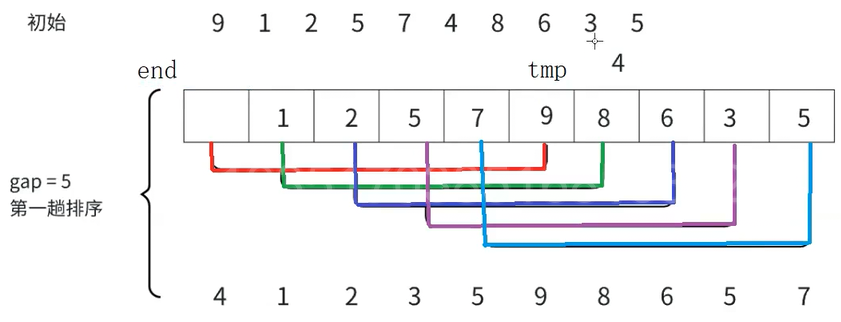
此时将4放到end+1的位置

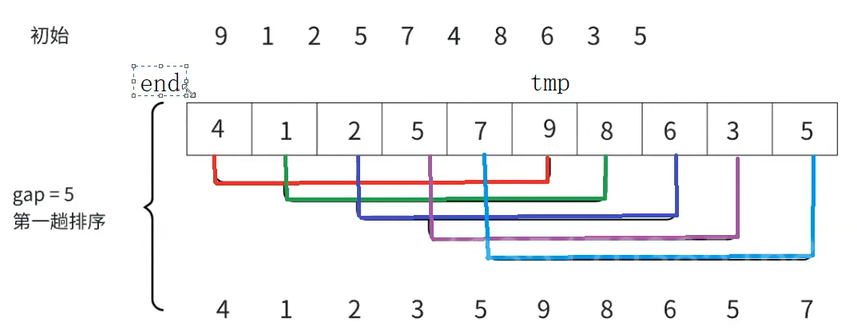
这就是直接插入排序的思想，接下来继续排，1和8，2和6都是有序的，不用交换，5和3、7和5要交换，这样就利用直接插入排序对每一次分开排序，最后得到了下面的数组

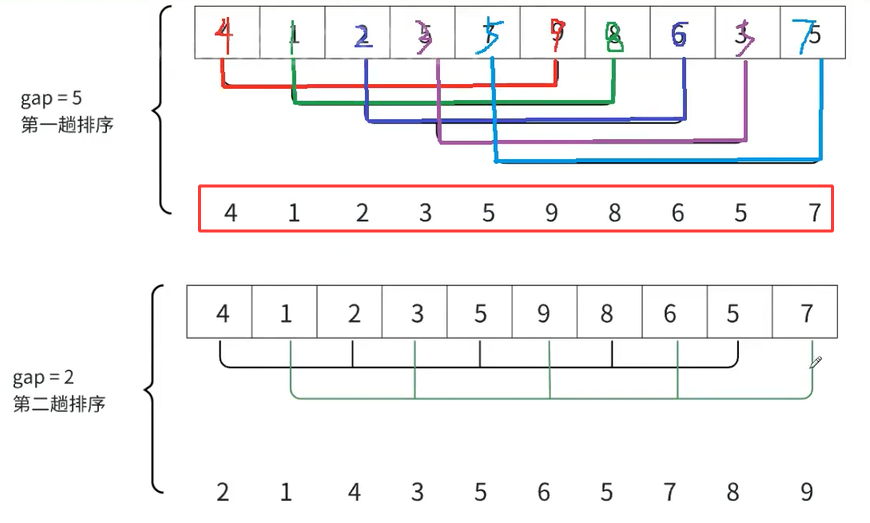
接下来继续对该数组进行划分组，gap这里 = gap / 2取整得到了2，就每隔两个数取一个值，（4，2，5，8，5）为一个大组，（1，3，9，6，7）为一个大组，每隔gap划分一组，一共会划分gap大组，这两组依旧是分开直接插入排序

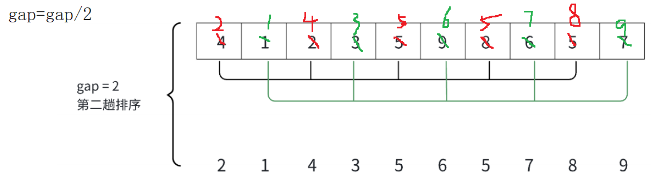
如图是第二趟分组排序的结果已经接近有序，小数据在前，大数据在后。这时候再对整个数组进行直接插入排序，时间复杂度就远远小于n2，接近O（n）

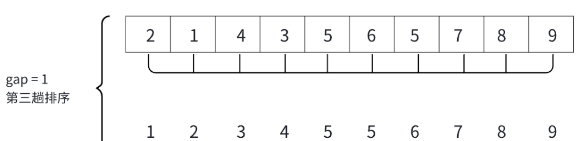
接下来对该数组进行第三趟排序，gap继续除2，每隔一个gap为一组，会划分为一组，对这一组进行直接插入排序，排完序之后会得到如图的结果

希尔排序的特性总结

  1. 当gap = 1时，就是对当前数组(已经接近有序)进行直接插入排序
  2. 当gap>1时，称为预排序，虽然数组中的数据大的在前，小的在后，但不是对其整个组进行排序，而是分为多个组进行排序，有n个数据进行while循环的时候，循环次数将达到最大，分组进行排序每组的数据量就少很多，每组进行直接插入排序时候，while循环的次数就会变少

这是一组排序的代码

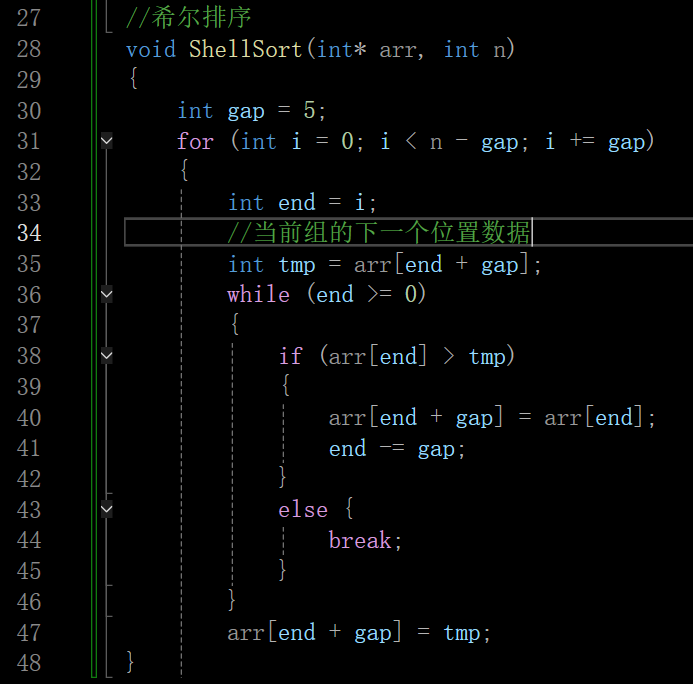
代码解释：

这里end不是减减，而是end-gap，以5和3这组为例，将end放到end+gap的位置后，end-gap（3 - 5 = -2）

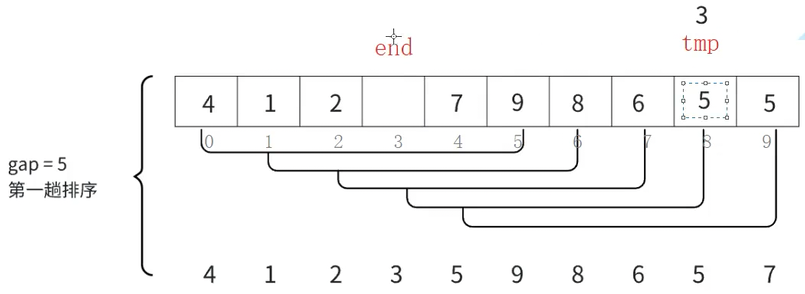
此时end就<0了，tmp放到下标为3的位置（end + gap = -2 + 5），这就是end要减gap的原因

再以gap = 2为例，将5保存在tmp中，拿tmp和end比较，end大，end放到end+gap的位置

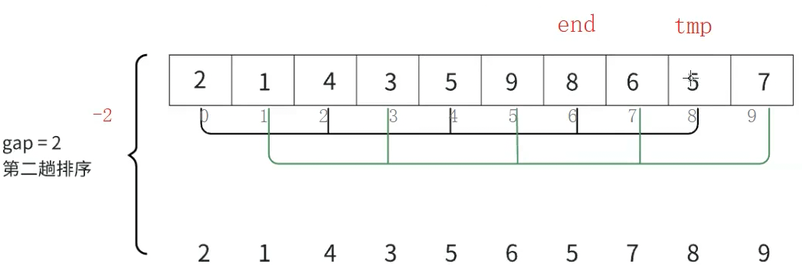
此时end再减gap，从下标为6的位置来到下标为4的位置

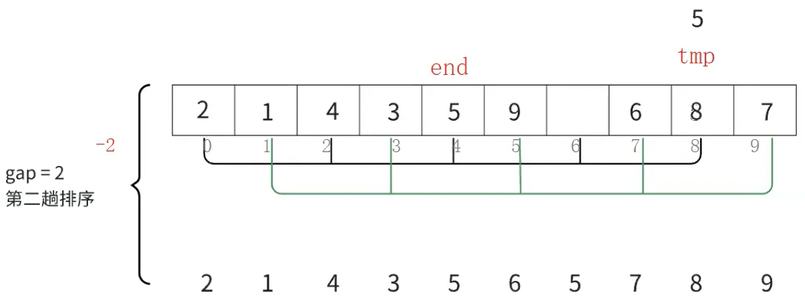
此时拿tmp和end指向位置的数值比较，5比8小就命中break条件，跳出while循环，此时tmp（5）放到end+gap的位置

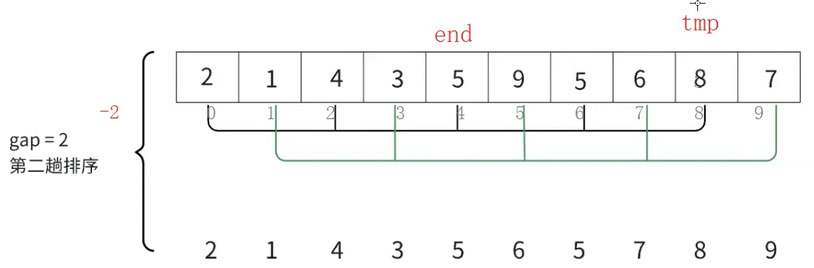
之后end要来到tmp的位置，tmp=arr[end+gap]，但是这样就越界了

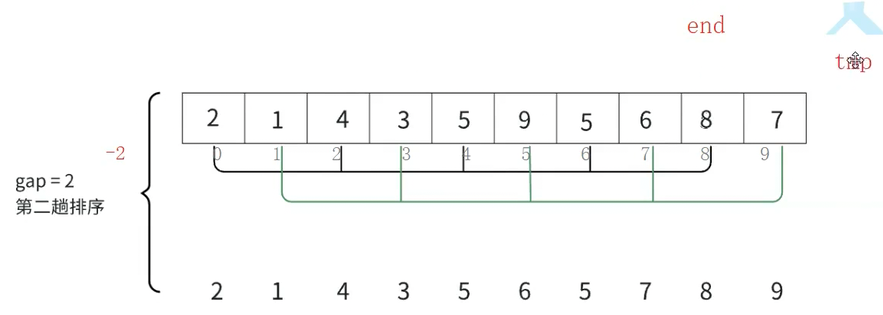
end每次从前一个位置到后一个位置隔gap步（i+=gap），现在一共有10个数据，最后一次end在下表为8的位置，这是第一组的最后一个数据，后面无数据了，不用再进入循环了，所以循环截至条件为i<n-gap

现在有gap组，所以外面还有一层循环，且例如gap=5时，有5组，每组分开进行排序，排完序之后gap还要继续除

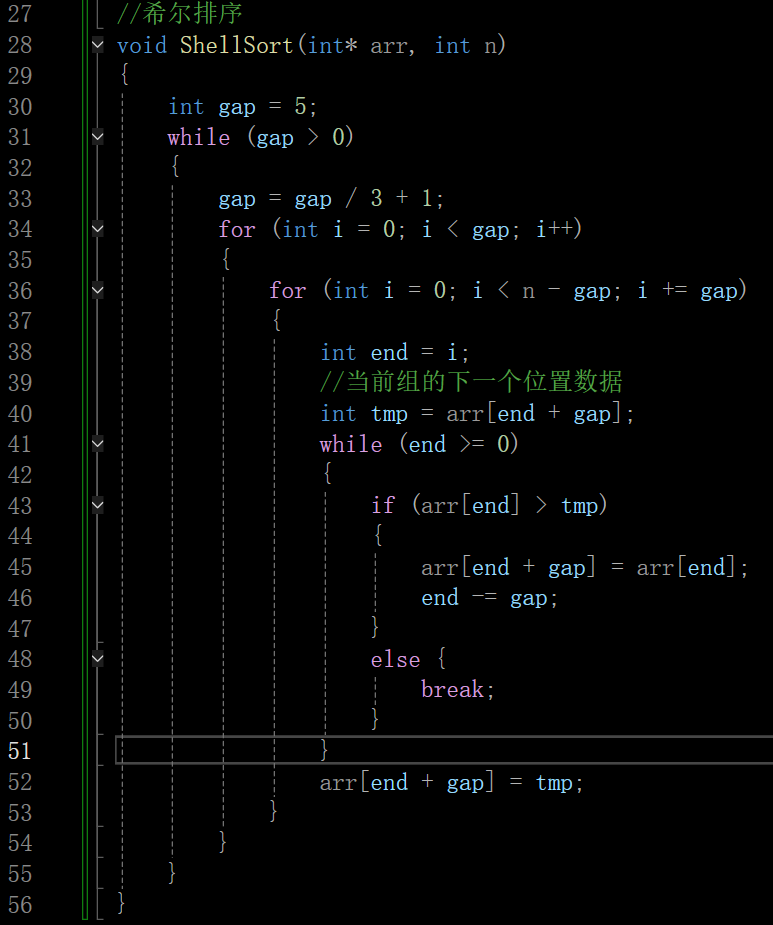
上图初始gap = n

但是这样循环就套太多了，下面还可以优化

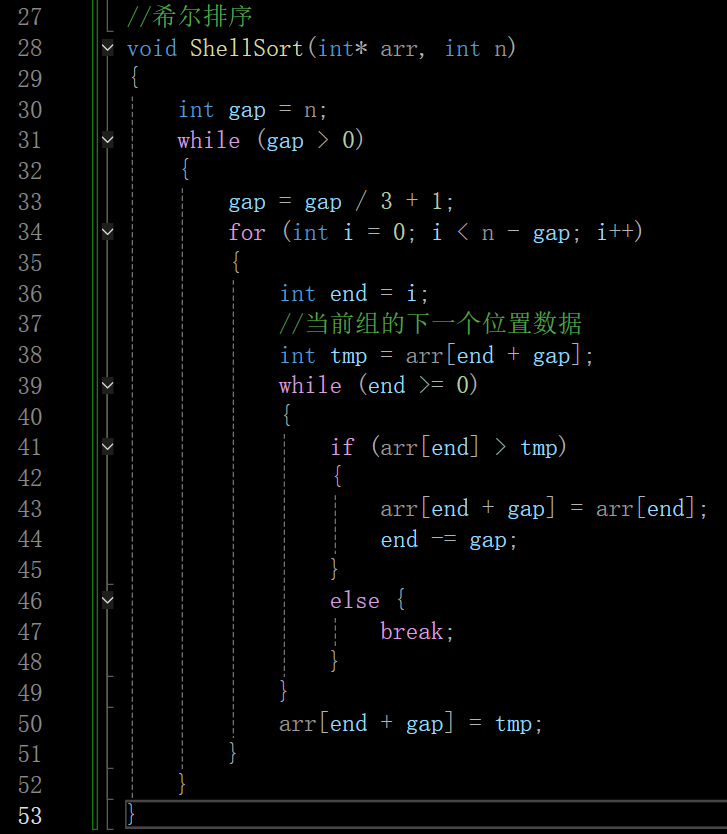
不再进行分组排序，依旧对每一组进行排序，接下来的循环就变为对第一组的第一个数据排完序后，就对第二组的1和3进行排序了，依次类推

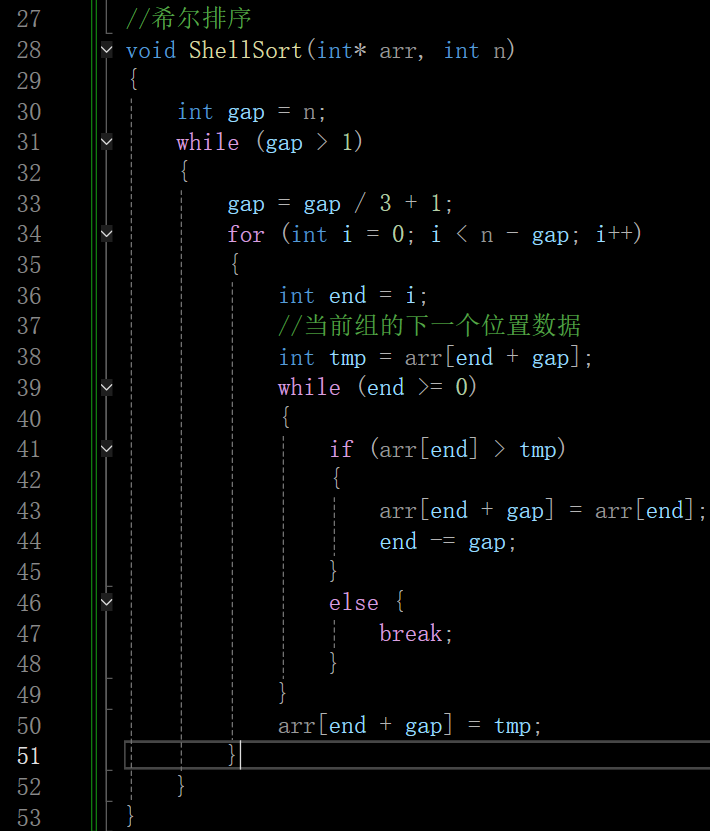
最后说一下gap的取值：

若这里gap初始值为6，且gap每次是除2，结果就是3（6除2），1（3除2），0（1除2）

若取gap/3，结果就是2，0

也就是gap/2比gap/3循环的次数更多，所以一般情况下取gap/3，+1的原因是在希尔排序中，gap最后一次必须要等于1，才能对当前数组最后进行直接插入排序，将其变为有序，若n为6时不+1，gap/3的结果就不会得到1

gap/3+1的结果就是3（第一次划分三组），2（第二次划分两组），1，也就是n为6，while循环会循环3次

基于上面的原因，希尔排序的时间复杂度推理我只写个大概，其时间复杂度为O（n1.3）即可，是优于直接插入排序的

图中坐标图是循环次数的循环次数的规律，最大的移动次数是在顶点的位置，顶点就是最终希尔排序的时间复杂度O（n1.3）。

三、测试代码：排序性能对比

接下来使用下面的代码来测试一下排序的性能对比

c 复制代码 
// 测试排序的性能对⽐
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}
	//在执行排序之前打印程序执行到此处的时间
	int begin1 = clock();
	InsertSort(a1, N);
	//在执行排序之后打印程序执行到此处的时间
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	//SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	//HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	//QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	//MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	//BubbleSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}

end1 - begin1就是该排序算法排这10w个数据所消耗的时间，这里单位是毫秒

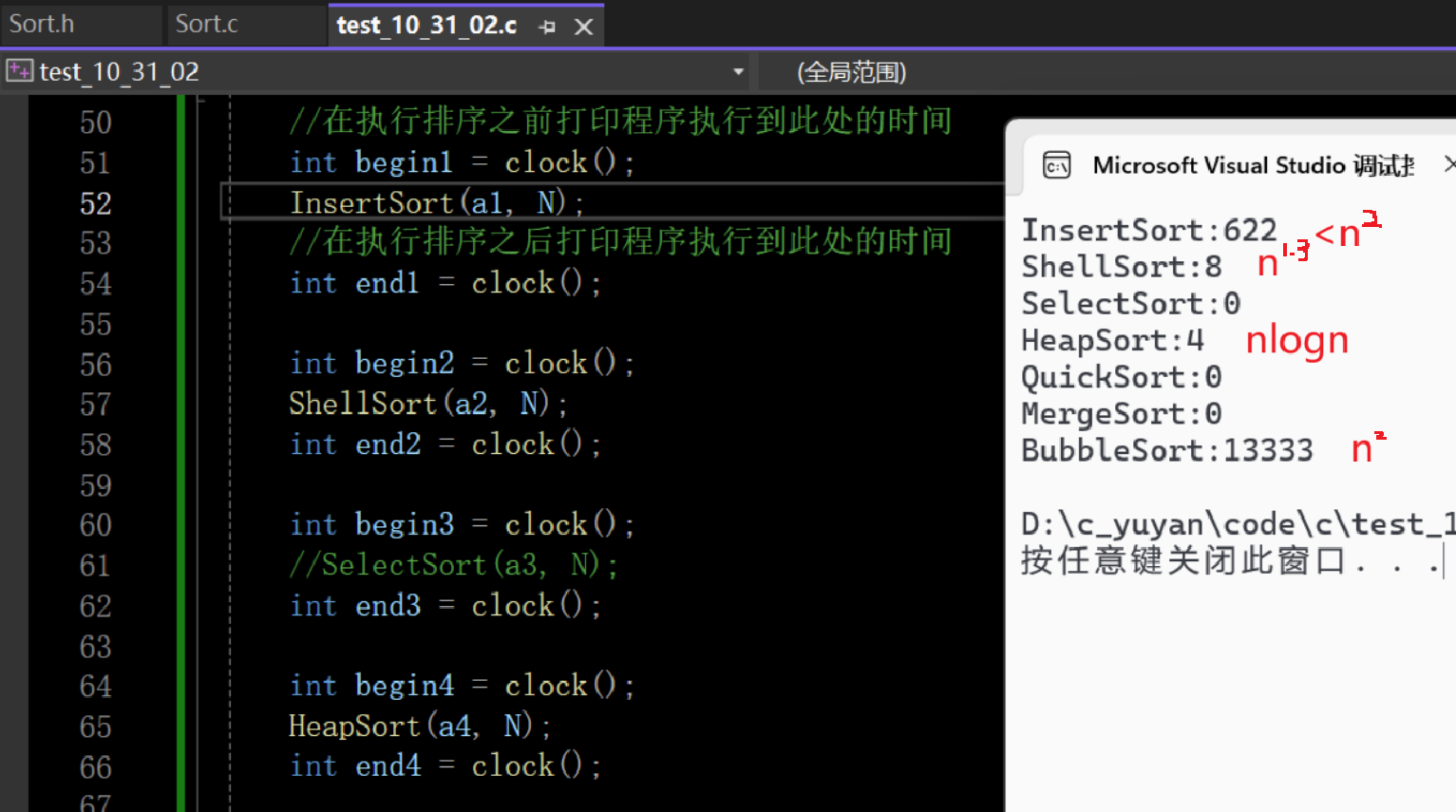
其中还有冒泡排序和堆排序的时间，不清楚代码实现的兄弟可以翻阅我数据结构和C语言专栏前面的文章

这样针对算法的效率也从时间上直接体现了出来

四、完整源码

Sort.h

c 复制代码 
#pragma once
#include<stdio.h>
#include<time.h>
#include<stdlib.h>

//插入排序
//1）直接插入排序
void InsertSort(int* arr, int n);
//2）希尔排序
void ShellSort(int* arr, int n);

//选择排序
//1）堆排序 nlogn
void HeapSort(int* arr, int n);

//交换排序
//冒泡排序 n方
void BubbleSort(int* arr, int n);

Sort.c

c 复制代码 
#define _CRT_SECURE_NO_WARNINGS 666
#include"Sort.h"

//1）直接插入排序
void InsertSort(int* arr, int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = arr[end + 1];
		while (end >= 0)
		{
			if (arr[end] > tmp)
			{
				arr[end + 1] = arr[end];
				end--;
			}
			else {
				break;
			}
		}
		arr[end + 1] = tmp;
	}
}

//希尔排序
void ShellSort(int* arr, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			//当前组的下一个位置数据
			int tmp = arr[end + gap];
			while (end >= 0)
			{
				if (arr[end] > tmp)
				{
					arr[end + gap] = arr[end];
					end -= gap;
				}
				else {
					break;
				}
			}
			arr[end + gap] = tmp;
		}
	}
}

void Swap(int* x, int* y)
{
	int tmp = *x;
	*x = *y;
	*y = tmp;
}

//向下调整算法 logn
void AdjustDown(int* arr, int parent, int n)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		//建大堆：<
		//建小堆: >
		if (child + 1 < n && arr[child] < arr[child + 1])
		{
			child++;
		}
		//孩子和父亲比较
		//建大堆：>
		//建小堆:<
		if (arr[child] > arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else {
			break;
		}
	}
}

//堆排序------------使用的是堆结构的思想 n * logn
void HeapSort(int* arr, int n)
{
	//向下调整算法------建堆n
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(arr, i, n);
	}

	////向上调整算法建堆n*logn
	//for (int i = 0; i < n; i++)
	//{
	//	AdjustUp(arr, i);
	//}

	//n*logn
	int end = n - 1;
	while (end > 0)
	{
		Swap(&arr[0], &arr[end]);
		AdjustDown(arr, 0, end);//logn
		end--;
	}
}

//冒泡排序
void BubbleSort(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n - i - 1; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				Swap(&arr[j], &arr[j + 1]);
			}
		}
	}
}

test.c

c 复制代码 
#define _CRT_SECURE_NO_WARNINGS 666
#include"Sort.h"

void printArr(int* arr, int n)
{
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

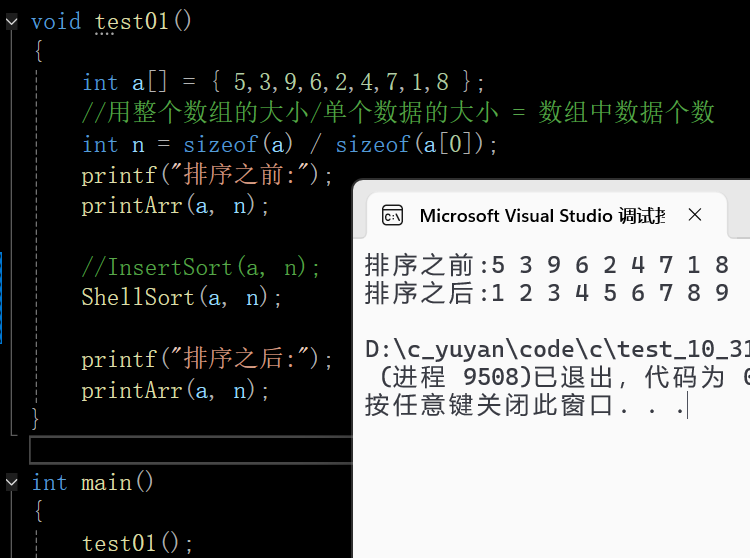
void test01()
{
	int a[] = { 5,3,9,6,2,4,7,1,8 };
	//用整个数组的大小/单个数据的大小 = 数组中数据个数
	int n = sizeof(a) / sizeof(a[0]);
	printf("排序之前:");
	printArr(a, n);

	//InsertSort(a, n);
	ShellSort(a, n);

	printf("排序之后:");
	printArr(a, n);
}

// 测试排序的性能对⽐
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}
	//在执行排序之前打印程序执行到此处的时间
	int begin1 = clock();
	InsertSort(a1, N);
	//在执行排序之后打印程序执行到此处的时间
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	//SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	//QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	//MergeSort(a6, N);
	int end6 = clock();

	int begin7 = clock();
	BubbleSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);
	printf("BubbleSort:%d\n", end7 - begin7);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}

int main()
{
	//test01();
	TestOP();
	return 0;
}

结语

相关推荐
多恩Stone8 小时前
【3DV 进阶-5】3D生成中 Inductive Bias （归纳偏置）的技术路线图
人工智能·python·算法·3d·aigc
.ZGR.9 小时前
蓝桥杯高校新生编程赛第二场题解——Java
java·算法·蓝桥杯
blammmp9 小时前
算法专题十七：穷举vs暴搜vs深搜vs回溯vs剪枝
算法·机器学习·剪枝
haofafa9 小时前
高精度加减法
java·数据结构·算法
weixin_3077791310 小时前
利用特征值和特征函数求解积分方程
算法
TT哇10 小时前
【BFS 解决FloodFill 算法】4. 被围绕的区域（medium）
算法·宽度优先
格林威10 小时前
AOI在人形机器人制造领域的应用
人工智能·数码相机·算法·目标跟踪·机器人·视觉检测·制造
小圆53111 小时前
java-learn(9):常见算法，collection框架
java·开发语言·算法
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03BongoCat - 跨平台键盘猫动画工具04《大数据技术原理与应用》实验报告三 熟悉HBase常用操作05Linux下V2Ray安装配置指南06NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南07jdk21下载、安装（Windows、Linux、macOS）08安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）09GitLab 零基础入门指南：从安装到项目管理全流程10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）