
🔥艾莉丝努力练剑:个人主页
❄专栏传送门:《C语言》、《数据结构与算法》、C/C++干货分享&学习过程记录、Linux操作系统编程详解、笔试/面试常见算法:从基础到进阶、测试开发要点全知道
⭐️为天地立心,为生民立命,为往圣继绝学,为万世开****太平
🎬艾莉丝的简介:

🎬艾莉丝的C++专栏简介:

目录
[1 ~> 初识红黑树:概念熟悉](#1 ~> 初识红黑树:概念熟悉)
[2 ~> 了解红黑树规则](#2 ~> 了解红黑树规则)
[2.1 红黑树的四条规则](#2.1 红黑树的四条规则)
[2.1.1 红黑树规则](#2.1.1 红黑树规则)
[2.1.2 结合图示,体会红黑树规则](#2.1.2 结合图示,体会红黑树规则)
[2.1.3 结合图例,理解红黑树的路径数量问题:NIL](#2.1.3 结合图例,理解红黑树的路径数量问题:NIL)
[2.2 红黑树是怎么确保最长路径不超过最短路径的2倍的?](#2.2 红黑树是怎么确保最长路径不超过最短路径的2倍的?)
[2.3 理解红黑树的效率](#2.3 理解红黑树的效率)
[3 ~> 实现红黑树](#3 ~> 实现红黑树)
[3.1 红黑树的结构实现](#3.1 红黑树的结构实现)
[3.2 红黑树的插入问题以及插入的代码实现](#3.2 红黑树的插入问题以及插入的代码实现)
[3.2.1 红黑树中插入一个值的大致过程](#3.2.1 红黑树中插入一个值的大致过程)
[3.2.2 三种情况](#3.2.2 三种情况)
[3.2.3 情况1:变色](#3.2.3 情况1:变色)
[3.2.4 情况2:单旋 + 变色](#3.2.4 情况2:单旋 + 变色)
[3.2.5 情况3:双旋 + 变色](#3.2.5 情况3:双旋 + 变色)
[3.2.6 红黑树插入的代码实现](#3.2.6 红黑树插入的代码实现)
[3.3 红黑树的旋转](#3.3 红黑树的旋转)
[3.3.1 右旋](#3.3.1 右旋)
[3.3.2 左旋](#3.3.2 左旋)
[3.3.3 左右双旋](#3.3.3 左右双旋)
[3.3.4 右左双旋](#3.3.4 右左双旋)
[3.4 红黑树的查找问题](#3.4 红黑树的查找问题)
[3.5 Size()](#3.5 Size())
[3.5.1 公共接口:不需要传root](#3.5.1 公共接口:不需要传root)
[3.5.2 私有实现:必须传root](#3.5.2 私有实现:必须传root)
[3.5.3 解决方案:双重接口设计](#3.5.3 解决方案:双重接口设计)
[3.5.3.1 公共层(面向用户)](#3.5.3.1 公共层(面向用户))
[3.5.3.2 私有层(内部递归)](#3.5.3.2 私有层(内部递归))
[3.5.4 为什么要设计成双重接口?](#3.5.4 为什么要设计成双重接口?)
[3.5.5 总结](#3.5.5 总结)
[3.5.6 Size()双重接口设计实现](#3.5.6 Size()双重接口设计实现)
[3.6 Height()](#3.6 Height())
[3.7 IsBalanceTree()](#3.7 IsBalanceTree())
[3.8 中序遍历:InOrder()](#3.8 中序遍历:InOrder())
[3.9 验证红黑树](#3.9 验证红黑树)
[3.10 红黑树的删除](#3.10 红黑树的删除)
C++的两个参考文档
老朋友(非官方文档):
官方文档(同步更新):

1 ~> 初识红黑树:概念熟悉
红黑树也是一棵二叉搜索树,其每个结点会增加一个存储位(颜色存储位),用来表示结点的颜色(两种颜色),可以是红色或者黑色(因此被称为红黑树)。通过对任何一条从根到叶子的路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因而是接近平衡的,也就是说,红黑树是近似平衡的,这里提前说一句,因为红黑树是近似平衡的,所以红黑树的插入的时间复杂度不存在最坏情况,就是O(logn),那么下面这道题就可以直接给出答案了------

2 ~> 了解红黑树规则
2.1 红黑树的四条规则
2.1.1 红黑树规则
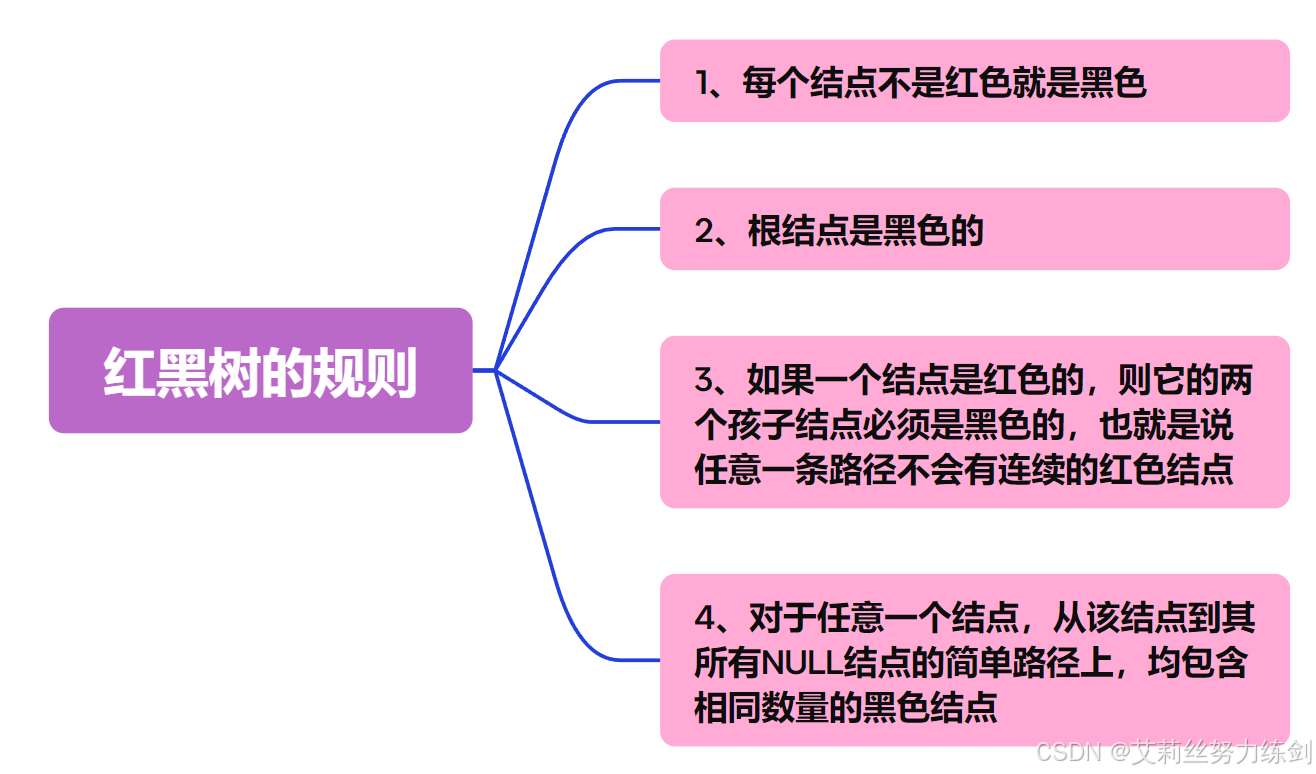
2.1.2 结合图示,体会红黑树规则
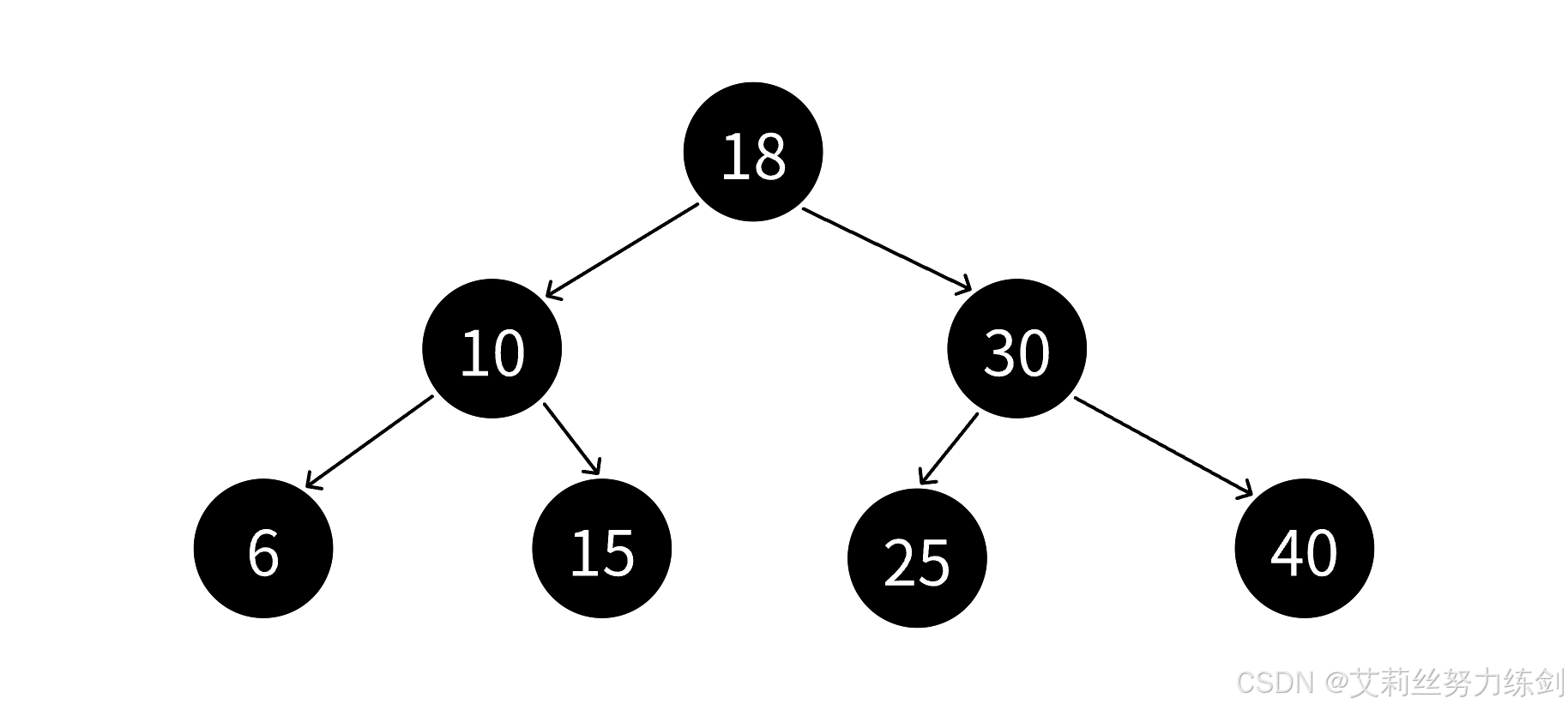
我们观察几张红黑树的图大家就能有更进一步的体会了------
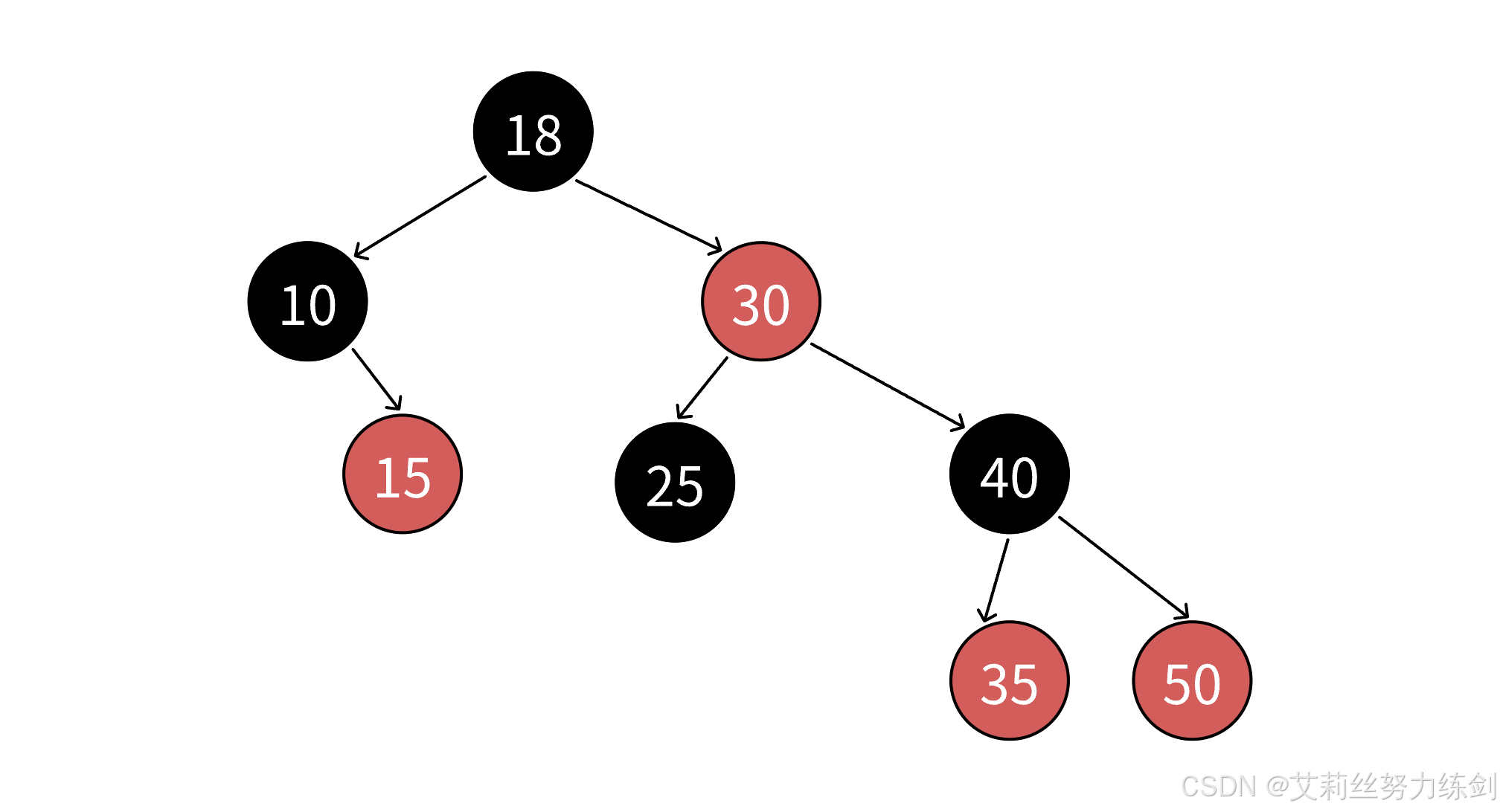
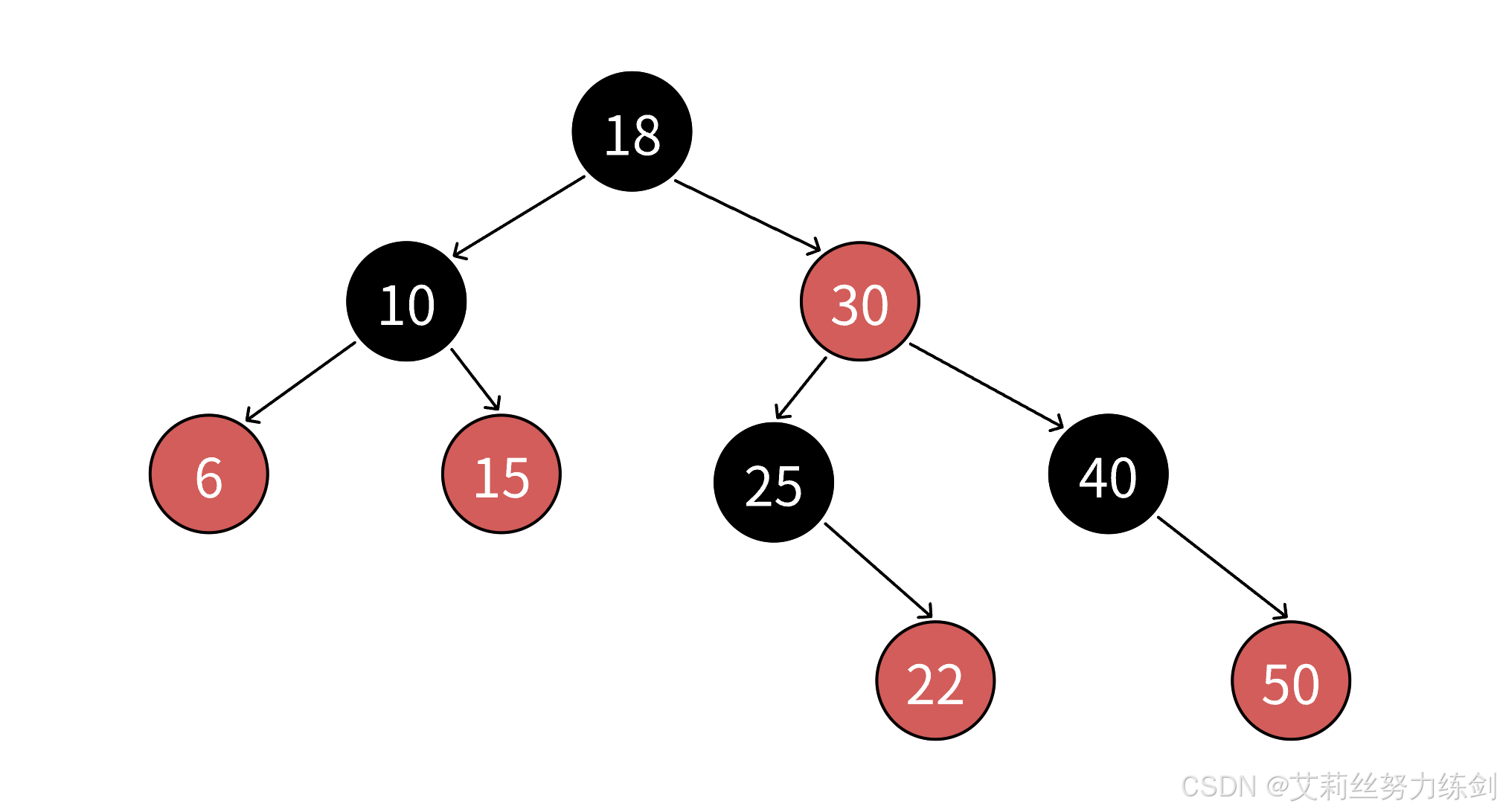
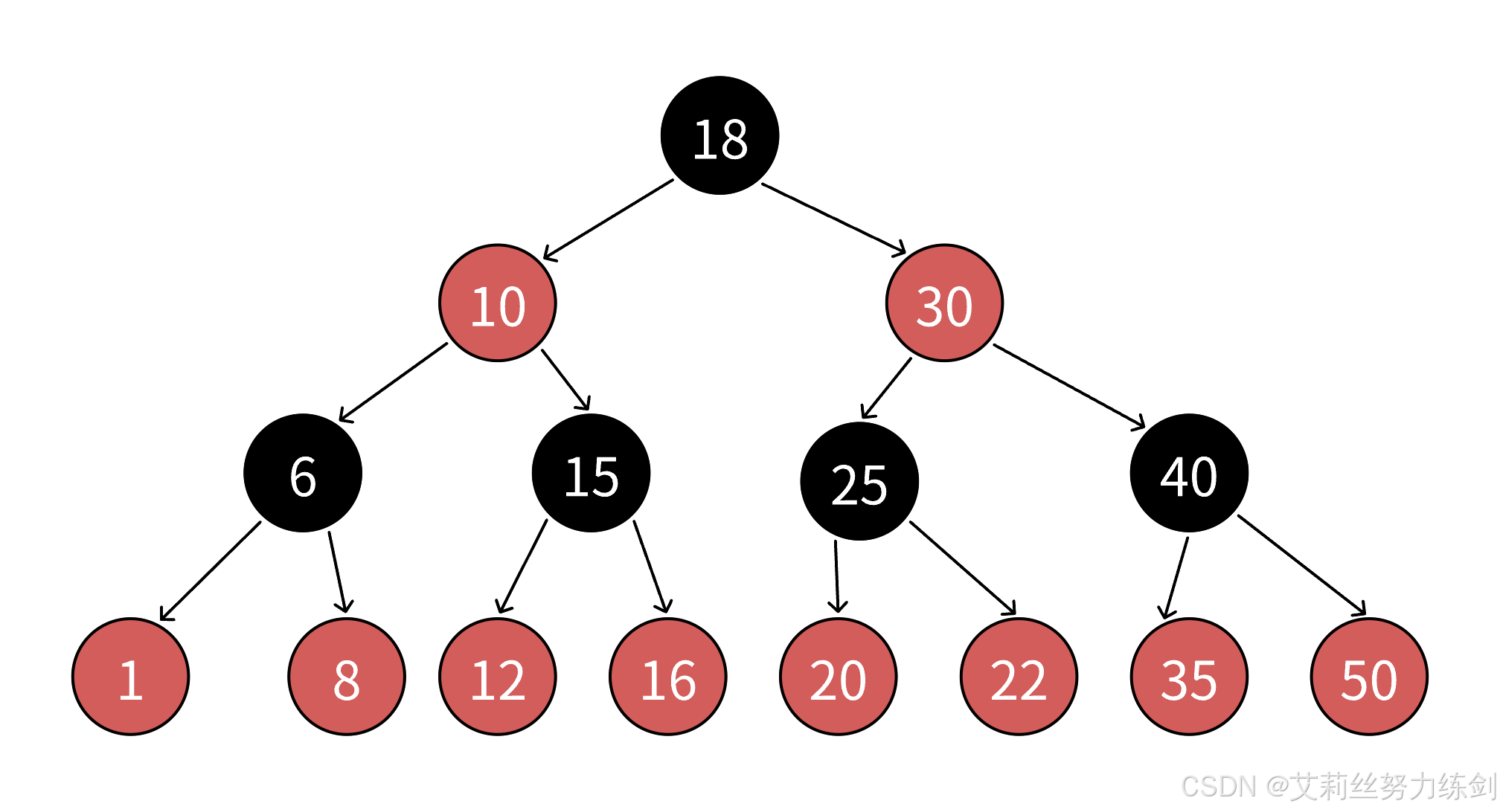
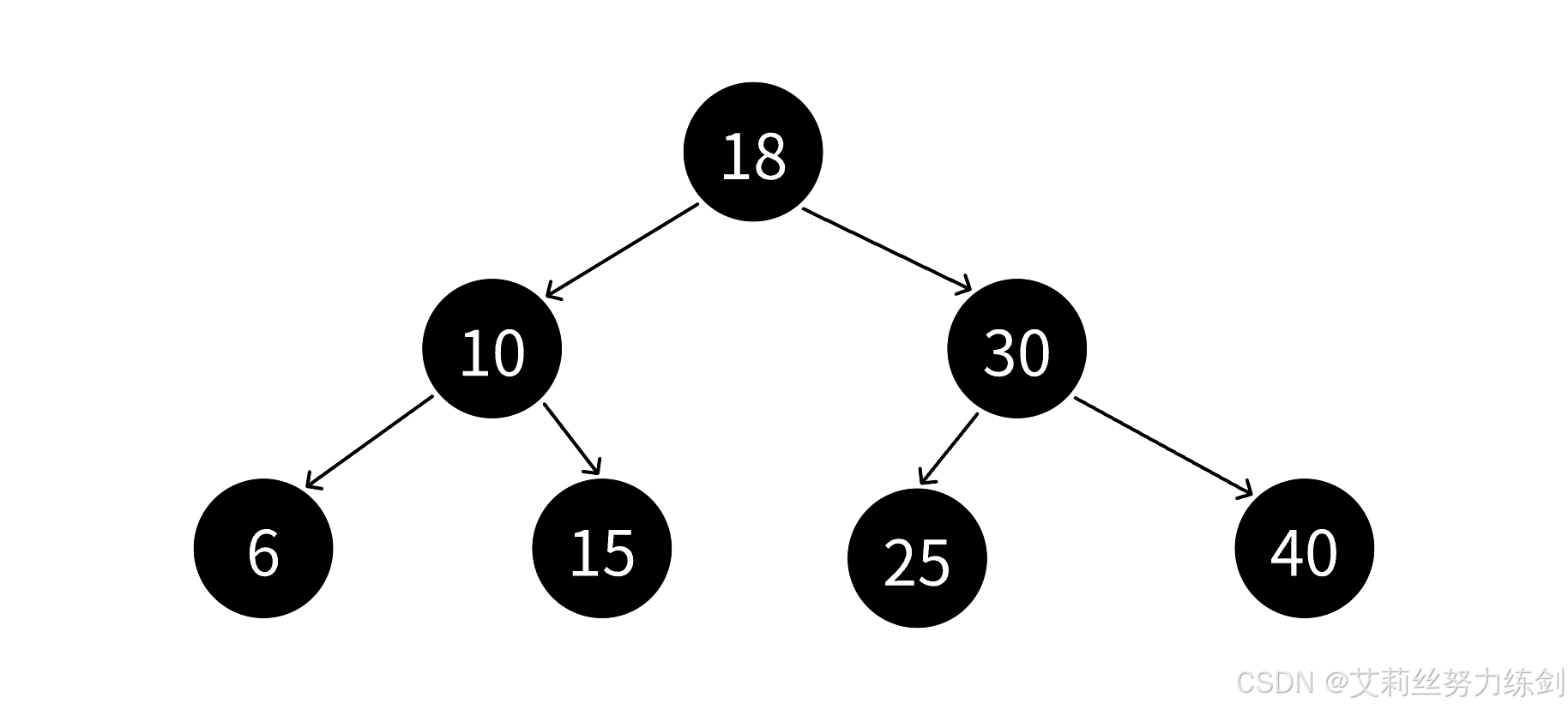
2.1.3 结合图例,理解红黑树的路径数量问题:NIL
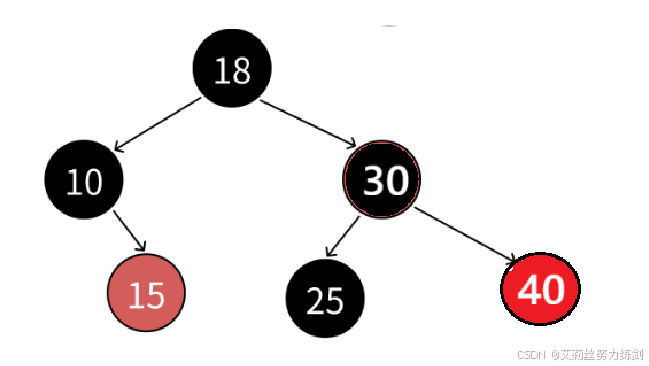
我们以上面这张图为例,艾莉丝这里考考大家,上面的红黑树里面有几条路径?
4条?不对哦!这里实际上有6条路径~~~大家请看------
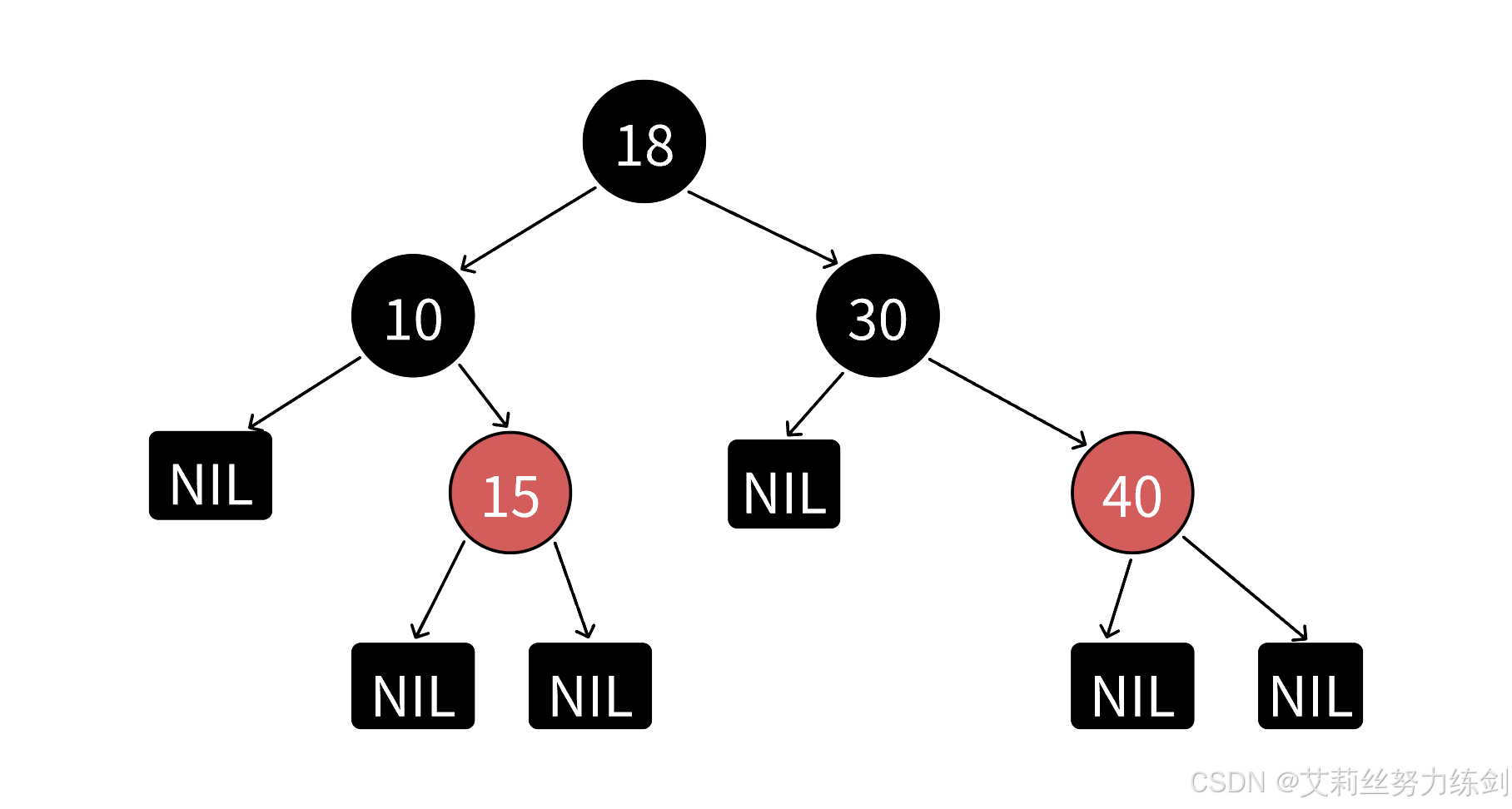
有人会问,这个NIL是啥?这个叫叶子节点,但是这个和我们二叉树里面的叶子结点不是同一个东西!这个叶子结点指的是空节点,比如上面的红色节点15,不是真正的叶子结点,它下面还有两个空节点,所以上面的黑色节点10、30还有个左孩子的NIL。
说明:《算法导论》等书籍上补充了一条每个叶子结点(NIL)都是黑色的规则。它这里所指的叶子结点不是传统的意义上的叶子结点,而是我们说的空结点,有些书籍上也把NIL叫做外部结点。NIL是为了方便准确的标识出所有路径,《算法导论》在后续讲解实现的细节中也忽略了NIL结点,所以我们知道---下这个概念即可。
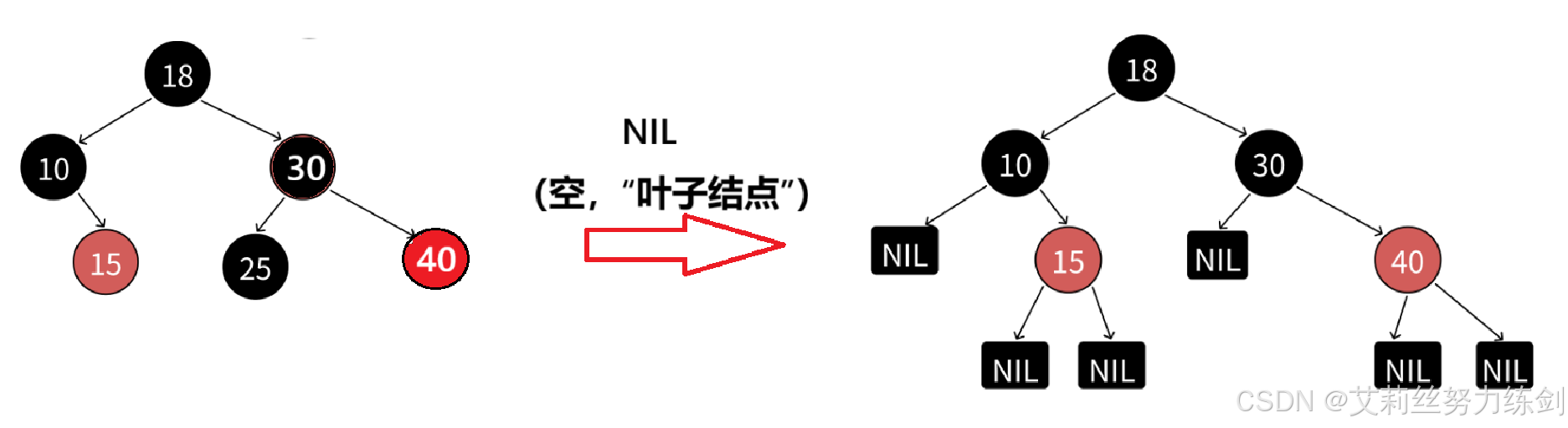
2.2 红黑树是怎么确保最长路径不超过最短路径的2倍的?
1、由规则4可知,从根到NULL结点的每条路径都有相同数量的黑色结点,所以极端场景下,最短路径就是全是黑色结点的路径,假设最短路径长度为bh(blackheight)。
2、由规则2和规则3可知,任意一条路径不会有连续的红色结点,所以极端场景下,最长的路径就是一黑一红间隔组成,那么最长路径的长度为2*bh。
3、综合红黑树的4点规则而言,理论上的全黑最短路径和一黑一红的最长路径并不是在每棵红黑树都所存在的。假设任意一条从根到NULL结点路径的长度为x,那么bh <= h <= 2*bh。
2.3 理解红黑树的效率
假设N是红黑树树中结点数量,h最短路径的长度,那么2^h - 1 <= N < 2^(2 * h) - 1,由此推出h logN,也就意味着红黑树增删查改最坏情况也就是走最长路径2*logN,那么时间复杂度还是
O(logN),像插入的情况艾莉丝在概念那里就已经给出了一个例子,这里不再赘述。

红黑树的表达相对AVL树要抽象一些,AVL树的直观在于通过高度差控制了平衡,而红黑树是通过四条规则的颜色约束来间接实现近似平衡,他们效率都是同一档次,但是相对而言,插入相同数量的结点,红黑树的旋转次数是更少的,因为红黑树对平衡的控制没那么严格,所以我们比较常用的还是红黑树,因为红黑树的旋转次数更少,效率还不比AVL树低,因此实践中红黑树用得比AVL树多,这也是红黑树相比AVL树的优势。
3 ~> 实现红黑树
3.1 红黑树的结构实现
我们用枚举值来表示一下颜色------

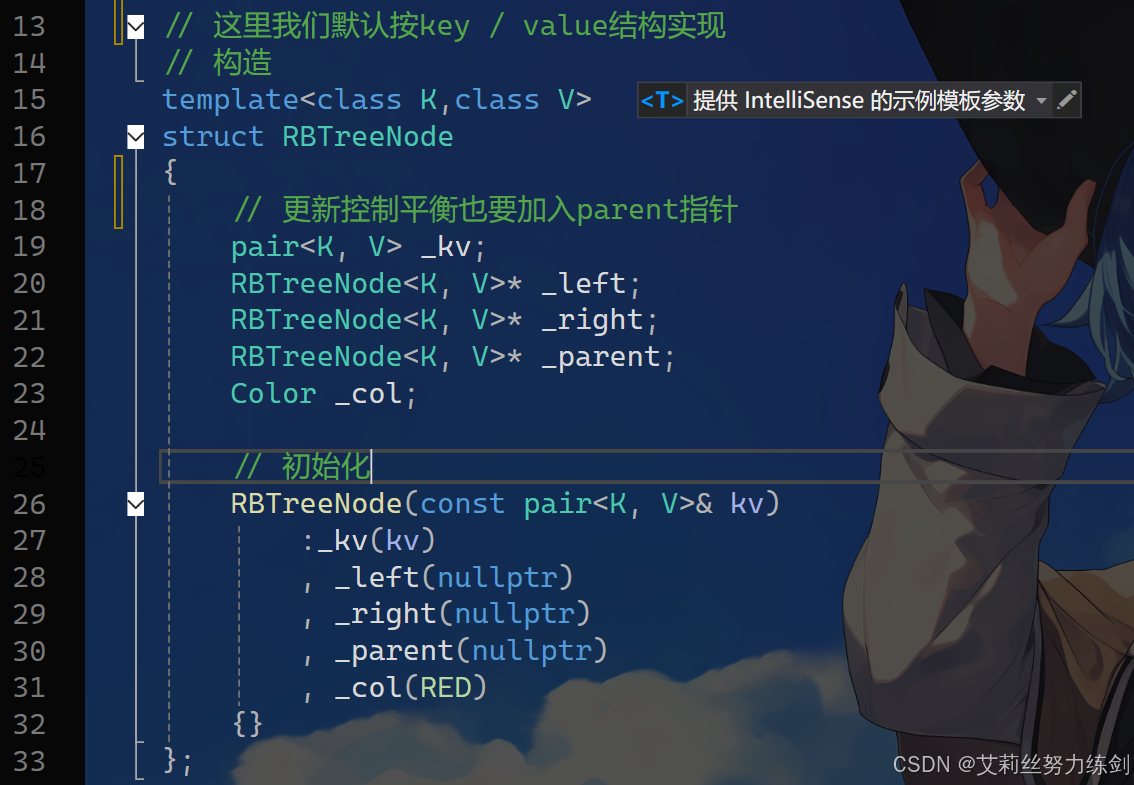
我们实现一下红黑树的结构------
3.2 红黑树的插入问题以及插入的代码实现
3.2.1 红黑树中插入一个值的大致过程

1、插入一个值按二叉搜索树规则进行插入,插入后我们只需要观察是否符合红黑树的4条规则。
2、如果是空树插入,新增结点是黑色结点。如果是非空树插入,新增结点必须红色结点,因为非空树插入,新增黑色结点就破坏了规则4,规则4是很难维护的。
3、非空树插入后,新增结点必须红色结点,如果父亲结点是黑色的,则没有违反任何规则,插入结束。
4、非空树插入后,新增结点必须红色结点,如果父亲结点是红色的,则违反规则3。进一步分析,c是红色,p为红,g必为黑,这三个颜色都固定了,关键的变化看u的情况,需要根据u分为以下几种情况分别处理。
**说明:**下图中假设我们把新增结点标识为c(cur),c的父亲标识为p(parent),p的父亲标识为g(grandfather),p的兄弟标识为u(uncle)。
3.2.2 三种情况
3.2.3 情况1:变色
c为红,p为红,g为黑,u存在且为红,则将p和u变黑,g变红。在把g当做新的c,继续往上更新。
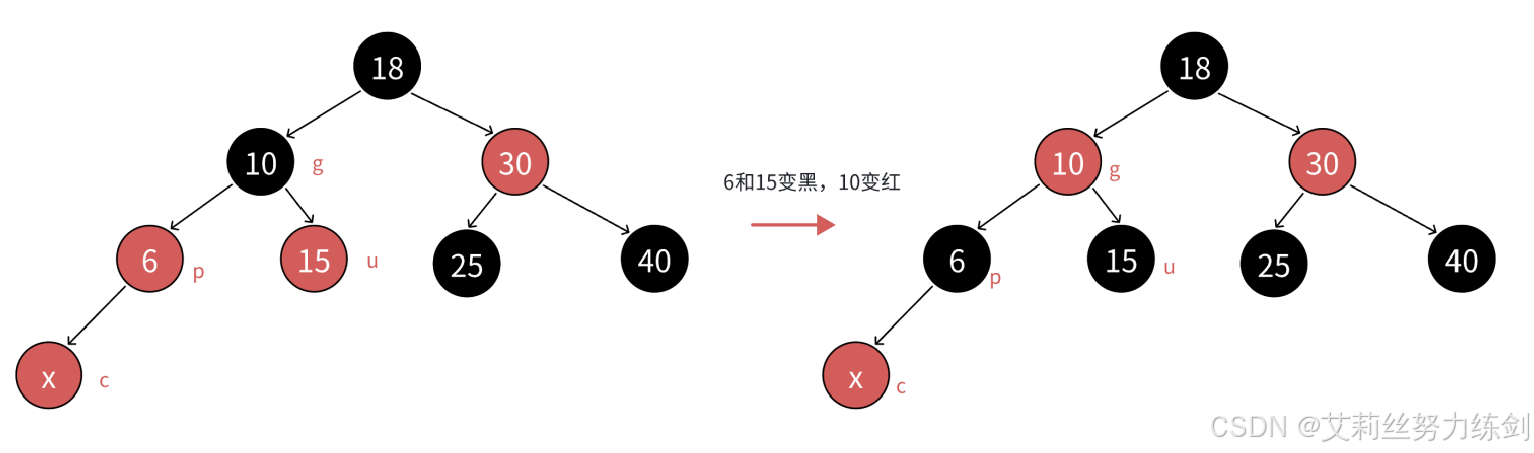
分析:因为p和u都是红色,g是黑色,把p和u变黑,左边子树路径各增加一个黑色结点,g再变红,相当于保持g所在子树的黑色结点的数量不变,同时解决了c和p连续红色结点的问题,需要继续往上更新是因为,g是红色,如果g的父亲还是红色,那么就还需要继续处理;如果g的父亲是黑色,则处理结束了;如果g就是整棵树的根,再把g变回黑色。
情况1只变色,不旋转。所以无论c是p的左还是右,p是g的左还是右,都是上面的变色处理方式。
跟AVL树类似,上图向我们展示了一种具体情况,但是实际中需要这样处理的有很多种情况。
下图将以上类似的处理进行了抽象表达,d / e / f代表每条路径拥有hb个黑色结点的子树,a / b代表每条路径拥有hb - 1个黑色结点的根为红的子树,hb >= 0。
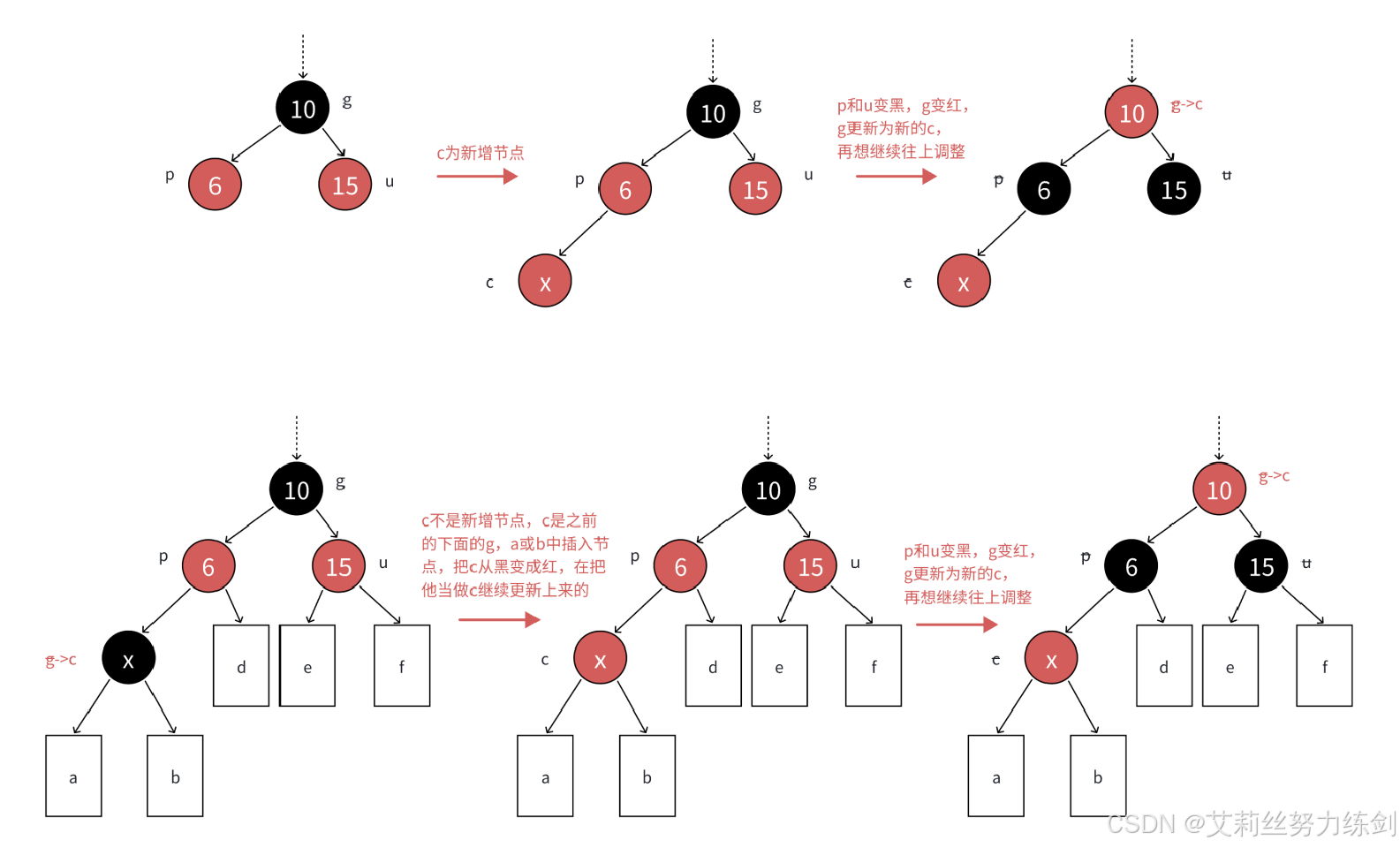
下图则分别展示了hb == 0 / hb == 1 / hb == 2的具体情况组合分析------
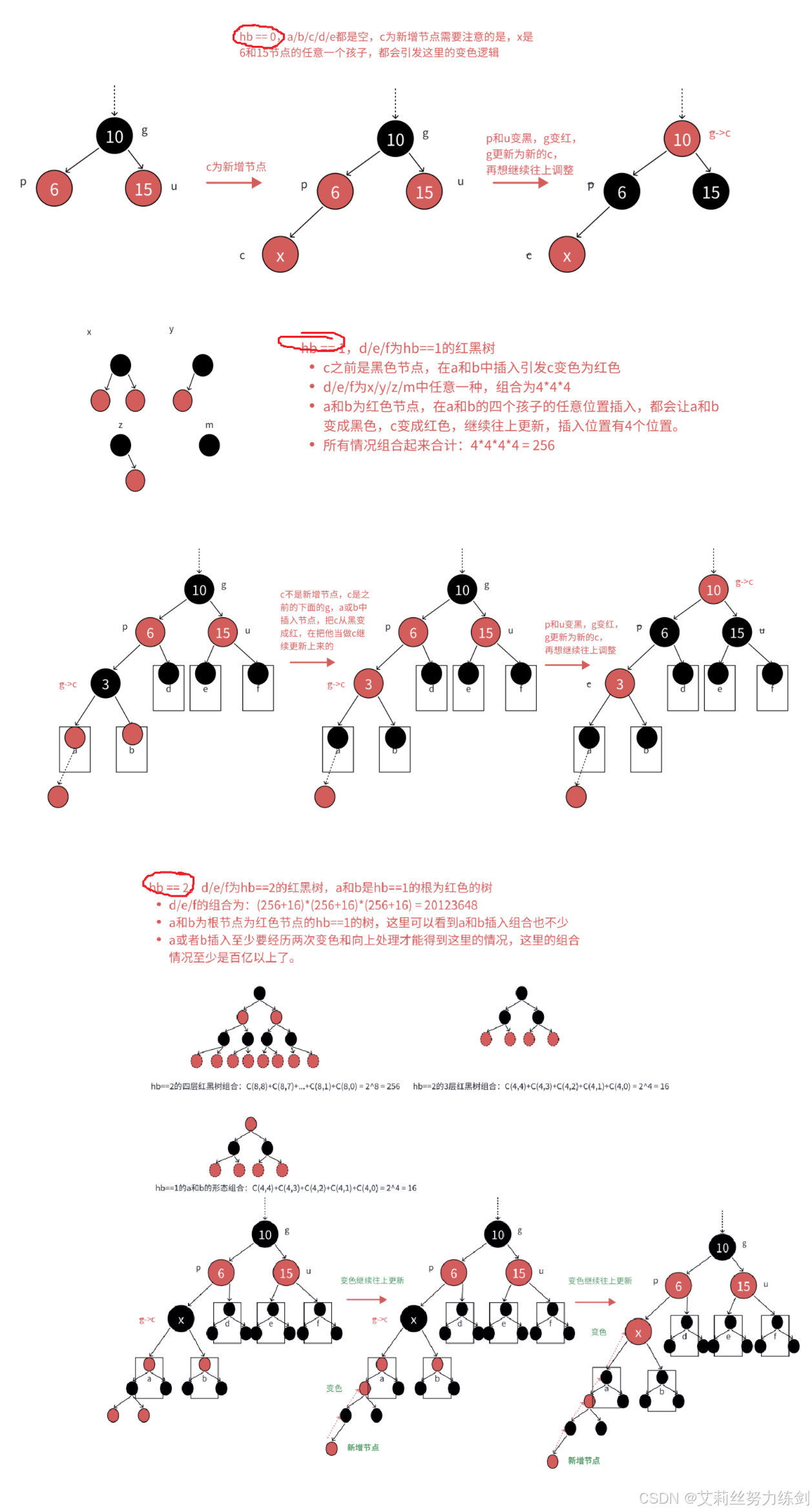
当hb等于2时,这里组合情况上百亿种,这些样例是帮助我们理解,不论情况多少种,有多么复杂,处理方式都是一样的,变色再继续往上处理即可,所以我们只需要看抽象图即可。
3.2.4 情况2:单旋 + 变色
c为红,p为红,g为黑,u不存在或者u存在且为黑,u不存在,则c一定是新增结点,u存在且为黑,则c一定不是新增,c之前是黑色的,是在c的子树中插入,符合情况1,变色将c从黑色变成红色,更新上来的。
分析:p必须变黑,才能解决,连续红色结点的问题,u不存在或者是黑色的,这里单纯的变色无法解决问题,需要旋转+变色。
如果p是g的左,c是p的左,那么以g为旋转点进行右单旋,再把p变黑,g变红即可。p变成课这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点了,且不需要往上更新,因为p的父亲是黑色还是红色或者空都不违反规则。

如果p是g的右,c是p的右,那么以g为旋转点进行左单旋,再把p变黑,g变红即可。p变成课这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点了,且不需要往上更新,因为p的父亲是黑色还是红色或者空都不违反规则。
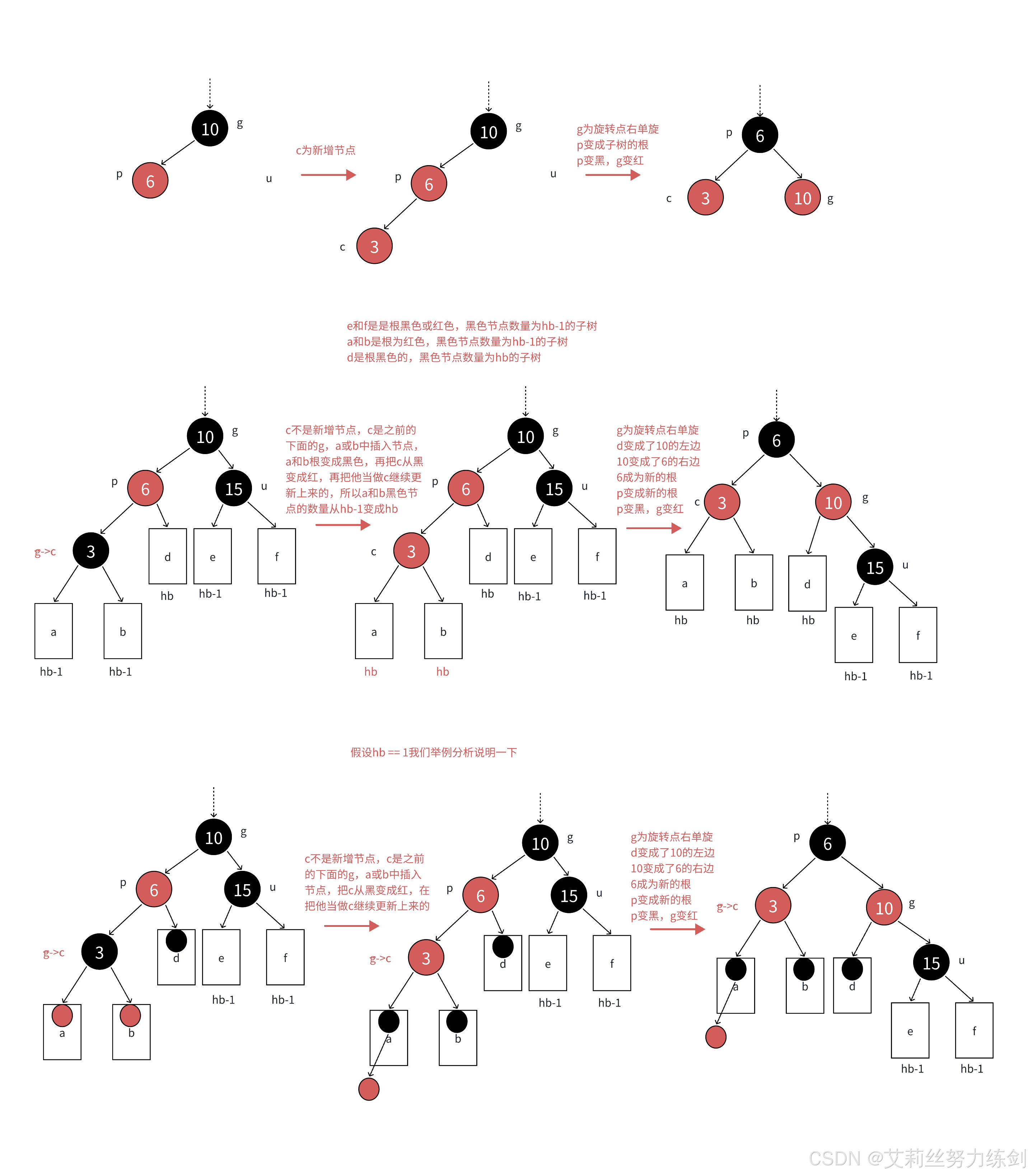
3.2.5 情况3:双旋 + 变色
c为红,p为红,g为黑,u不存在或者u存在且为黑,u不存在,则c一定是新增结点,u存在且为黑,则c一定不是新增,c之前是黑色的,是在c的子树中插入,符合情况1,变色将c从黑色变成红色,更新上来的。
分析:p必须变黑,才能解决,连续红色结点的问题,u不存在或者是黑色的,这里单纯的变色无法解决问题,需要旋转+变色。

如果p是g的左,c是p的右,那么先以p为旋转点进行左单旋,再以g为旋转点进行右单旋,再把c变
黑,g变红即可。c变成课这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点了,且不需要往上更新,因为c的父亲是黑色还是红色或者空都不违反规则。

如果p是g的右,c是p的左,那么先以p为旋转点进行右单旋,再以g为旋转点进行左单旋,再把c变
黑,g变红即可。c变成课这颗树新的根,这样子树黑色结点的数量不变,没有连续的红色结点了,且不需要往上更新,因为c的父亲是黑色还是红色或者空都不违反规则。
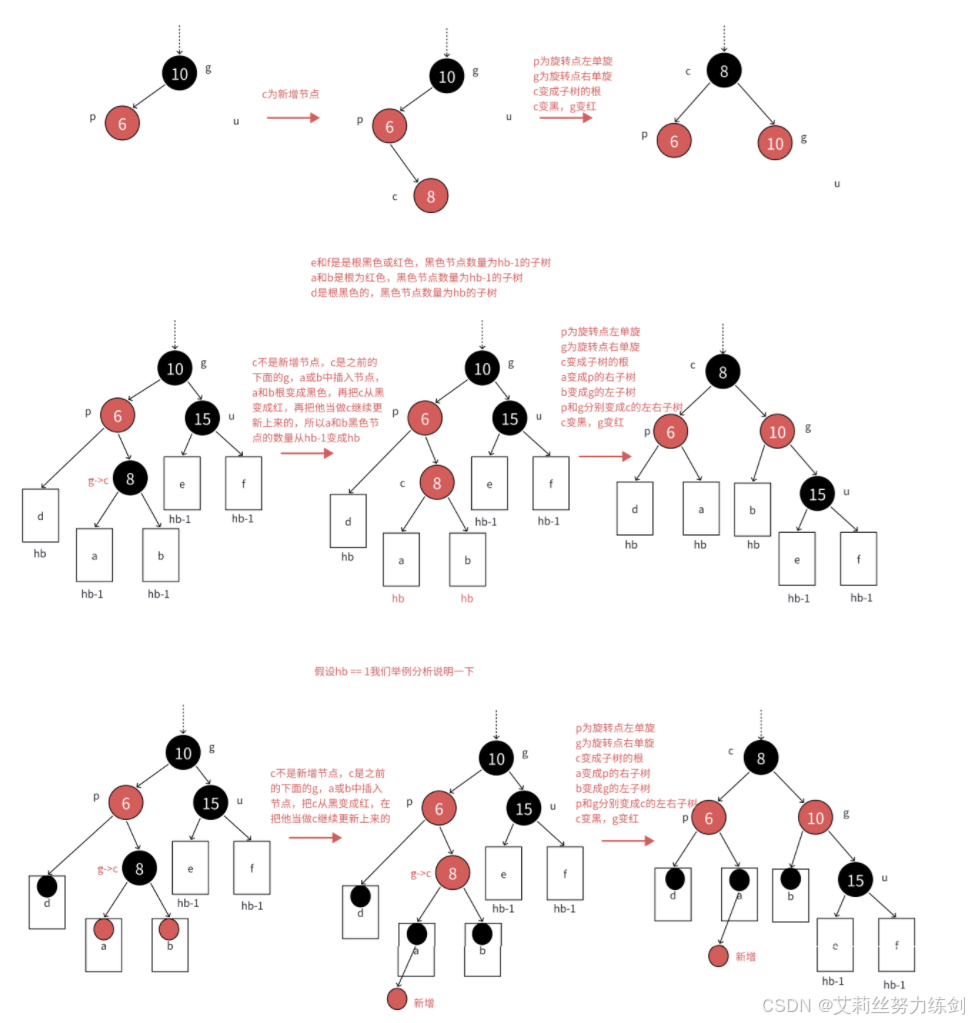
3.2.6 红黑树插入的代码实现
代码如下所示------
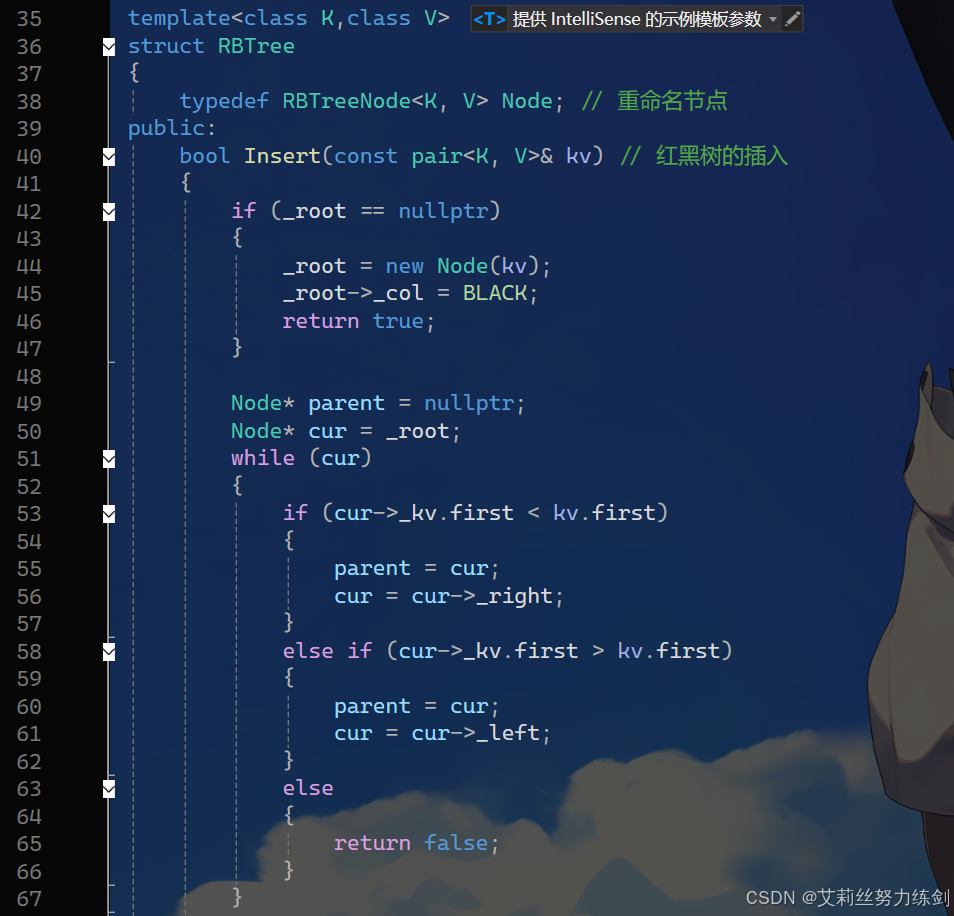
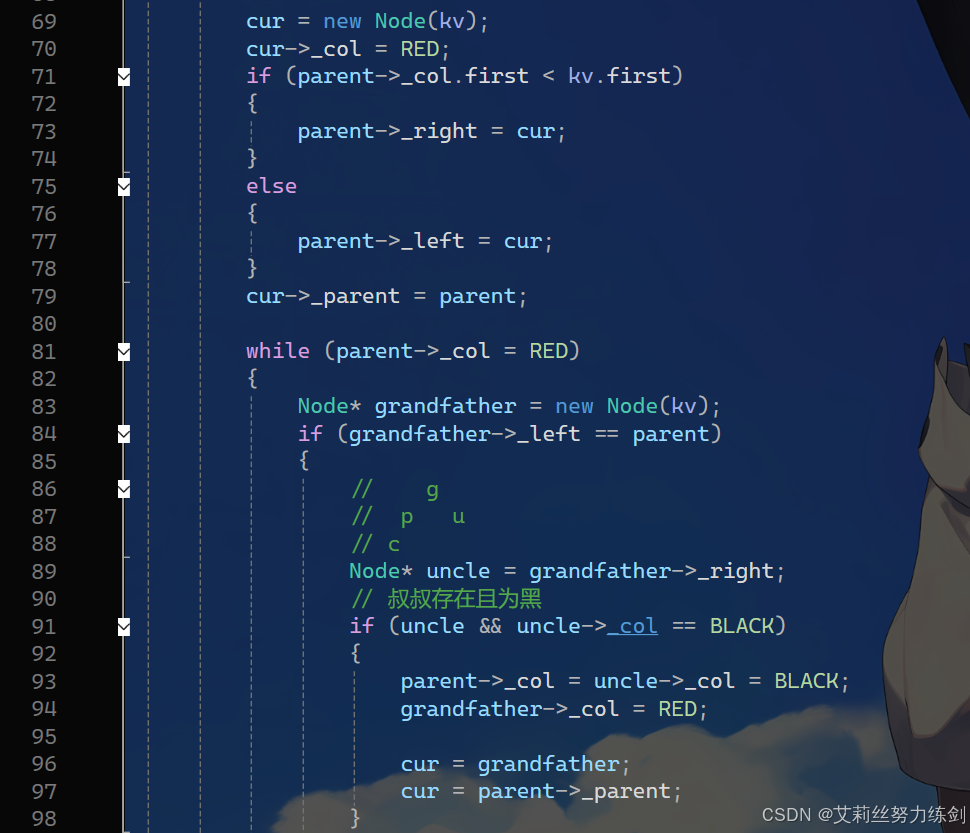
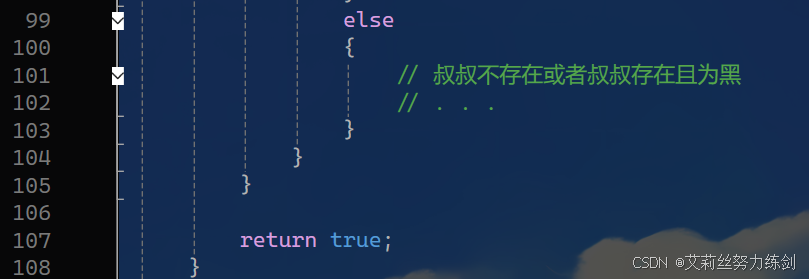
3.3 红黑树的旋转
3.3.1 右旋
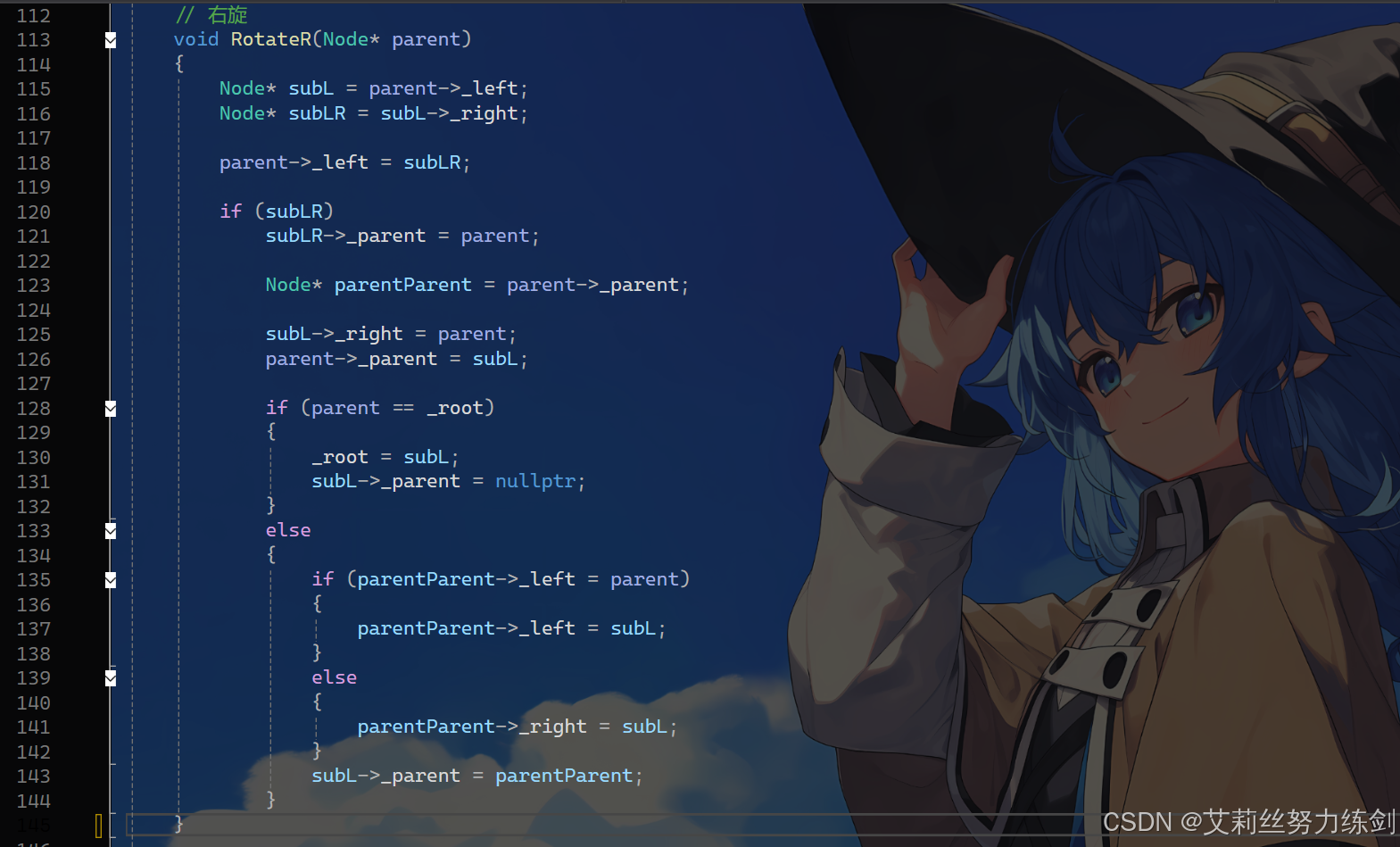
3.3.2 左旋

3.3.3 左右双旋
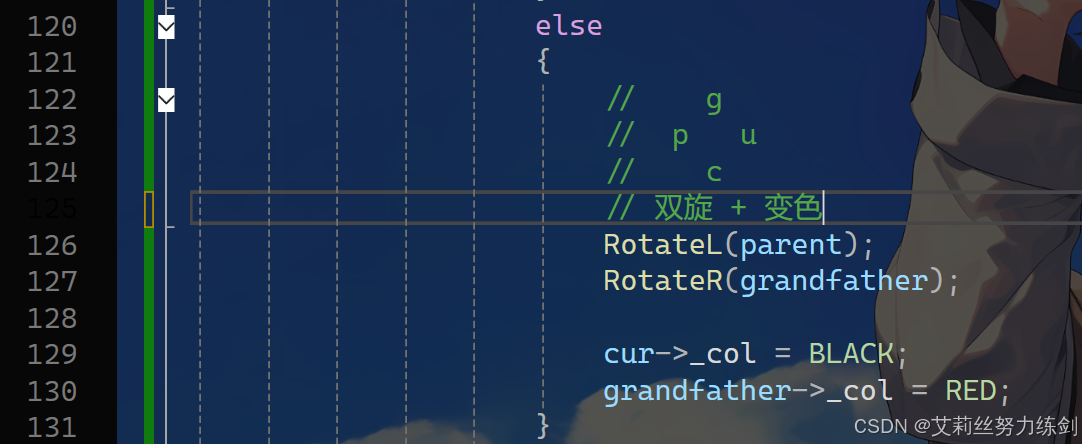
3.3.4 右左双旋

3.4 红黑树的查找问题
红黑树的查找就按搜索二叉树的逻辑来实现就可以了,时间复杂度是O(logn)。
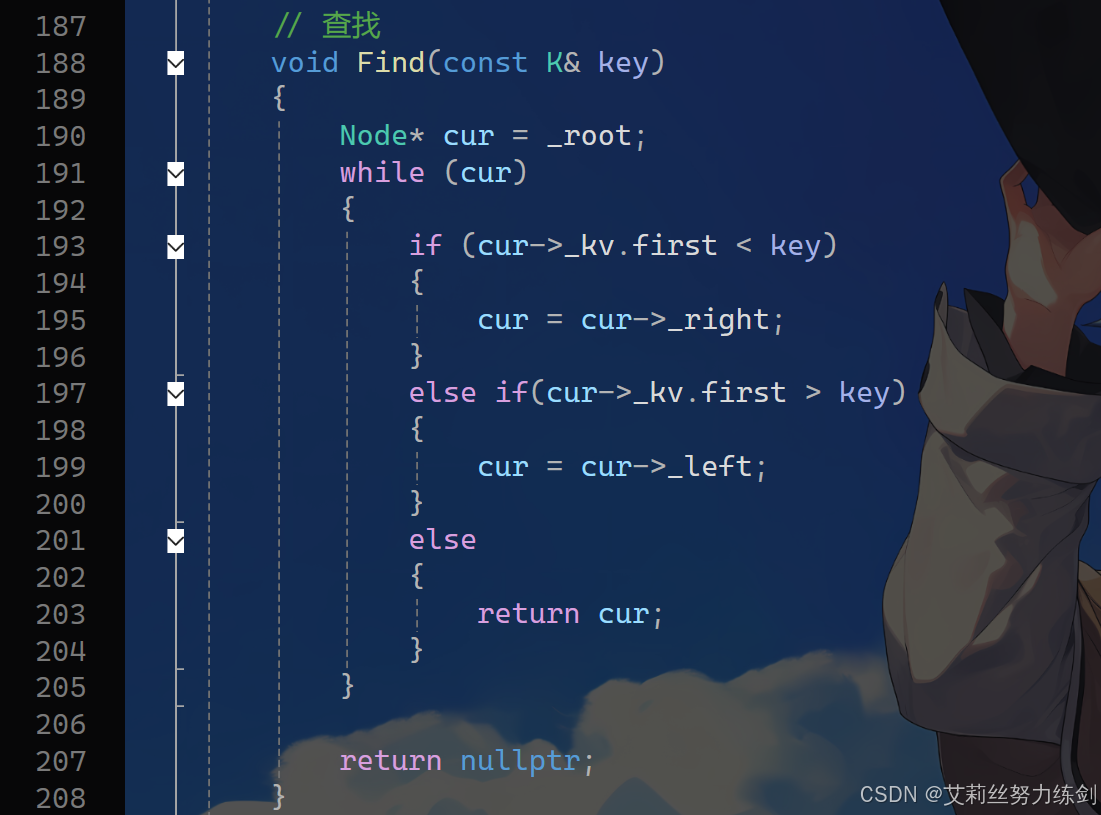
3.5 Size()
还是同样的问题,这里传根不能直接传,得从外部调用内部的函数完成传根------
核心原因:封装性 vs 递归需求的矛盾
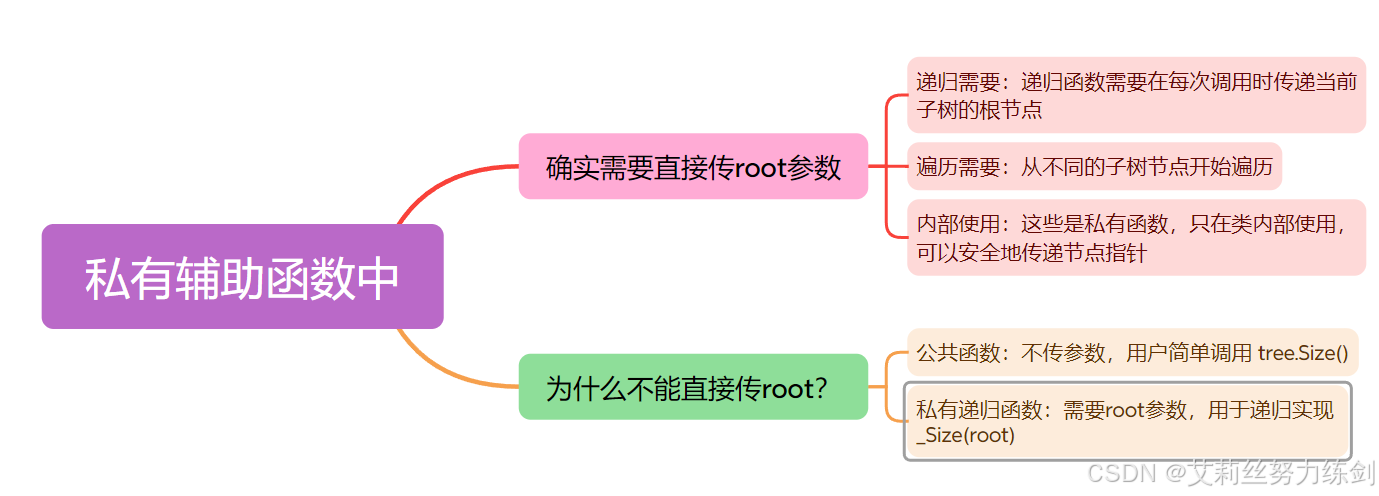
3.5.1 公共接口:不需要传root
cpp
public:
int Size() { return _Size(_root); } // 用户只需调用 tree.Size()
int Height() { return _Height(_root); } // 简单、安全、易用3.5.2 私有实现:必须传root
cpp
private:
int _Size(Node* root) { // 递归必须传当前节点
if (root == nullptr) return 0;
return _Size(root->_left) + _Size(root->_right) + 1; // 递归调用
}3.5.3 解决方案:双重接口设计
因此我们的解决方案如下------
3.5.3.1 公共层(面向用户)
cpp
// 用户看到的简单接口
tree.Size(); // 不需要参数
tree.Height(); // 直接使用
tree.IsBalanceTree();3.5.3.2 私有层(内部递归)
cpp
// 递归实现的辅助函数
_Size(root); // 需要节点参数
_Height(root); // 支持递归遍历
_IsBalanceTree(root);3.5.4 为什么要设计成双重接口?
cpp
// 方案1:让用户传root(不好)
tree.Size(someNode); // 用户可能传错节点,不安全
// 方案2:放弃递归(不好)
// 用迭代实现Size(),但代码复杂,性能可能更差
// 方案3:暴露_root(很不好)
tree._Size(tree._root); // 破坏封装,会很危险,不安全3.5.5 总结
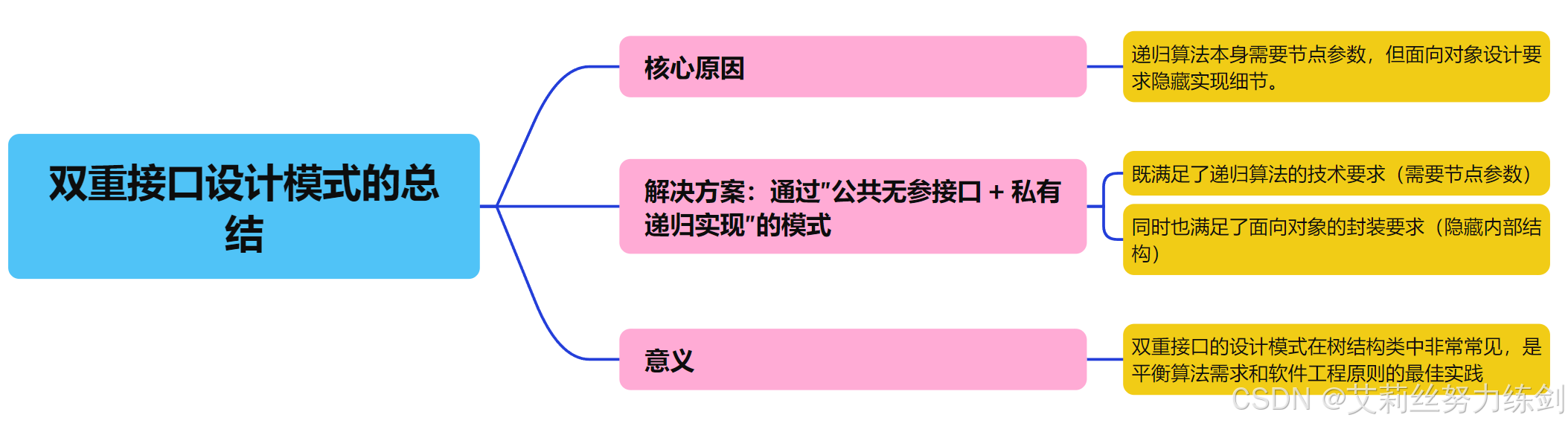
3.5.6 Size()双重接口设计实现
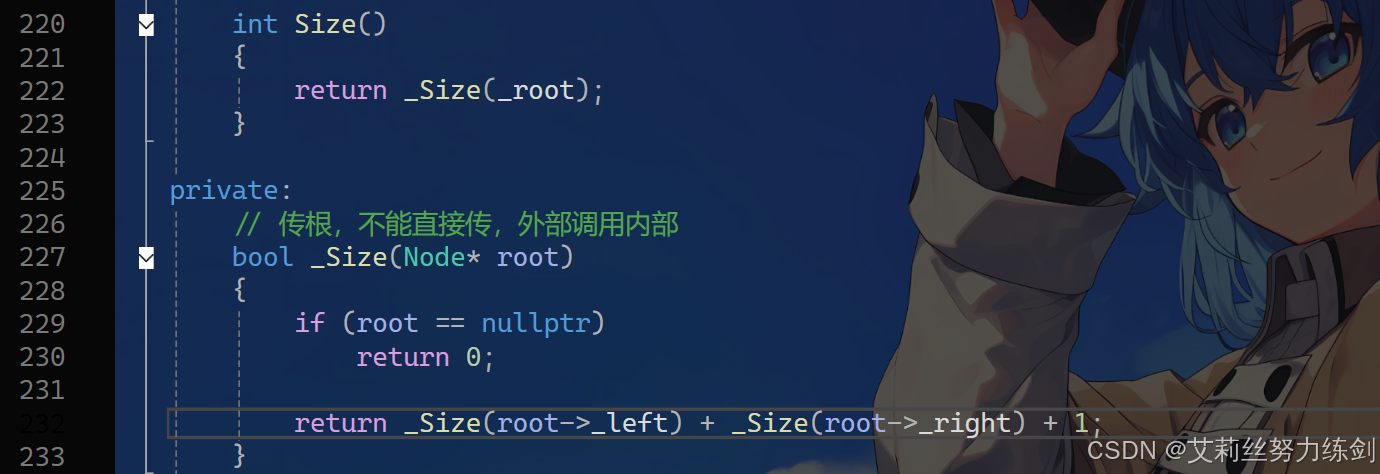
3.6 Height()
外部(public)------
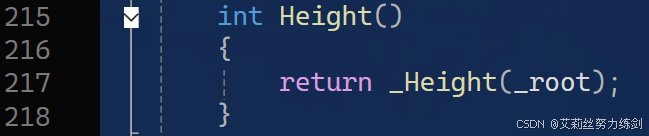
内部(private)------
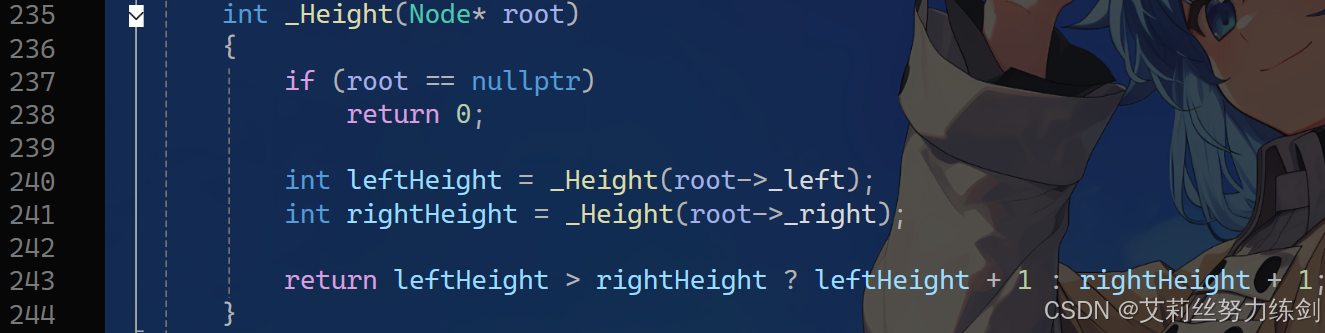
3.7 IsBalanceTree()
外部(public)------
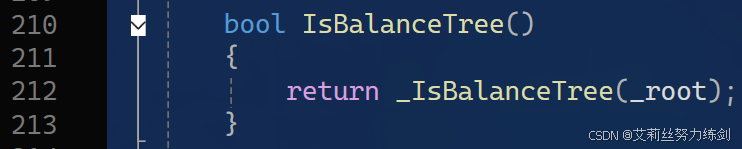
内部(private)------

3.8 中序遍历:InOrder()
外部(public)------

内部(private)------
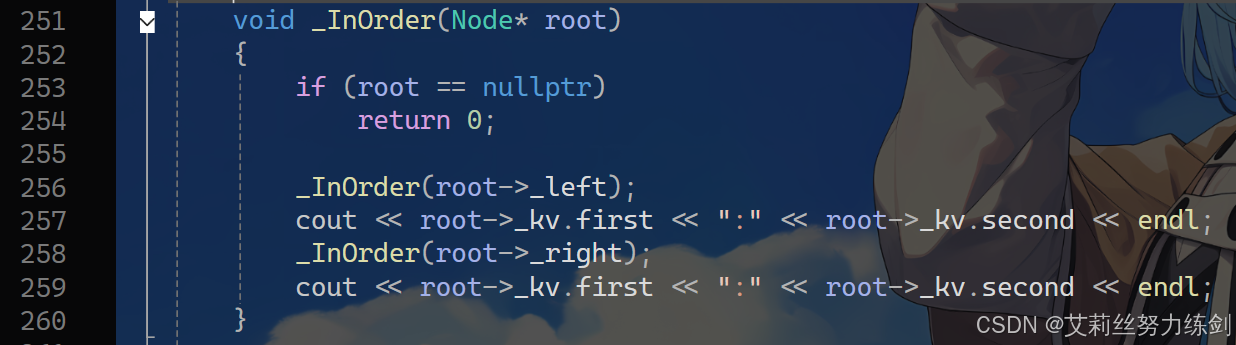
3.9 验证红黑树
这里获取最长路径和最短路径,检查最长路径不超过最短路径的2倍是不可行的,因为就算满足这个条件,红黑树也可能颜色不满足规则,当前暂时没出问题,后续继续插入还是会出问题的。所以我们还是去检查4点规则,满足这4点规则,一定能保证最长路径不超过最短路径的2倍。
1、规则1枚举颜色类型,天然实现保证了颜色不是黑色就是红色。
2、规则2直接检查根即可。
3、规则3前序遍历检查,遇到红色结点查孩子不太方便,因为孩子有两个,且不一定存在,反过来检查父亲的颜色就方便多了,即孩子不一定存在,父亲一定存在。
4、规则4前序遍历,遍历过程中用形参记录根节点到当前结点的blackNum(黑色结点数量),前序遍历遇到黑色结点就++blackNum,走到空就计算出了一条路径的黑色结点数量。再任意一条路径黑色结点数量作为参考值,依次比较即可。
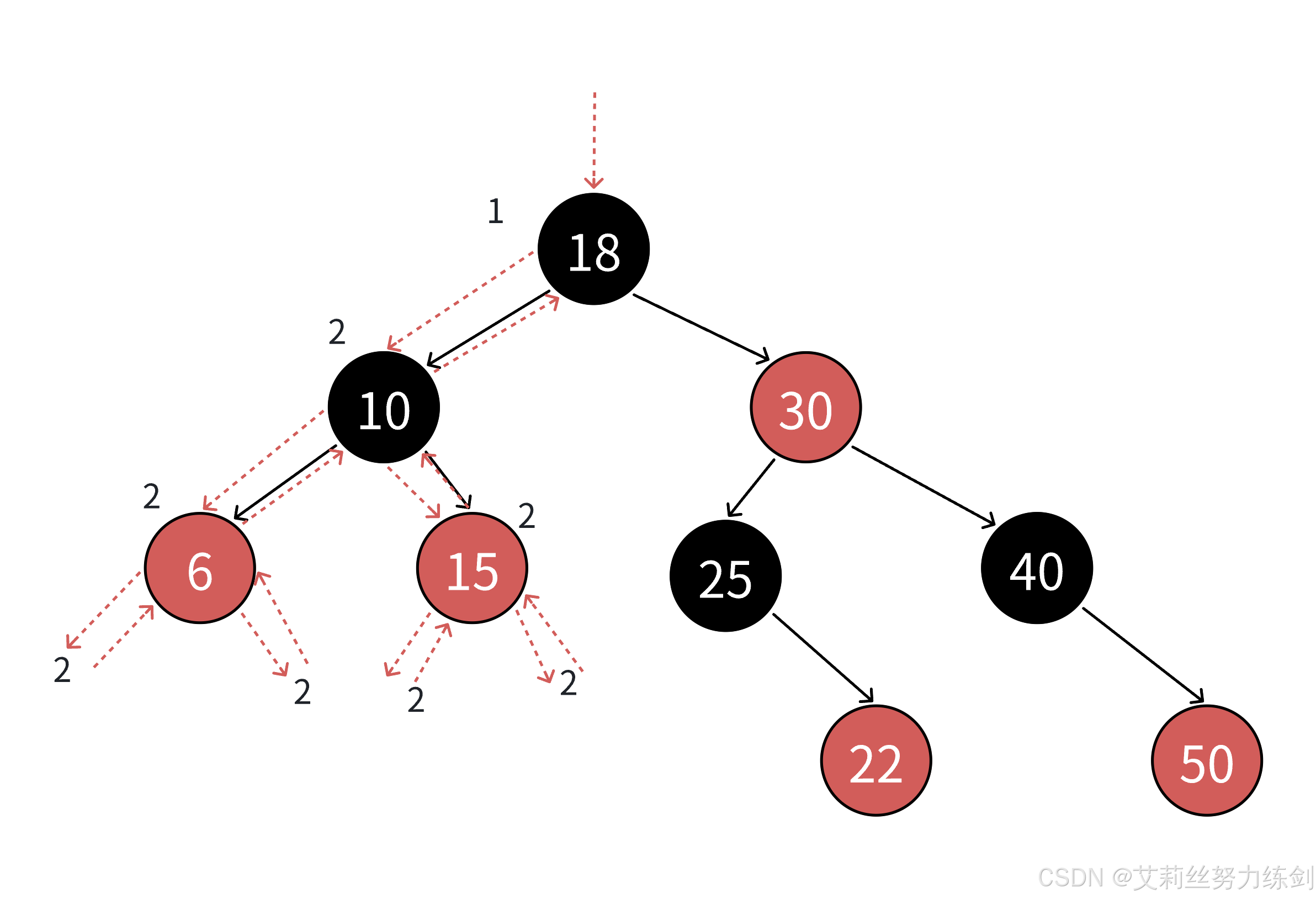


3.10 红黑树的删除
和AVL树那里一样,红黑树这里的删除我们也不做讲解------

有兴趣的uu们可以去看一下参考资料,书的话推荐uu们去看一下《算法导论》或者《STL源码剖析》,这两本书里面会有讲解。
完整代码示例与实践演示
RBTree.h:
cpp
#pragma once
#include<iostream>
using namespace std;
#include<assert.h>
// 枚举值表示颜色
// 保障不是黑色就是红色
enum Color
{
BLACK,
RED
};
// 这里我们默认按key / value结构实现
// 构造
template<class K,class V>
struct RBTreeNode
{
// 更新控制平衡也要加入parent指针
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Color _col;
// 初始化
RBTreeNode(const pair<K, V>& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(RED)
{}
};
template<class K,class V>
struct RBTree
{
typedef RBTreeNode<K, V> Node; // 重命名节点
public:
bool Insert(const pair<K, V>& kv) // 红黑树的插入
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
// 插入的是红色的节点(新增)
cur = new Node(kv);
cur->_col = RED;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
cur->_parent = parent;
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
// g
// p u
// c
Node* uncle = grandfather->_right;
// 叔叔存在且为黑
if (uncle && uncle->_col == RED)
{
// 变色 + 继续往上处理
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else
{
// 叔叔不存在或者叔叔存在且为黑
// g
// p u
// c
// 单旋 + 变色
if (cur == parent->_left)
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// p u
// c
// 双旋 + 变色
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
// g
// u p
Node* uncle = grandfather->_left;
// 叔叔存在且为红->变色即可
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
// 继续往上处理
cur = grandfather;
parent = cur->_parent;
}
else
{
// 情况二:叔叔不存在或者存在且为黑
// 旋转 + 变色
// g
// u p
// c
if (cur == parent->_right)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
// g
// u p
// c
RotateR(parent);
RotateL(grandfather);
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK; // 不去判断,直接变成黑的
return true;
}
// -------------旋转----------------
// 右旋
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* parentParent = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
if (parent == _root)
{
_root = subL;
subL->_parent = nullptr;
}
else
{
if (parentParent->_left == parent)
{
parentParent->_left = subL;
}
else
{
parentParent->_right = subL;
}
subL->_parent = parentParent;
}
}
// 左旋
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
// 处理 subRL 与 parent 的关系
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* parentParent = parent->_parent;
// 处理 subR 与 parent 的关系
subR->_left = parent;
parent->_parent = subR;
// 处理 subR 与 parentParent 的关系
if (parentParent == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
subR->_parent = parentParent;
}
}
// 中序遍历
void InOrder()
{
_InOrder(_root);
cout << endl;
}
// 查找
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key)
{
cur = cur->_right;
}
else if(cur->_kv.first > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool IsBalanceTree()
{
if (_root && _root->_col == RED)
return false;
// 最左路径黑色节点的数量做参考值,去比较其他路径
int left_bn = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
left_bn++;
cur = cur->_left; // 不加上会死循环
}
return _Checkcolor(_root, 0, left_bn);
}
int Height()
{
return _Height(_root);
}
int Size()
{
return _Size(_root);
}
private:
// 传根,不能直接传,外部调用内部
int _Size(Node* root)
{
if (root == nullptr)
return 0;
return _Size(root->_left) + _Size(root->_right) + 1;
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
// root_cur_bn 根节点到当前节点路径上的黑色节点的数量
// 前序递归
bool _Checkcolor(Node* root, int root_cur_bn,const int left_bn)
{
if (root == nullptr)
{
// 检查每条路径的黑色节点数量
if (root_cur_bn != left_bn)
{
cout << "黑色节点的数量不相等" << endl;
return false;
}
return true;
}
if (root->_col == BLACK)
{
root_cur_bn++;
}
// 检查连续的红色节点
if (root->_col == RED && root->_parent && root->_parent->_col == RED)
{
cout << root->_kv.first << "存在连续的红色节点" << endl;
return false;
}
return _Checkcolor(root->_left, root_cur_bn, left_bn)
&& _Checkcolor(root->_right, root_cur_bn, left_bn);
}
int _InOrder(Node* root)
{
if (root == nullptr)
return 0;
_InOrder(root->_left);
//cout << root->_kv.first << ":" << root->_kv.second << endl;
cout << root->_kv.first << " ";
_InOrder(root->_right);
////cout << root->_kv.first << ":" << root->_kv.second << endl;
}
private:
Node* _root = nullptr;
};Tree.cpp:
cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<vector>
using namespace std;
#include"RBTree.h"
void TestRBTree1()
{
RBTree<int, int>t;
// 常规的测试用例
int a[] = { 4,2,6,1,3,5,15,7,16,14 };
for (auto e : a)
{
if (e == 7)
{
int i = 0;
}
t.Insert({ e,e });
cout << "Insert:" << e << "->";
t.InOrder();
}
t.InOrder();
//cout << t.IsBalanceTree() << endl;
}
// 插入一堆随机值,测试平衡,顺便测试一下高度和性能
void TestRBTree2()
{
const int N = 1000000;
vector<int> v;
v.reserve(N);
srand(time(0));
for (size_t i = 0; i < N; i++)
{
v.push_back(rand() + i);
}
size_t begin2 = clock();
RBTree<int, int> t;
for (auto e : v)
{
t.Insert(make_pair(e, e));
}
size_t end2 = clock();
cout << "Insert:" << end2 - begin2 << endl;
cout << t.IsBalanceTree() << endl;
cout << "Height:" << t.Height() << endl;
cout << "Size:" << t.Size() << endl;
size_t begin1 = clock();
// 确定在的值
/*for (auto e : v)
{
t.Find(e);
}*/
// 随机值
for (size_t i = 0; i < N; i++)
{
t.Find((rand() + i));
}
size_t end1 = clock();
cout << "Find:" << end1 - begin1 << endl;
}
int main()
{
//TestRBTree1();
TestRBTree2();
return 0;
}运行结果
TestRBTree1()
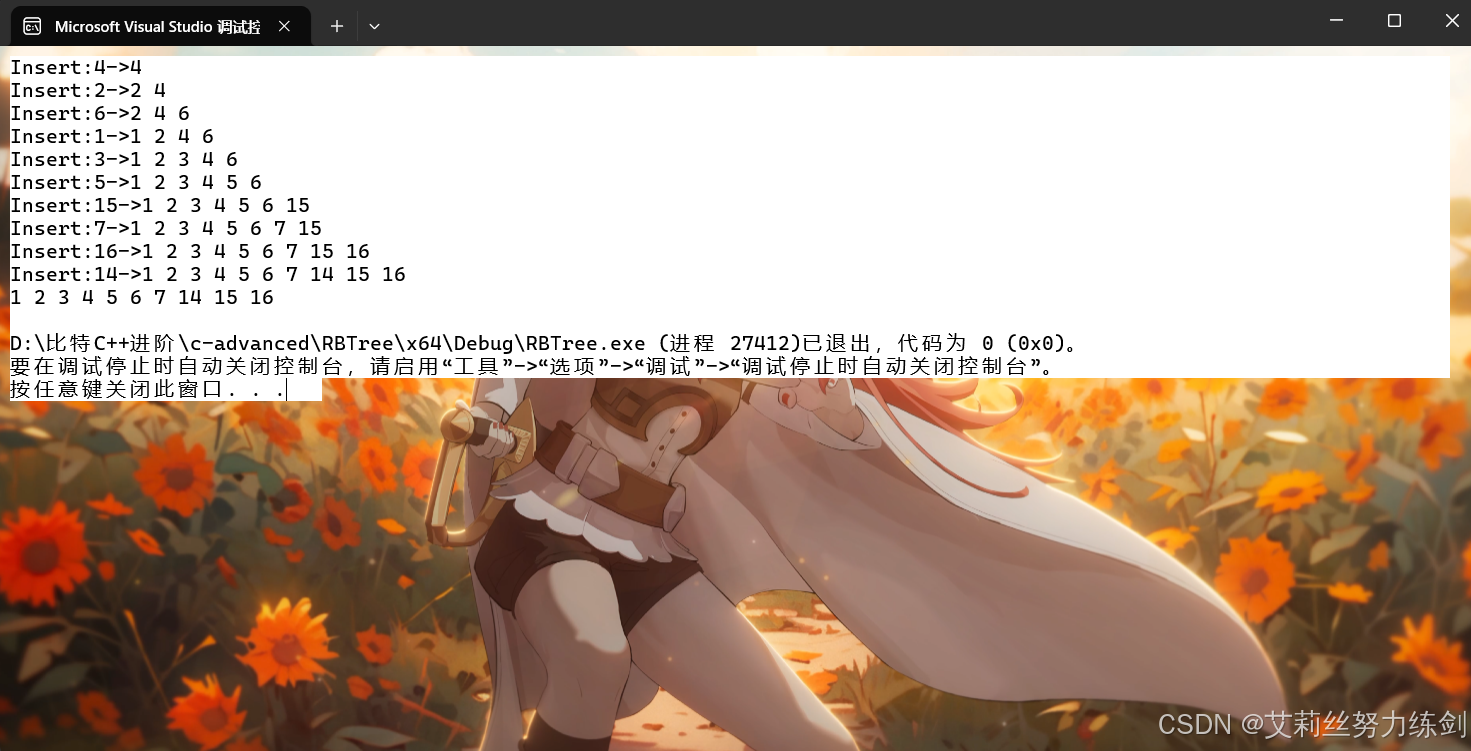
TestRBTree2()
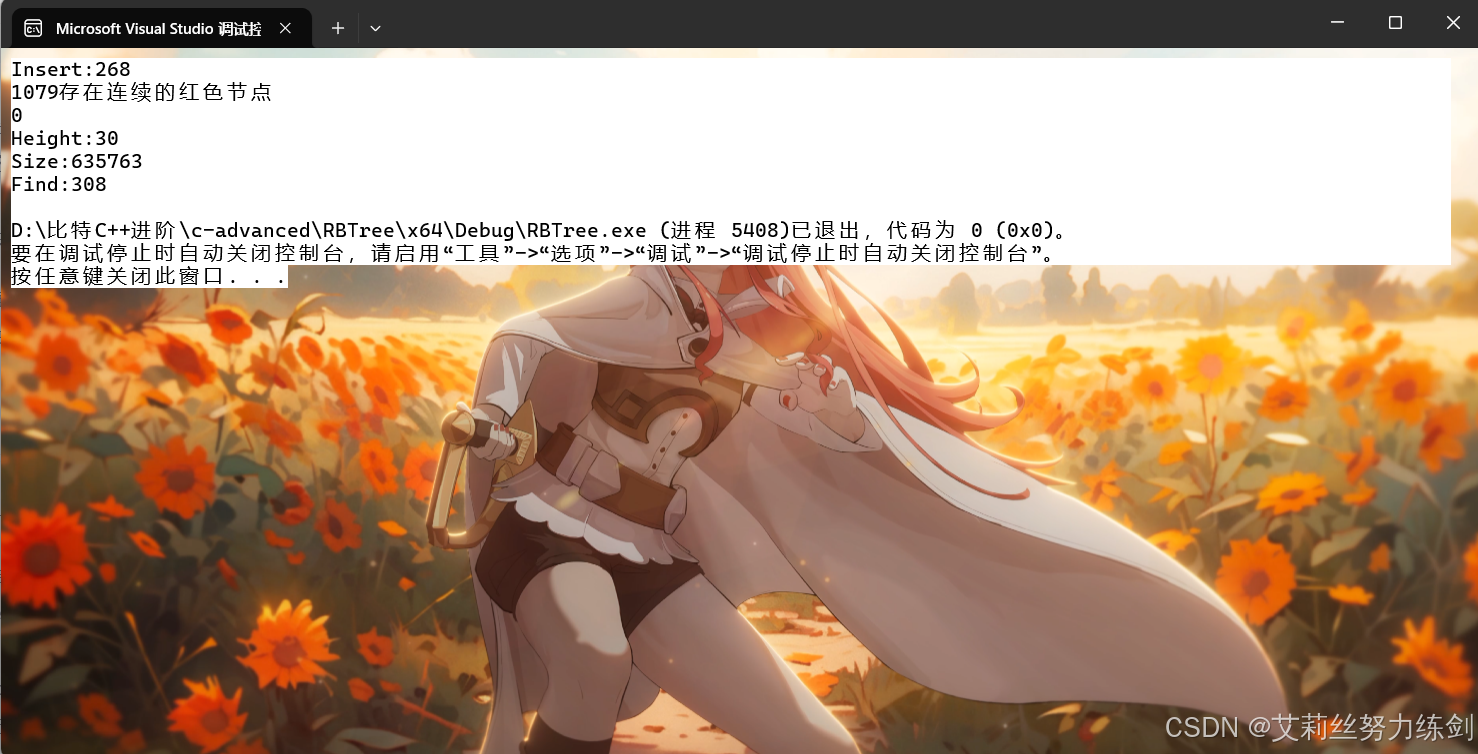
结尾
往期回顾:
【C++:AVL树】深入理解AVL树的平衡之道:从原理、旋转到完整实现代码
结语:都看到这里啦!那请大佬不要忘记给博主来个"一键四连"哦!
🗡博主在这里放了一只小狗,大家看完了摸摸小狗放松一下吧!🗡
૮₍ ˶ ˊ ᴥ ˋ˶₎ა
