一维前缀和与二维前缀和算法介绍及使用

[1. 一维前缀和](#1. 一维前缀和)

[1.1 一维前缀和原理讲解](#1.1 一维前缀和原理讲解)

[1.2 具体代码实现以及例题讲解](#1.2 具体代码实现以及例题讲解)

[2. 二维前缀和](#2. 二维前缀和)

[2.1 二维前缀和原理讲解](#2.1 二维前缀和原理讲解)

[2.2 具体代码实现以及例题讲解](#2.2 具体代码实现以及例题讲解)

今天我们来聊聊一维前缀和算法，这个算法属于基础算法。

1. 一维前缀和

一维前缀和是一种高效处理数组区间求和问题的算法，通过预处理数组构建前缀和数组，能将区间和查询的时间复杂度从 O (n) 降至 O (1)。

简单来说它的本质就是预处理，在这一点上有点像字符串的KMP算法，都是通过预处理的方式来换取效率。

这种算法是专门用来处理多次求区间和问题的。

1.1 一维前缀和原理讲解

那么我们该怎么进行预处理呢，我们看下面这张图，下面那个表格就是我们的前缀和数组，一般来说我们使用vector来存储前缀和数组。

我们的前缀和数组的第0个位置一般来说都是直接置空的，这个的话是因为我们在代码实现的时候要通过前缀和数组前一个位置的值加原数据当前位置的值来确定前缀和当前位置的值，如果我们不给第一个位置放0的话，在代码实现的时候我们还需要进行特判，这个的话比较麻烦，而直接置空的话就没有这个问题了，所以我们一般是选择直接置空。

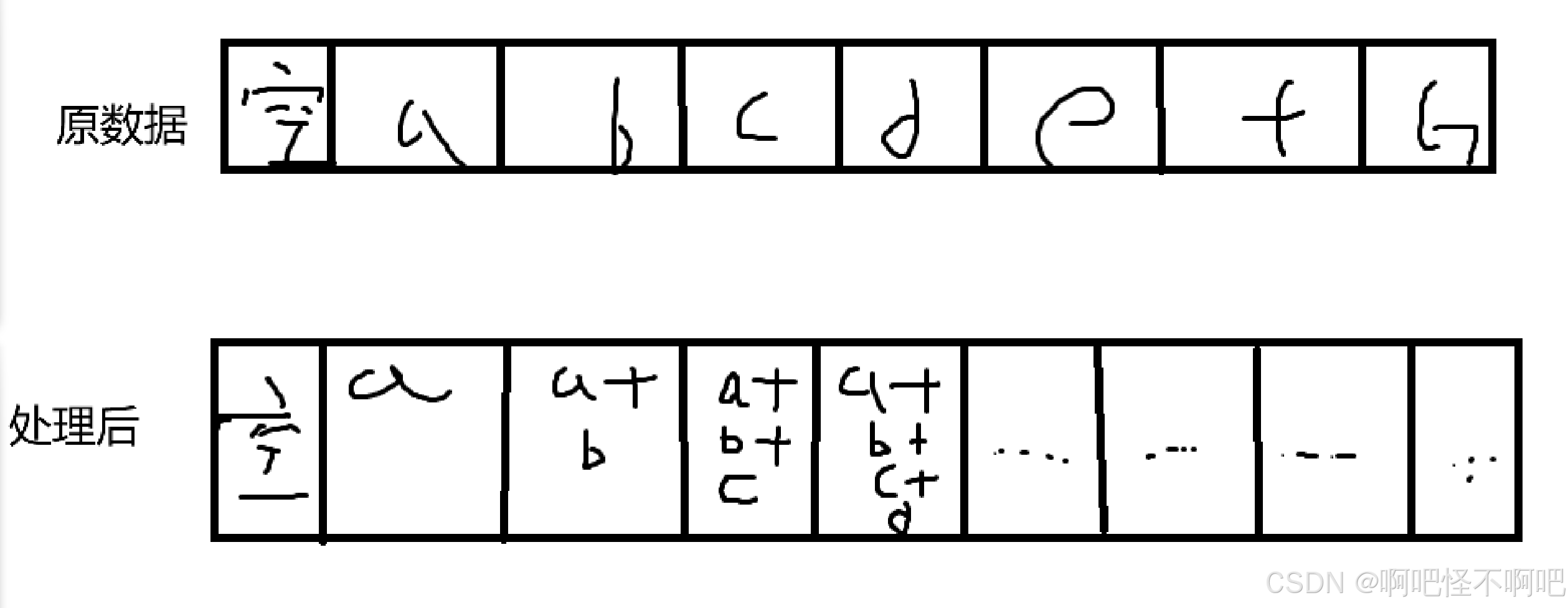
然后如果我们要求具体的某一段区间和的话，那么就要把结尾位置的值减去区间开头位置-1的值。

之所以要-1是因为区间开头的位置也是我们所需要的，所以-1后的位置才是具体要去掉的。

1.2 具体代码实现以及例题讲解

接下来我们通过一道例题，带大家理解前缀和的预处理方式。

我们看下面这张图片，题目给了一串数据然后要求我们的代码可以按要求连续求出要求查询的区间和。不要看现在好像就这么一点点数据，如果这个n无限变大的情况下，暴力的解法就肯定会超时的，

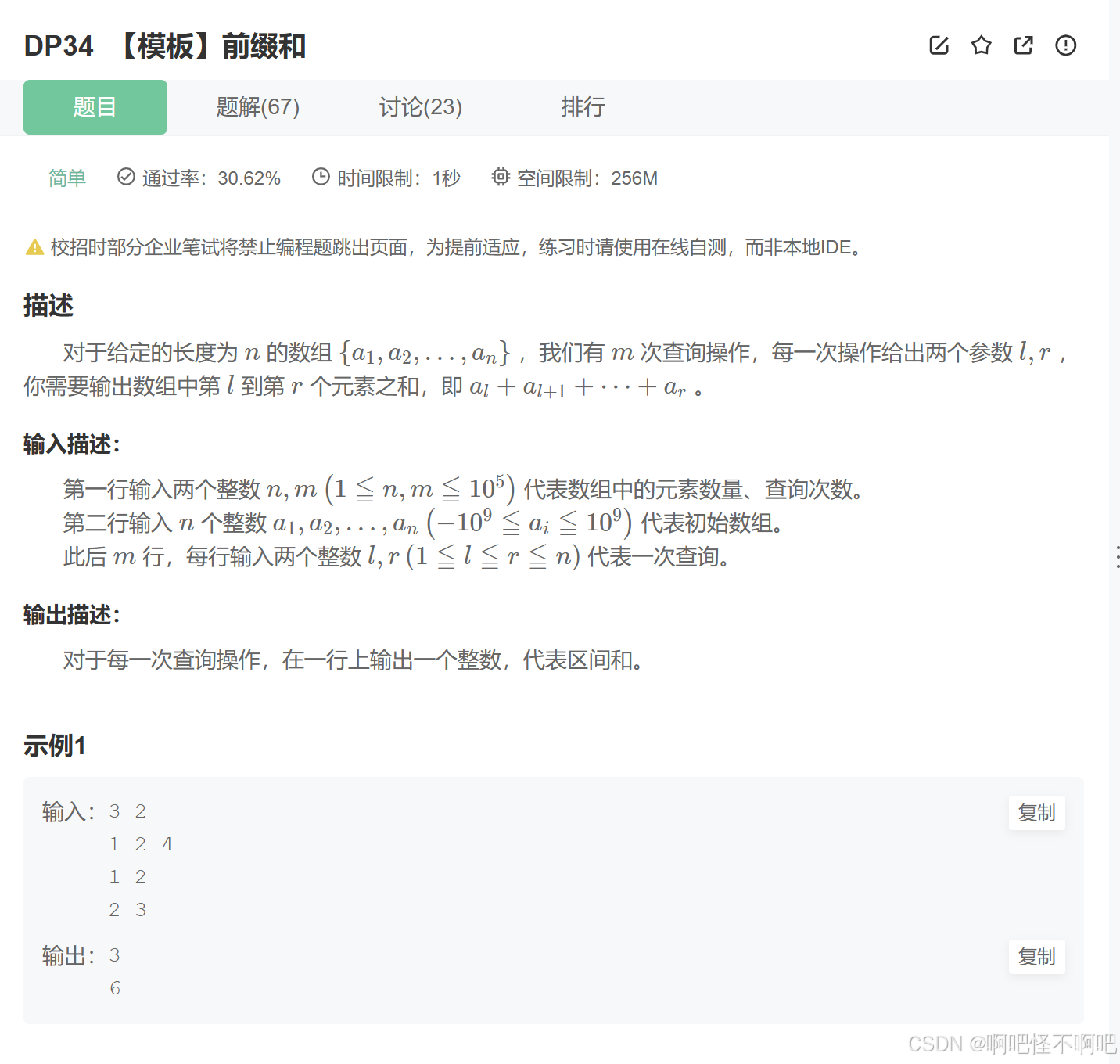
我们看下面这个代码，第二个for循环的作用就是构造一维前缀和数组，然后那个while循环里面的话就是计算出具体的区间和。

cpp 复制代码

#include<iostream>
#include<vector>
using namespace std;
int main()
{
    int n;
    int m;
    cin>>n>>m;
    vector<long long> nums(n+1);
    vector<long long> dp(n+1);
    for(int i=1;i<=n;++i)
        cin>>nums[i];
    for(int i=1;i<=n;++i)
        dp[i]=dp[i-1]+nums[i];
    while(m--)
    {
        int l,r;
        cin>>l>>r;
        long long sum=dp[r]-dp[l-1];
        cout<<sum<<endl;
    }
    return 0;
}

2. 二维前缀和

二维前缀和是一维前缀和在二维矩阵场景下的扩展，专门用于高效计算矩阵中任意子矩形区域的元素总和。它通过预处理构建前缀和矩阵，将单次子区域和的查询时间优化到 O (1)，非常适合需要频繁查询二维区域和的场景。

简单来说它就是在一维的基础上加了一维。同样，它也专门用来处理二维区间求和问题的。

2.1 二维前缀和原理讲解

二维前缀和的预处理和一维的有一点不一样的地方。那就是它在创建前缀和数组时需要减去重复加的地方，而在计算某一段区间和的时候想要加上被重复减去的部分。

我们看下面这个表格，如果我们的前缀和数组想要[i][j]位置的值，也就是拿到ABCD，那么就要一块一块的拿，我们先拿AB的位置，也就是[]i-1[j]，然后我们再拿AC的位置，也就是[i][j-1],然后在加上原数据中的[i][j]位置，最后我们发现A这个位置被重复加了两次，所以我们要减去A位置，也就是减去[i-1][j-1]。这样我们的二维前缀和数组就构建好了。

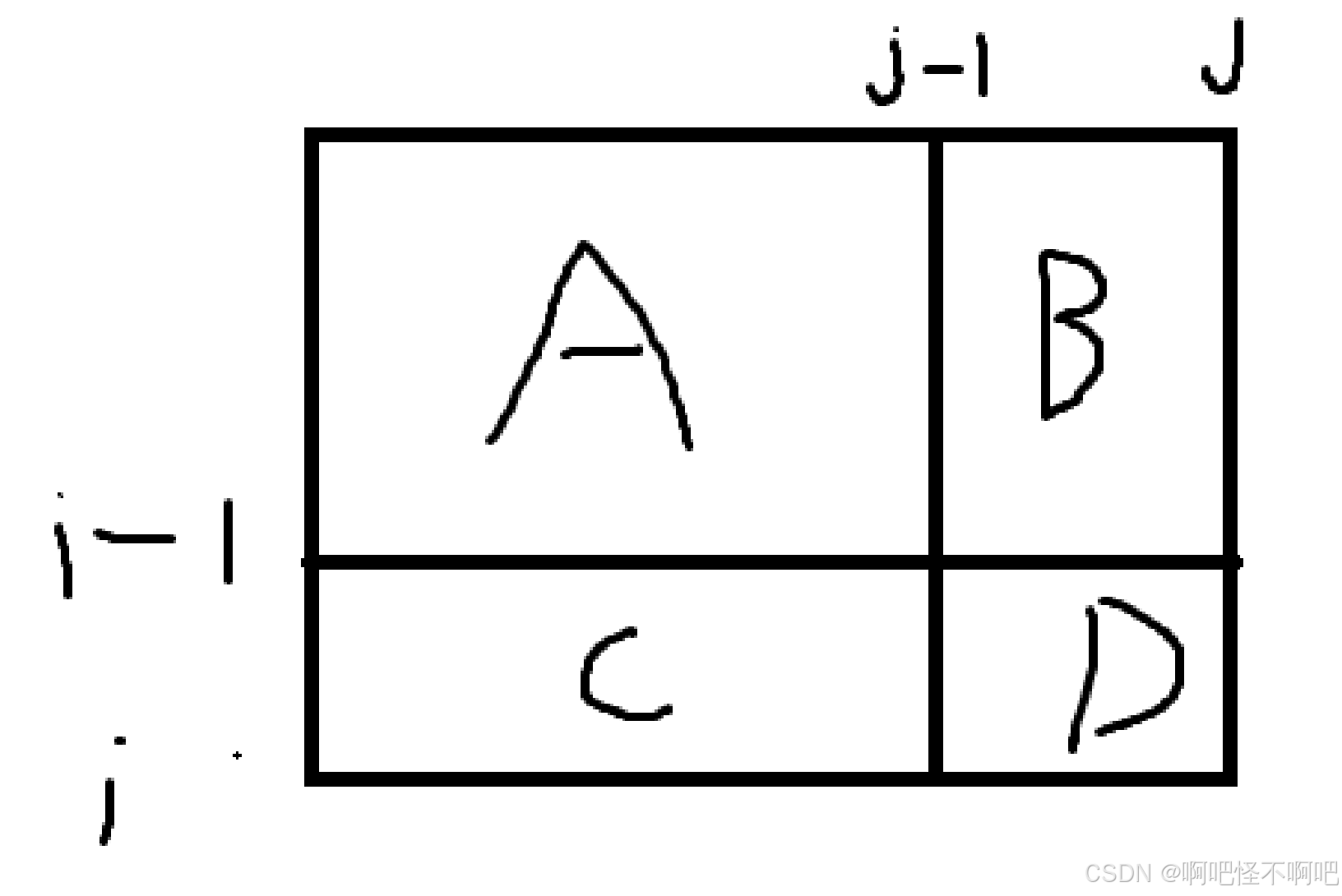
然后如果我们要算出具体的某一段的前缀。以D位置为例子，那么我们应该用总的减去部分，ABCD先减去AB再减去AC，最后我们在加上A那么我们就拿到了我们想要的D区域。

2.2 具体代码实现以及例题讲解

我们来看下面这道题，接下来我们通过这道题来详细的解释一下二维前缀和的原理。

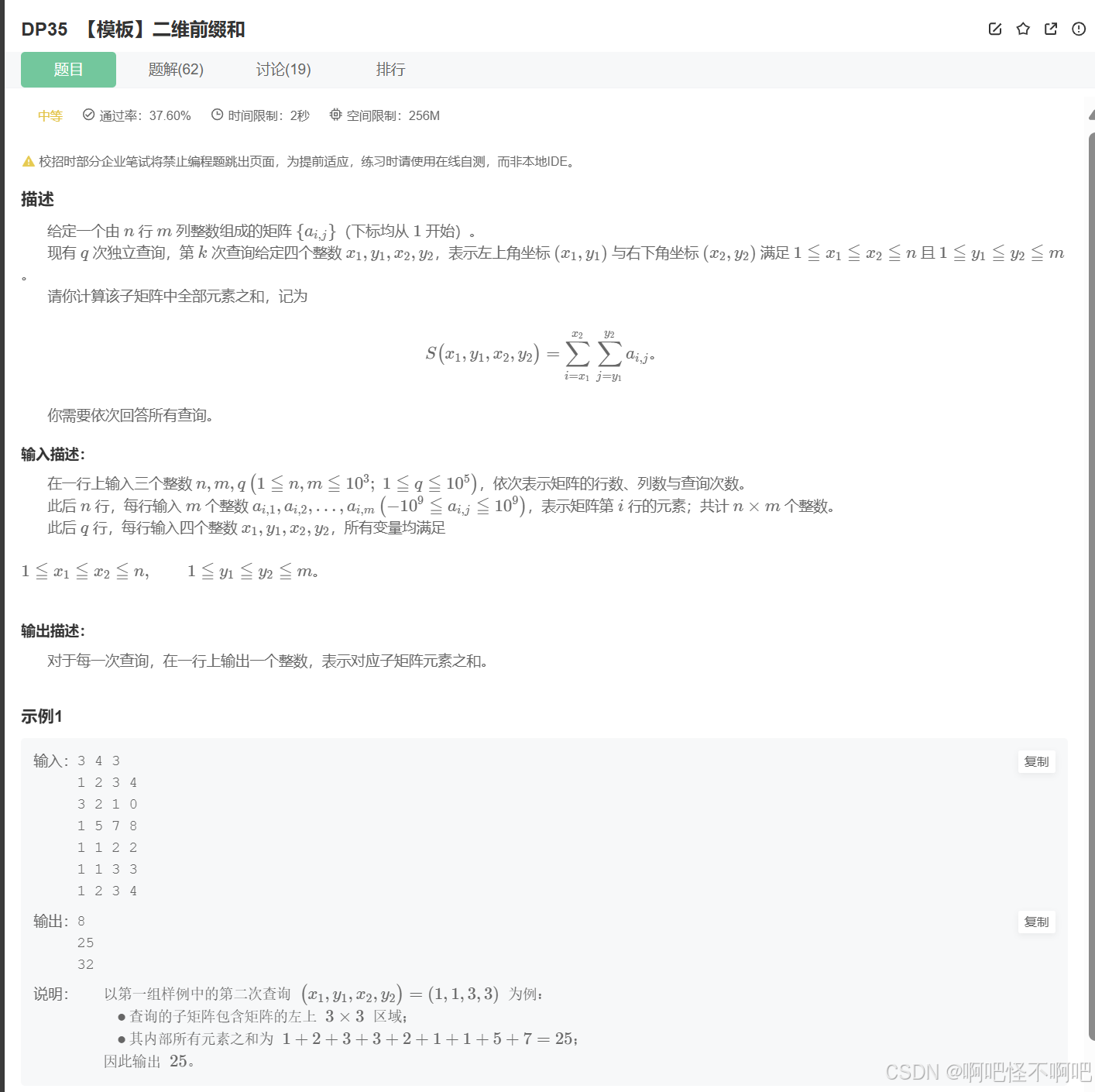
我们来看下面这个代码，第二个双层for循环来创建二维前缀和数组。接下来在while循环里面通过减去不要的部分来得到我们想要的区间和。

PS：之所以要a-1和b-1是因为a和b也是我们想要的部分，不可以被减去。所以最后加上的区域是[a-1][b-1]。

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

int main() {
    int n,m,q;
    cin>>n>>m>>q;
    vector<vector<ll>> nums(n+1, vector<ll>(m+1));
    vector<vector<ll>> dp(n+1, vector<ll>(m+1));
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)
            cin>>nums[i][j];
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)
            dp[i][j]=dp[i-1][j]+dp[i][j-1]+nums[i][j]-dp[i-1][j-1];
    while(q--)
    {
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        ll mysum=dp[c][d]-dp[a-1][d]-dp[c][b-1]+dp[a-1][b-1];
        cout<<mysum<<endl;
    }
   return 0;
}