
🫧个人主页: 小年糕是糕手
💫个人专栏:《数据结构(初阶)》** 《C/C++刷题集》 《C语言》**
🎨你不能左右天气,但你可以改变心情;你不能改变过去,但你可以决定未来!

目录
一、直接选择排序
选择排序的基本思想: 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
1.1、算法思想
- 在元素集合 array [i] - array [n - 1] 中选择关键码最大 (小) 的数据元素
- 若它不是这组元素中的最后一个 (第一个) 元素,则将它与这组元素中的最后一个(第一个)元素交换
- 在剩余的 array [i] - array [n - 2](array [i + 1] - array [n - 1])集合中,重复上述步骤,直到集合剩余 1 个元素
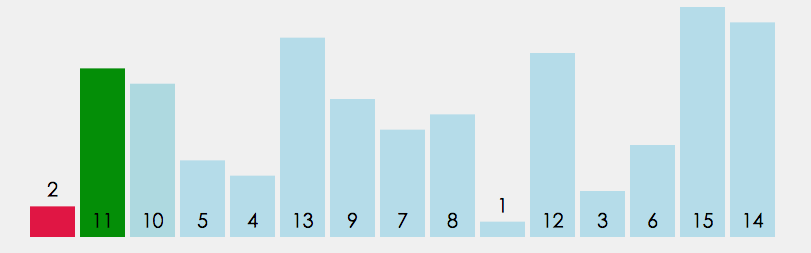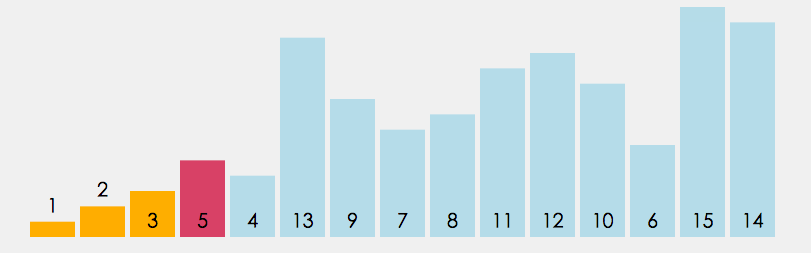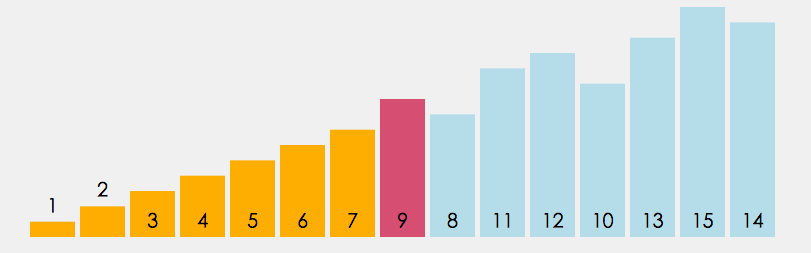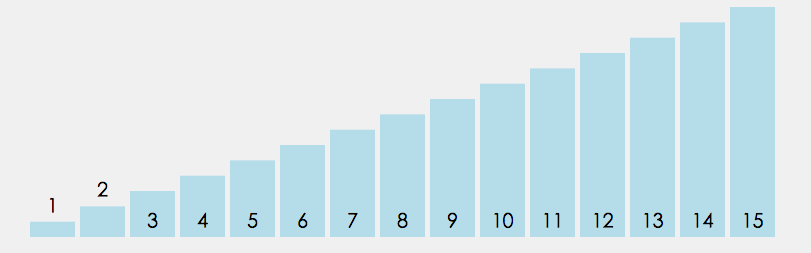
1.2、代码实现
cpp
void SelectSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int mini = begin;
int maxi = begin;
for (int i = begin + 1; i <= end; i++)
{
if (arr[i] < arr[mini])
{
mini = i;
}
if (arr[i] > arr[maxi])
{
maxi = i;
}
}
if (maxi == begin)
{
maxi = mini;
}
Swap(&arr[begin], &arr[mini]);
Swap(&arr[end], &arr[maxi]);
begin++;
end--;
}
}直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好,实际中很少使用(我们主要是通过这个例子去了解更多的排序算法,锻炼自己的代码能力)
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
二、堆排序
2.1、算法思想
堆排序的算法思想基于堆这种数据结构(完全二叉树),核心步骤如下:
构建初始堆:将待排序的数组视为一棵完全二叉树,调整其结构为大顶堆(或小顶堆,取决于排序需求)。大顶堆的特性是:每个父节点的值都大于或等于其左右子节点的值。
交换与调整堆:
- 将堆顶元素(最大值,对应大顶堆)与堆的最后一个元素交换,此时最大值被放置到数组末尾(即已排序位置)。
- 排除已排序的最后一个元素,将剩余元素重新调整为大顶堆(此时堆的规模减 1)。
重复操作:不断重复 "交换堆顶与当前堆的最后一个元素" 和 "调整剩余元素为大顶堆" 的步骤,直到堆的规模缩减为 1,此时整个数组完成排序。
通过堆的特性,每次能高效地选出剩余元素中的最大值(或最小值),最终实现整个数组的有序排列。堆排序的时间复杂度为O(n*logn),空间复杂度为O(1)。
大家要是想进一步详细了解可以参考:小年糕是糕手博客 -- 顺序结构二叉树详解
2.2、代码实现
cpp
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
//向上调整算法
void AdjustUp(int* arr, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
//建大堆: >
//建小堆: <
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
//不用调整符合情况
break;
}
}
}
//向下调整算法
//n是堆里面的结点个数,如果越界了就不需要调整了
void AdjustDown(int* arr, int parent, int n)
{
int child = parent * 2 + 1;
while (child < n)
{
//建大堆: <
//建小堆: >
if (child + 1 < n && arr[child] < arr[child + 1])
{
child++;
}
//孩子和父亲比较
//建大堆: >
//建小堆: <
if (arr[child] > arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int* arr, int n)
{
//向下调整算法 -- 建堆n
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, n);
}
////向上调整算法 -- 建堆n*logn
//for (int i = 0; i < n; i++)
//{
// AdjustUp(arr, i);
//}
//n*logn
int end = n - 1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
AdjustDown(arr, 0, end);
end--;
}
}堆排序的特性总结如下:
时间复杂度:O(n*logn)。构建初始堆的时间复杂度为O(n),后续每次调整堆的时间复杂度为O(logn),共需调整n−1次,整体复杂度稳定为O(n*logn),不受数据分布影响。
空间复杂度:O(1)。堆排序是原地排序算法,仅需常数级别的额外空间用于临时变量交换。
稳定性:不稳定。在交换堆顶元素与末尾元素时,可能会改变相同元素的相对顺序。
适用场景:适用于数据量较大的场景,对空间复杂度要求严格时表现较好,但由于交换和调整操作较频繁,实际应用中对小规模数据的效率可能不如快速排序。
其他特性:基于堆结构实现,排序过程中需要频繁进行堆的调整(下沉操作),逻辑相对直接选择排序更复杂,但效率更高。