【02】深入理解Harris角点检测：从原理推导到实战实现

简介

本文从特征与角点的基础概念入手，系统解析Harris角点检测的算法逻辑------通过窗口移动分析灰度变化、构建矩阵模型、计算响应值筛选角点，并结合Python-OpenCV完成实战实现。帮助读者理解如何将"人类视觉中的角点"转化为"计算机可识别的定量特征"，为图像拼接、目标跟踪等任务奠定基础。

一、背景：从"特征"到"角点"

1.1 什么是"特征"？

在数据挖掘中，特征是数据集的"本质标识" （比如用户的年龄、消费习惯）；在计算机视觉中，图像特征是能描述图像局部/整体内容的"关键信息"，主要分为两类：

• 区域特征：角点、边缘、斑点（与周围灰度/颜色差异明显的区域，比如地图中的一棵树、一栋房子）；
• 数据特征：对图像信息的抽象表示（比如将图像像素转化为向量）。

其中，角点是最常用的区域特征之一------它是图像轮廓的交点，即使视角变化也能保持稳定。

1.2 为什么需要"特征检测"？

人类能轻松识别图像中的"角点"（比如桌子的拐角、窗户的边角），但计算机只能处理"数值"。特征检测的核心是将视觉信息转化为定量数据，让计算机"读懂"图像。

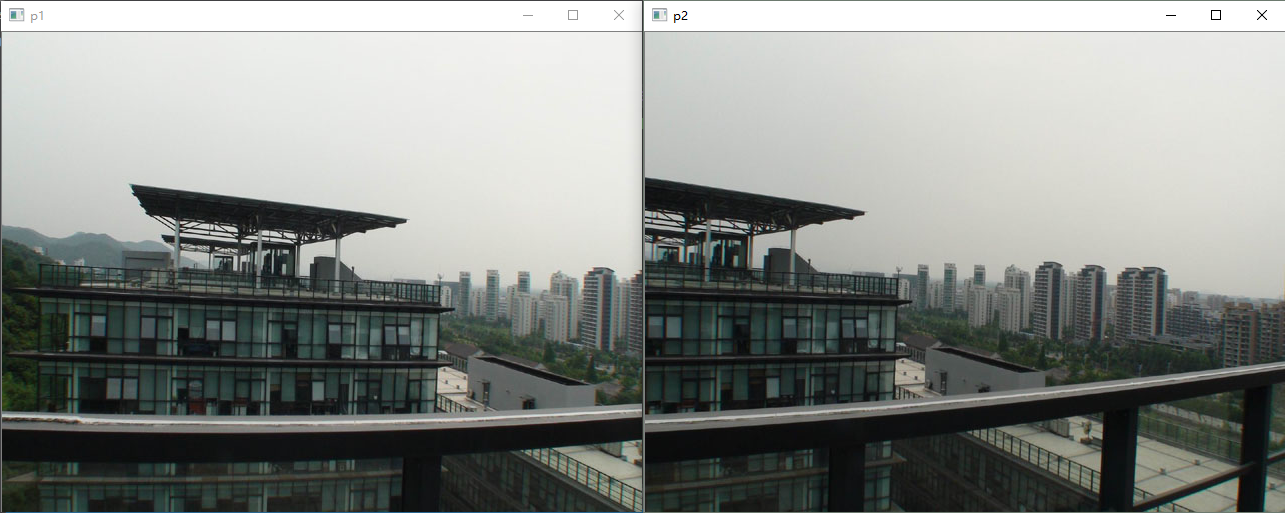
比如全景拼接 ：两张拍摄同一建筑的图像，人类能通过"相同的岩石拐角"对齐，但计算机需要找到这两个"角点"的坐标，才能将图像拼接成全景图。

1.3 角点的"特殊之处"

角点相比边缘、斑点等特征，有4个显著优势：

1. 局部性：属于"点特征"，对遮挡（比如物体被部分挡住）有鲁棒性；
2. 数量多：一张图像能检测出成百上千个角点，足够用于匹配；
3. 辨识度高：不同物体的角点差异明显，容易区分；
4. 速度快：提取过程计算量小，适合实时任务。

二、Harris角点检测：算法原理

Harris角点检测的核心思想是：通过窗口移动分析灰度变化------如果窗口向任意方向移动，灰度都发生显著变化，则窗口中心是角点。

2.1 灰度变化的数学描述

假设我们有一个大小为WWW的窗口，将其向(u,v)(u,v)(u,v)方向移动，窗口内的灰度变化可以用以下公式量化：

E(u,v)=∑(x,y)∈Ww(x,y)[I(x+u,y+v)−I(x,y)]2 E(u,v) = \sum_{(x,y) \in W} w(x,y) \left[ I(x+u, y+v) - I(x,y) \right]^2 E(u,v)=(x,y)∈W∑w(x,y)[I(x+u,y+v)−I(x,y)]2

参数解释：

• (u,v)(u,v)(u,v)：窗口的偏移量（比如向右移动2像素、向下移动3像素）；
• (x,y)(x,y)(x,y)：窗口内的像素坐标；
• I(x,y)I(x,y)I(x,y)：(x,y)(x,y)(x,y)处的灰度值；
• w(x,y)w(x,y)w(x,y)：窗口加权函数（通常用高斯函数，离窗口中心越近的像素权重越大）。

2.2 公式化简：泰勒展开的妙用

直接计算E(u,v)E(u,v)E(u,v)的计算量很大，我们可以用泰勒展开简化：

对于二维函数I(x+u,y+v)I(x+u, y+v)I(x+u,y+v)，泰勒展开近似为：I(x+u,y+v)≈I(x,y)+uIx+vIy I(x+u, y+v) \approx I(x,y) + u I_x + v I_y I(x+u,y+v)≈I(x,y)+uIx+vIy

其中，Ix=∂I∂xI_x = \frac{\partial I}{\partial x}Ix=∂x∂I（xxx方向梯度，反映水平方向的灰度变化），Iy=∂I∂yI_y = \frac{\partial I}{\partial y}Iy=∂y∂I（yyy方向梯度，反映垂直方向的灰度变化）。

将泰勒展开代入E(u,v)E(u,v)E(u,v)，化简后得到：E(u,v)≈[uv]M[uv] E(u,v) \approx \begin{bmatrix} u & v \end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix} E(u,v)≈[uv]M[uv]

其中，矩阵MMM是灰度变化的协方差矩阵 ，由梯度的加权和构成：M=[ABBC],A=∑w(x,y)Ix2,B=∑w(x,y)IxIy,C=∑w(x,y)Iy2 M = \begin{bmatrix} A & B \\ B & C \end{bmatrix}, \quad \begin{aligned} A &= \sum w(x,y) I_x^2, \\ B &= \sum w(x,y) I_x I_y, \\ C &= \sum w(x,y) I_y^2 \end{aligned} M=[ABBC],ABC=∑w(x,y)Ix2,=∑w(x,y)IxIy,=∑w(x,y)Iy2

2.3 角点的"判断标准"：响应函数RRR

矩阵MMM的特征值 （λ1,λ2\lambda_1, \lambda_2λ1,λ2）能反映窗口内的灰度变化特性：

• 平坦区域：λ1≈0,λ2≈0\lambda_1 \approx 0, \lambda_2 \approx 0λ1≈0,λ2≈0（灰度几乎不变）；
• 边缘区域：一个特征值很大，另一个很小（仅垂直边缘方向有变化）；
• 角点区域：两个特征值都很大（任意方向都有变化）。

为了量化这一特性，Harris提出了响应函数 RRR：R=det⁡(M)−k⋅trace(M)2 R = \det(M) - k \cdot \text{trace}(M)^2 R=det(M)−k⋅trace(M)2

其中：

• det⁡(M)=A⋅C−B2\det(M) = A \cdot C - B^2det(M)=A⋅C−B2（矩阵的行列式）；
• trace(M)=A+C\text{trace}(M) = A + Ctrace(M)=A+C（矩阵的迹）；
• kkk：经验常数（通常取0.04~0.06）。

2.4 算法流程总结

Harris角点检测的完整步骤：

1. 计算梯度 ：用Sobel算子计算图像的IxI_xIx和IyI_yIy；
2. 构建矩阵MMM ：计算Ix2,Iy2,IxIyI_x^2, I_y^2, I_x I_yIx2,Iy2,IxIy的高斯加权和，得到A,B,CA, B, CA,B,C；
3. 计算响应值RRR ：对每个像素计算RRR；
4. 阈值处理 ：保留R>thresholdR > \text{threshold}R>threshold的像素；
5. 非极大值抑制 ：在局部区域（比如3×3窗口）中保留RRR最大的像素，得到最终角点。

三、Python-OpenCV实现Harris角点检测

OpenCV提供了cv2.cornerHarris函数，可以快速实现Harris角点检测。以下是完整步骤：

3.1 准备工作：安装依赖

首先安装OpenCV和NumPy：

pip install opencv-python numpy matplotlib

3.2 OpenCV API实现

以下代码演示如何用cv2.cornerHarris检测角点：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 1. 读取图像（转为灰度图）
img = cv2.imread('test_image.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
gray = np.float32(gray)  # cornerHarris要求输入为float32

# 2. 计算Harris响应值
# 参数说明：
# - src：灰度图（float32）
# - blockSize：窗口大小（比如2表示2×2窗口）
# - ksize：Sobel算子的大小（比如3表示3×3 Sobel）
# - k：响应函数的系数（0.04~0.06）
harris_response = cv2.cornerHarris(gray, blockSize=2, ksize=3, k=0.04)

# 3. 阈值处理：保留响应值大的像素
# 将响应值放大（便于可视化），并标记角点为红色
harris_response = cv2.dilate(harris_response, None)
img[harris_response > 0.01 * harris_response.max()] = [0, 0, 255]  # 红色标记角点

# 4. 显示结果
plt.figure(figsize=(10, 8))
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
plt.title('Harris Corner Detection')
plt.axis('off')
plt.show()

3.3 手动实现：理解底层逻辑

为了更深入理解，我们可以手动实现Harris角点检测的核心步骤：

import cv2
import numpy as np
from scipy.ndimage import gaussian_filter
import matplotlib.pyplot as plt

def manual_harris(gray_img, block_size=2, k=0.04, sigma=1.0):
    # 1. 计算梯度（Sobel算子）
    grad_x = cv2.Sobel(gray_img, cv2.CV_64F, 1, 0, ksize=3)
    grad_y = cv2.Sobel(gray_img, cv2.CV_64F, 0, 1, ksize=3)

    # 2. 计算梯度的平方和乘积
    grad_x2 = gaussian_filter(grad_x**2, sigma=sigma)
    grad_y2 = gaussian_filter(grad_y**2, sigma=sigma)
    grad_xy = gaussian_filter(grad_x * grad_y, sigma=sigma)

    # 3. 计算响应值R
    det_M = grad_x2 * grad_y2 - grad_xy**2
    trace_M = grad_x2 + grad_y2
    R = det_M - k * (trace_M)**2

    # 4. 非极大值抑制（保留局部最大值）
    kernel = np.ones((block_size, block_size), np.uint8)
    local_max = cv2.dilate(R, kernel) == R
    R[~local_max] = 0

    return R

# 测试手动实现
gray = cv2.cvtColor(cv2.imread('test_image.jpg'), cv2.COLOR_BGR2GRAY)
R = manual_harris(gray)
# 阈值处理并显示
img = cv2.imread('test_image.jpg')
img[R > 0.01 * R.max()] = [0, 0, 255]
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
plt.show()

四、总结与扩展

Harris角点检测是计算机视觉中最经典的点特征提取算法，它的优势是计算速度快、对旋转和光照变化鲁棒，但也有局限性（比如对尺度变化不敏感）。

如果需要处理尺度变化的场景，可以学习SIFT （尺度不变特征变换）或ORB（更快的替代方案）。而Harris算法作为基础，是理解这些高级算法的关键。