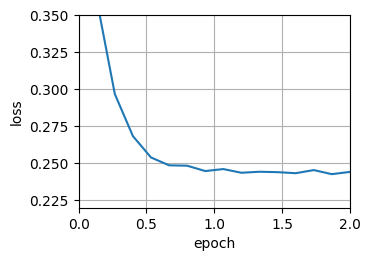
1.梯度下降算法

python
复制代码
%matplotlib inline
import numpy as np
import torch
from d2l import torch as d2l
##########################################################################
#绘图函数
def show_trace(results, f):
n = max(abs(min(results)), abs(max(results)))
f_line = torch.arange(-n, n, 0.01)
d2l.set_figsize()
d2l.plot([f_line, results], [[f(x) for x in f_line], [
f(x) for x in results]], 'x', 'f(x)', fmts=['-', '-o'])
# 目标函数
def f(x):
return x ** 2
# 目标函数的梯度(导数)
def f_grad(x):
return 2 * x
def gd(eta,f_grad):
x=10.0
results=[x]
for i in range(10):
x=x-eta*f_grad(x)
results.append(float(x))
print(f"epoch {i}:x={x:.5f}")
return results
##########################################################################
results=gd(0.2,f_grad)
show_trace(results, f)
##########################################################################
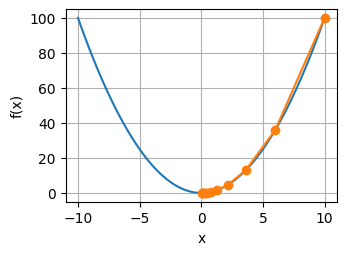
2.随机梯度下降算法

python
复制代码
%matplotlib inline
import numpy as np
import torch
from d2l import torch as d2l
def f(x1, x2): # 目标函数
return x1 ** 2 + 2 * x2 ** 2
def f_grad(x1, x2): # 目标函数的梯度
return 2 * x1, 4 * x2
def sgd(x1, x2, s1, s2, f_grad):
g1,g2=f_grad(x1,x2)
#模拟有噪声的梯度
g1 += np.random.normal(0.0, 1, (1,)).item()
g2 += np.random.normal(0.0, 1, (1,)).item()
#这里eta_t要进行更新,或者说叫衰减
eta_t = eta * lr
return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0)
eta=0.1
lr=0.9
d2l.show_trace_2d(f, d2l.train_2d(sgd, steps=50, f_grad=f_grad))
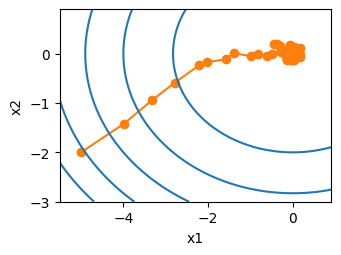
3.小批量随机梯度下降算法

python
复制代码
import numpy as np
import torch
from torch import nn
import matplotlib.pyplot as plt
from d2l import torch as d2l
np.random.seed(0)
torch.manual_seed(0)
#定义个线性回归网络
class LinearRegressionModel(torch.nn.Module):
def __init__(self):
super(LinearRegressionModel, self).__init__()
self.linear = torch.nn.Linear(1, 1)
def forward(self, x):
return self.linear(x)
#数据集生成
#100个样本
X = torch.randn(100, 1) * 10
y = 2 * X + 1 + torch.randn(100, 1) * 2
# 设置超参数
batch_size = 16
lr = 0.01
num_epochs = 100
model = LinearRegressionModel()
loss_fn = torch.nn.MSELoss()
dataset = torch.utils.data.TensorDataset(X, y)
data_loader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)
#训练:
losses = []
for epoch in range(num_epochs):
epoch_loss = 0.0
for i, (batch_X, batch_y) in enumerate(data_loader):
model.zero_grad()
predictions = model(batch_X)
loss = loss_fn(predictions, batch_y)
loss.backward()
#每一个batch都进行param的更新
with torch.no_grad():
for param in model.parameters():
param -= lr * param.grad
epoch_loss += loss.item()
avg_loss = epoch_loss / len(data_loader)
losses.append(avg_loss)
print(f"Epoch {epoch+1}/{num_epochs}, Loss: {avg_loss:.4f}")
#绘制对应图像
fig, axs = plt.subplots(1, 2, figsize=(12, 6))
axs[0].plot(range(1, num_epochs + 1), losses, label='Loss')
axs[0].set_xlabel('Epochs')
axs[0].set_ylabel('Loss')
axs[0].set_title('Training Loss')
axs[0].legend()
with torch.no_grad():
predicted = model(X).numpy()
axs[1].scatter(X.numpy(), y.numpy(), label='True Data')
axs[1].plot(X.numpy(), predicted, label='Fitted Line', color='r')
axs[1].set_xlabel('X')
axs[1].set_ylabel('y')
axs[1].legend()
axs[1].set_title('Model Prediction vs True Data')
plt.tight_layout()
plt.show()
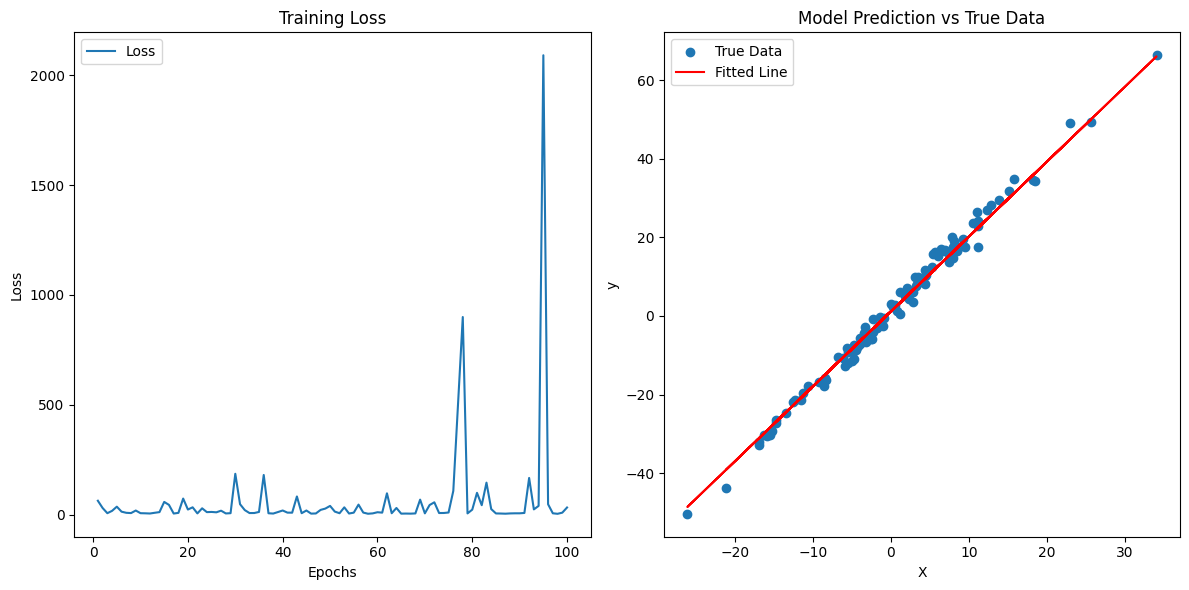
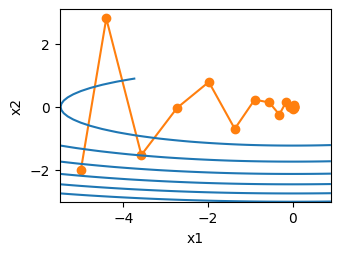
4.动量法


python
复制代码
#动量法
%matplotlib inline
import torch
from d2l import torch as d2l
eta = 0.4
def f_2d(x1, x2):
return 0.1 * x1 ** 2 + 2 * x2 ** 2
def momentum_2d(x1,x2,v1,v2):
v1=beta*v1+0.2*x1
v2=beta*v2+4*x2
return x1-eta*v1,x2-eta*v2,v1,v2
eta, beta = 0.6, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))
5.Adam

python
复制代码
%matplotlib inline
import torch
from d2l import torch as d2l
def init_adam_states(feature_dim):
v_w, v_b = torch.zeros((feature_dim, 1)), torch.zeros(1)
s_w, s_b = torch.zeros((feature_dim, 1)), torch.zeros(1)
return ((v_w, s_w), (v_b, s_b))
def adam(params, states, hyperparams):
beta1, beta2, eps = 0.9, 0.999, 1e-6
for p, (v, s) in zip(params, states):
with torch.no_grad():
#v_t=beta1*v_{t-1}+(1-beta1)*g_t
#s_t=beta2*s_{t-1}+(1-beta2)*g_t^2
v[:] = beta1 * v + (1 - beta1) * p.grad
s[:] = beta2 * s + (1 - beta2) * torch.square(p.grad)
#v_hat_t=v_t/(1-beta1^t)
#s_hat_t=s_t/(1-beta2^t)
v_bias_corr = v / (1 - beta1 ** hyperparams['t'])
s_bias_corr = s / (1 - beta2 ** hyperparams['t'])
#g'_t=eta*v_hat_t/((sqrt(s_hat_t)+epsion)
#x_t=x_t-1-g'_t
p[:] -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr)
+ eps)
p.grad.data.zero_()
hyperparams['t'] += 1
data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
d2l.train_ch11(adam, init_adam_states(feature_dim),
{'lr': 0.01, 't': 1}, data_iter, feature_dim)