自编码器与变分自编码器：【2】自编码器的局限性

引言：学习的本质是什么？

在人工智能的发展历程中，一个核心问题始终萦绕不去：机器如何学会理解数据的内在结构？ 人类能从几个像素识别一张脸，能从几个音符听出一段旋律，能从几个词语理解一段情感。这种从有限信息中理解整体的能力，正是表示学习的核心目标。

自编码器（Autoencoder）和变分自编码器（Variational Autoencoder）就是在这种背景下诞生的两种重要模型。它们不仅是深度学习中的重要组成部分，更是通往智能生成 和理解学习的关键桥梁。

自编码器与变分自编码器：从数据压缩到智能生成的进化 -- 【1】自编码器 - 数据压缩的艺术

一、代码示例

• 下面代码实现了一个简单的自编码器，用于对 FashionMNIST 数据集进行训练和可视化。
• 自编码器的结构包括一个编码器和解码器，能够将28x28 像素的图像压缩到 2 维潜在空间，以便进行可视化。
• 代码中包含了训练过程、潜在空间的可视化、重建图像的对比以及从随机潜在向量生成图像的功能。
• 通过观察潜在空间的分布和生成的图像，可以直观地理解自编码器的工作原理及其局限性。

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader

matplotlib.rcParams['axes.unicode_minus'] = False
matplotlib.rcParams['font.family'] = 'Kaiti SC'

# 设置随机种子确保可重现性
torch.manual_seed(42)
np.random.seed(42)

device = torch.device("mps" if torch.backends.mps.is_available() else "cuda" if torch.cuda.is_available() else "cpu")
print(f"使用设备: {device}")

# 数据预处理
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])

# 加载FashionMNIST数据集
train_dataset = torchvision.datasets.FashionMNIST(
    root='./data', train=True, download=True, transform=transform
)
test_dataset = torchvision.datasets.FashionMNIST(
    root='./data', train=False, download=True, transform=transform
)

batch_size = 512
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)

# 类别名称
class_names = ['T恤/上衣', '裤子', '套衫', '连衣裙', '外套',
               '凉鞋', '衬衫', '运动鞋', '包', '短靴']


class SimpleAutoencoder(nn.Module):
    """
    简单的自编码器，将图像压缩到2维以便可视化
    结构: 784 → 256 → 128 → 64 → 2 → 64 → 128 → 256 → 784
    """

    def __init__(self, latent_dim=2):
        super(SimpleAutoencoder, self).__init__()

        # 编码器
        self.encoder = nn.Sequential(
            nn.Linear(784, 256),
            nn.ReLU(True),
            nn.Linear(256, 128),
            nn.ReLU(True),
            nn.Linear(128, 64),
            nn.ReLU(True),
            nn.Linear(64, latent_dim)  # 2维潜在空间
        )

        # 解码器
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, 64),
            nn.ReLU(True),
            nn.Linear(64, 128),
            nn.ReLU(True),
            nn.Linear(128, 256),
            nn.ReLU(True),
            nn.Linear(256, 784),
            nn.Tanh()
        )

    def forward(self, x):
        x_flat = x.view(x.size(0), -1)
        encoded = self.encoder(x_flat)
        decoded = self.decoder(encoded)
        reconstructed = decoded.view(x.size(0), 1, 28, 28)
        return reconstructed, encoded


# 初始化模型
model = SimpleAutoencoder(latent_dim=2).to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)


# 训练函数
def train_autoencoder(model, train_loader, num_epochs=20):
    model.train()
    losses = []

    for epoch in range(num_epochs):
        epoch_loss = 0.0

        for batch_idx, (data, _) in enumerate(train_loader):
            data = data.to(device)

            # 前向传播
            reconstructed, _ = model(data)
            loss = criterion(reconstructed, data)

            # 反向传播
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            epoch_loss += loss.item()

        avg_loss = epoch_loss / len(train_loader)
        losses.append(avg_loss)
        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {avg_loss:.6f}')

    return losses


# 开始训练
print("开始训练自编码器...")
num_epochs = 10
train_losses = train_autoencoder(model, train_loader, num_epochs)
print("训练完成！")


# 可视化函数
def visualize_latent_space(model, data_loader, device, num_samples=1000):
    """可视化潜在空间"""
    model.eval()

    all_latents = []
    all_labels = []
    all_images = []

    with torch.no_grad():
        for i, (images, labels) in enumerate(data_loader):
            if len(all_latents) >= num_samples:
                break

            images = images.to(device)
            _, latents = model(images)

            all_latents.append(latents.cpu().numpy())
            all_labels.append(labels.numpy())
            all_images.append(images.cpu().numpy())

    # 合并数据
    latents_np = np.vstack(all_latents)[:num_samples]
    labels_np = np.concatenate(all_labels)[:num_samples]
    images_np = np.vstack(all_images)[:num_samples]

    return latents_np, labels_np, images_np


# 收集潜在表示
print("收集潜在表示...")
latents, labels, images = visualize_latent_space(model, test_loader, device, num_samples=2000)


# 绘制潜在空间分布
def plot_latent_space(latents, labels, class_names):
    """绘制潜在空间分布"""
    plt.figure(figsize=(10, 8))

    # 使用不同颜色和标记表示不同类别
    for i in range(10):
        idx = labels == i
        plt.scatter(latents[idx, 0], latents[idx, 1],
                    label=class_names[i], alpha=0.6, s=20)

    plt.xlabel('潜在维度 1')
    plt.ylabel('潜在维度 2')
    plt.title('自编码器潜在空间分布（2D）')
    plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
    plt.grid(True, alpha=0.3)

    # 添加潜在空间覆盖范围
    x_min, x_max = latents[:, 0].min(), latents[:, 0].max()
    y_min, y_max = latents[:, 1].min(), latents[:, 1].max()
    plt.xlim(x_min - 1, x_max + 1)
    plt.ylim(y_min - 1, y_max + 1)

    # 绘制潜在空间边界
    plt.axhline(y=0, color='gray', linestyle='--', alpha=0.3)
    plt.axvline(x=0, color='gray', linestyle='--', alpha=0.3)

    # 标记标准正态分布的范围
    std_normal_range = 3
    rect = plt.Rectangle((-std_normal_range, -std_normal_range),
                         2 * std_normal_range, 2 * std_normal_range,
                         fill=False, color='red', linestyle='--',
                         linewidth=2, label='标准正态分布范围 (±3σ)')
    plt.gca().add_patch(rect)

    plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
    plt.tight_layout()

    return plt.gca()


# 绘制潜在空间分布
print("绘制潜在空间分布...")
ax = plot_latent_space(latents, labels, class_names)
plt.show()


# 可视化重建结果对比
def visualize_reconstruction(model, data_loader, device, num_examples=10):
    """可视化原始图像和重建图像的对比"""
    model.eval()

    # 获取一批测试数据
    data_iter = iter(data_loader)
    images, labels = next(data_iter)
    images = images[:num_examples].to(device)
    labels = labels[:num_examples]

    with torch.no_grad():
        reconstructed, latents = model(images)

    # 将张量转换为numpy数组
    original_imgs = images.cpu().numpy()
    reconstructed_imgs = reconstructed.cpu().numpy()

    # 反归一化
    original_imgs = (original_imgs + 1) / 2
    reconstructed_imgs = (reconstructed_imgs + 1) / 2

    # 可视化对比
    fig, axes = plt.subplots(2, num_examples, figsize=(15, 4))

    for i in range(num_examples):
        # 原始图像
        axes[0, i].imshow(original_imgs[i, 0], cmap='gray')
        axes[0, i].set_title(f'原始\n{class_names[labels[i]]}', fontsize=10)
        axes[0, i].axis('off')

        # 重建图像
        axes[1, i].imshow(reconstructed_imgs[i, 0], cmap='gray')
        axes[1, i].set_title(f'重建\n({latents[i, 0]:.1f}, {latents[i, 1]:.1f})', fontsize=10)
        axes[1, i].axis('off')

    plt.suptitle('原始图像与重建图像对比（自编码器）', fontsize=16, y=1.05)
    plt.tight_layout()
    plt.show()

    return original_imgs, reconstructed_imgs, latents.cpu().numpy()


# 可视化重建对比
print("可视化重建对比...")
original, reconstructed, latent_points = visualize_reconstruction(model, test_loader, device)


# 从随机潜在向量生成图像
def generate_from_random_latent(model, num_samples=10, latent_range=(-3, 3)):
    """从随机潜在向量生成图像"""
    model.eval()

    with torch.no_grad():
        # 从均匀分布随机采样潜在向量
        z_random = torch.rand(num_samples, 2) * (latent_range[1] - latent_range[0]) + latent_range[0]
        z_random = z_random.to(device)

        # 生成图像
        generated = model.decoder(z_random)
        generated = generated.view(-1, 1, 28, 28)
        generated = generated.cpu().numpy()

        # 反归一化
        generated = (generated + 1) / 2
        generated = np.clip(generated, 0, 1)

        return generated, z_random.cpu().numpy()


# 可视化随机生成的结果
def visualize_random_generations(model, num_examples=20):
    """可视化从随机潜在向量生成的图像"""
    # 从不同范围采样
    ranges = [(-10, 10), (-5, 5), (-3, 3), (-1, 1)]
    range_labels = ['从[-10,10]采样', '从[-5,5]采样', '从[-3,3]采样', '从[-1,1]采样']

    fig, axes = plt.subplots(len(ranges), num_examples // len(ranges),
                             figsize=(15, 6))

    for i, (latent_range, range_label) in enumerate(zip(ranges, range_labels)):
        generated, z_values = generate_from_random_latent(
            model, num_examples // len(ranges), latent_range
        )

        for j in range(num_examples // len(ranges)):
            axes[i, j].imshow(generated[j, 0], cmap='gray')
            axes[i, j].axis('off')

            # 在左上角显示潜在向量
            axes[i, j].text(0.05, 0.95, f'({z_values[j, 0]:.1f}, {z_values[j, 1]:.1f})',
                            transform=axes[i, j].transAxes, fontsize=8,
                            verticalalignment='top', bbox=dict(boxstyle='round', facecolor='white', alpha=0.8))

    # 添加行标题
    for i, range_label in enumerate(range_labels):
        # 在图形坐标中添加行标题
        fig.text(0.02, 0.85 - i * 0.2, range_label, fontsize=12,
                 ha='left', va='center', rotation=0)

    plt.suptitle('从随机潜在向量生成的图像（自编码器）', fontsize=16, y=0.98)
    plt.tight_layout(rect=[0.05, 0, 1, 0.95])  # 调整布局，为左侧标题留出空间
    plt.show()

    return generated


# 可视化随机生成
print("可视化随机生成的图像...")
generated_images = visualize_random_generations(model, num_examples=20)

二、代码结果分析

2.1 潜在空间分布图

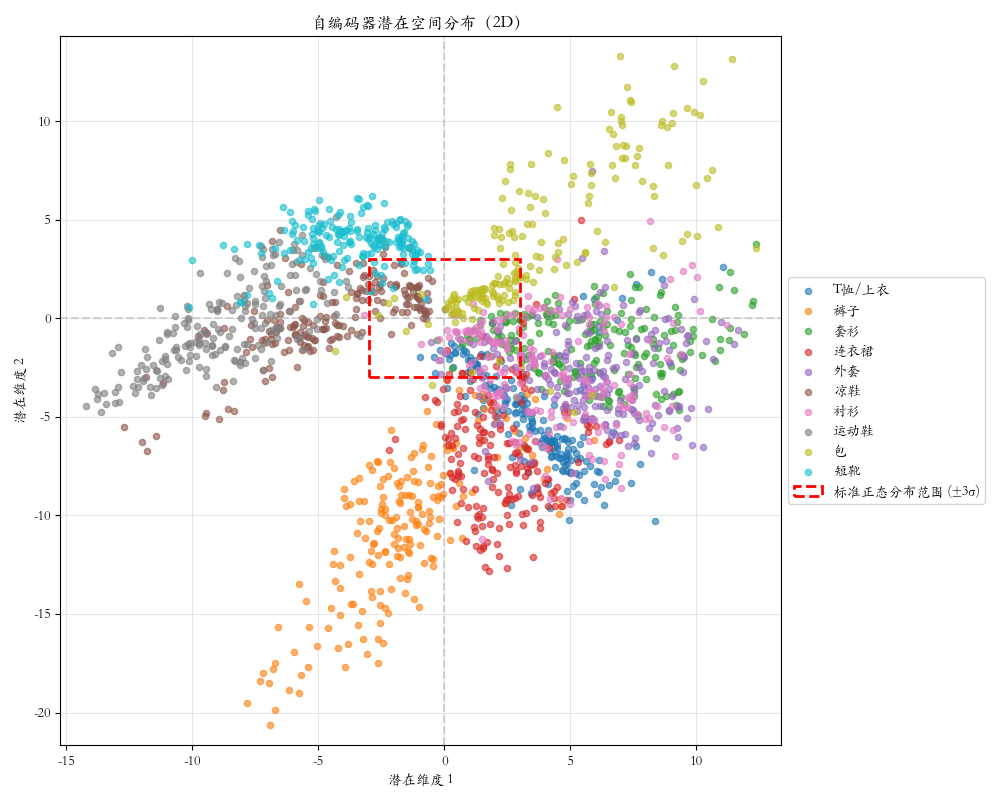
潜在空间的无序性：从图中可见，10类服装数据的潜在表示散布在横轴-15到10、纵轴-10到10的广阔范围内，远超红色虚线框标识的标准正态分布范围（±3σ）。

问题显现：

• 各类别点相互混杂，无清晰边界
• 存在空洞区域，空间不连续
• 潜在空间结构任意，无明确规律

启示：潜在空间缺乏先验约束，难以从已知分布中采样生成有效样本。

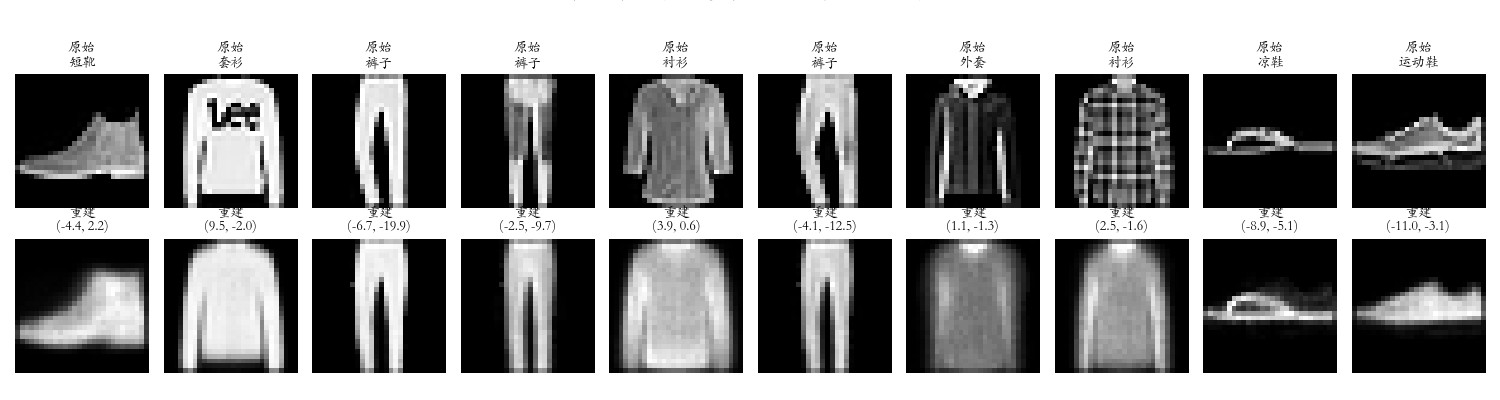
2.2 重建对比图

重建能力评估：图中对比了原始服装图像与自编码器重建结果，展示出自编码器的核心能力。

观察要点：

• 重建图像能保留类别特征，可辨识服装类型
• 但细节丢失，边界模糊，分辨率降低
• 图像质量明显低于原始，仅为近似表示

结论 ：自编码器学会了关键特征的压缩表示 ，但受限于信息瓶颈，无法完美重建细节。

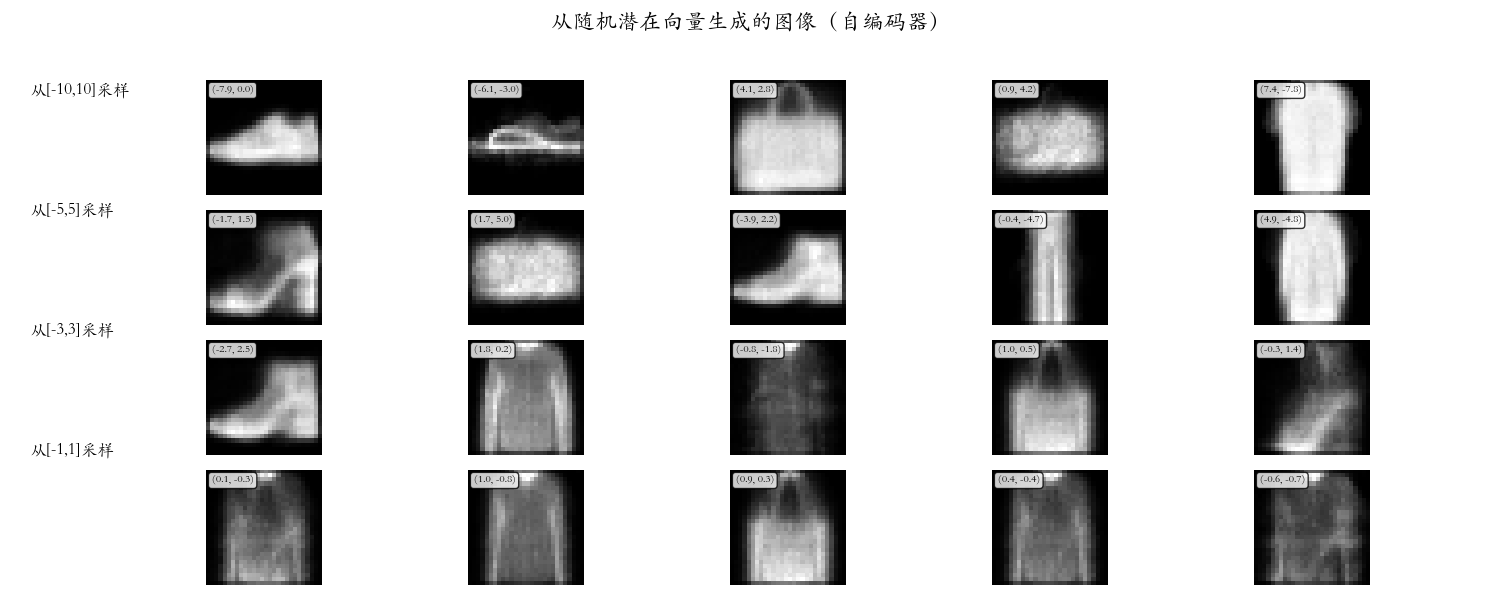
2.3 随机生成图

生成能力测试：从不同范围的潜在空间随机采样，测试自编码器的生成能力。

结果分析：

• 从[-10,10]采样：生成完全噪声
• 从[-3,3]采样：模糊轮廓，类别难辨
• 从[-1,1]采样：质量最好，但仍不清晰

关键发现：

1. 采样范围越小越好，说明训练数据集中潜在点相对集中
2. 重建质量 >> 生成质量
3. 解码器只认识训练见过的潜在点

核心局限 ：解码器是过拟合的映射函数 ，而非真正的生成模型。

三、自编码器的局限性分析

潜在空间无约束：

1. 训练目标仅最小化重建误差： L = ∥ x − x ′ ∥ 2 \mathcal{L} = \|\mathbf{x} - \mathbf{x'}\|^2 L=∥x−x′∥2
2. 对潜在变量 z \mathbf{z} z无任何约束
3. 潜在空间结构任意，难以进行有意义的采样

重建与生成的差距：

1. 重建过程 ： z = E ( x ) \mathbf{z} = E(\mathbf{x}) z=E(x)， x ′ = D ( z ) \mathbf{x}' = D(\mathbf{z}) x′=D(z)
   • 编码器 E E E提供训练见过的 z \mathbf{z} z
   • 解码器 D D D能够处理
2. 生成过程 ： z ∼ Uniform ( a , b ) \mathbf{z} \sim \text{Uniform}(a,b) z∼Uniform(a,b)， x ′ = D ( z ) \mathbf{x}' = D(\mathbf{z}) x′=D(z)
   • 随机采样 z \mathbf{z} z，解码器未见过
   • 解码器输出无意义结果

潜在空间空洞问题：

1. 随机采样 z \mathbf{z} z易落入空洞
2. 线性插值结果不稳定
3. 生成结果不可控

设训练数据潜在表示为集合 Z train \mathcal{Z}{\text{train}} Ztrain，则：
Z train ⊂ R 2 但 Z train ≠ R 2 \mathcal{Z}{\text{train}} \subset \mathbb{R}^2 \quad \text{但} \quad \mathcal{Z}_{\text{train}} \neq \mathbb{R}^2 Ztrain⊂R2但Ztrain=R2

存在大片空白区域 R 2 ∖ Z train \mathbb{R}^2 \setminus \mathcal{Z}_{\text{train}} R2∖Ztrain。

对于任意两个训练点 z 1 , z 2 ∈ Z train \mathbf{z}1, \mathbf{z}2 \in \mathcal{Z}{\text{train}} z1,z2∈Ztrain，线性插值：
z α = ( 1 − α ) z 1 + α z 2 , α ∈ [ 0 , 1 ] \mathbf{z}{\alpha} = (1-\alpha)\mathbf{z}_1 + \alpha\mathbf{z}_2, \quad \alpha \in [0,1] zα=(1−α)z1+αz2,α∈[0,1]

可能经过 z α ∉ Z train \mathbf{z}{\alpha} \notin \mathcal{Z}{\text{train}} zα∈/Ztrain，导致解码失败。